安全管理“事不过三”的数学原理

刘文生，易龙涛

（湖北工业大学 土木工程与建筑学院，湖北 武汉430068）

随着传统企业向现代企业的转型，安全管理在企业的整体管理活动中占据了越来越重要的地位［1］。工作时，一次小小的失误，人们都能理解和接受，但一而再、再而三地失误，就不能为人们所接受。领导的口头警告常常是:“事不过三、下不为例”［2］。“事不过三”是我们的生活总结，为什么不是“事不过四”或者“事不过五”呢？这里又有什么理论依据呢？

1 海因里希法则

美国人海因里希（W.H.Heinrich）对无伤害事件进行过较为深入的研究，他在调查了55万多起伤害事故后发现，每发生330起意外事件，有300件未产生人员伤害，29件造成人员轻伤，1件导致重伤或死亡，即重伤或死亡、轻伤和无伤害事件的比例为1∶29∶300。重伤和死亡事故虽然有偶然性，但是不安全因素或动作在事故发生之前就已暴露过许多次，如果在事故发生之前，抓住时机，及时消除不安全因素，许多重大伤亡事故是完全可以避免的。因此，重视无伤害事件可提高企业安全管理水平，达到预防和控制事故的目的。

每一起重大事故后面，必然存在无数“事故征兆”和“事故苗头”，也伴随着无数次无伤害事件的先期发生。海因里希法则反映了事故发生频率与事故严重度之间的一般规律，且说明事故严重程度取决于具体的机会因素，具有随机性［3－4］。

2 通过正态分布原理论证“事不过三”

虽然采取了预防安全事故发生的各种技术措施，但安全事故仍然在继续发生。这是因为安全事故虽然具有偶然性，但也有其内在的必然性。安全事故的发生符合正态分布，失误越多，发生事故的概率就越大。

一般来说，如果一个量是由许多微小的独立随机因素影响的结果，那么就可以认为这个量具有正态分布（见中心极限定理）［5］。其正态分布随机变量x的概率密度

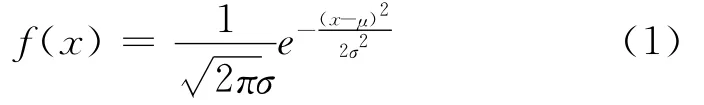
式中μ均数，σ标准差，可记作N（μ，σ）:

若x～N（u，σ2）时，P（｜x－μ｜≤σ）＝68.3%；P（｜x－μ｜≤2σ）＝95.4%；P（｜x－μ｜≤3σ）＝99.7%。在安全事故管理中，当事故发生的概率达到95.4%时，可认为是必然事件。依据海因里希的统计数据，当发生10.344（X＝300/29）次无伤害事件时，就必然会发生一起轻伤事故。因此，可简化计算，取μ＝0，σ＝10.344/2＝5.172，代入式（1）中计算概率密度f（x），计算结果见表1、图1。

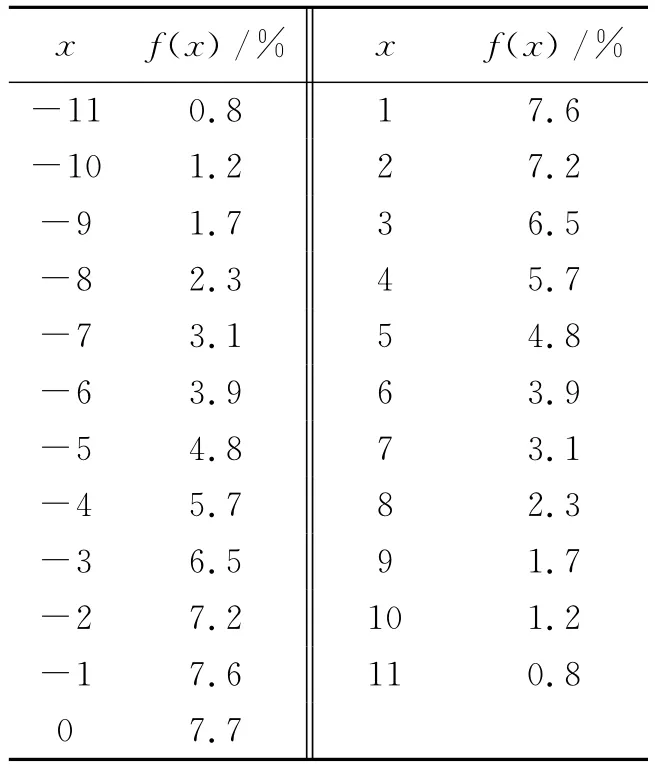
表1 轻伤概率密度计算

图1 轻伤概率密度分布图

发生安全事故概率函数为:

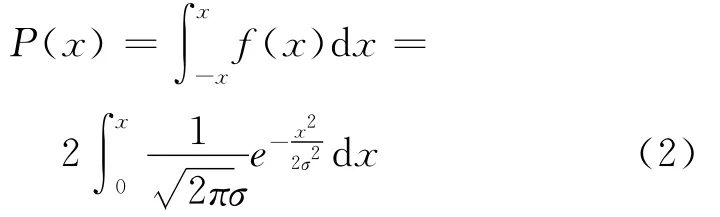
依式（2）计算对应概率见表2。

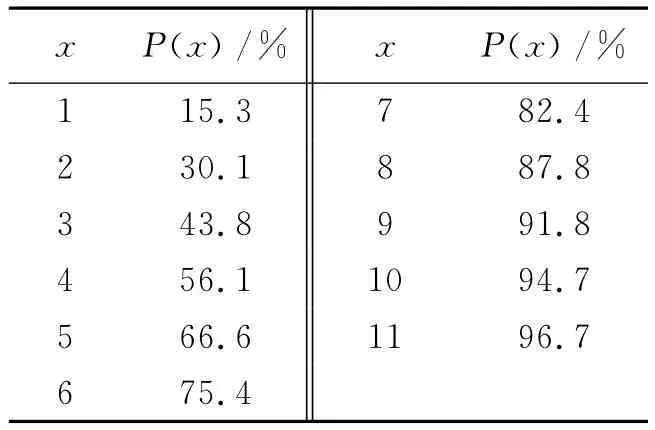
表2 发生轻伤事故概率计算

事故只有发生与不发生两种情况，从概率角度讲，他们各占50%。在安全事故管理中，事故发生的概率小于50%时，则认为发生的可能性小，事件处于相对安全状态；事故发生的概率超过50%时，则认为发生的可能性大，事件就认为处于不安全状态［6］。从表2可知，当事件发生次数达到3次时，发生伤害事故的概率为43.8%，还可认为处于一种相对安全状态；当事件发生次数达到4次时，发生伤害事故的概率为56.1%，这时的概率就已经很大了，事件就处于一种不安全状态，因此，第4次时就必须采取应对措施。这就是“事不过三”的基本原理。当然在极端状态下，第一次事件就有可能发生伤害甚至严重伤害。从大量的生产实践和统计发现，无伤害事件与轻伤事故之比为10.344∶1。

3 运用“事不过三”的数学原理对无伤害事件的控制

在安全事故管理中，如果不允许一次小小的失误，会导致人极度紧张，人在这种极度紧张的状态下工作，反而加剧了安全事故的发生。人在轻松或适度紧张的环境下工作，安全事故发生的概率最小。“事不过三”虽然来源于生活累积，但本文找到了其科学依据。“事不过三”是在第三次采取措施还是第四次采取措施？依据表2，应该在第三次事件发生之后采取措施，因为第四次的概率已经超出50%了。也就是说第三次失误发生之后，必须要采取措施改变生产环境和人的工作状态，使其向良性的方向改变。无伤害事件虽然没有造成人身伤害和经济损失，但由于其发生的原因和发展的过程与发生严重事故或重大事故是一致的，如果没有外力中断无伤害事件的发展趋势，极可能造成严重伤害或重大事故，因而，在发生第三次无伤害事件时必须进行预警控制，采取相应措施，消除事故原因或中断事故发展过程，达到控制和预防事故的目的。

当事故发生的概率达到90%以上时，风险极高，必须要阻止当前的生产环境和人的工作状态，由表2可知，第九次就极度危险了，离事故的发生只有一步之遥了。因此，在第八次事件发生时，必须拉响红色警报，停止当前行为。

依据黄、橙、红三级警报原则，事故发生的概率阀值分别对应为50%、70%、90%，事件发生的次数阀值分别为3、5、8［7－9］。第三次事件时，虽然拉响黄色警报，但第三次事件仍在安全范围内，目的是阻止第四次事件的发生。

在生产劳动过程中，每天都存在大量的失误。如果失误者不上报，这些失误也难以统计，最后仅仅成为茶余饭后的谈资。无伤害事件与有伤害事故相对比，其发生原因、发展过程是完全相同的。无伤害事件一般不会引起作业人员的重视，会产生侥幸心理和麻痹大意思想［10］。安全事故管理，责任重大，要让每一个劳动者重视“事不过三”的基本原理，并在生产劳动过程中加以运用。每一个人，对于自己的第三次失误，必须要主动自我警示和自我批评，找出原因，防止第四次失误。

4 重伤或死亡事故的控制

依据海因里希法则，重伤（或死亡）事故与轻伤事故之比为1:29。同上，在正态分布中的标准差为σ＝14.50。依据同样的方法通过轻伤次数x计算重伤（或死亡）的概率P（x）如表3。

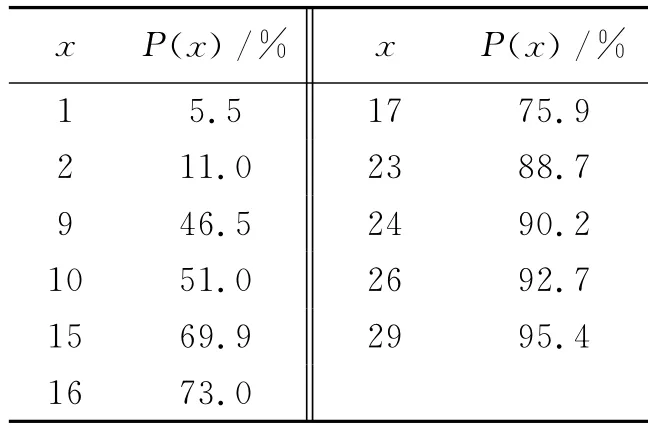
表3 发生重伤或死亡事故概率的计算

重伤或死亡黄、橙、红三级警报原则，事故发生的概率阀值仍然分别对应为50%、70%、90%，轻伤事故发生的次数阀值分别为9、15、23。即轻伤23次后，必须停工，并拉响红色警报。

［1］ 蒲小平.建筑施工企业安全管理问题与对策研究［D］.西安:长安大学，2012.

［2］ 冉 亮，冉艳平.浅析 “事不过三”［J］.科技信息，2011，18:451.

［3］ 卿玉国，赵国武，朱学安.安全管理骨牌理论和概率论的应用分析［J］.山东冶金，2008，30（01）:70-71.

［4］ 游鹏飞，寇玮华.浅析墨菲定律及海因里希法则对控制事故的作用［J］.安全.健康和环境，2009，8（08）:14-15.

［5］ 赵鹏毅，高 丽.正态分布在工程质量管理中的应用［J］.河北建筑科技学院学报，2002，19（02）:60-62.

［6］ 王福和.论管理中的小概率事件［J］.辽宁工程技术大学学报:社会科学版，2005，6（06）:636-637.

［7］ Grezio A，Marzocchi W，Sandri L，et al.A Bayesian procedure for probabilistic tsunami hazard assessment［J］.Natural hazards，2010，53（01）:159-174.

［8］ Dargahi-Noubary G R.Application of the threshold method to air quality data［J］.Natural Hazards，1988，1（03）:227-233.

［9］ Borch K.Probabilities of probabilities［J］.Theory and Decision，1975，6（02）:155-159.

［10］赵元庆，侯得恒.建筑施工项目安全预警系统的仿真研究［J］.计算机仿真，2013，30（02）:359-363.