Adaptive detection in the presence of signal mismatch

Weijian Liu,Wenchong Xie,Rongfeng Li,Fei Gao,Xiaoqin Hu,and Yongliang Wang,*

1.College of Electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China;

2.Air Force Early Warning Academy,Wuhan 430019,China

Adaptive detection in the presence of signal mismatch

Weijian Liu1,2,Wenchong Xie2,Rongfeng Li2,Fei Gao2,Xiaoqin Hu2,and Yongliang Wang2,*

1.College of Electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China;

2.Air Force Early Warning Academy,Wuhan 430019,China

The problem of adaptive detection in the situation of signal mismatch is considered;that is,the actual signal steering vector is not aligned with the nominal one.Two novel tunable detectors are proposed.They can control the degree to which the mismatched signals are rejected.Remarkably,it is found that they both cover existing famous detectors as their special cases.More importantly,they possess the constant false alarm rate(CFAR) property and achieve enhanced mismatched signal rejection or improved robustness than their natural competitors.Besides,they can provide slightly better matched signals detection performance than the existing detectors.

mismatched signal detection,adaptive coherence estimator(ACE),adaptive matched flter(AMF),generalized likelihood ratio test(GLRT),tunable detector.

1.Introduction

Adaptive detection of a signal embedded in Gaussian or non-Gaussian disturbance with unknown spectral properties has been an active research feld in the last three decades.A large number of approaches have been proposed in different situations[1–11].The most prominent and pioneering detection approaches are Kelly’s generalized likelihood ratio test(KGLRT)[1],the adaptive matched flter(AMF)[2],and the adaptive coherence estimator(ACE)[3].However,the above detectors have been designed without taking possible mismatched signals into account,and they behave quite differently in this situation.In practice,mismatched signals may arise due to multipath propagation,array calibration uncertainties,pointing errors,and so on.

A method to design robust detectors is modelling the signal as a vector belonging to a proper cone or assuming that the angle of the signal is partially or totally uncertain[12].The corresponding detectors can provide performance improvement in terms of target sensitivity (less tolerant to signal mismatch),but at the price of poor mismatched signal rejection.Another approach is modifying the hypothesis test by adding a fctitious signal only under the null hypothesis.This fctitious signal is assumed to be orthogonal to the prescribed one in whitened or quasi-whitened space.When there is no target in the presumed direction but one in another direction,the detector will choose the null hypothesis.This is the rationale of the adaptive beamformer orthogonal rejection test (ABORT)[13]and the whitened ABORT(W-ABORT) [14].They can achieve improved mismatched signal rejection,but have poor robustness to slightly mismatched signals.In[15,16],the authors assume that a constrained noise-like interference exists only in the cell under test (CUT),and the double-normalized AMF(DN-AMF)is proposed therein.The DN-AMF has enhanced mismatched signal rejection ability than that of the W-ABORT,however,it still exhibits poor robustness to slightly mismatched signals.

All the detectors mentioned above have the following common features.They either exhibit enhanced mismatched signal rejection or have more robustness to mismatched signals.Hence,it seems diffcult to fnd a decision scheme capable of effectively rejecting seriously mismatched signals(such as sidelobe targets)and successfully detecting slightly mismatched signals(for example, mainlobe targets)simultaneously.To cope with this limitation,the two-stage detectors[17–19]and tunable detectors[20–23]are proposed in the literature.The twostage detectors[17–19]are formed by cascading two detectors with converse capabilities of mismatched signal rejection.The presence of the target is declared only when data survive both detection thresholds.However,the capabilities of rejection and robustness to mismatched signals of these detectors are confned by these capabilities of their individual detectors.In contrast,the tunable detectors[20–22]can control the level to which the mismatched signals are rejected or detected,by tuning a scalar parameter.How-ever,the tunable detector in[20]has limited capabilities of mismatched signal rejection,while those in[21]and[22] are not robust to slightly mismatched signals.The twoparameter tunable detector in[23]has more fexibility of controlling the degree to which the mismatched signal is rejected.However,the manner how to choose a reasonable parameter pair does not seem easy.

In this paper,by investigating and comparing KGLRT, AMF,and ACE,we introduce two novel single-parameter tunable detectors,which are controlled by two positive tunable parameters.Both of them have simple structure but are very effective for detecting the mismatched signals.Moreover,they both embrace two well-known detectors as their special cases.An important feature of the novel tunable detectors is that they can provide better robustness than those in[21]and[22],and can achieve enhanced mismatched signal rejection than that in[20].Moreover,for matched signals,when the signal-to-clutter-plus-noise ratio(SCNR) is high enough,they can provide probabilities of detection (PDs),which are higher than those of the KGLRT,AMF, and ACE.

2.Problem formulation and design issues

Assume that the data are received by N sensors.Denote the data in the CUT by an N×1 vector x.We want to test if there exists a useful signal s0in x.The detection problem can be formulated in the following binary hypothesis test:

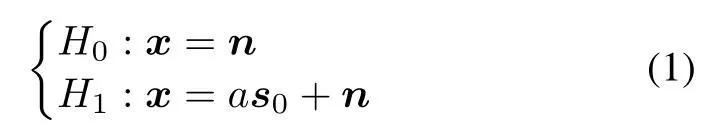
where n is the disturbance,containing clutter and white noise,which is modeled as a zero-mean complex circular Gaussian vector with covariance matrix E[nnH]=R.a is the signal amplitude and s0is the actual signal steering vector,which is not necessarily aligned with the nominal steering vector s.Note that R and a are both unknown.As customary,we assume that a set of training data,xl(l=1,2,...,L),are available;they are independent and identically distributed(i.i.d.),contain no signal, and share the same covariance matrix with the disturbance in the CUT,i.e.,It follows that the matrix S=XXHis L times the sample covariance matrix (SCM),with X=[x1,x2,...,xL]being the sample data matrix.

For the problem shown in(1),AMF[2],KGLRT[1], and ACE[3]are given by

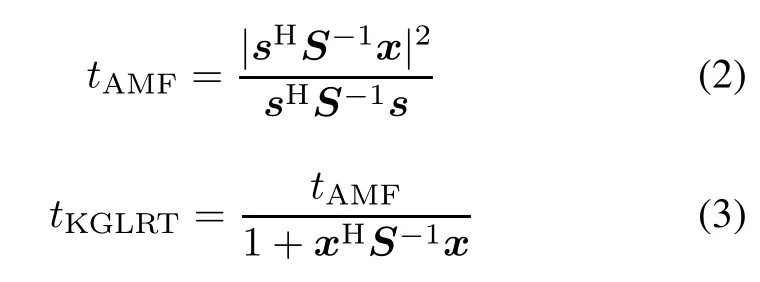
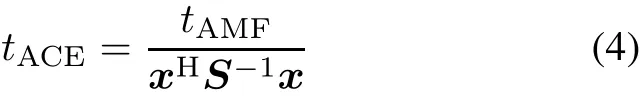
respectively.When a detector is statistically equivalent to another one,they share the same detection performance [24].Statistically equivalent detectors are usually related by monotonically increasing functions.Note that a statistically equivalent form of the KGLRT is[1]

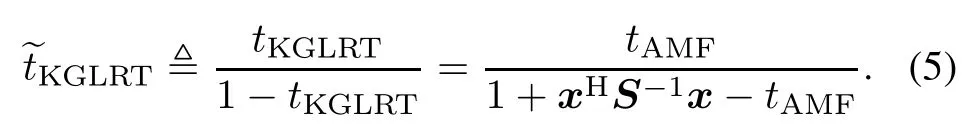
Analogously,we fnd that a statistically equivalent form of the ACE is

which is referred to as the adaptive cotangent detector (ACD)in this paper.The detectors in(4)and(6)are statistically equivalent to each other due to the fact that tACE=tACD/(1+tACD)can be taken as a monotonically increasing function of tACD.Furthermore,(6)can be recast as

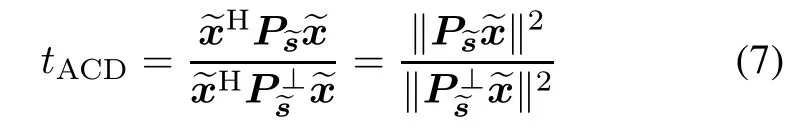
It is noteworthy that there exists certain similarity between AMF,KGLRT,and ACE.KGLRT and ACE are two different normalized versions of the AMF.Precisely, the normalization for the KGLRT is performed by(1+ xHS−1x)(for(3))or(1+xHS−1x−tAMF)(for(5)), while for the ACE this is done by xHS−1x.Moreover, from a mathematical viewpoint,(5)bears a resemblance to (6)in the sense that(5)and(6)share the identical numerator and same term xHS−1x−tAMFin the denominator.

Inspired by the analysis above,we introduce the following two novel tunable detectors:

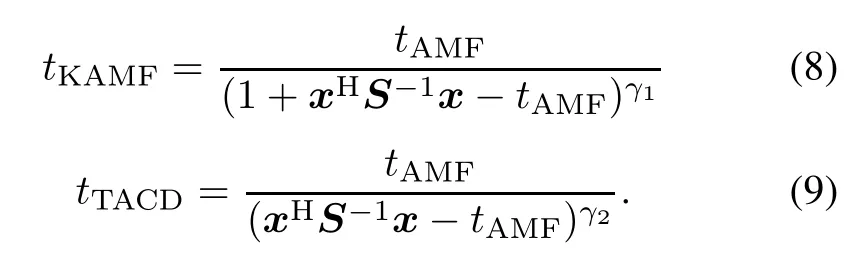
The quantities γ1and γ2are referred to as the tunable parameters,which play a key role in governing the level to which the mismatched signals are rejected.

Notice that,if γ1=0,(8)coincides with the AMF, while γ1=1,(8)is equivalent to the KGLRT.Moreover, when γ2=0,(9)is equal to the AMF,and when γ2=1, (9)becomes(6).In other words,when γ2=0,(9)is statistically equivalent to the ACE.

On the basis of the analysis above,we would like to name the tunable detector in(8)as the Kelly-AMF (KAMF)and name that in(9)as the tunable ACD(TACD).

3.Performance assessment

Closed-form expressions for probabilities of false alarm (PFAs)and PDs of KAMF and TACD are derived in this section.The equivalent form of the KGLRT shown in(5) can be recast as

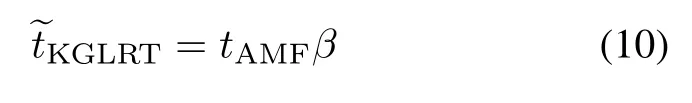
where

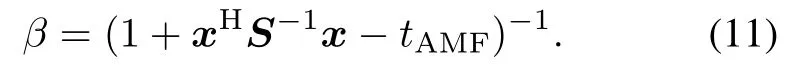
After some algebraic manipulations,we have the following two statistically equivalent forms of KAMF and TACD,given by

It is shown in[25]that,?tKGLRT,conditioned on β under the hypothesis H1is ruled by a complex noncentral F-distribution with 1 and L−N+1 degrees of freedom (DOFs)and a noncentrality parameter ρφ= βρcos2φ, where ρ=|a2|sH0R−1s0is defned as the output SCNR and

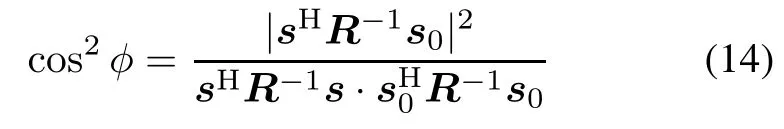
is the squared cosine of the array steering s and the actual signature s0in the whitened space.

Moreover,under the hypothesis H1,β is distributed as a complex noncentral Beta distribution with L−N+2 and N −1 DOFs and a noncentrality parameter δ2= ρ·sin2φs0,s[25].

Hence,the PDs of KAMF and TACD can be calculated as

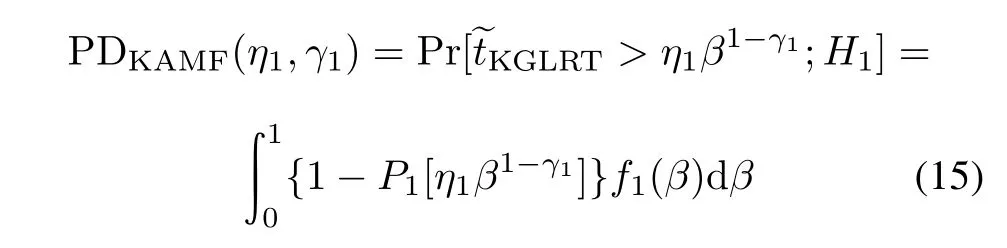
and

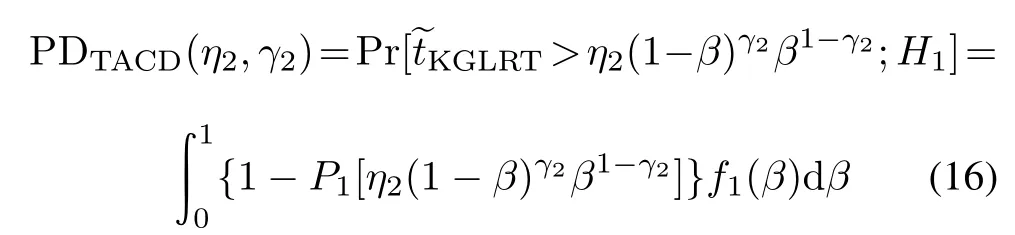
respectively,where η1and η2are the corresponding detection thresholds and P1(·)is the cumulative distribution function(CDF)of?tKGLRTwith β fxed.Precisely,P1(·)is given by[1]

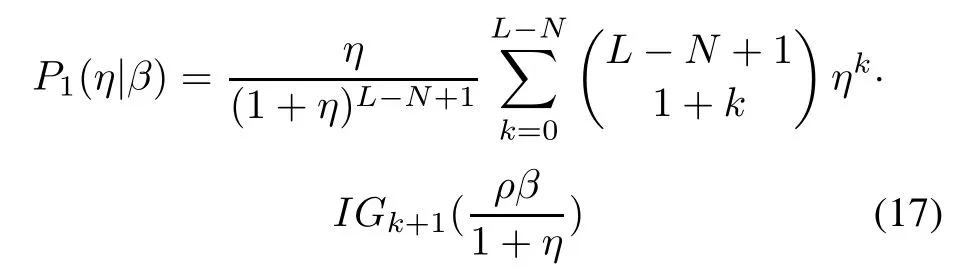
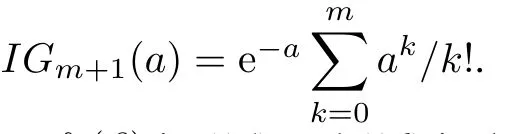
The term f1(β)in(15)and(16)is the probability density function(PDF)of β under the hypothesis H1.One form is found to be[25]

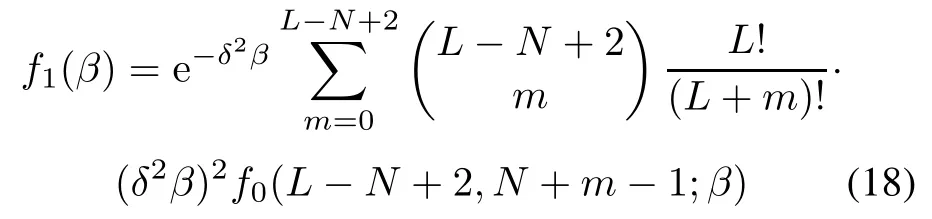
where f0(m,n;β)is the PDF of the complex central Beta distribution with m and n DOFs,described as[1]

where B(m,n)is the Beta function[26].

Setting the values of ρ and δ2to be zeros in(17)and (18),we obtain the CDF of?tKGLRTand the PDF of β under the hypothesis H0.Hence,the PFAs of KAMF and TACD can be computed as

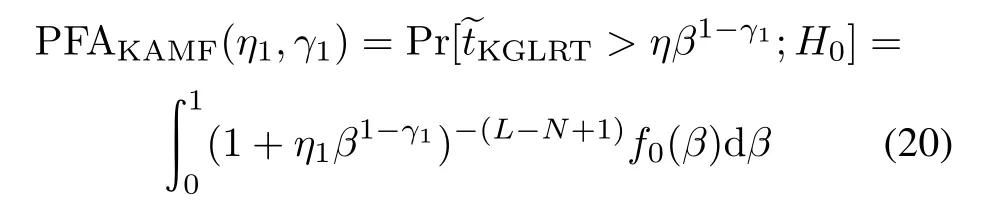
and

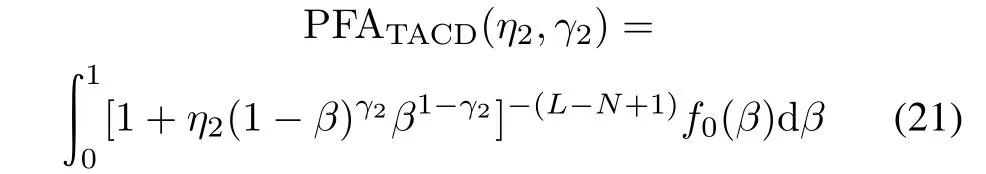
respectively,where we have used the identity 1−P0(x)= (1+x)−(L−N+1)[21],with P0(·)being the CDF of ?tKGLRTunder the hypothesis H0for given β.Clearly from (20)and(21),the PFAs are not dependent on R.Hence, KAMF and TACD both possess the constant false alarm rate(CFAR)property with respect to the noise covariance matrix R.

4.Numerical examples

This section is to verify the theoretical results derived above and to compare the proposed KAMF and TACD with the existing detectors.The numbers of sensors and training data are set to be N=24 and L=2N,respectively.The PFA is chosen as 10−4.

Fig.1 shows the PDs of KAMF and TACD with different tunable parameters.Four points can be inferred fromFig.1.First,both KAMF and TACD,with proper tunable parameters,can provide higher PDs than those of KGLRT, AMF,and ACE.Second,when the tunable parameters, i.e.,γ1and γ2,increase from zero to a certain value,the PDs of KAMF and TACD increase too.However,when the tunable parameters continue to increase,the PDs decrease.Third,with the increase of the tunable parameters, the downtrend of PD of the TACD is more rapid than that of the KAMF.Fourth,the curves,shown in Fig.1,verify the fact that when γ1=γ2=0,KAMF and TACD reduce to the AMF,while when γ1=1 the KAMF collapses to the KGLRT.Moreover,when γ2=1,the TACD degenerates into the ACE.

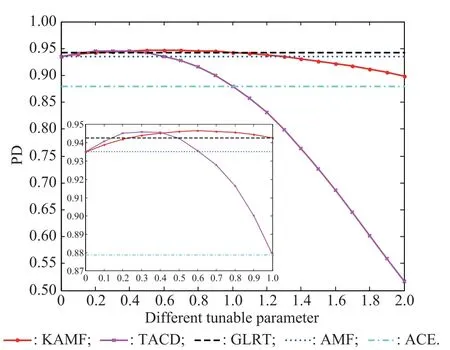
Fig.1 PDs of KAMF and TACD for the matched signals versus tunable parameters

The detection performance of KAMF and TACD for matched signals is characterized in a different manner in Fig.2,which displays the PD versus SCNR,also in comparison with KGLRT,AMF,and ACE.The tunable parameters are chosen as γ1=γ2=0.4.For independent confrmation,we also show the PDs obtained by Monte Carlo trials.In order to evaluate the PDs and the thresholds necessary to ensure a prescribed PFA,we resort to 2×104and 200/PFA independent data realizations,respectively.The symbol?represents the empirical PD of the TACD,and the symbol°stands for the empirical PD of KAMF.It is shown that the Monte Carlo simulations coincide with the analytical results quite well.Moreover,the results also indicate that KAMF and TACD exhibit detection performance comparable to that of the KGLRT.More precisely, when the SCNR is low or moderate,the PDs of KAMF and TACD are slightly lower than that of the KGLRT.In contrast,when the SCNR is high enough(such as SCNR＞16 dB),the PDs of KAMF and TACD are both slightly higher than that of the KGLRT.Notice that the PDs of KAMF and TACD are higher than those of AMF and ACE in the interval from 6 dB to 18 dB.

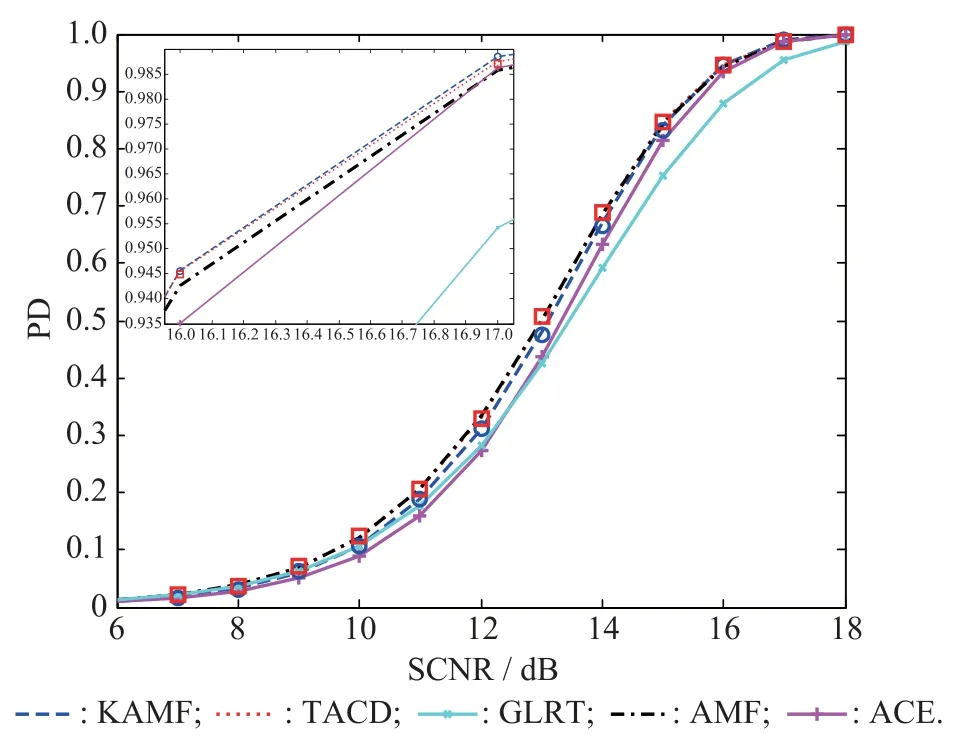
Fig.2 PDs of KAMF and TACD for matched signals versus SCNR

Before proceeding further,we would like to point out that although the possibility of the signal mismatch is not being taken into account at the stage of detector design,it is found that among the three prominent detectors,the AMF is the most robust,while the ACE is the most selective, and the KGLRT is in between[13,27].Figs.3 and 4 deal with the detection performance for the mismatched signal detection.More precisely,Fig.3 depicts the contours of the constant PDs under different SCNR and cos2φ.Such plots were frst introduced in[13],where they were named as the mesh-plots.The tunable parameters are set to be γ1=γ2=2 in Fig.3.As the capability of mismatched signal rejection of the KGLRT is between AMF and ACE, it is not reported in Fig.3.The results highlight that when the tunable parameters are selected properly,TACD and KAMF can exhibit enhanced mismatched signal rejection, compared to AMF and ACE.Moreover,the TACD has thebest capability of mismatched signal rejection,while the AMF has the least mismatch discrimination capabilities.

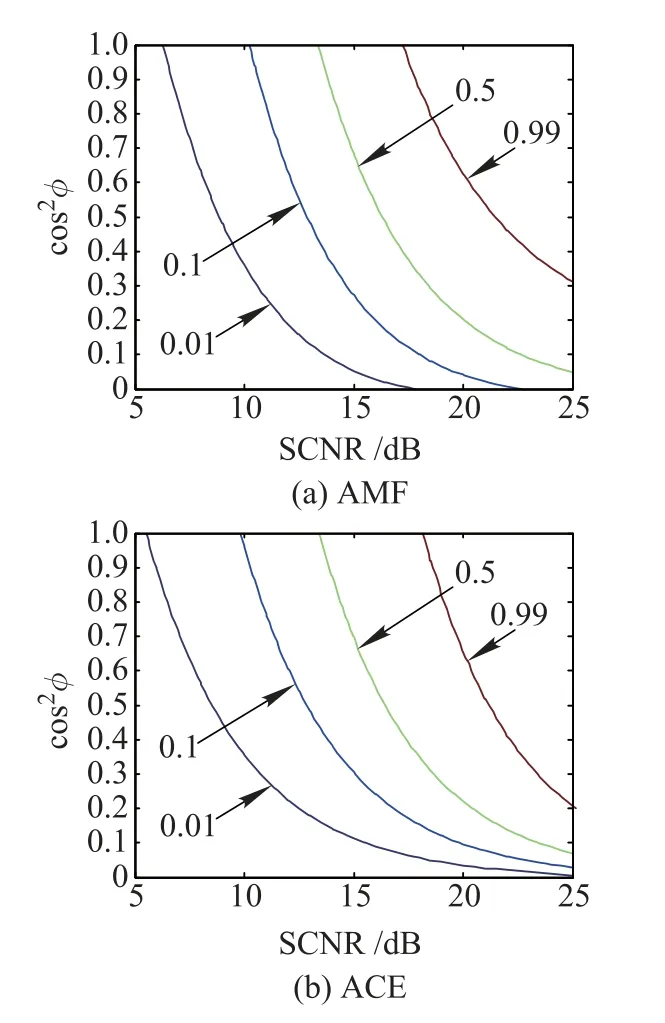
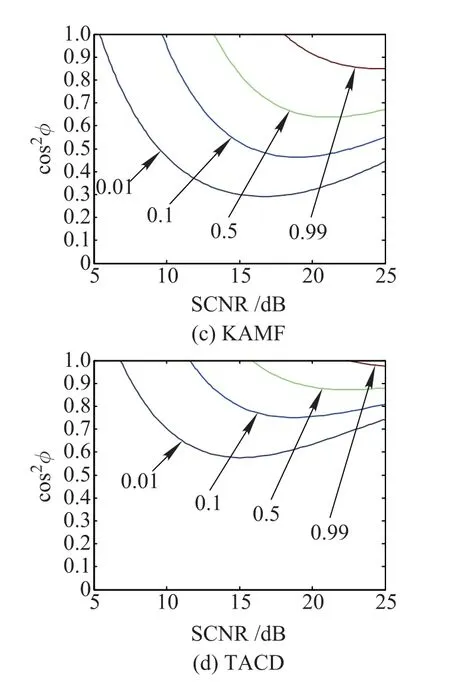
Fig.3 Contours of constant PDs for AMF,ACE,KAMF and TACD

Fig.4 illustrates the detection performance of the detectors under different cos2φ.Note that Fig.4 is a slice of Fig.3.When γ1=γ2=0,both KAMF and TACD reduce to the AMF,which is the most robust to the signal mismatch.In contrast,when γ1=γ2=2,they both exhibit enhanced mismatched signal rejection than KGLRT,AMF, and ACE.In fact,when γ2＞1,the TACD always has a stronger capability of mismatched signal rejection than that of the ACE.

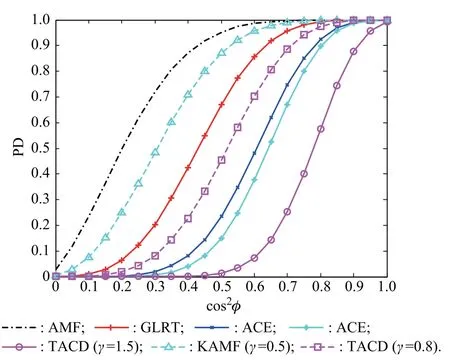
Fig.4 PDs of the detectors versus cos2φ(SCNR=20 dB)

5.Conclusions

In this paper,we have considered the problem of adaptive detection in the presence of signal mismatch.Two novel tunable detectors,namely,KAMF and TACD,have been introduced.The KAMF embraces KGLRT and AMF as its two special cases,while the TACD covers ACE and AMF as its two special cases.Compared to their natural counterparts,they both have higher PDs for matched signals and enhanced mismatched signal rejection.As for the selection of the tunable parameters,a general criterion is that if we want the detectors to possess the robustness to the signal mismatch,the tunable parameters should be set small enough[28].One example is that the radar operates in the searching pattern.In contrast,when we want the detectors to be selective to the signal mismatch,the tunable parameters should be chosen moderately large.One example is that the radar works in the tracking pattern.

[1]E.J.Kelly.An adaptive detection algorithm.IEEE Trans.on Aerospace and Electronic Systems,1986,22(1):115–127.

[2]F.C.Robey,D.R.Fuhrmann,E.J.Kelly,et al.A CFAR adaptive matched flter detector.IEEE Trans.on Aerospace and Electronic Systems,1992,28(1):208–216.

[3]S.Kraut,L.L.Scharf.The CFAR adaptive subspace detector is a scale-invariant GLRT.IEEE Trans.on Signal Processing, 1999,47(9):2538–2541.

[4]W.J.Liu,W.C.Xie,Y.L.Wang.Adaptive detection based on orthogonal partition of the primary and secondary data.Journal of Systems Engineering and Electronics,2014,25(1):34–42.

[5]W.J.Liu,W.C.Xie,J.Liu,et al.Adaptive double subspace signal detection in Gaussian background—part I:homogeneous environments.IEEE Trans.on Signal Processing,2014, 62(9):2345–2357.

[6]C.Hao,D.Orlando,G.Foglia,et al.Persymmetric adaptive detection of distributed targets in partially-homogeneous environment.Digital Signal Processing,2014,24:42–51.

[7]J.Liu,Z.J.Zhang,Y.Yang,et al.A CFAR adaptive subspace detector for frst-order or second-order Gaussian signals based on a single observation.IEEE Trans.on Signal Processing, 2011,59(11):5126–5140.

[8]J.Liu,Z.J.Zhang,P.L.Shui,et al.Exact performance analysis of an adaptive subspace detector.IEEE Trans.on Signal Processing,2012,60(9):4945–4950.

[9]G.Cui,A.de Maio,M.Piezzo.Performance prediction of the incoherent radar detector for correlated generalized Swerling-Chi fuctuating targets.IEEE Trans.on Aerospace and Electronic Systems,2013,49(1):356–368.

[10]L.Huang,H.C.So,C.Qian.Volume-based method for spectrum sensing.Digital Signal Processing,2014,28:48–56.

[11]J.Xu,J.Yu,Y.N.Peng,et al.Radon-fourier transform for radar target detection–Part I:Generalized Doppler flter bank.IEEE Trans.on Aerospace and Electronic Systems, 2011,47(2):1186–1202.

[12]A.de Maio.Robust adaptive radar detection in the presence of steering vector mismatches.IEEE Trans.on Aerospace and Electronic Systems,2005,41(4):1322–1337.

[13]N.B.Pulsone,C.M.Rader.Adaptive beamformer orthogonal rejection test.IEEE Trans.on Signal Processing,2001,49(3): 521–529.

[14]F.Bandiera,O.Besson,G.Ricci.An ABORT-like detector with improved mismatched signals rejection capabilities.IEEE Trans.on Signal Processing,2008,56(1):14–25.

[15]D.Orlando,G.Ricci.A Rao test with enhanced selectivity properties in homogeneous scenarios.IEEE Trans.on Signal Processing,2010,58(10):5385–5390.

[16]W.Liu,W.Xie,Y.Wang.A Wald test with enhanced selectivity properties in homogeneous environments.EURASIP Journal on Advances in Signal Processing,2013,DOI: 10.1186/1687–6180–2013–14.

[17]C.D.Richmond.Performance of the adaptive sidelobe blanker detection algorithm in homogeneous environments.IEEE Trans.on Signal Processing,2000,48(5):1235–1247.

[18]F.Bandiera,D.Orlando,G.Ricci.A subspace-based adaptive sidelobe blanker.IEEE Trans.on Signal Processing,2008, 56(9):4141–4151.

[19]C.Hao,B.Liu,L.Cai.Performance analysis of a two-stage Rao detector.Signal Processing,2011,91(8):2141–2146.

[20]S.Z.Kalson.An adaptive array detector with mismatched signal rejection.IEEE Trans.on Aerospace and Electronic Systems,1992,28(1):195–207.

[21]F.Bandiera,D.Orlando,G.Ricci.One-and two-stage tunable receivers.IEEE Trans.on Signal Processing,2009,57(8): 3264–3273.

[22]C.Hao,B.Liu,S.Yan,et al.Parametric adaptive radar detector with enhanced mismatched signals rejection capabilities.EURASIP Journal on Advances in Signal Processing, 2010,DOI:10.1155/2010/375136.

[23]W.Liu,W.Xie,J.Liu,et al.Detection of a distributed target with direction uncertainty.IET Radar,Sonar and Navigation, 2014,DOI:10.1049/iet-rsn.2014.0110.

[24]A.de Maio,S.M.Kay,A.Farina.On the invariance,coincidence,and statistical equivalence of the GLRT,Rao test, and Wald test.IEEE Trans.on Signal Processing,2010,58(4): 1967–1979.

[25]E.J.Kelly,K.M.Forsythe.Adaptive detection and parameter estimation for multidimensional signal models.Lexington: Lincoln Laboratory,1989.

[26]A.M.Mathai,H.J.Haubold.Special functions for applied scientists.Montreal:Springer,2008.

[27]A.de Maio.Rao test for adaptive detection in Gaussian interference with unknown covariance matrix.IEEE Trans.on Signal Processing,2007,55(7):3577–3584.

[28]W.J.Liu,W.C.Xie,Y.L.Wang.Parametric detector in the situation of mismatched signals.IET Radar,Sonar and Navigation,2014,8(1):48–53.

Biographies

Weijian Liu was born in 1982.He received his B.S.and M.S.degrees from Air Force Radar Academy,Wuhan,China,in 2006 and 2009,respectively.He is currently working toward his Ph.D.degree at National University of Defense Technology,Changsha,China.His current research interests include multichannel signal detection,statistical and array signal processing.

E-mail:liuvjian@163.com

Wenchong Xie was born in 1978.He received his B.S.and M.S.degrees from Air Force Radar Academy,Wuhan,China,and Ph.D.degree from National University of Defense Technology,Changsha,China,in 2000,2003,and 2006,respectively.He is an associate professor with the Key Research Lab,Air Force Early Warning Academy.His research interests include space time adaptive processing,radar signal processing,and adaptive signal processing. E-mail:xwch1978@aliyun.com

Rongfeng Li was born in 1971.He received his B.S.degree from National University of Defense Technology,Changsha,China,in 1993,M.S.degree from Air Force Radar Academy,Wuhan,China in 1997,and Ph.D.degree from Air Force Engineering University,Xi’an,China in 2002.He is currently a professor in Air Force Early Warning Academy, Wuhan,China.His research interests include adaptive array signal processing and radar signal processing. E-mail:lrfzmx@aliyun.com

Fei Gao was born in 1979.He received his B.S.and M.S.degrees from Air Force Radar Academy, Wuhan,China,in 2002 and 2005,and Ph.D.degree from National University of Defense Technology,Changsha,China,in 2009.Now he is a lecturer in the Key Research Lab,Air Force Early Warning Academy,Wuhan,China.He has authored or coauthored more than 20 papers.His current research interests include airborne radar signal processing and space-time adaptive signal processing.

E-mail:gaofei2004630@163.com

Xiaoqin Hu was born in 1979.She received her B.S.and M.S.degrees from Air Force Radar Academy,Wuhan,China,in 2002 and 2005,and Ph.D.degree from National University of Defense Technology,Changsha,China,in 2009.Her current research interests are signal processing,meter-wave radar height-fnding,and weather radar.

E-mail:zhengxianwei@yeah.net

Yongliang Wang was born in 1965.He received his B.S.degree in electrical engineering from Air Force Radar Academy,Wuhan,China,in 1987 and M.S.and Ph.D.degrees in electrical engineering from Xidian University,Xi’an,China,in 1990 and 1994,respectively.From June 1994 to December 1996,he was a post-doctoral fellow with the Department of Electronic Engineering,Tsinghua University,Beijing,China.Since January 1997,he has been a full professor and the director of the Key Research Lab,Air Force Early Warning Academy.He has authored or coauthored three books and more than 100 papers.He was the recipient of the China Postdoctoral Award in 2001 and the Outstanding Young Teachers Award of the Ministry of Education in 2001.His recent research interests include radar systems,space-time adaptive processing,and array signal processing.

E-mail:ylwangkjld@163.com

10.1109/JSEE.2015.00006

Manuscript received November 08,2013.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(61102169;60925005).