Nonparametric TOA estimators for low-resolution IR-UWB digital receiver

Yanlong Zhang and Weidong Chen

School of Electrical Science and Engineering,University of Science and Technology of China,Hefei 230027,China

Nonparametric TOA estimators for low-resolution IR-UWB digital receiver

Yanlong Zhang and Weidong Chen*

School of Electrical Science and Engineering,University of Science and Technology of China,Hefei 230027,China

Nonparametric time-of-arrival(TOA)estimators for impulse radio ultra-wideband(IR-UWB)signals are proposed.Nonparametric detection is obviously useful in situations where detailed information about the statistics of the noise is unavailable or not accurate.Such TOA estimators are obtained based on conditional statistical tests with only a symmetry distribution assumption on the noise probability density function.The nonparametric estimators are attractive choices for low-resolution IR-UWB digital receivers which can be implemented by fast comparators or high sampling rate low resolution analog-to-digital converters(ADCs), in place of high sampling rate high resolution ADCs which may not be available in practice.Simulation results demonstrate that nonparametric TOA estimators provide more effective and robust performance than typical energy detection(ED)based estimators.

conditional test,nonparametric estimator,time-ofarrival(TOA),low-resolution.

1.Introduction

Thanks to extremely short duration pulses employed,impulse radio ultra-wideband(IR-UWB)radios can provide high time resolution for time-of-arrival(TOA)based ranging[1–3].Several types of ultra-wideband receivers for TOA estimation have been investigated on the basis of different a-priori information requirements and completion complexities[4–8].Although the matched flter(MF)is the optimum receiver in the additive white Gaussian noise (AWGN)channel,it may require the knowledge of received pulse shape and complex high sampling rate high resolution analog-to-digital converters(ADCs).An alternative choice to the MF receiver is the energy detection (ED)receiver for its low complexity at sub-Nyquist sampling rates[9–14].In spite of its simplicity,ED receivers suffer severely signal-to-noise ratio(SNR)degradation and require the use of suboptimal noncoherent modulation schemes like on-off keying(OOK)or pulse-position modulation(PPM)[15,16].

Another preferable choice can be made by restricting the resolution of ADCs at a low level,such as monobit(twolevel),three-level and two-bit(four-level).Low-resolution high sampling rate ADCs offer the potential to utilize the information of pulse shape and allow coherent modulation options such as binary phase shift keying(BPSK)[17]. Low-resolution quantization in IR-UWB communication applications has been researched[17–21],while further investigation is still needed to be done in IR-UWB TOA estimation.An estimator based on three-level quantization whose quantization parameters are optimized by maximizing the fsher information is analyzed in[22].Two nonuniform quantization based estimators whose quantizers are constructed by maximizing the defection and the slope of the power function are investigated in[23,24],respectively. However,their estimators require exact noise parameters and are sensitive to the change of noise distribution.

From another standpoint,TOA estimation based upon low-resolution digital receivers has a close relationship with nonparametric detection,which presents robust performance in a background noise with unknown statistical information.For instance,monobit quantization is another form of sign detector[25–27].Three-level quantization can be viewed as a dead-zone limiter detector[28] while two-bit quantization can be deemed as generalizations of the sign detector[29].These detectors exhibit a nonparametric performance with respect to the probability of false alarm by using conditional statistical tests.Therefore,nonparametric detectors for the IR-UWB digital receivers can be constructed on the base of low-resolution quantization with the help of conditional tests.The goal of this paper is to combine nonparametric detection with the characteristic of impulse shape and put forward effective as well as robust TOA estimators.

In this paper,two nonparametric TOA estimators based on the dead-zone limiter detector and generalizations of thesign detector are proposed,including three steps.The frst step quantizes the received multipath signal by the optimum quantization parameters that maximize the effciency. Then,a window flter is utilized to improve the SNR which exploits the information of pulse shape.Finally,the TOA is estimated by considering a conditional test structure for the class of symmetric probability noise density functions. Simulation results illustrate that these novel nonparametric estimators outperform traditional ED estimators.

The rest of the paper is organized as follows.The system model is provided in Section 2.Section 3 presents the proposed TOA estimation scheme.Simulation results and discussions are described in Section 4,and Section 5 summarizes the paper.

2.System model

Let the received IR-UWB multipath signal be represented as follows:

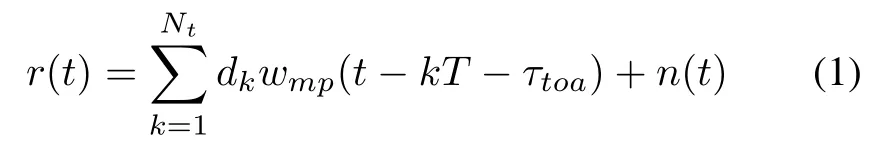
with

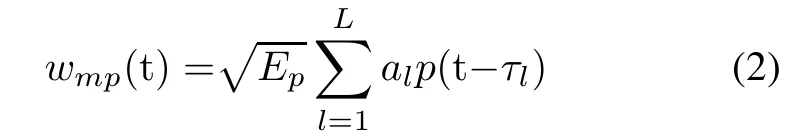
where wmpis the received pulse after the channel impulse response,p(t)is the transmitted pulse with unit energy which considers a second derivative Gaussian monocycle pulse,Epis the pulse energy,dk∈{+1,−1}is the random-polarity code of the kth transmitted symbol,Ntis the symbol number,T is the symbol duration,τland alrepresent the delays of the multipath components and fading coeffcients,respectively,and n(t)denotes the AWGN with zero-mean and variance σ2.

The received signal is fltered by a low-pass flter(LPF), and then sampled with the sampling period Ts(see Fig.1). Each symbol is sampled by N=?T/Ts?points.The ith full-resolution sample of the kth symbol rk,ican be written as

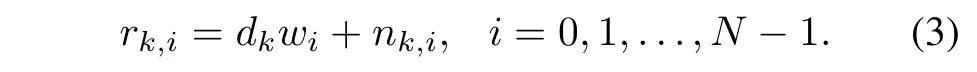
Fig.1 Low-resolution digital receiver architecture

Collect the samples as an observation vector R = [R0R1...RN−1],where Ri=[r1,ir2,i...rNt,i]T. Then rk,iis quantized according to carefully designed parameters.The test statistic is produced in the nonparametric detector based upon a conditional test structure,which presents a constant false alarm probability in additive noise with a symmetric density function assumption.Finally,the digital signal processing(DSP)section of the receiver provides the fnal TOA result.

3.Quantization and TOA estimation scheme

3.1Low-resolution quantization

TOA estimation can be treated as a binary hypothesis testing problem,where an sample vector Ri= [r1,ir2,i...rNt,i]Tis given.Then a choice has to be made between a null hypothesis H0and an alternative hypothesis H1.

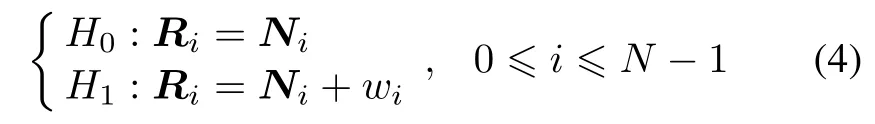
where wiis a constant,Ni= [n1,in2,i...nNt,i]Tare independent random variables representing the noise, each with identical probability density function f(x).The sign detector can be used as a nonparametric detector for this problem.This detector is based on the test statistic

The function l0(x)is a two-level approximation to the linear function l(x),defned as l(x)=x.In addition,we consider a detector based only on the signs of the samples in Riwhich satisfy|rk,i|≥c for certain c＞0[28].The resulting detector is an extension of the sign detector,and employs the dead-zone limiter lc(x)to operate the data, where lc(x)is given by

The test statistic Tc(Ri)can be written as Tc(Ri)= 2N1p−N1,where N1pis the number of Riin the interval[c,∞),N1is the number of samples which satisfy |rk,i|≥ c in Ri.The optimum value c∗for the Gaussian noise is 0.612σ[28].The nonlinearity lc(x)can be replaced by another one giving a closer approximation to the function l(x).Consider the four-level quantization of l(x)provided by the nonlinearity lc,h(x),

Then the test statistic Tc,h(Ri)can be written as Tc,h(Ri)=2N1p−N1+h(2N2p−N2),where N1pand N2pare the number of Riin the interval[c,∞)and[0,c), N1and N2are the number of samples in Riwhich satisfy |rk,i|≥ c and|rk,i|＜ c,respectively.For the Gaussiannoise,the four-level sign detector with the optimal parameters c∗=0.98σ and h∗=0.30 has the maximized effcacy[29].Equations(5),(6)and(7)can be implemented by fast comparators or low-resolution ADCs.

3.2Nonparametric detector based on conditional tests

The sign detector l0(x)is a nonparametric detector,because the distribution of its test statistic T0(Ri)under H0is distributed binomially with the probability of success p=1/2 and the number of trials n=Nt,independent of the particular probability density function f(x).In the dead-zone limiter lc(x),the samples are operated to obtain the number N1pand N1.A test function based on the test statistic Tc(Ri)cannot be the basis for a nonparametric detector for H1versus H0.This is because the distribution of Tc(Ri)under H0depends on the probability density function f(x).Although the distribution of Tc(Ri)under H0depends on the specifc f(x),it is distributed binomially under H0(conditioned on N1)with parameters p=1/2 and n=N1,independent of the f(x)with only a symmetry distribution assumption.Therefore,a nonparametric detector can be constructed based on the conditional test.

The analysis still holds for the four-level sign detector lc,h(x)(see Fig.2).Conditioned upon the value of N1and N2(N1+N2=Nt),the distribution of Tc,h(Ri)under H0is exactly known which is independent of the special f(x).This is because N1pand N2pare(conditionally) independently,binomially distributed with probability of success p=1/2 and the number of tests n=N1and n=N2,respectively.This result is an outcome of the symmetry assumption on the noise density.Besides,the three-level detector is a special case of the four-level sign detector with h=0.

Fig.2 Four-level nonparametric detector based on conditional test

In the traditional detection scheme,suppose the signal is positive,then the detector is given as

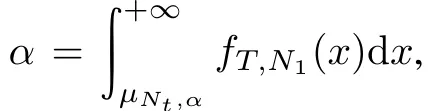
Consequently,for each outcome N1there is a conditional test based on(9)as shown in Fig.2.The only hypothesis we should make on the noise probability density function is that it is symmetric with zero-mean.The overall detection algorithm exhibits a nonparametric performance with respect to the probability of false alarm.The entries in the table of values of the threshold μNt,α(N1)do not depend on the parameter c,and the detector retains nonparametric for any value of c≥0.The table look-up is effortless to implement and its entries can easily be produced from the binomial distribution function on the basis of the system parameters Ntand α.

3.3Window flter

Let the received pulse p(t)be sampled at a rate of 1/Ts. This yields Np=Tp/Tssamples of p(t).Assuming Tpis integer multiples of Ts.If the received pulse shape is known at the receiver,a matched flter can be used to obtain decision variables for TOA estimation.However,the full resolution ideal received waveform is impractical to obtain.The matched flter can have problems of distortion, and timing mismatch.Instead,we can make use of the sign information of samples,which is insensitive to mismatch. Besides,the threshold is relatively easy to calculate when only the polar information is adopted for the nonparametric detection.As depicted in Fig.3,we adopt the second derivative Gaussian monocycle pulse with τ=0.7 ns as the transmitted pulse.

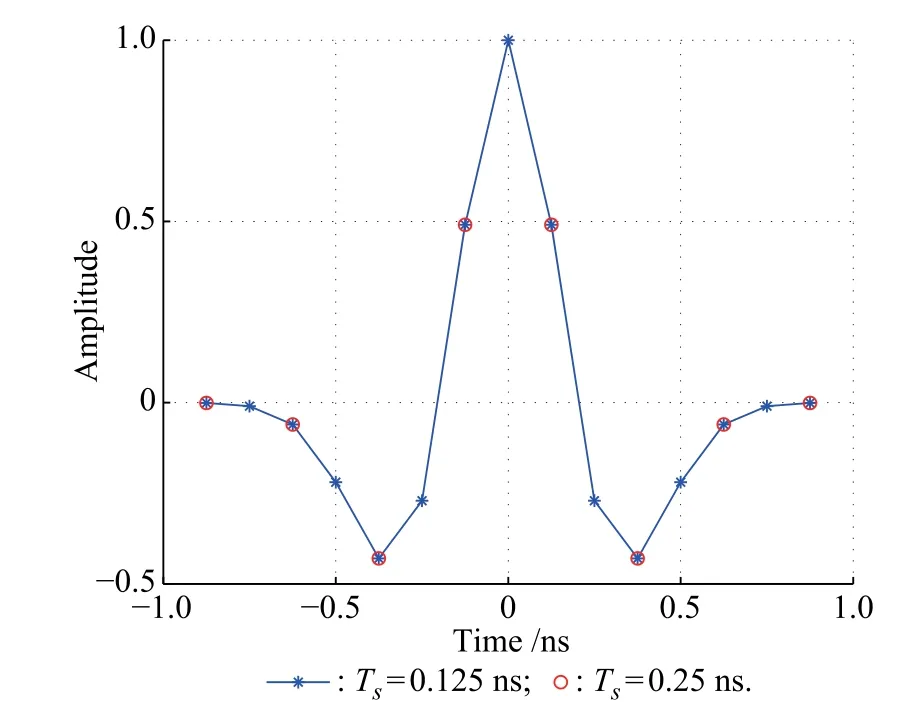
Fig.3 The second derivative Gaussian monocycle pulse with τ= 0.7 ns

In Fig.3,the sampling period is Ts=0.25ns,so we can choose the weight window as window=[−1 1 1−1]. Thus,the new test statistic can be written as

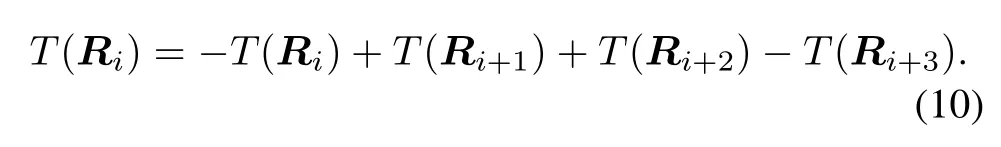
3.4TOA estimation scheme

The goal of TOA estimation is to precisely identify the frst path in received signals.A simple technique to detect the frst path is to compare the samples with the predetermined threshold.For low-resolution IR-UWB digital receivers, the received signal is sampled,quantized and then correlated with the weight window flter.The test statistic and threshold for each sampling time are obtained based on the samples.The frst sample which exceeds the threshold is likely to be the sample of the frst path.According to the previous analysis,the complete TOA scheme can be summarized as follows:

(i)Quantize the received signals by(6)or(7).

(ii)Gather the quantized samples,conduct the window flter,and obtain the test statistic Tc(Ri)or Tc,h(Ri)and the threshold μNt,α(N1).

(iii)Compare the test statistic with the threshold by(9). Then the frst sample which exceeds the threshold is the fnal TOA.

4.Simulation results and discussions

In this section,we present the simulation results of the proposed nonparametric TOA estimators.Simulations are conducted on each of the 10 000 channel realizations of IEEE 802.15.4a channel model 1(CM1),and each realization has a TOA which is uniformly distributed within (0,T).The pulse repetition interval T is set at 100 ns,and the sampling rate of the low-resolution digital receiver is fs=4 GHz.The shaping pulse p(t)is a second derivative Gaussian monocycle pulse with τ=0.7 ns,which is the parameter that determines the width of the pulse.SNR is defned as SNRΔ=Ep/N0,where Epis the symbol energy.

As shown in Fig.4,the performance of nonparametric detectors on mean absolute error(MAE)is compared with two other representative ED methods[9,10].The frst method[9]estimates TOA by utilizing a normalized threshold and the second method[10]estimates TOA by choosing the optimal threshold that minimizes MAE.ED based methods use the same sequence length Nt=50 as our methods while the integrate time is restricted to 1 ns due to the implementation limit.ξn= 0.25 and ws=30 ns are the normalized threshold and the searched back window,respectively.We fnd that the nonparametric estimators provide obvious performance improvement over ED based estimators.The three-level estimator is preferred for its simplicity and satisfactory performance while high-level estimators increase complexity with little beneft achieved.

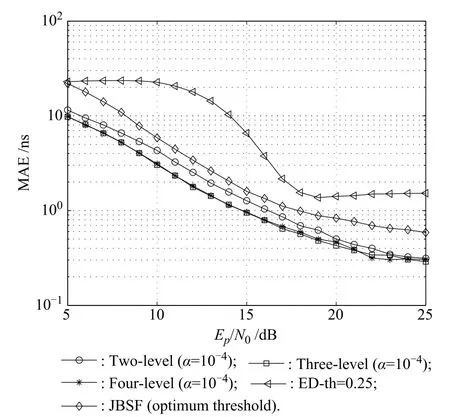
Fig.4 MAE for different estimators with respect to Ep/NO

The performance of nonparametric detectors is insensitive to deviation of the Gaussian noise variance σ2which is utilized in setting the parameter of c,as illustrated in Fig.5.

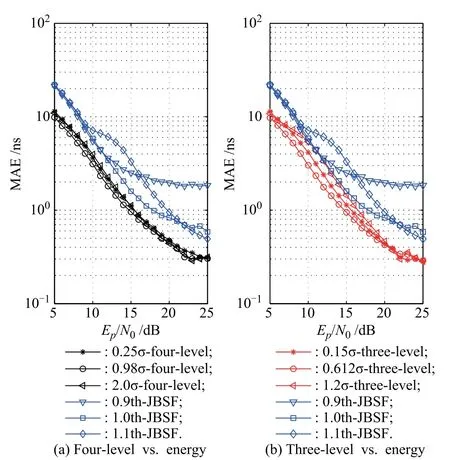
Fig.5 Performance comparison with respect to Ep/NObetween setting different values of c for nonparametric detector and setting different threshold values for energy detector

In this Fig.5,MAEs of different TOA schemes are plotted against different quantization parameter c,which im-plies c/=c∗,where c∗is the optimum value.It is observed that the estimators are close to the optimal result for a large range values of σ and the conditional test keeps its excellent performance for different c/=c∗.However,the JBSF algorithm is sensitive to the deviation of the threshold which is dependent upon the noise variance.Besides, the performance of the four-level estimator is more robust than three-level estimator.

Fig.6 shows that the proposed window flter algorithms incur 1–2 dB SNR beneft in standard UWB fading channels at the price of higher computational complexity.The improvement is obvious with SNR being10–20dB,which is therefore useful when Ntis limited.

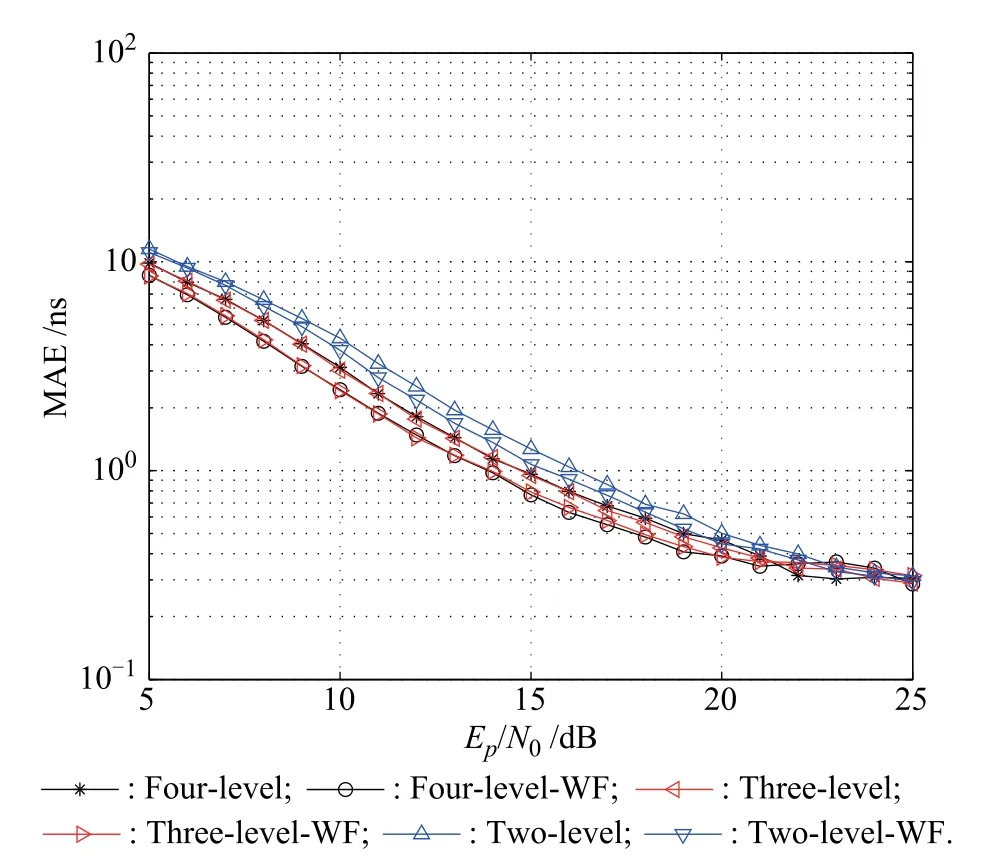
Fig.6 Performance comparison between using window flter and without using window flter for nonparametric detector

5.Conclusions

In this paper,nonparametric TOA estimators based on conditional tests have been suggested for IR-UWB applications.The TOA estimators quantize the received signal by parameters that are carefully designed.The window flter is used to improve the SNR and the conditional test provides the fnal TOA results.Simulation results indicate that our estimators give more precise and robust results compared with traditional ED based estimators.

[1]S.Gezici,Z.Tian,G.B.Giannakis,et al.Localization via ultra-wideband radios:a look at positioning aspects for future sensor networks.IEEE Signal Processing Magazine,2005, 22(4):70–84.

[2]M.Dashti,M.Ghoraishi,J.Takada,et al.High-precision timeof-arrival estimation for UWB localizers in indoor multipath channels.Novel Applications of the UWB Technologies,Rijeka:InTech,2011:397–422.

[3]D.Jourdan,D.Dardari,M.Z.Win.Position error bound for UWB localization in dense cluttered environments.IEEE Trans.on Aerospace and Electronic Systems,2008,44(2): 613–628.

[4]L.Reggiani,G.M.Maggio.Rapid search algorithms for code acquisition in UWB impulse radio communications.IEEE Journal on Selected Areas in Communications,2005,23(5): 898–908.

[5]I.Guvenc,Z.Sahinoglu,P.V.Orlik.TOA estimation for IRUWB systems with different transceiver types.IEEE Trans.on Microwave Theory and Techniques,2006,54(4):1876–1886.

[6]N.R.Jeon,H.B.Lee,C.G.Park,et al.Superresolution TOA estimation with computational load reduction.IEEE Trans.on Vehicular Technology,2010,59(8):4139–4144.

[7]B.Nadler.Nonparametric detection of signals by information theoretic criteria:performance analysis and an improved estimator.IEEE Trans.on Signal Processing,2010,58(5):2746–2756.

[8]G.Bellusci,G.J.Janssen,J.Yan,et al.Performance evaluation of a low-complexity receiver concept for toa-based ultrawideband ranging.IEEE Trans.on Vehicular Technology,2012, 61(9):3825–3837.

[9]I.Guvenc,Z.Sahinoglu.Threshold-based TOA estimation for impulse radio UWB systems.Proc.of the IEEE International Conference on Ultra-Wideband,2005:420–425.

[10]I.Guvenc,H.Arslan.Comparison of two searchback schemes for non-coherent toa estimation in ir-uwb systems.Proc.of the IEEE Sarnoff Symposium,2006:1–4.

[11]A.A.D’Amico,U.Mengali,L.Taponecco.TOA estimation with the IEEE 802.15.4a standard.IEEE Trans.on Wireless Communications,2010,9(7):2238–2247.

[12]A.Giorgetti,M.Chiani.Time-of-arrival estimation based on information theoretic criteria.IEEE Trans.on Signal Processing,2013,61(8):1869–1879.

[13]H.Ding,W.Liu,X.Huang,et al.First path detection using rank test in IR-UWB ranging with energy detection receiver under harsh environments.IEEE Communications Letters,2013,17(4):761–764.

[14]W.Liu,H.Ding,X.Huang,et al.TOA estimation in IR-UWB ranging with energy detection receiver using received signal characteristics.IEEE Communications Letters,2012,16(5): 738–741.

[15]H.Arslan,Z.N.Chen,M.G.Di Benedetto.Ultra wideband wireless communication.New York:John Wiley&Sons, 2006.

[16]Z.Sahinoglu,S.Gezici,I.Guvenc.Ultra-wideband positioning systems.New York:Cambridge University Press,2008.

[17]L.Ke,H.Yin,W.Gong,et al.Finite-resolution digital receiver design for impulse radio ultra-wideband communication.IEEE Trans.on Wireless Communications,2008,7(12): 5108–5117.

[18]J.Tang,Z.Xu,B.M.Sadler.Performance analysis of b-bit digital receivers for TR-UWB systems with inter-pulse interference.IEEE Trans.on Wireless Communications,2007,6(2): 494–505.

[19]H.Yin,Z.Wang,L.Ke,et al.Monobit digital receivers:design,performance,and application to impulse radio.IEEE Trans.on Communications,2010,58(6):1695–1704.

[20]F.Sun,H.Yin,W.Wang.Ranging implementation using fniteresolution digital receiver for IEEE 802.15.4a systems.Proc. of the IEEE Vehicular Technology Conference,2011:1–5.

[21]Y.Ma,F.Sun,W.Wang.A two-step IR-UWB acquisition method based on monobit receiver.Proc.of the IEEE International Conference on Ultra-Wideband,2011:195–199.

[22]K.Liu,H.Yin,W.Chen.Low complexity tri-level samplingreceiver design for uwb time-of-arrival estimation.Proc.of the IEEE International Conference on Communications,2011: 1–5.

[23]F.Sun,H.Yin,W.Wang.Finite-resolution digital receiver for UWB TAO estimation.IEEE Communications Letters,2012, 16(1):76–79.

[24]M.A.Lexa.Quantization via empirical divergence maximization.IEEE Trans.on Signal Processing,2012,60(12):6408–6420.

[25]J.Carlyle,J.Thomas.On nonparametric signal detectors. IEEE Trans.on Information Theory,1964,10(2):146–152.

[26]J.Fang,Y.Liu,H.Li,et al.One-bit quantizer design for multisensor GLRT fusion.IEEE Signal Processing Letters,2013, 20(3):257–260.

[27]H.Chen,P.K.Varshney.Nonparametric one-bit quantizers for distributed estimation.IEEE Trans.on Signal Processing, 2010,58(7):3777–3787.

[28]S.A.Kassam,J.B.Thomas.Dead-zone limiter:an application of conditional tests in nonparametric detection.The Journal of the Acoustical Society of America,1976,60(4):857–862.

[29]S.A.Kassam,J.B.Thomas.Generalizations of the sign detector based on conditional tests.IEEE Trans.on Communications,1976,24(5):481–487.

Biographies

Yanlong Zhang was born in 1988.He received his B.S.degree in electronic engineering and information science from Xi’an Jiaotong University, Xi’an,China,in 2005.He is currently pursuing his Ph.D.degree with the Department of Electrical and Information Science at University of Science and Technology of China,Hefei,China.His research focuses on ultrawide bandwidth time-of-arrival estimation and localization.

E-mail:zhyl007@mail.ustc.edu.cn

Weidong Chen received his B.S.degree from the Department of Electronic Engineering,University of Electronic Science and Technology of China in 1990,and M.S.and Ph.D.degrees from University of Science and Technology of China in 1994 and 2005 respectively.He is currently a professor and executive director of the Department of Electronic Engineering and Information Science,University of Science and Technology of China.His current research interests include microwave and millimeter wave technology and systems.

E-mail:wdchen@ustc.edu.cn

10.1109/JSEE.2015.00004

Manuscript received November 02,2013.

*Corresponding author.

This work was supported by the National High Technology Research and Development Program of China(863 Program)(2009AA011204).