Adaptive beamforming and phase bias compensation for GNSS receiver

Hongwei Zhao,Baowang Lian,and Juan Feng

1.School of Electronics and Information,Northwestern Polytechnical University,Xi’an 710129,China;

2.Shaanxi Fiber Home Communication Group Co.,Ltd,Baoji 721006,China

Adaptive beamforming and phase bias compensation for GNSS receiver

Hongwei Zhao1,2,*,Baowang Lian1,and Juan Feng1

1.School of Electronics and Information,Northwestern Polytechnical University,Xi’an 710129,China;

2.Shaanxi Fiber Home Communication Group Co.,Ltd,Baoji 721006,China

Adaptive antenna arrays have been used to mitigate the interference on global navigation satellite system(GNSS)receivers.The performance of interference mitigation depends on the beamforming algorithms adopted by the antenna array.However, the adaptive beamforming will change the array pattern in realtime,which has the potential to introduce phase center biases into the antenna array.For precise applications,these phase biases must be mitigated or compensated because they will bring errors in code phase and carrier phase measurements.A novel adaptive beamforming algorithm is proposed frstly,then the phase bias induced by the proposed algorithm is estimated,and fnally a compensation strategy is addressed.Simulations demonstrate that the proposed beamforming algorithm suppresses effectively the strong interference and improves signifcantly the capturing performance of GNSS signals.Simultaneously,the bias compensation method avoids the loss of the carrier phase lock and reduces the phase measurement errors for GNSS receivers.

global navigation satellite system(GNSS),space-time adaptive processing(STAP),adaptive beamforming,bias compensation.

1.Introduction

With the increasing demand of more robust global navigation satellite system(GNSS)receivers,adaptive antenna arrays have become a popular tool which allows GNSS receivers to operate in the presence of interference[1,2].Antenna arrays give the system spatial degrees of freedom to separate the desired GNSS signal from undesired interference.

In order to further improve the degrees of freedom of the antenna array,an fnite impulse response(FIR)flter is added behind each antenna element,the result set of flters is commonly referred to as space-time adaptive processing (STAP)[3].In STAP systems,the received signal from each antenna element is down-converted to the intermediate frequency(IF),then these IF signals are multiplied by the weight coeffcient,which varies the amplitude and the phase of the IF signal.Finally the weighted signals from the individual element are combined to achieve a better performance than a single antenna element[4].

The weight coeffcients of flters are controlled by the beamforming algorithm of STAP systems.Different classes of the algorithms have been utilized for this purpose.The classic adaptive algorithms include least mean square(LMS),recursive least square(RLS),direct matrix inversion(DMI),etc.For these algorithms,the required prior information of incident signals is deterministic,while the prior information is hardly obtained in GNSS applications[5].Subsequently,some blind adaptive algorithms were proposed,such as power inversion[6,7]and subspace orthogonal projection[8–10],which do not require any prior information about incident signals.

In[11],the subspace orthogonal algorithm was proposed to suppress strong interference by projecting the received signal on the interference-free subspace.After orthogonal projection,antenna arrays will bring the nulling in the direction of interference so as to mitigate the interference.Nevertheless,the desired GNSS signal is still merged into noise,which has a very low signal-to-noise ratio(SNR).These factors degrade the capturing and tracking performance of GNSS receivers.

In[12,13],the authors addressed an interference cancellation approach based on subspace tracking and the maximum SNR of the output of antenna arrays.Furthermore, in[14],the authors showed that,in the GNSS case,a better signal quality can be obtained by using optimized postcorrelated carrier-to-noise ratio(CNR)compared with the signal to interference plus noise ratio(SINR).In[15],a comparison of the maximum output SNR and the receiver CNR for adaptive antennas was performed,which demon-strates that the output SNR is an inadequate indication of the GNSS receiver CNR performance.

However,for the input signals,the adaptive array is equivalent to a spatial flter,which changes the characteristics of amplitude and phase and introduces the bias errors in code phase and carrier phase measurements of GNSS receivers[16–18].For precision navigation applications, these bias errors must be cancelled or compensated.In [19],the authors evaluated the bias errors in GNSS receivers.So far,some researchers have focused on the compensation strategy of the biases.One solution is to design specifc adaptive algorithms to prevent antenna-included bias errors[18].Another solution is to add extra fltering to compensate for the adaptive antenna effects[20].However, it is impractical to modify antenna hardware and to change adaptive algorithms for some implementations.The minimal modifcation to the existing system is attractive and practical[21,22].In[23,24],the authors addressed a code compensation strategy and a phase compensation strategy, respectively,based on the tracking loop of GNSS software receivers.However,the approach,which failed to consider compensation on the carrier loop,distorts the delay lock loop(DLL)when a bias estimation was added between the phase discriminator and the DLL flter.

To address this problem,we frstly propose a novel twostep adaptive beamforming algorithm.By this algorithm, the nulling in the direction of interference is produced to mitigate strong interference,furthermore,the interferencefree signals,multiplied by the flter weight,are obtained by the maximizing CNR of post-correlation signals to improve the signal quality.Then,we evaluate the bias errors induced by antenna arrays,and fnally we propose an improve approach for bias compensation.

The remainder of this paper is organized as follows.Section 2 discusses the signal models of STAP.Section 3 proposes a two-step adaptive beamforming algorithm combining subspace orthogonal projection and the maximum CNR of post-correlation signals.In Section 4,the effects of the adaptive algorithm on code phase and carrier phase measurements are analyzed,and then the bias compensation in the tracking loop based GNSS software receiver is proposed.Section 5 provides the experimental results of the proposed algorithm working in environments with strong interference,and simulates the bias compensation approach.Finally,we conclude the paper in Section 6.

2.Signal model

The STAP array is a multi-element antenna,each element of which is followed by a proper chain of radio frequency (RF)module and adaptive fnite impulse response(FIR). The space-time antenna model with M elements is shown in Fig.1.

Fig.1 STAP model

In Fig.1,Am(f,θ,ϕ),Fm(f)and Wm(f)denote the transfer function of antenna arrays,RF module and STAP flters,respectively.The weight in the STAP flter is denoted by wmpwhich corresponds to the pth weight of the mth flter where m ranges from 1 to M.Therefore,the weights can be combined into an MP×1 weight vector:

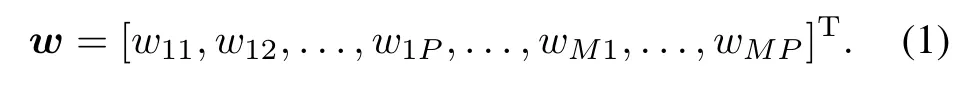
Let xm(n)denote the digitized output of the mth element,at time n,the instantaneous signal snapshot on the taps of the mth flter can be written as

Accordingly,the snapshot on each element can be denoted by an MP×1 signal vector:

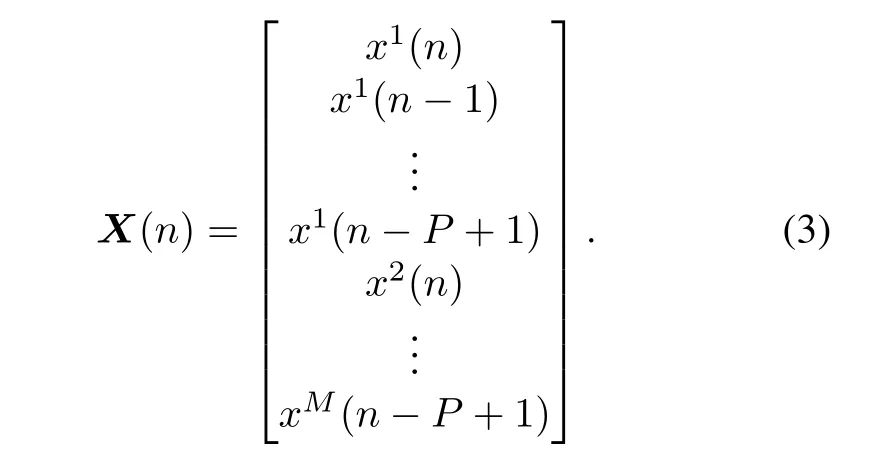
Consequently,the output of STAP can be expressed as

where H denotes the Hermitian transpose.

The weight vector is determined as the solution to an optimization problem.

In the GNSS receiver,the received GNSS satellite signal is commonly expressed as

where Psis the transmitted signal power,d(t)∈{−1,1} is the binary phaseshift keying(BPSK)data modulation, PN(t)denotes the pseudo random noise(PRN)sequence, and fcis the carrier frequency.

Consider a linear antenna array with antennas equidistant along the y-axis as shown in Fig.2,the spacing d between the two neighbouring antenna elements is half of the wavelength λ(λ=c/f0,c denotes the speed of light).The number of antenna elements is M.

Fig.2 Linear antenna array with equi-space

Assuming the azimuth angle and the elevation angle of the ith incident signal are φiand θi,respectively.The antenna geometry model and the direction of the incident signal are shown in Fig.3.

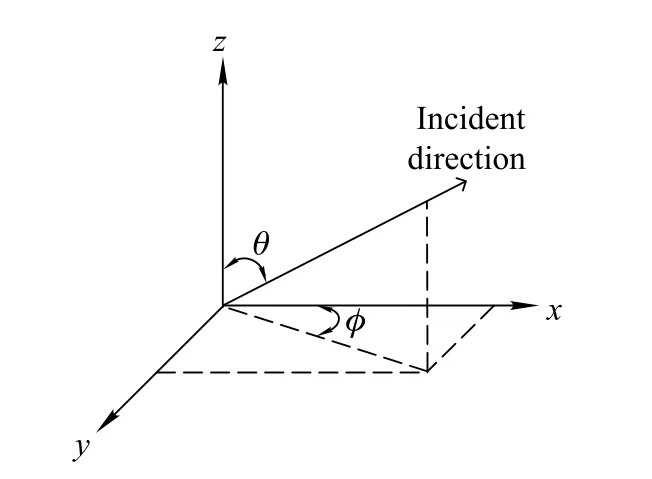
Fig.3 Antenna geometry model and direction of incident signal

The coordinate vector of the mth antenna in space is denoted by

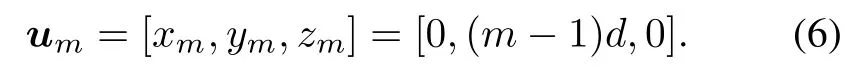
Then,the signal steering vector on array elements can be expressed as

The incident signals X(n)with GNSS signals and interference,after down-conversion and analog-to-digital (A/D)conversion,can be written as

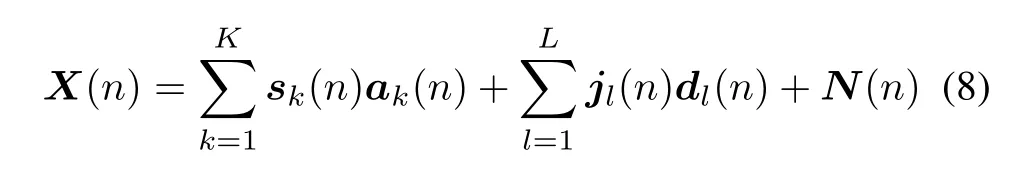
where X(n)=[x1(n),x2(n),...,xM(n)]denotes the signal vector received by M elements,sk(n)and ak(n) are amplitude and direction vectors respectively of the kth GNSS signal,jl(n)and dl(n)are amplitude and direction vectors respectively of the lth interference signal,K and L are the total number of received GNSS signals and interference signals respectively,and N(n)is Gaussian white noise with zero mean and δ2IMvariance.

The received signal which is multiplied with weights is sent to the baseband module.In the baseband module,the receiver implements the signal acquisition and tracking. The signal acquisition approach in this design is sliding correlation.The tracking loops adopt the traditional phase lock loop(PLL)and DLL[25].

3.Adaptive beamforming algorithm

Assuming that the desired GNSS signalis entirely uncorrelated with interference and background noise,the received signal can be decomposed into two orthogonal subspaces, called as signal subspace and interference subspace,respectively.The strong interference will be cancelled by projecting the received signal onto the signal subspace [26].

According to(8),the cross-covariance matrix Rxxof received signals can be denoted by

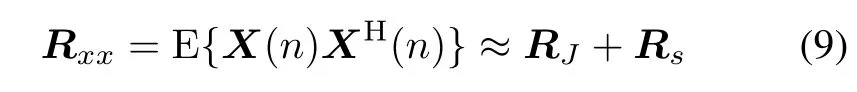
where E{·}denotes the expectation,Rsand RJare the contributions of GNSS plus noise signals and strong interference in the overall cross-covariance,respectively.

The cross-covariance Rxxhas an eigen decomposition given as

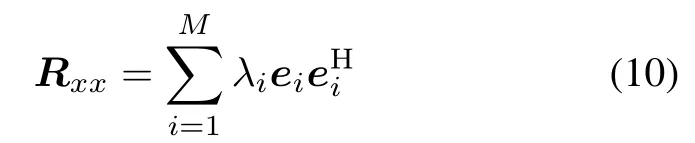
where λidenotes the eigenvalue arranged in descending, that is,λ1≥λ2≥···≥λK＞0,eiis the eigenvector corresponding to eigenvalue λi.Because the power of interference is much stronger than that of background noise and GNSS signals,the interference is dominating in the overall cross-covariance matrix Rxx.Therefore,(10)can be rewritten as

where the frst addend with L bigger eigenvalues corresponds to L strong interference signals,and smaller eigenvalues correspond to background noise and desired GNSS signals.

The eigenvectors are orthogonal to each other,and any subset of eigenvectors spans a subspace which is orthogonal to the subspace spanned by the remaining eigenvectors.Therefore,the eigenvectors e1,e2,...,eLcan bespanned to compose M by L interference subspaces,and eL+1,...,eMform M by(M−L)signal subspaces.

Denote the projection matrix of signal subspace by Pd, then

The interference-free output is

Substitute(8)into(13),then

Because of the orthogonality between the strong interference and the GNSS signal,(14)can be rewritten as

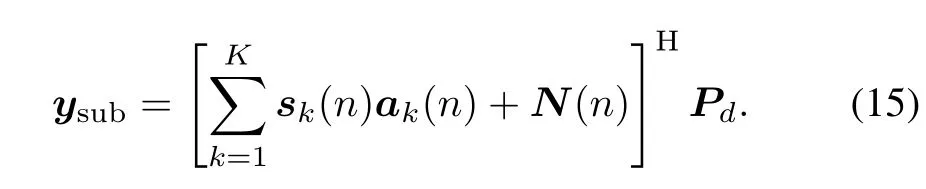
After orthogonal projection,the interference-free signal ysubis still merged into background noise.In order to enhance the interference-free signal,the maximum CNR beamforming algorithm is used to obtain weights of the STAP flter.Combining(4)with(16),the output of STAP becomes

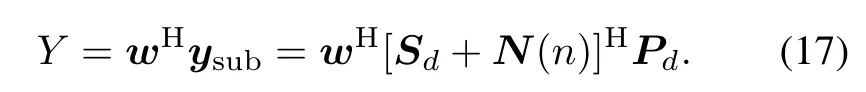
In GNSS receivers,the synchronization acquisition is a process correlating received signals with local reference codes.Taking GPS as an example,the integral period T0Nris assumed to be 1 ms for the C/A code.The crosscorrelation function can be expressed as

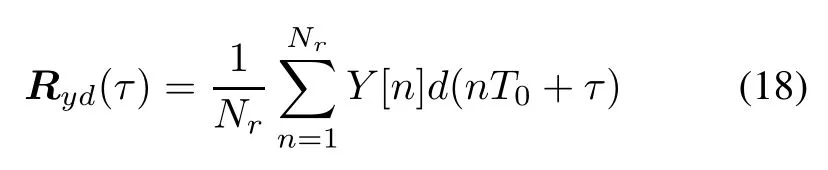
where d(t)is the locally generated reference C/A code. Substituting(17)into(18)yields

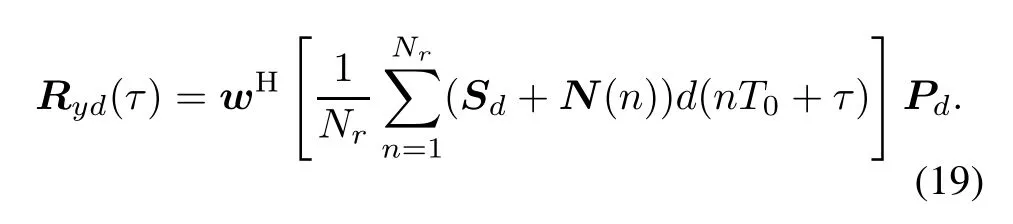
Let

Equation(19)can be rewritten as

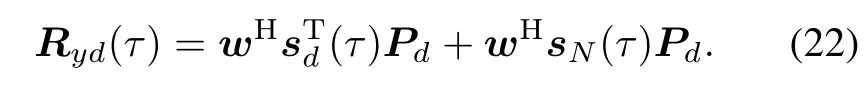
In order to derive the weights of the STAP flter that maximizes the CNR,we use an equivalent equation defned in[18].

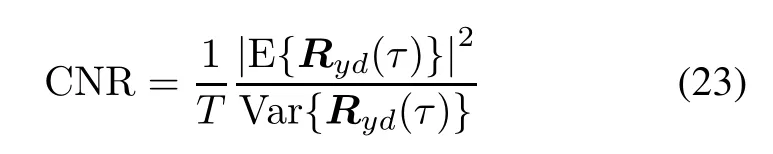
Because the reference code d(t)is a PRN with zero mean,and N(n)is Gaussian white noise with zero mean and σ2variance,the mean of Ryd(τ)is

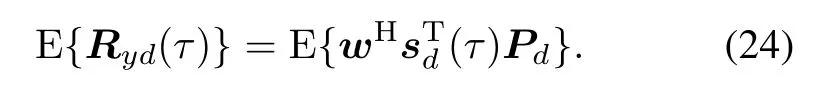
The variance of Ryd(τ)is the noise power at a particular τ.Consequently,(23)can be expressed by

The correlation matrix of the desired signal component is defned as

Then,the defnition of the CNR can be rewritten as

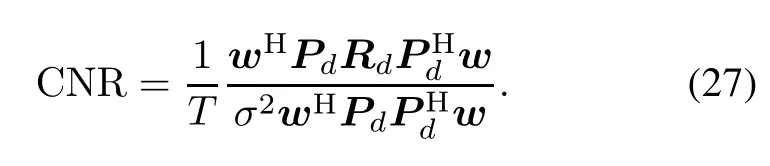
The optimum weight vector can be found to solve the general eigenvalue problem,it satisfes the eigenvalue equation:

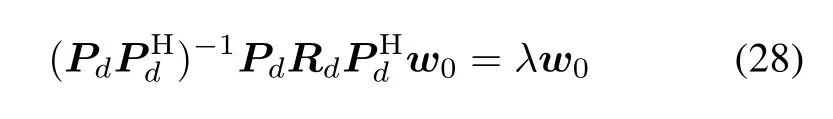
where w0is the eigenvector of(PdPHd)−1PdRdPHdcorresponding to the maximum eigenvalue.

Note that the algorithm is based on subspace orthogonal projection and the maximum CNR,the weights should be in the steady-state during the correlation.The algorithm implementation diagram in the GNSS receiver can be depicted as Fig.4.

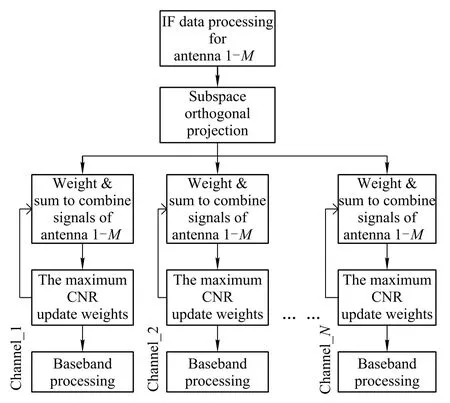
Fig.4 Adaptive beamforming algorithm fow

4.Bias estimation and compensation

Many works have established the adaptive beamforming algorithm which can distort the desired signals and cause biases in the code phase as well as carrier phase measurements.The bias errors vary widely depending on incident interference,so that deterministic bias calibration methods are not available.Furthermore,the jitter of adaptive weights will result in the tracking loop unlock.For precision GNSS applications,these biases must be compensated or mitigated.This section evaluates the biases induced by the proposed adaptive algorithm,and then proposes an improved compensation approach to correct the biases.

The received signal after carrier wipe-off in the GNSS receiver can be written as

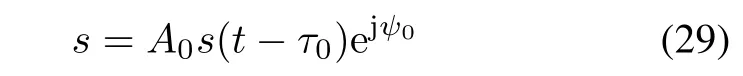
where τ0and ψ0denote the code phase delay and the carrier phase,respectively,which are the main parameters in the GNSS pseudo-range measurement.

The responses of the adaptive antenna,RF modules and STAP flters can be combined into a signal direction-dependent antenna response and be denoted by H(f,θs,φs),and then the output of arrays in the frequency domain can be expressed as

where S(f)is the Fourier transform of the received signal.

Then,the received signal correlates with the local reference pseudo random code frstly,and then the code phase delay τ0is found by searching the position of the maximum correlation value.The correlation function at time τ[27]can be expressed as

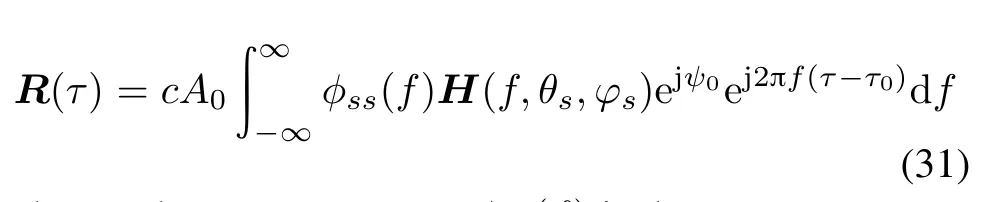
where c denotes a constant,φss(f)is the power spectrum of signal s(t).

Consequently,the estimated code phase delay τrcan be obtained as

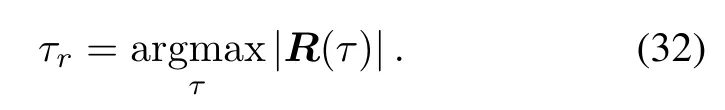
The carrier phase measurement estimation ψris the angular frequency of τr,that is,

From(31)we can see that R(τ)has a maximum at τ=τ0if H(f,θs,ϕs)=1,at which point the code phase delay and carrier phase estimations are unbiased.However,for adaptive antenna arrays,H(f,θs,ϕs)varies according to the incident direction of the received signal.The correlation function R(τ)is related to the variables θsand φs. Thus the estimation value is introduced into biases by the adaptive antenna.

In order to mitigate these biases,more practically it is desirable to have a bias compensation strategy which applies generally and requires minimal modifcation to existing GNSS receivers.This section proposes a simple approach to the estimate the code phase bias,as well as the carrier phase bias.

In the DLL of GNSS receivers,the code phase delay can be evaluated by the cross-correlation at the two fxed delays[23],

where Tcis the PRN chipping rate,T0is the fxed phase delay.

For the carrier phase bias estimation,we need only to evaluate the prompt value of the cross-correlation,that is,

Equations(34)and(35)provide a perfect estimation and a correction for the phase biases.Therefore,we can mitigate the biases by compensating Δτ and Δψ in the GNSS receiver.Fig.5 shows the compensation diagram,where NCO represents the numerically controlled oscillator,and PVT represents position-velocity-time.

Fig.5 Bias compensation scheme based on receiver tracking loop

5.Simulations

5.1Signal scenario

Consider a linear antenna array with seven elements and assume that there is a GNSS signal and two strong interference signals on antenna arrays.The two interference signals are continuous-wave interference and wideband interference,and their incident directions are–50°and 60°, respectively.The incident direction of the GNSS signal is 30°.

In the GNSS software receiver,the received signal is transformed to IF after down-conversion and A/D conversion.Let the carrier frequency in the GNSS signal model be 4.092 MHz and the pseudo random code ratio be 1.023 MHz.Let the sampling frequency and the sampling period be 16.384 MHz and 1 ms,respectively.Moreover, we assume that the SNR is–25 dB and the interferenceto-signal ratio is 60 dB.And the continuous-wave interference has the same frequency with the GNSS.The received signal in the time and frequency domain is shown as Fig. 6.

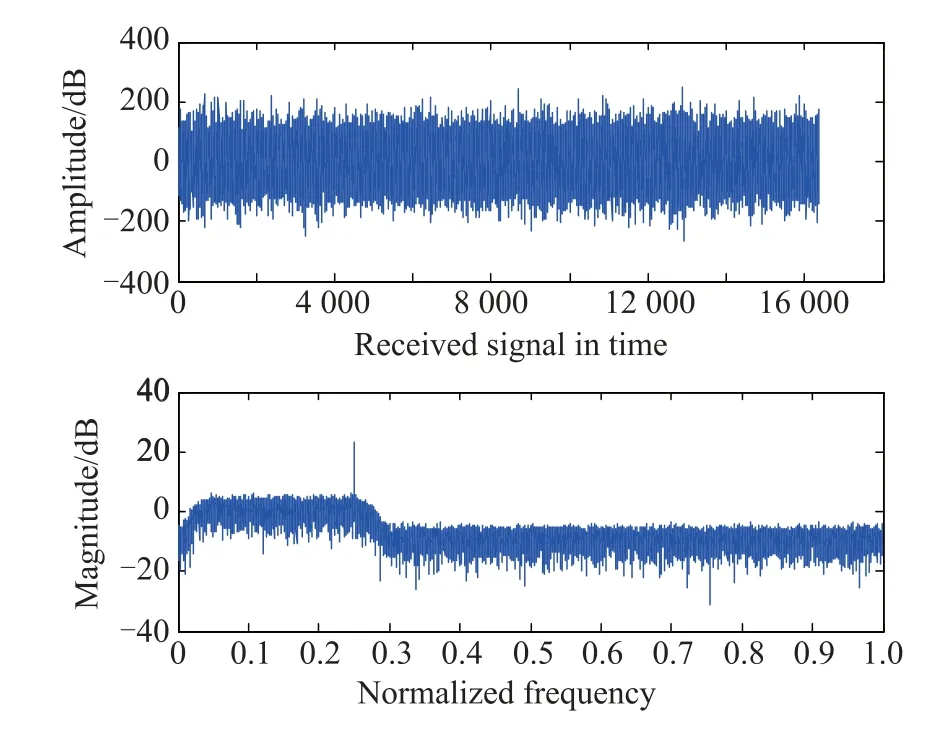
Fig.6 Received signals on antenna array

5.2Interference suppression performance

After subspace orthogonal projection,the adaptive antenna array produces nulling in the direction of interference, thus the interference will be suppressed.Fig.7 shows the interference-free signal in the time and frequency domain. From the spectrum graph we can see the strong interference have been mitigated.

Fig.7 Interference-free signal after subspace projection

However,the desired GNSS signal is still merged into background noise.In order to enhance the desired signals, we apply the maximum CNR constraint for interferencefree signals.The beam pattern comparison is obtained by using the subspace projection algorithm and the joint flter algorithm respectively as shown in Fig.8.

Fig.8 Pattern by using subspace projection algorithm and joint algorithm

Furthermore,the interference-free signal enters into the baseband processing module for correlation operation.It is assumed that the code delay is 200 chips and the correlation period is 1 ms.Then,the correlation value after sliding one period is shown as Fig.9.

Fig.9 Correlation without the maximum CNR

From Fig.9,we can see that the correlated peak occurs in the suitable position so as to capture the desired GNSS signal.However,due to the affects of background noise, the correlated value has a great jitter.Therefore,the performance of signal capturing and tracking will be degraded.

Then,the proposed beamforming algorithm is applied for interference-free signals.After weighting,the correlated calculation of the received signal is conducted with the reference C/A code.The correlated diagram is shown as Fig.10.

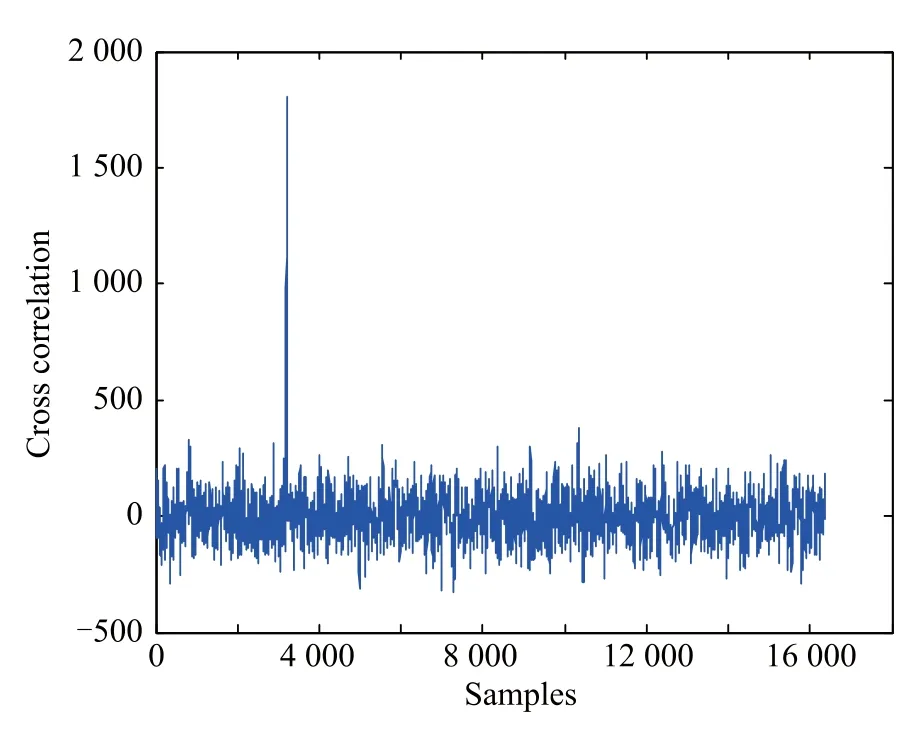
Fig.10 Correlation with subspace projection and the maximun CNR

From Fig.10,we can clearly see that the peak of the cross-correlation value is larger than that without the maximum CNR so that the signal can be tracked steadily and the reliability of the receiver also can be improved.

5.3Bias compensation performance

The section demonstrates the compensation of adaptive antenna-induced biases using the proposed algorithm in the previous section.The interference signal scenario is identical to those described in the above section,and the incident elevation angle of the GNSS signal is varied.We compare the two adaptive algorithms which are the proposed joint beamforming algorithm and the power inversion(PI)algorithms respectively.

Fig.11 shows the compensation result using the proposed beamforming algorithm.The original code delay biases and the residual biases after compensation are compared.From Fig.11 we can fnd that the code delay bias before compensation reaches 80 cm,and by the proposed compensation method,the bias is only about 1 cm.We also note that the original code delay has a drop-off when the GNSS signal is very close to the interference.The reason is that the desired signal which is very close to the interference will not be able to support signal acquisition. Therefore,it is clear that the code delay bias compensation method exhibits near-perfect bias correction.

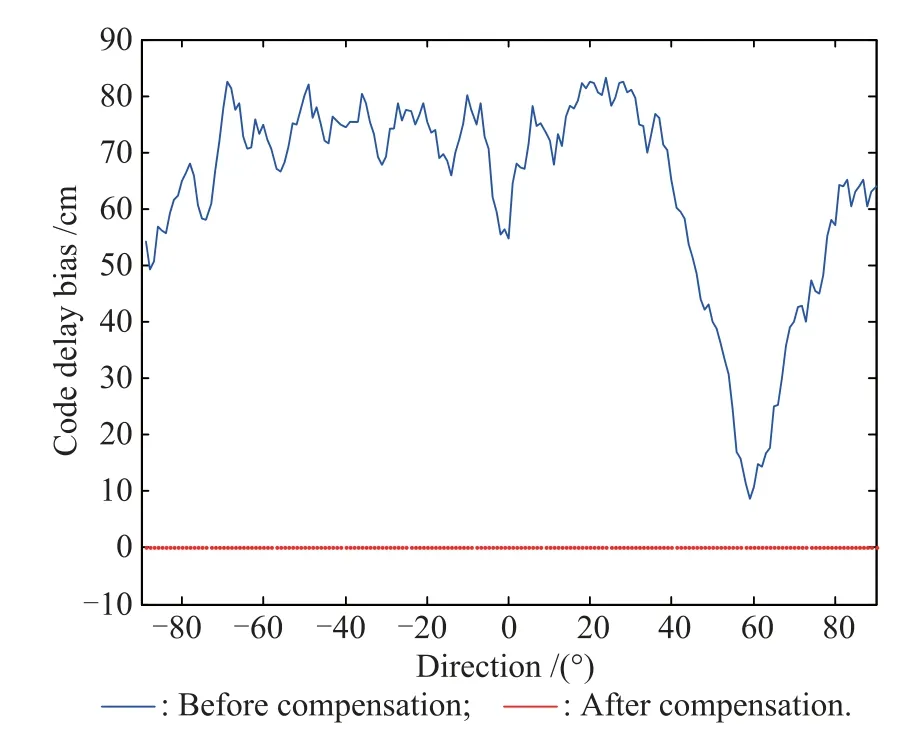
Fig.11 Code phase bias using the joint beamforming algorithm

Fig.12 shows the compensation performance in the same scenario but using the power inversion algorithm. The code delay bias before compensation has reached 250 cm,which is larger than that using the joint beamforming algorithm.However,from Fig.12 we can see that,by the proposed compensation method,the bias is dropped to less than 1 cm perfectly.

Fig.12 Code phase bias using the power inversion algorithm

6.Conclusions

The adaptive antenna array as an attractive tool for interference suppression has been widely used in GNSS receivers. In this paper,we frstly propose a novel adaptive algorithm to perform interference mitigation and to increase the CNR of post-correlation signals.The strong interference can be effectively mitigated by using subspace orthogonal projection,and then,the maximum CNR constraint is used to enhance the desired signal.Moreover,we analyze the biases induced by the adaptive antenna and propose a bias compensation approach.Finally,we validate the proposed algorithm by simulations.The simulation results show that the proposed beamforming algorithm can suppress the strong interference and improve the signal capturing and tracking performance.Additionally,the proposed bias compensation approach can perfectly mitigate the biases.

[1]A.Javier,F.Carles,C.Pau.Antenna array based GNSS signal acquisition for interference mitigation.IEEE Trans.on Aerospace and Electronic Systems,2013,49(1):223–243.

[2]D.Saeed,J.Ali,B.Ali,et al.A low-complexity GPS antispoofng method using a multi-antenna array.Proc.of the Institnte of Navigation GNSS Conference,2012:1233–1243.

[3]R.L.Fante,J.J.Vaccaro.Wideband cancellation of interference in a GPS receive array.IEEE Trans.on Aerospace and Electronic Systems,2000,36(2):549–564.

[4]J.Gupta,T.D.Mppre.Space-frequency adaptive processing for radio frequency interference mitigation in spread-spectrum receivers.IEEE Trans.on Antennas and Propagation,2004, 52(6):1611–1616.

[5]A.Soloviev,Van F.Graas.Beam steering in global positioning system receivers using synthetic phased arrays.IEEE Trans.on Aerospace and Electronic Systems,2010,46(3):1513–1522.

[6]S.J.Kim,R.A.Iltis.STAP for GPS receiver synchronization.IEEE Trans.on Aerospace and Electronic Systems,2004, 40(1):132–144.

[7]Y.T.H.Morton,L.L.Liou,D.M.Lin,et al.Interference cancellation using power minimization and self-coherence properties of GPS signals.Proc.of the 17th International Technical Meeting of the Satellite Division,2004:132–143.

[8]U.Madhow.Blind adaptive interference suppression for direct-sequence CDMA.Proceedings of the IEEE,1998, 86(10):2049–2069.

[9]W.Gong,X.Sun.An improved reduced-rank STAP interference suppression method indesign of GNSS receivers.Science China Information Sciences,2012,55(10):2329–2342.

[10]X.Zhang,H.Yuan,Y.Gong,et al.The navigation satellite selection using a subspace adaptive genetic algorithm for high earth orbits in multi-GNSS scenarios.Proc.of the International Technical Meeting of the Institute of Navigation,2013: 172–179.

[11]W.Utschick.Tracking of signal subspace projectors.IEEE Trans.on Signal Processing,2004,50(4):769–778.

[12]R.Wang,M.Yao,Z.Cheng,et al.Interference cancellation in GPS receiver using noise subspace tracking algorithm.Signal Processing,2011,91(2):338–343.

[13]Y.Hou,W.Guo,X.Jin.Design of an anti-jamming GPS receiver based on orthogonal projection method.Journal of Systems Engineering and Electronics,2010,21(1):16–19.

[14]J.W.Betz.Effect of partial-band interference on receiver estimation of C/N0:theory.Bedford:MITRE Corporation,2001.

[15]A.J.O’Brien,I.J.Gupta.Comparison of output SINR and receiver C/N0for GNSS adaptive antennas.IEEE Trans.on Aerospace and Electronic Systems,2009,45(4):1630–1640.

[16]D.S.De Lorenzo,J.Rife,P.Enge,et al.Navigation accuracy and interference rejection for an adaptive GPS antenna array. Proc.of the 19th International Technical Meeting,2006:763–773.

[17]F.Xiang,G.S.Liao,C.Zeng.Compensation method for code tracking error of GPS induced by space-time adaptive processing.Systems Engineering and Electronics,2013,35(1):15–19.(in Chinese)

[18]A.J.O’Brien,I.J.Gupta.An optimal adaptive fltering algorithm with zero antenna-included bias for GNSS antenna arrays.Navigation,2010,57(2):87–100.

[19]I.J.Gupta,C.Church,A.J.O’Brien.Prediction ofantenna and antenna electronics induced biases in GNSS receivers.Proc.of the 19th International Technical Meeting,2007:650–656.

[20]U.S.Kim.Mitigation of signal biases introduced by controlled reception pattern antennas in a high integrity carrier phase differential GPS system.Stanford:Stanford University,2007.

[21]P.B Anantharamu.Space-time equalization techniques for new GNSS signals.Alberta:University of Calgary,2011.

[22]G.A.McGraw,C.McDowell,J.M.Kelly.GPS anti-jam antenna system measurement error characterization and compensation.Proc.of the 19th Institute of Navigation GNSS International Technical Meeting of the Satellite Division,2006:705–714.

[23]A.J.O’Brien,I.J.Gupta.Mitigation of adaptive antenna induced bias errors in GNSS receives.IEEE Trans.on Aerospace and Electronic Systems,2011,47(1):524–538.

[24]S.K.Kalyanaraman,M.S.Braasch.GPS adaptive array phase compensation using a software radio architecture.Navigation, 2010,57(1):53–68.

[25]B.W.Parkinsin,J.J.Spilker.Global positioning system:theory and applications.Washington D.C.:AIAA,1996.

[26]H.W.Zhao,B.W.Lian,J.Feng.Adaptive beamforming algorithm for space-time interference suppression in GNSS receivers.Systems Engineering and Electronics,2012,34(7): 1312–1317.(in Chinese)

[27]C.Church.Estimation of adaptive antenna induced phase biases in global navigation satellite systems receiver measurements.Ohio:The Ohio State University,2009.

Biographies

Hongwei Zhao was born in 1980.He received his B.S.degree in communication engineering from Zhengzhou University,Zhengzhou,China, in 2001.Then he received his M.S.and Ph.D. degrees in communication engineering from Northwestern Polytechnical University,Xi’an, China,in 2006 and 2012,respectively.And he is currently a lecturer and post-doctor in Northwestern Polytechnical University.His research interests include satellite navigation and positioning,adaptive array processing,and embedded systems.

E-mail:hongvi zhao@126.com

Baowang Lian was born in 1962.He received his B.S.,M.S.and Ph.D.degrees in communication engineering from Northwestern Polytechnical University,Xi’an,China,in 1983,1986 and 2007,respectively.Since 1999,he has been a professor with the School of Electronic Information in Northwestern Polytechnical University.He has more than 50 research articles,and more than 2 inventions.His research interests include navigation positioning systems,wireless communications,and embedded systems.

E-mail:bwlian@nwpu.edu.cn

Juan Feng was born in 1982.She received her B.S.degree in communication engineering from Northwestern Polytechnical University,Xi’an, China,in 2005 and M.S.degree in information system engineering from Northwestern Polytechnical University,in 2009.She is currently pursuing the Ph.D.degree in communication and information system at Northwestern Polytechnical University.Her research interests are wireless communications,adaptive signal processing and wireless sensor network. E-mail:fengjuankh@hotmail.com

10.1109/JSEE.2015.00002

Manuscript received March 17,2014.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(61301094)and the Postdoctoral Science Foundation of China (2014M552490).