针对一般式多变量逻辑函数的化简方法与技巧

张 辉 李 竹

（1．山西师范大学临汾学院自然科学系，山西 临汾 041000；2．山西师范大学物信学院，山西 临汾 041004）

针对一般式多变量逻辑函数的化简方法与技巧

张 辉1李 竹2

（1．山西师范大学临汾学院自然科学系，山西 临汾 041000；2．山西师范大学物信学院，山西 临汾 041004）

卡诺图化简逻辑函数是最常用的一种方法。本文针对一般式多变量逻辑函数的化简，提出了一种不用转化为标准式，而直接在卡诺图中表示的方法，从而大大提高了化简的速度和效率。

卡诺图；多变量；直接表示

1 函数表达式的化简及方法比较

众所周知，在数字电路设计中，逻辑函数表达式的复杂程度决定着实际电路的稳定性、成本高低和市场竞争力。根据较复杂的逻辑函数表达式制造出来的实际电路成本较高，稳定性较差，市场竞争力不强。所以，逻辑函数的化简始终是数字电路设计中一项重要的工作。目前业界常用的逻辑函数化简法有代数法化简和卡诺图法化简。代数法化简必须对公式的记忆及运用技巧达到一定的熟练程度，而且化简之后，结果是否最简，还需要有一定的判断力才能做出决定。相比之下，卡诺图化简法不失为一种简洁方便的化简方法，所以得到了广泛的应用。

2 关于卡诺图化简法

卡诺图化简法是1953年卡诺（Karnaugh）在维奇（W. Veitch)的图形法化简逻辑函数的思想上提出来的。其基本原理是代数法化简中的吸收律1，即针对两逻辑相邻项，可消去取值不同的变量，保留取值相同的变量。卡诺图化简法的具体步骤是：

(1)将所给的逻辑函数的一般式转化为最小项标准式（若所给即为最小项标准式，该步骤省略）；

(2)将所得的最小项标准式用卡诺图表示；

(3)根据最小项合并规律，用圈在卡诺图中圈住所有为“1”的方格，并在圈旁写出每个卡诺圈的化简结果；

(4)将每个卡诺圈的化简结果“或”起来，即得化简结果。在实际操作中，卡诺图化简法有以下注意事项：

(1)卡诺图化简只适用于最小项标准式，所以，若所给函数不是最小项标准式，应先利用代数法或真值表法将该函数转化为最小项标准式。

(2)所圈卡诺圈要尽可能地大。因为根据相邻最小项合并规律可知，卡诺圈越大，该卡诺圈消去的变量就越多，结果中保留的变量就越少，越简单。

(3)不能出现多余圈。保证每个卡诺圈中至少有一个“1”未被其它圈圈住，否则，该圈就是多余圈。

(4)卡诺圈尽可能地少。每个卡诺圈都对应一个与项，所以，少一个卡诺圈在结果中就少一个与项，实际电路就少一个与门。

3 针对一般式在卡诺图化简法中的改进

在上述卡诺图法化简步骤中，我们可以看到，针对一般式，首先得把一般式转化为最小项标准式才能应用卡诺图来化简。按照本文提出的方法，可以将一般式的各项直接填入卡诺图中，不必进行最小项标准式的转化。这样可以大大提高设计电路时的工作效率，并且降低错误率。

一般式中，缺变量的与项在卡诺图中填充“1”的方法：

(1)一个缺变量的与项在卡诺图中填充“1”的数目为2n（n为该与项中所缺变量的个数）。

(2)缺变量的与项在卡诺图中填充的“1”方格应为逻辑相邻关系。

(3)在缺变量的与项中，先不考虑所缺的变量，以现有的变量取值为依据，找出应该填充的具体位置。

一般式中最小项填充“1”的方法跟标准式中最小项填充“1”的方法相同，此处不再赘述。

4 实用举例

解 可以看出，该式为四变量的一般式。

第一步：按照上述方法将各与项在卡诺图中相应位置填充上“1”。D应填充两项，位置分别在m3、m11上；B应填充四项，位置分别在m4、m5、m12、m13上；应填充两项，位置分别在m1、m5上；A应填充两项，位置分别在m10、m11上。如图1所示。

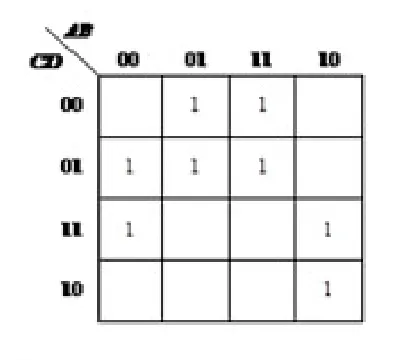
图1 填充结果

第二步：根据画圈原则，在图中圈住所有为“1”的方格，如图2所示。

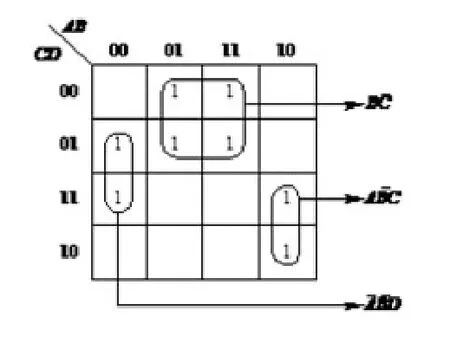
图2 圈住所有为“1”的方格

第三步：根据上一步结果，写出化简后的新函数。

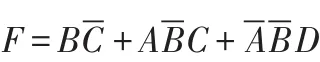
5 结束语

综上所述，针对逻辑函数一般式的卡诺图化简，经理论和实践证明，采用本文提出的方法，可以省去一般式转化为最小项标准式的步骤，提高了化简速度和正确率。

[1]周良权，方向乔．数字电子技术基础（第二版）[M]．北京：高等教育出版社，2002．

[2]江小安，董秀峰，张军，等．数字电子技术（第三版）[M]．西安：西安电子科技大学出版社，2008．

[3]蒋志勇，陈锡华，熊川．卡诺图在多变量逻辑函数化简中的应用[J]．桂林航天工业高等专科学校学报，2006，44(4)：4-5．

[4]许斌．浅析逻辑函数的卡诺图化简法[J]．河北能源职业技术学院学报，2004，(4)：82-84．．

[5]窦新旺，张庆胜．逻辑函数的卡诺图化简法[J]．开封教育学院学报，2002，(4)：65-66．

[6]杜海林．数字电路中逻辑函数的卡诺图化简法[J]．淮海工学院学报，2011，(21)：413-414．

Methods and Skills for Simplification of the General Formula and Multivariable Logic Function

Zhang Hui1Li Zhu2

(1.Linfen College,Shanxi Normal University,Linfen 041000,Shanxi; 2.Physics and Information Engineering College,Shanxi Normal University,Linfen 041004,Shanxi)

Karnaugh map is one of the most commonly used method of logic function.In view of simplification of the general formula and multivariable logic function,this paper proposes a method that doesn't need to translate into standard type,but to represent in Karnaugh map directly,thus greatly improving the speed and efficiency of simplification.

Karnaugh map;multivariable;direct representation

TP302

A

1008-6609(2015)10-0088-02

张辉，男，山西临猗县人，硕士研究生，助教，研究方向：人工神经网络与智能信息处理。