高RDX含量改性双基推进剂非等温反应动力学和热危险性

贾昊楠，安振涛，江劲勇，贾海东，谢永亮

(1．军械工程学院，石家庄 050000;2．军械技术研究所，石家庄 050000;3．92207部队，石家庄 050100)

List of symbols

ms(b)Mass of sample or closed－bomb

TstepTemperature step of ARC test

twaitScanning waiting time

s Sensitivity

EaApparent activation energy，kJ·mol－1

Eo(k)Value of Eaby Ozawa’s or Kissinger’s method，kJ·mol－1

Ao(k)Pre－exponential factor by Ozawa’s or Kissinger’s method，s－1

β Linear heating rate，℃·min－1

T0Onset temperature，℃

TpPeak temperature，℃

R Gas constant，J·K－1·mol－1

α Fraction of conversion

f(α)Kinetics mechanism differential function

G(α)Kinetics mechanism integral function

TeOnset temperature of non－isothermal decomposition，℃

Te0Tecorresponding to β→0，℃

ΔHdExothermic heat，J·g－1

r Linear correlation coefficients

TbCritical temperature of thermal explosion，℃

Q Standard mean square deviation

Q0Total heat of reaction，J

Φ Thermal inertia factor

ΔTadTemperature rise under adiabatic condition，℃

TfFinal temperature of decomposition，℃

MmaxMaximum exothermic rate，℃·min－1tadAdiabatic time－to－explosion，min PmaxMaximum pressure，bar

PmaxM－1Maximum pressure per unit mass，bar·g－1

PmaxrMaximum pressure rate，bar·min－1

MT，sTemperature rise rate of system，℃·min－1

MTPhi－corrected MT，s，℃ ·min－1

TD24Environment temperature when tad=1440 min，℃

k Reaction rate constant

0 Introduction

Since CMDB propellant containing ammonium nitrate has the advantages of high energy，low signature and good combustion performance，etc．，it has become the priority selection of the propellant species on tactical missiles and high－tech rockets［1］．Besides，in order to meet the requirements of the range of fire，the contents of high energy explosive(RDX)，for example，is gradually increased［2］．

GHT－1A is a domestic developed CMDB propellant with higher RDX content up to 48．5%．For containing a mass of high explosives，CMDB propellant not only has a strong self－decomposed characteristic，but also has an overall detonable property．Scholars at home and aboard always highly focused on the thermal hazard studies about explosives，as well as primary explosives，however less on CMDB propellant，especially with a mass of high energy solid．The risk of spontaneous combustion or detonation exists in the process of manufacture，storage and transportation of CMDB propellant，probably due to the self－decomposition and heat accumulation．Therefore，the non－isothermal decomposition kinetics，the specific heat capacity，adiabatic decomposition and the thermal hazard of GHT－1A is researched in this article．

1 Experimental

1．1 Sample

The sample used in the experiment is the CMDB propellant GHT－1A composed of 20．0%(mass fraction)of NC，21．5%of NG，48．5%of RDX，and 10．0%of other auxiliary additives．

1．2 Equipment and conditions

1．2．1 TG experiment

TG－DTG curves under the atmosphere of high purity nitrogen gas(flowing rate，20 cm3·min－1;atmospheric pressure)was obtained by using TGA1(Perkin Elmer Co．，USA)．The conditions of TG were as follows:about 1．50 mg sample;heating rate:10 ℃·min－1．

1．2．2 DSC experiment

In this article，DSC apparatus used is DSC8000(Perkin Elmer Co．，USA)．A small amount of sample(about 1 mg)was added into an aluminum－sealed crucible under the atmosphere of high purity nitrogen gas(flowing rate，20 cm3·min－1;atmospheric pressure)．It was heated at constant rates(2．5，5，10，15，20 ℃·min－1)in the temperature ranging from 100℃to 300℃．

1．2．3 Specific heat experiments

The specific heat capacity of GHT－1A was tested by μRC(THT Co．，UK)in five different temperatures(25，50，75，85，95 ℃)．The sample mass is 517．57 mg．

1．2．4 ARC experiment

ARC curves under the adiabatic condition were obtained by using an ARC(THT Co．，UK)．A titanium alloy closed－bomb was used in the experiment．The sample is 203．02 mg．The test conditions are listed in Table 1．

Table 1 Test conditions of ARC experiment

2 Results and discussion

2．1 Non-isothermal thermal decomposition behaviors of GHT-1A

TG－DTG curve at 10 ℃· min－1and DSC curves at different heating rates of the sample are shown in Fig．1 and Fig．2，respectively．The results show that there are two stages of the thermal decomposition of GHT－1A，and one decalescence process of RDX with the summit peak at 202．5 ℃ in DSC curves．The first exothermic peak is attributed to the decomposition of NC and NG，corresponding to 48．7%mass loss．The melting process of RDX，though，lies in the end of Stage 1，the heat absorbed is much lesser than the heat released．Stage 2 is caused by the exothermic decomposition reaction of RDX，accompanied by 34．6%mass loss，and there are still a few residues at the end of decomposition．

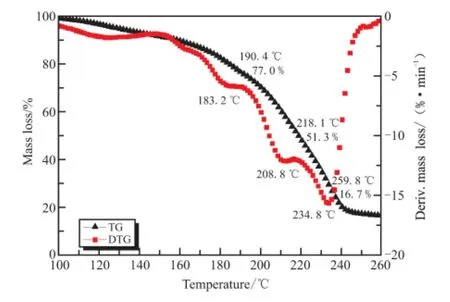
Fig．1 TG-DTG curves at heating rate of 10 ℃·min－1

2．2 Evaluation of non-isothermal reaction kinetics

In order to obtain the kinetic parameters(apparent activation energy(Ea)and pre－exponential constant(A))of the exothermic decomposition reaction for GHT－1A，two multiple heating methods，Kissinger’s method and Ozawa’s method［3－4］，were employed．The original values(Te，Tpand ΔHd)of the two exothermic decomposition reactions are listed in Table 2．The values(E，A and r)determined by Kissinger’s method and Ozawa’s method are shown in Table 3．

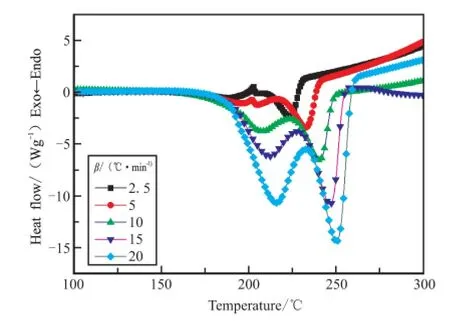
Fig．2 DSC curves at different heating rates

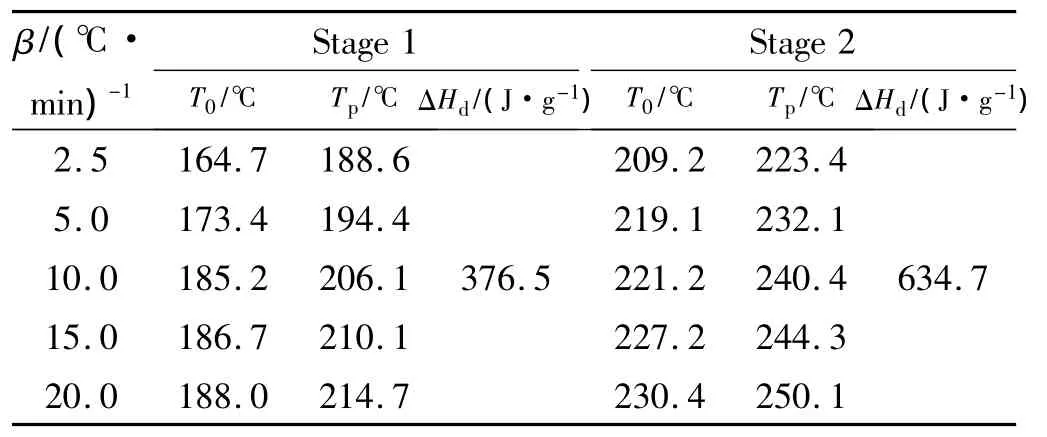
Table 2 Parameters obtained from DSC curves at different heating rates

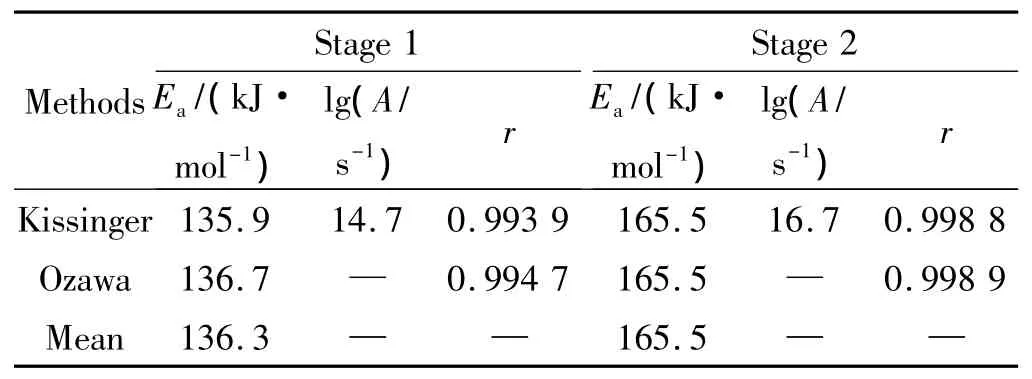
Table 3 Reaction kinetics determined by Kissinger’s method and Ozawa’s method

From the results，it can be seen that the Ekis in good accordance with Eo，besides that the linear correlation coefficients r are all very close to 1．The results are credible．

To explore the thermal decomposition mechanism of the two exothermic reaction stages，DSC curves at heating rates of 2．5，10，20 ℃·min－1were dealt with mathematic means．Four integral Equ．(1)～ (4)listed in Table 4 were employed［5－9］．

Forty－one types of kinetic model functions［5］and DSC data listed in Table 5 were put into the integral equations above，respectively and for calculations．The values of Ea，lgA，r and standard mean square deviation Q were obtained by the linear least－squares method．The most probable mechanism function is selected by the better values of r and Q．The results are listed in Table 6．

Table 4 Kinetic analysis methods

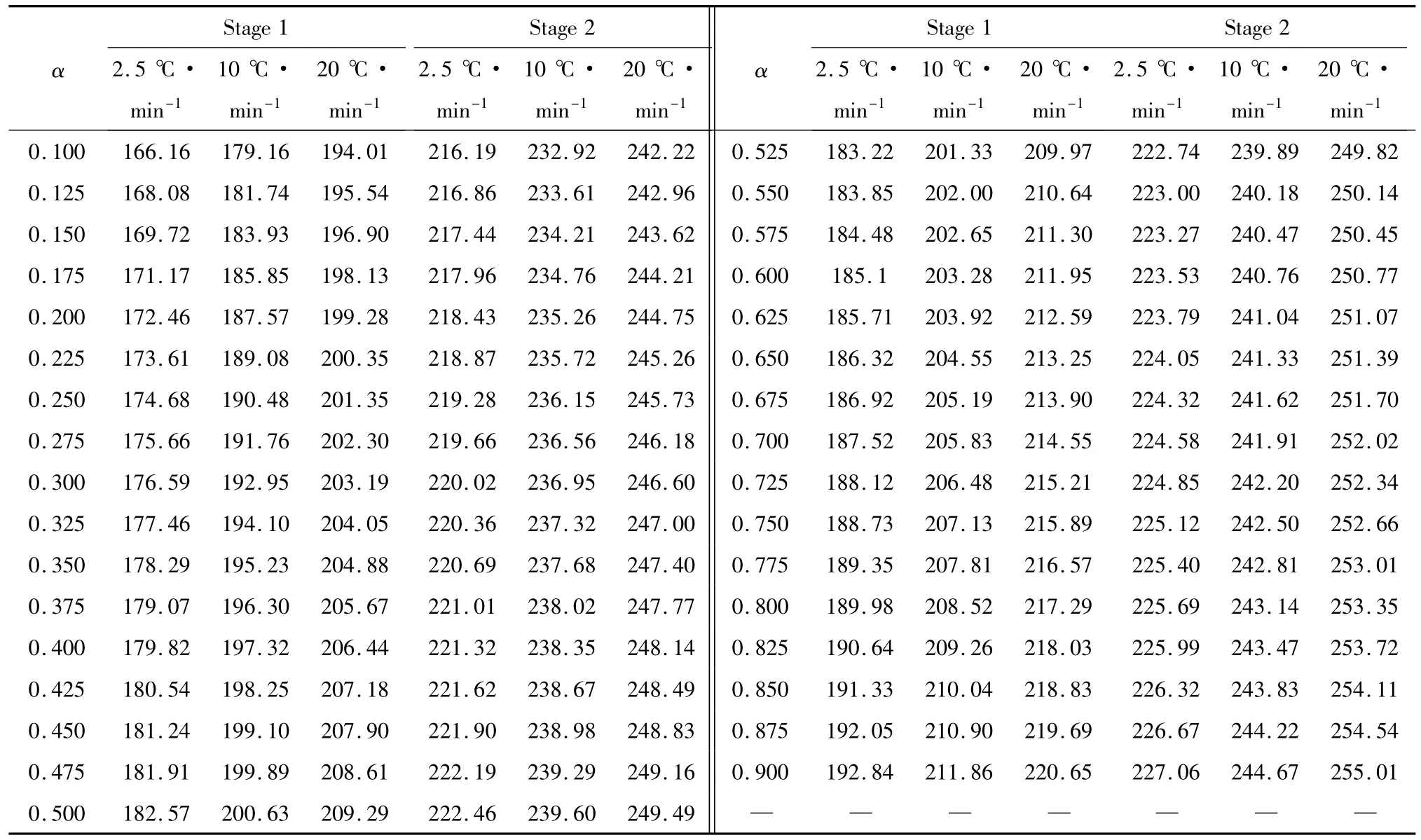
Table 5 Data for decomposition processes of sample at different heating rates from DSC curves

It can be seen that the values of Eaand lgA obtained from a single non－isothermal DSC curve are in approximately good agreement with the values calculated by Kissinger’s method and Ozawa’s method．So that，the reaction mechanism of the two exothermal decomposition processes are both classified as nucleation and growth，and the mechanism function is the Avrami－Erofeev equation．The probable kinetic model functions of the processes are as follows:

Stage 1:

Stage 2:

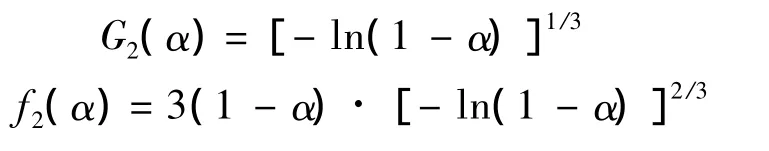
Substituting f(α)，Eaand A into Equ．(5):

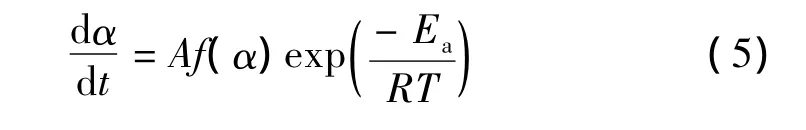
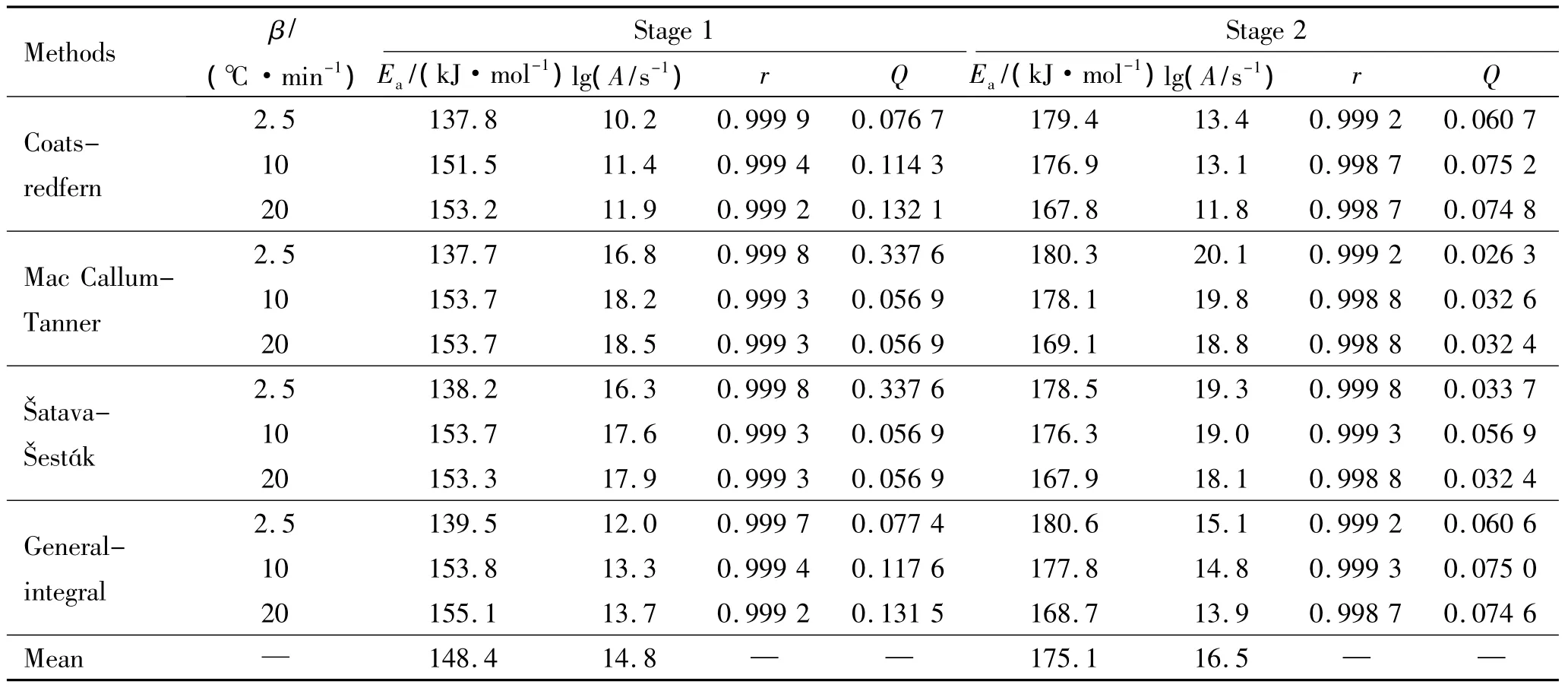
Table 6 Kinetic parameters of the exothermic decomposition realtion of GHT-1A

The kinetic equation of exothermal decomposition reaction can be described as:

Stage 1:

Stage 2:

2．3 Evaluation of critical temperature of thermal explosion(Tb)

where b，c and d are all coefficients［10］．Te0of the two stages are 150．4 ℃ and 200．1 ℃，separately．

The corresponding Tbobtained from Equ．(7)［5，11］using the above－mentioned values of Te0，Eoof stage 2 is 212．0 ℃．

The value Te0of the onset temperature Tecorresponding to β→0 obtained by using the data of βiand Teiof stage 1 and 2 in Table 2．Te0were calculated using:

2．4 Evaluation of specific heat capacity and adiabatic time-to-explosion

As a result of using large amount of sample and wide range of measuring temperature，μRC has high accuracy and high application value in estimating credible cpin wider range of temperature．

The determination and polynomial fit result of the cpof GHT－1A are shown in Fig．3．The result shows that the cpwith temperature is cp=4．96×10－7T3－4．61 ×10－4T2+0．14T－14．07 in the temperature range of 298．1 ～368．2 K．

Fig．3 Measurement results of cpof GHT-1A

The adiabatic time－to－explosion is time from the beginning of thermal decomposition to thermal explosion of sample under adiabatic conditions［12－15］．It is an important parameter to evaluate the thermostability of energetic materials intuitively．It can be calculated by following Equ．(8)．

Considering that T001=Te01，Tend1=Te02，and submitting dynamic equations，the specific heat capacity functions and corresponding experimental results in to Equation，the adiabatic time－to－explosion can be worked out directly，and it is 22．7 min．

2．5 Adiabatic decomposition behaviors of GHT-1A

ARC is an effective means for evaluating thermal hazard of reactive chemicals［16－19］．It can show the overall process of exothermic decomposition for a mass of sample and even the explosion under the adiabatic condition．

Fig．4 Curves of temperature rate，pressure rate and temperature

The relationship bamong temperature rate，pressure rate and temperature of GHT－1A．is shown in Fig．4，The decomposition process can also be divided into two parts，just like the former results．In the temperature range of 140．8 ～187．1 ℃，the double－base components of NC and NG decompose slowly．With increasing of reaction depth，temperature rate rises up slowly at first and then decreases slightly，and the heat of sample accumulates gradually．In this stage，GHT－1A releases a small amount of gaseous product．After that，the reaction becomes violent．The selfheating rate as well as pressure rate rises up sharply in a very short time．And it corresponds to reaction of RDX．

Actually，the temperature recorded by ARC is not the real temperature of sample but the system of sample and closed－bomb．In the ideal adiabatic condition，the reaction heat should be devoted entirely to heating up the sample itself．Therefore，it is necessary to modify the experimental data by thermal inertia factor φ before applying them into practice［20－21］．The expression of φ is as follows:

The thermal decomposition characteristics of GHT－1A is shown in Table 7．The temperature data is modified by φ，while the pressure data remains the same．Four important parameters derived from ARC experiment are onset temperature T0，time－to－explosion tad，adiabatic temperature rise ΔTad，and maximum pressure per unit mass Pmax·M－1．Since the self－heating speed is concerned with temperature and time，the first two are the evaluation criteria for possibility of thermal explosion［22］．The severity of explosion effect can be judged by the latter ones．It can be seen that the autocatalytic reaction of GHT－1A begins at a high temperature，and takes a long time to arrive at explosion．The great gaseous product and heat of the reaction will finally cause huge damage．

Table 7 Thermal decomposition characteristics of GHT-1A(φ=12．6)

On the other hand，T0obtained from ARC experiment is 11．5 ℃ lower than Te0from DSC experiment．While，tadis 8．9 min shorter than that estimated by cpand DSC data．

2．6 Evaluation of adiabatic reaction kinetics and TD24

In adiabatic system，Eaand A can be calculated by the following equation:

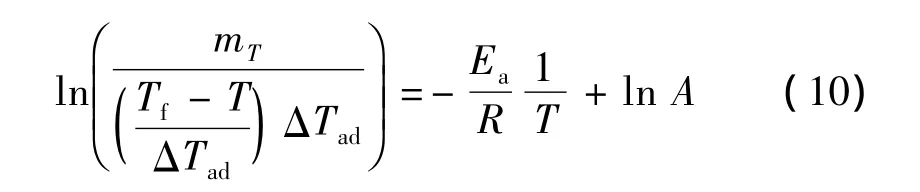
Since the reaction speed of the first process of decomposition reaction is much slower than the second one，it becomes the rate－controlling step．Therefore，the kinetic triplet of the first step is just need to be considered．Origin software is used to see the linearity of the raw data as shown in Fig．5．The reaction order n calculated is 1，Eais 196．8 kJ mol－1，lgA is 46．4 s－1，and the linear correlation coefficient is high:0．998 1．

Fig．5 Linearity of lnk and

TD24is the temperature when tadequals to 1 440 min．The following formula is used to infer the relationship between the onset temperature and tad:

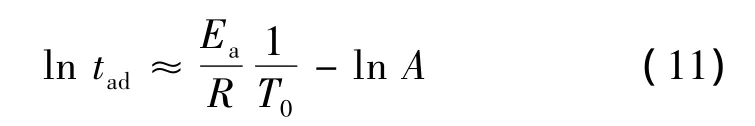
The calculated parameters and the φ－corrected tadare substituted into the Equ．(11)．TD24of GHT－1A is obtained:120．8 ℃．

3 Conclusion

(1)The non－isothermal thermal behavior of GHT－1A studied with TG－DTG and DSC can be divided into two exothermic decomposition stages．The kinetic equations can be expressed respectively as:

Stage 1:

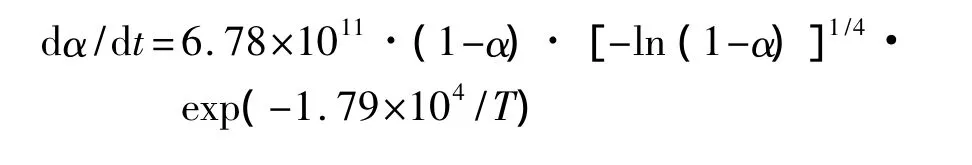
Stage 2:

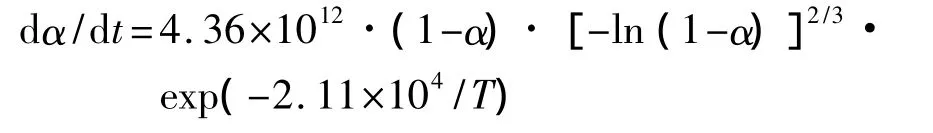
The values of Eaand lgA of the two stages are 148．4 and 175．1 kJ·mol－1，14．8 and 16．5 s－1，respectively．The critical temperature of thermal explosion is 212．0℃．The equation of specific heat capacity for GHT－1A determined with μRC is cp=4．96×10－7T3－4．61×10－4T2+0．14T－14．07(298．1 K＜T＜368．2 K)．The adiabatic time－to－explosion tadis 22．7 min based on the evaluation of cp．

(2)The adiabatic thermal behavior of GHT－1A studied with ARC can also be divided into two stages．The raw temperature data recorded by ARC are not real but significant．It can reflect the worst case by means of modifying by inertia factor．The values of T0is 138．9 ℃;tadis 13．8 min;ΔTadis 1 415．3 ℃;Mmis 3 243．8 ℃ ·min－1;PmM－1is 131．0 bar g－1．

(3)Judging from DSC and ARC results，there are notable differences in T0and tad．It can be perceived that the data from ARC reflects a worse case of thermal decomposition for GHT－1A．Therefore，based on the point of safety assessment，ARC experiment should be considered seriously．

(4)The thermal hazard of GHT－1A was analyzed from two aspects，the self－heating speed and the possibility of explosion．Since TD24is 120．8 ℃，GHT－1A has a good thermal stability，but a great attention also should be paid during manufacture，transportation，use，and storage for its great severity of explosion effect．

［1］ Zhang L Y，Zhu X H，Wang J N．Thermal decomposition of composite modified double－base propellant with high solid content［J］．Chin．J．Explo．＆ Propell．2011，34(5):74－77．

［2］ Yao N，Liu Z R，Wang J N．Effect of RDX content on dynamic mechanical properties of modified double－base propellants［J］．J．Propul．Tech．，2008，29(4):498－501．

［3］ Kissinger H E．Reaction kinetics in differential thermal analysis［J］．Anal．Chem．，1957，29(11):1702－1706．

［4］ Ozawa T．A new method of analyzing thermogravimetric data［J］．B Chem．Soc．Jpn．，1965，38(11):1881－1886．

［5］ Hu R Z，Shi Q Z．Thermal analysis kinetics［M］．Beijing:Science Press;2001．

［6］ Mac Callum J R，Tanner J．The kinetics of thermogravimetry［J］．Eur．Polym．J．，1970，6(7):1033－1039．

［7］ Šatava F，Šesták J．Computer calculation of the mechanism and associated kinetic data using a non－isothermal integral method［J］．J．Therm．Anal．，1975，8(3):477－489．

［8］ Agrawal R K．A new equation for modeling nonisothermal reactions［J］．J．Therm．Anal．，1987，32(1):149－156．

［9］ Wu XM，Liu JH，Li W，Qi CS．Thermal decomposition kinetics of complexes of rare earth with amino acid RE(Val)Cl3·6H2O(RE=Nd，Sm)［J］．Acta．Phys－Chim．Sin．，2006，22(8):942－946．

［10］ Wang C C，Wang B L，Huang J，Liu W．Influence of RDX on thermal safety of composite explosive［J］．Explo Mater．，2012，41(2):8－15．

［11］ Gao H X，Zhang H，Zhao F Q．Kinetic behaviour of the exothermic decomposition reaction of n－guanylurea dinitramide［J］．Acta．Phys－Chim．Sin．，2008，24(3):453－458．

［12］ Xu K Z，Song J R，Zhao F Q，et al．Thermal behavior，specific heat capacity and adiabatic time－to－explosion of G(FOX－7)［J］．J．Hazard．Mater．，2008;158(2－3):333－339．

［13］ Xu K Z，Song J R，Zhao F Q，et al．Special heat capacity，thermodynamic properties and adiabatic time－to－explosion of 1，1－Diamino－2，2－dinitroethylene［J］．Acta．Chim．Sin．，2007，65(24):2827－2831．

［14］ Smith L C．An approximate solution of the adiabatic explosion problem［J］．Thermochim．Acta．，1975，13(1):1－6．

［15］ Roduit B，Dermaut W，Lunghi A，et al．Advanced kineticsbased simulation of time to maximum rate under adiabatic conditions［J］．J．Therm．Anal．Calorim．，2008，93(1):163－173．

［16］ Bhattacharya A．A general kinetic model framework for the interpretation of adiabatic calorimeter rate data［J］．Chem．Eng．J．，2005，110(1－3):67－78．

［17］ Dong Y，Hiroshi K，Kazutoshi H．Predicting the self－accelerating decomposition temperature(SADT)of organic peroxides based on non－isothermal decomposition behavior［J］．J．Loss．Prev．Process．Ind．，2003，16(5):411－416．

［18］ Yu J Y，Chen L P，Peng J H．Thermal hazard research of smokeless fireworks［J］．J．Therm．Anal．Calorim．，2012，109(3):1151－1156．

［19］ Lin W H，Wu S H，Shiu G Y，et al．Self－accelerating decomposition temperature(SADT)calculation of methyl ethyl ketone peroxide using an adiabatic calorimeter and model［J］．J．Therm．Anal．Calorim．，2009，95(2):645－651．

［20］ Townsend D I，Tou J C．Thermal hazard evaluation by an accelerating rate calorimeter［J］．Thermochim．Acta．，1980，37(1):1－30．

［21］ Jia H N，Lu G E，Jiang L M，An ZT，et al．Study on adiabatic decomposition properties and dynamics mechanism of double－base propellant by accelerating rate calorimeter(ARC)［J］．Chin J Explo ＆ Propell．，2013，36(5):77－81．

［22］ Stoessel F．Thermal safety of chemical processes:risk assessment and process design［M］．Switzerland:Weiley－Vch Verlag GmbH ＆ Co．KGaA;2008．