合成纤维在水中的分散手段与表征方法

关晓宇 钱晓明 杨棹航

(天津工业大学纺织学院，天津，300387)

湿法成网是非织造成网方式的一种，它源自传统的造纸业。其原理是将纤维原料在水介质中混合分散制成纤维浆料，再将浆料输送到成网机构，在湿态下脱水成网再加固成非织造布。传统造纸行业将植物纤维作为纤网的基本原料，再配以分散剂、黏合剂等助剂制成浆粕。随着产品要求的不断升级，越来越多的产品开始尝试加入不同性能的化学纤维、金属纤维等一系列非传统植物纤维［1］制成非织造布或功能纸，不同的合成纤维具有不同的特性，所以能赋予纤网不同的特性。与天然纤维相比，合成纤维在力学性能、化学稳定性及特殊功能性等方面具有明显优势，在提高力学性能的同时赋予抗菌、抗静电、阻燃等其他多种特殊功能。

与传统湿法抄造所使用的植物纤维不同，合成纤维由于自身所固有的特性，例如纤维的刚度、长度、吸湿性及相对密度等问题，使得合成纤维在进行湿法抄造时存在诸多问题，例如由于合成纤维的吸湿性能和表面电荷不同于植物纤维，所以在悬浮液中的分散性能很差，容易产生絮聚现象，导致纤网成型均匀度较差，同时在生产中还容易产生一系列其他问题［2］。

1 合成纤维的分散方法

1.1 改变纤维性状促进分散

1.1.1 根据堆积因子调整纤维长径比

20世纪90年代，Kerekes和Schell在前人概念的基础上提出了堆积因子的概念［3］，用N表示直径相当于纤维长度的球形体积内纤维的数目：

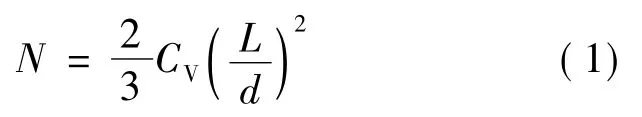
式中：CV——体积浓度;

L——纤维长度;

d——纤维直径。

在纤维-水体系研究中，对纤维长径比加以控制可以得到匀度较好的纸页［4］。当N较小时纤维在液相中的分布趋于一致;当N逐渐增大时纤维的流动性能明显下降，逐渐絮聚难以被分散［5］。根据堆积因子公式，减小纤维长度、增加纤维直径、降低浆料体积浓度能够有效地降低堆积因子N的大小，从而达到促进纤维分散的效果。以一些涤纶分散试验为例，合适的分散长径比约为500∶1，低于300∶1 不利于分散，高于700∶1 则纤网强力过低［6］。很多试验研究根据堆积因子将合成纤维短切并抄造成网，长度多在4 mm以下，以此增强合成纤维的分散效果。但也有研究人员指出，单纯地以切短纤维或混合植物纤维来应对分散问题而回避其他技术难题，这样抄造出来的纤网很难满足工业领域应用的高性能要求［7］。

1.1.2 纤维改性

利用合成纤维制造湿法非织造布的主要难题在于合成纤维的疏水性。虽然合成纤维或植物纤维在制造纤网的工序上大致相同，但两种纤维的化学性质差别很大，主要是由于合成纤维疏水性强，在水中不易分散并容易絮聚，很难形成连续均匀的纤网。针对合成纤维的疏水性能，很多研究人员尝试对纤维进行改性处理，改善其亲水性，使其能在水中分散得更均匀，满足湿法抄造的要求。改性方法多以物理或化学方法为主，通过接枝改性、腐蚀纤维表面等物理或化学方法使纤维表面结构发生变化，在一定程度上改善纤维的亲水性能［8-11］。具体的亲水改性与纺织纤维研究中的方法大抵相同，但由于方法复杂不利于大规模生产，在产业化发展方面比其他分散方法应用得少。

1.2 动力分散

在纤维悬浮液中施加动力是促使纤维分散的主要方法。合成纤维由于自身的疏水性将纤维束放入水中时直接絮聚成一团并具有一定强力，无法自然均匀地分散成纤网，同时纤维束本身也存在并丝缠绕等状态而非全部单根散纤维状态，这就需要施加剪切力来克服其他力促使纤维分散。Shiffler于1985年针对纤维动力分散提出了一个剪切力不等式［12］：

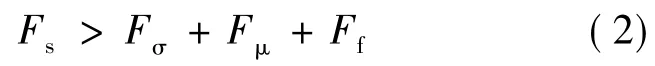
式中：Fs——施加在纤维束上的剪切力;

Fσ——表面张力;

Fμ——阻力;

Ff——垂熔力。

只有当施加在纤维束上的剪切力满足此不等式并且持续一定时间时，纤维束才会打开分散成单根纤维状态;如果剪切力不够，即使时间再长也不会分散纤维，依然会在纤网上留下疵点［13］。除此之外，调整施加动力的频率也能改善纤维的絮聚情况，并且在多种纤维混合抄造的情况下起到有效混合的作用。有研究证明，施加动力将纤维束分散成单纤维，在此基础之上加入分散剂能有效地维持这种分散情况［14］。

除了促使纤维束打开分散之外，研究动力形成湍流能够帮助预测纤维的运动和悬浮轨迹，以及纤维在纤网中的取向和排列，从而赋予非织造布更多的结构变化并扩展产品的应用范围［15-17］。

1.3 化学试剂分散

利用化学试剂促进合成纤维在悬浮液中分散是目前产业化应用最广、研究最多的一种方式，同时采用分散剂的布面疵点要明显少于不采用分散剂的布面疵点［18］。根据合成纤维表面电荷的不同，按照纤维分散机理选择相应的离子型或非离子型分散剂。在目前的试验研究和生产中，分散合成纤维多采用CMC(羧甲基纤维素)和PEO(聚氧化乙烯)等高分子分散剂［19-22］，提高悬浮液浓度，限制纤维在水相中的自由度;同时在纤维表面形成润滑膜，以减小纤维纠缠的可能性，对短纤维起到一定的助流效果。此外，在一些针对碳纤维、玻璃纤维和陶瓷纤维等其他合成纤维分散的试验中，使用与纤维表面电荷相同或相反的离子分散剂来分散纤维也能得到不错的效果。例如大部分合成纤维和无机纤维表面带负电荷，加入CPAM(阳离子聚丙烯酰胺)或SDS(十二烷基硫酸钠)等阳离子型分散剂，在一定分散条件下效果甚至高于PEO等高分子分散剂［23-25］。在这类具有很强电荷特性的合成纤维悬浮液中，使用相反电荷离子分散剂成网可能更为均匀［26］。同时分散剂的质量分数大小也是影响因素之一，太低无助于分散，太高则会影响分散系的流动性［27］，对后续抄造纤网造成阻碍。

国外对于湿法非织造纤维分散剂的研究与国内基本一致，略有不同的是在分类上根据对纤网的辅助功效分为两种类型：一种是低分子量试剂，可帮助纤维润湿和在水中分散;另一种是通过调节悬浮液黏度，防止长纤维形成纤维长串，同时提高非织造布的外观匀整度［18］。

2 合成纤维分散程度的表征

对不同试验条件下纤维的分散程度进行表征评价是研究的重要环节。不同研究领域根据自身工艺特点对纤维分散程度的表征也有不同的标准和手段，例如造纸行业反映纤维分散程度常使用打浆度来表示［28-30］。对于一般的纤维分散程度表征方法主要分为两类，一类是通过直观方法对纤网或产品进行分析，另一类则是通过测定分散剂水溶液的表面张力、动电电位和吸光度等参数来表征纤维的润湿或分散性能。

纤维、箱体系统、湍流、分散的质量及稳定性都会对纤网表面的疵点造成影响。国外针对纤维分散程度的表征主要集中在合成纤维在纤网或布面上留下的疵点方面，研究人员将纤维形成的疵点分成四种形式：并排粗节疵点、绳结状疵点、熔融疵点和纤维团状疵点［31］。

2.1 直观对比

将不同参数条件下合成纤维在溶液中沉淀后的图片进行直观对比是最直接的表征方式，因其操作方式简单故得以广泛应用，但这种方法也有许多不足。首先，这种对比仅仅是图像的对比，并不能对纤维分散程度进行一定的量化表达，只能定性说明;其次，在某些场合改变工艺参数后纤维的分散程度很接近，分散程度的差别无法通过肉眼清晰地观测出，直观对比方法在这种场合无法起到直观的表征作用。

2.2 ζ电位

如图1所示，根据斯特恩双电子层理论，存在斯特恩层和扩散层两部分，滑动面与溶液本体之间的电势差称为ζ电位［32］，是对颗粒之间相互排斥或吸引力强度的度量，同时反映分散的稳定性。ζ电位绝对值越高，静电斥力越大，分散体系越稳定，纤维越容易分解;反之，电位绝对值越低，分散体系越倾向于凝聚。由此可见，分散体系的稳定性与ζ电位有一种依存关系，所以在不同行业中经常用ζ电位来表征添加分散剂后悬浮溶液整体的稳定性或分散程度［33-34］。通过对ζ电位的研究可以有效辅助试剂的添加，但也有试验证明，ζ电位的影响因素很多，同时测量方式也存在一定的差异。

1 斯特恩双电子层模型

2.3 亮度直方图

利用光的投射原理得到浆料体系或纤网成型后的图像，对该图像进行分析，将光学信号转化为数字信号，得出图像上不同区域的亮度直方图分布或者相应的灰度等级［35］，再通过一定算式得出浆料或非织造布的均匀系数，这种通过图像亮度分布来分析并表征图像均匀度的方法在很多行业早有应用。以分析图像为主，图像获取和分析操作都较为简单，在多个学科都有应用并有相应的检测仪器。也有试验指出，虽然运用亮度直方图的分布及相应的均匀指数具有一定的说服力，但在某些情况下，例如纤网面密度对分散均匀的影响并不能准确地反映出来;同时纤维的颜色、透明度和毛羽都会对均匀指数产生一定的影响，这种指数只是在面密度和纤维颜色相近的条件下对比纤维分散性能才有效果［36］。除了图像分析上的局限之外，图像采集时摄像头进光量的大小、物体背光均匀性和连续性等问题也会影响图像的亮度分布变化。根据这一应用限制，不少研究人员在亮度直方图的基础上开发出一系列评价指标及测试手段来改进这一缺陷［37］，但设备和操作都过于复杂，反而限制了应用。

2.4 布面疵点形式

如上所述，国外的相关研究将合成纤维分散不均匀分为四种疵点形式，在一些文献中对分散程度的表征也以疵点作为对象。通过分析处理纤维分散沉淀图像(图2)，标定分散不均匀的纤维，通过对比疵点纤维根数或疵点所占图像像素点个数来反映不同工艺参数下纤维分散程度的优劣［27，38-40］。虽然纤网疵点的表征方式应用很多，但有时被认为仅仅是关注疵点而非纤网本身的均匀分布［41］，所以也存在一定的争议性。

2.5 样方分析

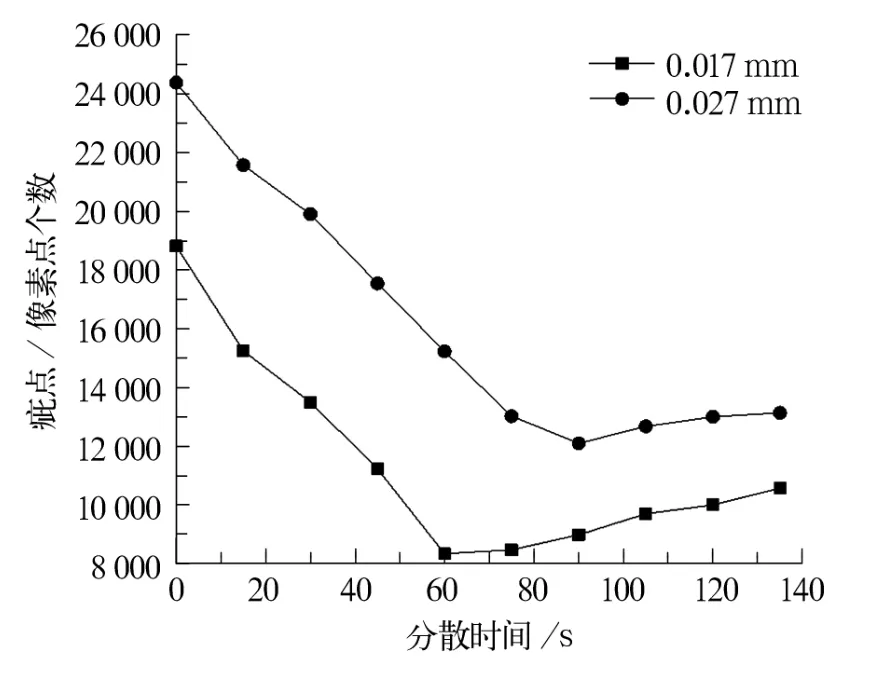
图2 分散时间对不同纤维直径形成疵点的影响

样方分析是一种空间点格局分析方法，通过将一组样方(通常是正方形单元格)覆盖在研究区域上，统计单元格中的点数并计算样方个数及频率，然后与完全随机过程对比来判断点模式的空间分布特征，用方差均值比VMR来判断［42-43］。样方分析法也具有一定的局限性，其与样方尺寸和分布类型具有密切的关系，改变样方尺寸的大小及形状可能会改变分布的判定结果［44］。

样方分析常应用于地理学、生态学和医学等领域［45-48］，也有纺织领域研究人员在样方分析的基础上添加一些算法推导出均匀指数、分散指数等指标［49-51］，进一步量化纤维的分散均匀程度并取代原本的VMR值，为各种不同参数条件下的纤维分散表征提供便利。例如将样方覆盖在纤维成网图像上，纤维在每一个样方中所占面积算成一个子集，统计每一个子集并计算其CV值，通过不同参数下CV值的大小来表征纤维的分散程度［41］，纤维分布越均匀，同一样方尺寸下CV值越低(图3)。

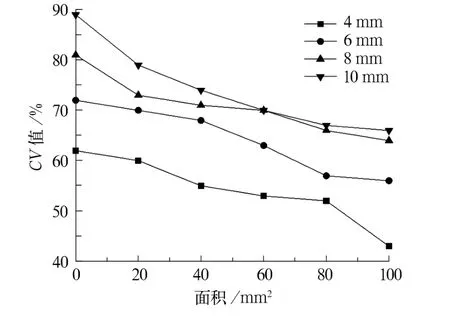
3 纤维长度在不同样方尺寸下的CV值变化

3 结语

湿法非织造布加工方法在非织造领域中起步较晚，但在原料要求、生产速度和产品特点上具有独特的优势，在近几年逐渐受到青睐。虽然湿法工艺源自于造纸行业，但在原料、加工工艺及设备要求上与其有一些差别。目前针对湿法工艺各个流程的研究较少，导致国内现有的湿法非织造布产品多采用纤维素纤维或植物纤维制成可冲散材料，而与国外各类合成纤维制成的屏蔽布、手机底板基布等通信材料应用相比尚存在较大差距。本文仅起到抛砖引玉的作用，希望能给其他行业和湿法非织造行业研究起到一定的帮助作用。

［1］张运展，苏求风，周庆乐.造纸工艺学［M］.北京：中国轻工业出版社，1999：1-12.

［2］张美云，宋顺喜，陆赵情.合成纤维湿法造纸的研发现状及相关技术［J］.中华纸业，2010(23)：49-52.

［3］KEREKES R J，SCHELL C J.Characterization of fibre flocculation regimes by a crowding factor［J］.Journal of Pulp and Paper Science，1992，18(1)：J32-J38.

［4］张洪涛，李友明，胡健.对纤维聚集因子求算公式的探讨［J］.纸和造纸，2001(2)：66.

［5］张曾，胡健.纤维分散性的评价［J］.造纸科学与技术，2001(5)：30-31.

［6］KEITH James M.Dispersion of synthetic fibers in wetlay nonwovens［J］.Tappi Journal，1994，77(6)：207-210.

［7］胡健，王宜，曾靖山，等.芳纶纸基复合材料的研究进展［J］.中国造纸，2004(1)：51-54.

［8］余调娟，李荣年，李红祝，等.聚丙烯纤维亲水改性技术及其应用［J］.中国造纸，2006(9)：6-8.

［9］唐爱民，张宏伟，陈港，等.改性涤纶纤维的抄造性能研究［J］.中国造纸，2003(8)：19-22.

［10］王进喜，王存增，刘文琪.造纸用化学纤维的表面亲水化处理［J］.中国造纸，2008(6)：64-67.

［11］胡志军.碳纤维的表面处理与成纸导电性能［J］.纸和造纸，2009(12)：18-22.

［12］SHIFFLER D A.Characterizing the dispersion kinetics of synthetic fibers in water［J］.Tappi Journal，1985，68(8)：88-91.

［13］RAMASUBRAMANIAN M K，SHIFFLER D.A computational fluid dynamics modeling and experimental study of the mixing process for the dispersion of the synthetic fibers in wet-lay forming［J］.Journal of Engineered Fibers and Fabrics，2008，3(1)：11-20.

［14］JAKUSH E A.Dispersants in wet laid glass mat theory and practice［C］.Tappi Proceedings，Nonwoven Conference，1991：163-172.

［15］高振宇.纤维悬浮湍流场中纤维运动扩散系数的研究［D］.杭州：浙江大学，2008：1-10.

［16］张志超.纤维悬浮流中两纤维直接相互作用的数值模拟［D］.杭州：浙江大学，2002：4-12.

［17］TORNBERG A K，GUSTAVSSON K.A numerical method for simulations of rigid fiber suspensions［J］.Journal of Computational Physics，2006，215(1)：172-196.

［18］WILHARM Madelynn T.The selection，application and function of whitewater chemicals in the wet lay process［C］.1992 Nonwovens Conference，1992：237-243.

［19］胡志斌，谢来苏.PEO-造纸用分散剂的应用研究［J］.西南造纸，2000(5)：9-10.

［20］杨斌，张美云，陆赵情.PEO分散芳纶纤维及分散机理研究［J］.纸和造纸，2012(6)：42-45.

［21］黄俊彦，杨汝男，邢效功，等.涤纶纤维绝缘纸用分散剂的研究［J］.绝缘材料通讯，1998(5)：18-20.

［22］黄睿.芳纶1414纸基功能材料及其增强技术的研究［D］.西安：陕西科技大学，2012：5-12.

［23］赵君，胡健，梁云，等.碳纤维表面特性及其在水中的分散性［J］.中国造纸，2008(5)：15-18.

［24］陈二龙，张淑萍.中长玻璃纤维分散用悬浮助剂的研究［J］.纤维复合材料，1997(2)：6-9.

［25］周雪松，王习文，胡健，等.芳纶纤维分散性能的研究［J］.造纸科学与技术，2004(6)：46-49.

［26］程隆棣.陶瓷纤维湿法非织造流浆中的分散性能研究［D］.上海：东华大学，2002：89-92.

［27］王闯，李克智，李贺军.短碳纤维在不同分散剂中的分散性［J］.精细化工，2007(1)：1-4.

［28］李涛，张美云.对位芳纶纤维纸的增强工艺［J］.纸和造纸，2011(4)：28-30.

［29］黄彩霞，陈慧文，李倩钰，等.剑麻纤维湿法抄造的分散性研究［J］.造纸科学与技术，2012(6)：32-35.

［30］吴士铮.造纸纤维的絮聚趋势［J］.国际造纸，1987(1)：20-24.

［31］JAYACHANDRAN A.Fundamentals of fiber dispersion in water［D］.North Carolina：North Carolina State University，2001：3-4.

［32］天津大学物理化学教研室.物理化学：下册［M］.北京：高等教育出版社，1993：621-631.

［33］胡海旭，陈学政，王羽，等.动电电位的测试在煤泥水治理中的应用［J］.环境保护科学，2001(2)：14-15.

［34］黄一磊，胡健，郑炽嵩，等.ζ电位对玻璃纤维分散的影响［J］.造纸科学与技术，2004(1)：31-33.

［35］JEONG S H，KIM S H，HONG C J.The evaluation of evenness of nonwovens using image analysis method［J］.Fibers and Polymers，2001，2(3)：164-170.

［36］SMITH James H.Use of a formation analyzer to evaluate the performance of additives used in the wet-laid process［C］.1991 Nonwovens Conference，1991：231-239.

［37］ROBERT J Wagner.Uniformity measurement of wet laid nonwovens using an image analyzer［C］.1993 Nonwovens Conference，1993：77-86.

［38］LATIFI M，TAFRESHI H V，POURDEYHIMI B.A note on an optical method to evaluate fiber dispersion in wet-laid nonwoven process［J］.Textile Research Journal，2008，78(6)：518-523.

［39］FATHI-KHALFBADAM S，LATIFI M，SHEIKHZADEHNAJAR S， et al. Analysis and simulation of fiber dispersion in water using a theoretical analogous model［J］.Journal of Dispersion Science and Technology，2011，32(3)：352-358.

［40］SAFAVI A，FATHI S，BABAEI M R，et al.Experimental and numerical analysis of fiber characteristics effects on fiber dispersion for wet-laid nonwoven［J］.Fibers and Polymers，2009，10(2)：231-236.

［41］DAS D，BUTOLA B S，RENUKA S.An investigation into fiber dispersion behavior in water with reference to wet-lay nonwoven technology［J］.Journal of Dispersion Science and Technology，2012，33(8)：1225-1232.

［42］黄芳.空间统计学及其在空间模式分析中的应用［D］.武汉：华中师范大学，2005：1-9.

［43］潘竟虎，靳学涛，韩文超.甘谷县农村居民点景观格局与空间分布特征［J］.西北大学学报：自然科学版，2011(1)：127-133.

［44］陈永刚，汤孟平，施拥军，等.样方形状对空间点格局的性能影响分析：以天目山阔叶林为例［J］.地理研究，2012(4)：665-671.

［45］WIEGERT R G.The selection of an optimum quadrat size for sampling the standing crop of grasses and forbs［J］.Ecology，1962，43：125-129.

［46］PAPANASTASIS V P.Optimum size and shape of quadrat for sampling herbage weight in grasslands of northern Greece［J］.Journal of Range Management，1977，30(6)：446-448.

［47］BRUMMER J E，NICHOLS J T，ENGEL R K，et al.Efficiency of different quadrat sizes and shapes for sampling standing crop［J］.Journal of Range Management，1994(1)：84-89.

［48］李仁杰，郭风华，张军海，等.北京市健身俱乐部多尺度空间格局［J］.地理科学进展，2010(2)：232-240.

［49］YAN Z，BRESEE R R.Flexible multifunction instrument for automated nonwoven web structure analysis［J］.Textile Research Journal，1999，69(11)：795-804.

［50］POURDEYHIMI B，KOHEL L.Area-based strategy for determining web uniformity［J］.Textile Research Journal，2002，72(12)：1065-1072.

［51］CHHABRA R.Nonwoven uniformity-measurements using image analysis［J］.International Nonwoven Journal，2003，12(1)：43-50.