基于ARIMA-GARCH模型的生育率随机预测

封铁英，罗天恒

（西安交通大学a.公共政策与管理学院；b.社会保障统计与精算研究中心，西安 710049）

0 引言

生育率是度量一个国家或地区时期生育水平最常用的可靠指标[1]。1992年以来，中国生育率的变化具有时间和空间维度上的压缩性特征，经历了从生育率水平由高到低的快速转变，且实施了无区域差别的生育干预政策。随着计划生育政策效应逐步显现，育龄妇女生育率长期稳定保持在更替水平2.1以下。根据第六次人口普查的数据，2010年中国妇女的总和生育率仅为1.19，十年内人口年平均增长率仅为0.57%，比1990～2000年年均1.07%的增长率下降了0.5个百分点。由于负增长惯性作用的影响，持续的低生育水平极有可能使中国陷入“低生育率陷阱”[2]。当总和生育率一旦降到1.5以下时，将引发低生育率的自我强化机制，从而进一步降低生育率，使生育率提高变得更加困难[3]。为了有效规避由此引发的一系列社会风险，不断深化对人口变动规律的客观认识、正确制定人口发展战略规划，选取较为准确的生育率数据、科学的评估和预测方法，准确预测人口生育率至关重要。

本文依据2010年第六次人口普查数据和历年的抽样调查数据，针对总和生育率的随机性特征，综合应用三随机预测方法[4]，以误差项白噪声假设和异方差假设为基础，基于ARIMA-GARCH模型对生育率进行误差外推，估计其未来值与预测区间，并进一步验证其有效性。

1 理论模型

1.1 随机过程

生育率序列具有强随机波动性，分析其随机过程的特性，是模型选择和有效拟合的重要基础。假设生育率是以时间为标号的一组随机序列Z(ω，t)，其中ω属于年龄组构成的集合，t属于时间集。对于特定的年龄组ω，Z(ω，t)是时间t的函数，称之为样本函数或实现。对生育率所有可能实现的全体称为随机过程。

定义(1)：设{Z(t)，t≥0}为随机过程,若对任意常数 τ、正 整 数 n 和 t1，t2...，tn∈T 、t1+τ，t2+τ...tn+τ∈T ，(Z(t1)，Z(t2)，...，Z(tn))与 (Z(t1+ τ)，Z(t2+τ)，...，Z(tn+ τ))具 有相同的联合分布，则称该随机过程{Z(t)，t≥0}为严平稳过程，也称狭义平稳过程.

定义(2)：对随机过程{Z(t)，t≥0},如果{Z(t)，t≥0}是二阶矩过程，对任意 t∈T，mZ(t)=EZ(t)=常数 ，对任意ω，t∈T ，RZ(ω，t)=E[Z(ω)Z(t)]=RZ(ω-t)，则称该过程{Z(t)，t≥0}为宽平稳过程，简称平稳过程。

显然，广义平稳过程不一定是严平稳过程，反之，严平稳过程只有当其二阶矩存在时方为广义平稳过程，但对于一个正态过程而言，二者是相同的[5]。在时间序列中，独立的随机序列通常是不存在或没有意义。生育率序列不是简单的独立同分布过程，很难给出其分布函数，其不确定性相对于金融数据更弱且趋势稳定，因此生育率随机过程分析通常使用弱意义下的平稳性——宽平稳。

1.2 自回归求和移动平均（ARIMA）模型

分析平稳时间序列一般应用ARMA模型，而对于非平稳的随机过程，则需要建立一种齐次非平稳时间序列模型——自回归求和移动平均模型（ARIMA）。经过适当的差分，齐次非平稳时间序列可转化为平稳的时间序列，即为ARIMA过程。不考虑季节性因素的ARIMA(p，d，q)模型的基本形式是：

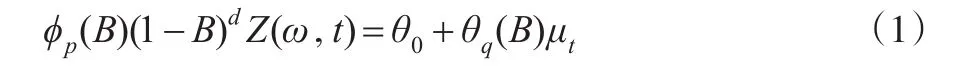
其中，平稳自回归AR算子φp(B)=1-φ1B-...-φpBp和可逆的移动平均MA算子θq(B)=1-θ1B-θqBq没有公因子，序列{μt}是服从同方差的高斯白噪声分布。参数θ0对于d=0和d＞0具有不同的作用。当d=0时，过程是平稳的，可知 θ0与过程的均值有关，即 θ0=α(1-φ1-...-φp)。当d＞0时，θ0被称为确定性趋势项，除非需要，θ0常常可忽略不计。由公式（1）得到的齐次非平稳时间序列模型即为ARIMA模型[6]。

ARIMA模型化过程的主要包括了模型识别、参数估计、诊断检验和模型预测四个步骤。根据样本的自相函数（ACF）和偏自相关函数（PACF）判断拖尾和截尾阶数，识别出若干可能模型，如 AR(p)、MA(q)、ARI(p，d)、IMA(d，q)或ARIMA(p，d，q)。为了比较模型的拟合效果，根据BIC法则和实践经验对模型进行诊断检验，BIC的值越小、平稳的R2越大，表明模型拟合效果越好，最终可从多个可能模型甄选出拟合效果最优模型，从而实现时间序列的模型化和预测。

1.3 广义自回归条件异方差（GARCH）模型

GARCH（p,q）模型的一般形式为：

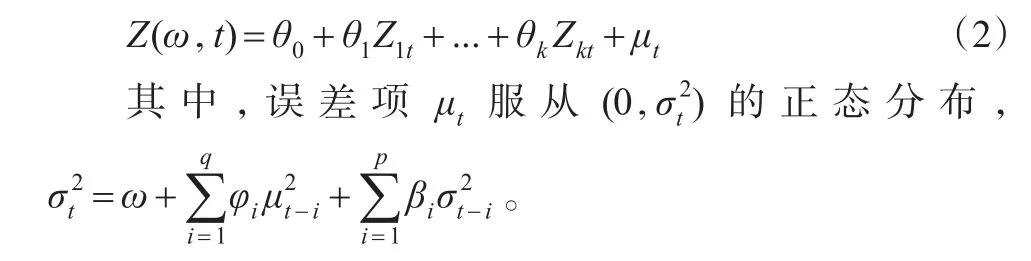
时间序列的GARCH(p，q)建模，首先进行GARCH（即异方差）效应检验，平稳序列的条件方差为常数值时，即不存在异方差效应时，不必建立GARCH模型；当存在异方差效应时，需建立GARCH模型并估计模型参数，最小二乘法最为常用，对于联合分布形式已知的时间序列，极大似然估计法更为精确；最后根据AIC准则，确定模型阶数并进行模型预测。由此可避免异方差效应对时间序列建模的冲击，并延长时间序列模型的预测长度。

1.4 ARIMA-GARCH模型

由于经济、社会、文化、政策及生物学规律、自然灾害等多重因素的影响，生育率序列具有极强的不确定性。仅仅假设生育率随机过程平稳的模型拟合可能是不合适的，应当根据其随机特性筛选最优模型。ARIMA-GARCH模型正是基于误差项分布的同方差和异方差分布的不同假设，在随机过程分析的基础上，按平稳序列建模方法构建生育率的ARIMA(p，d，q)模型并检验序列的异方差效应，以决定是否建立 GARCH(p，q)模型对 ARIMA(p，d，q)的预测误差项进一步建模，最终实现生育率的有效随机预测。

（1）生育率随机过程分析

根据序列图初步判定生育率原始序列的趋势性、波动性和季节性特征，而后通过原始序列的统计指标（均值、中位数、偏度、峰度等）确定该随机过程的分布状态，最后在样本自相关函数（ACF）及偏自相关函数（PACF）的截尾和拖尾特性的基础上判断序列属于平稳或非平稳过程。

（2）平稳序列转化与ARIMA建模

对于存在明显趋势和强随机波动性的序列，应考虑通过适度差分将非平稳序列转化为平稳序列，在残差序列{μt}服从同方差分布假定下，应用ARIMA模型对随机过程建模。大量实践经验证明，生育率随机过程的ARIMA模型构建应当同时考虑变量自回归部分（AR(p)）和残差移动平均（MA(q)）部分，建立 ARIMA(p，d，q)模型拟合生育率随机过程的效果可能较好。

（3）异方差效应检验与GARCH建模

为了控制生育率预测模型残差项可能存在的相关性，需要检验残差项的异方差效应并建立GARCH模型，GARCH模型的建立，有效解决了ARIMA模型对误差项异方差性的忽视，降低由此引发的重要细节信息损失，从而能够更准确地反应生育率的随机变动趋势并提高预测的置信度。在ARIMA(p，d，q)模型计算出残差序列后，构建残差平方序列，并计算平方序列的自相关函数（ACF）和偏自相关函数（PACF），以检验残差平方和是否遵循自回归（AR）模型形式，从而得出是否存在异方差效应的结论。如果异方差效应是存在的，则应该建立误差项的GARCH模型；如果异方差效应不存在或是在可以接受的范围内，则没必要建立GARCH模型。过度模型化的结果可能导致计算复杂性，对预测准确性的改善微乎其微，因此建立残差项的GARCH模型应当是审慎的。

2 模型应用

根据2010年全国第六次人口普查和历年人口统计年鉴相关数据，本文选取1949～2010年总和生育率数据作为样本集，基于ARIMA-GARCH模型建立生育率随机预测模型，以SPSS 20.0及EVIEWS 6.0为平台，实现总和生育率的随机预测并检验模型的预测效果。

由原始序列图（见图1）分析可知，1949～1988年，中国总和生育率的不规则变动明显，出现急剧降低和快速增长的短期变动以及小幅度不规则的中长期变动，1988年之后，生育率缓慢平稳降低，表明受自然灾害、计划生育政策、社会文化变迁等因素的影响，中国生育率总体呈现显著下降趋势并存在较强随机波动性（见图1）。在观测原始序列的基础上，为了准确描述总和生育率的随机波动特征，进一步分析其统计特征：偏度（Skewness）为0.4015，存在明显的右偏趋势，而均值（Mean）为2.3876，序列不服从正态分布；峰度（Kurtosis）为1.8347，低于正态分布的峰度值3，“尖峰”特征不明显。显然，对于非正态分布的总和生育率原始序列，满足“厚尾”特征，但“尖峰”特征不明显。因此，对中国总和生育率序列，初步假定生育率数据是平稳时间序列，或者经过适当差分将非平稳时间序列转变成平稳时间序列，建立生育率的ARIMA模型。GARCH建模时则应首先检验是否存在异方差效应，从序列的峰值和偏度值来看，初步认为异方差在可以接受的范围内，是否需要建立GARCH建模应当进一步检验。

图1 1949～2010年中国总和生育率序列

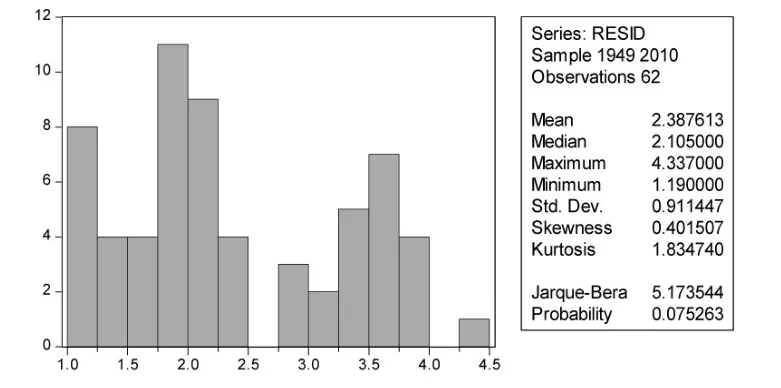
图2 1949～2010年中国总和生育率频数图与统计特征

生育率ARIMA模型构建过程中，首先将原始数据进行对数变换，以弱化其随机波动影响。对数变换后的生育率序列具有向下趋势，因此考虑将变换后的序列进行一阶差分，使其平稳化。应用ADF单位根检验一阶差分后序列的平稳性，检验统计量为-6.4554，其P值比显著性水平α为0.05的序列趋于平稳（见表1），表明原始序列的一阶差分是合适和必要的。一阶平稳的生育率序列的AR(p)和MA(q)阶数可通过自相关函数（ACF）和偏自相关函数（PACF）识别。由检验结果（见图3）可知，ACF在滞后1期，PACF在在滞后2期出现较大衰减。因此，生育率序列的 ARIMA(p，d，q) 模 型 可 以 考 虑 ARI(2,1)、IMA(1,1)或ARIMA(2,1,1)模型，根据多个模型检验结果（见表2）对比分析可知，ARIMA(2,1,1)模型的 R2最大（0.149）且BIC值最小（-2.181），表明ARIMA(2,1,1)模型对于总和生育率序列的拟合效果优于ARI(2,1)、IMA(1,1)模型。

表1 总和生育率序列一阶差分后的ADF单位根检验

图3 一阶差分后总和生育率序列的ACF和PACF检验

由图4可知，ARIMA(2,1,1)模型残差序列{μt}分布不平稳，具有较强的随机性，未出现在某一段时间内集中分布的“集群”现象，异方差效应的直观显示不明显。为进一步检验残差的异方差性，计算残差平方，可以看出平方后的残差序列平稳，仅于1962年前后出现较大值，其他时间段内序列在0～0.1的范围内小幅波动。序列的ACF和PACF检验结果（见表3）表明，自相关系数和偏自相关系数均显著为0，且p值均大于0.05，对总和生育率残差异方差假设未通过检验，可见总和生育率的异方差效应是不显著的，不需要再通过GARCH对模型残差进一步建模。

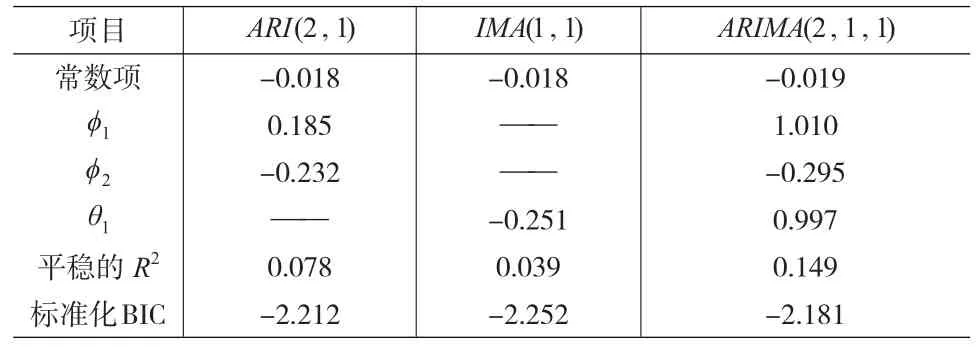
表2 总和生育率ARIMA(p,1,q)模型检验结果

对于异方差效应不显著的中国总和生育率序列的随机预测，仅需应用ARIMA(2,1,1)模型。经过适当差分实现序列的平稳化，考虑自回归部分AR(p)和移动平均部分MA(q)更符合总和生育率的现实状况。

图4 ARIMA(2,1,1)模型残差和残差平方分布

表3 ARIMA(2,1,1)模型残差平方和的ACF和PACF检验

本文以第六次全国人口普查（2010年）的总和生育率数据为基础，预测中国未来30年的生育率及其变动趋势（见图5）：在90%的估计区间内，2010～2040年生育率将从1.8左右缓慢下降并持续保持低于1.5的超低生育率水平。在未采取有效的生育率干预情况下，长期的低生育率将会成为一个不可避免的现实，随之出现的“生育陷阱”有可能会成为困扰中国人口正常增长的障碍。与假定生育政策维持现状不变、完全取消、适度放松管制的三种政策环境下的场景预测[7]或高、中、低方案的确定性预测不同，ARIMA-GARCH模型完全根据历史数据的变动规律预测未来趋势，无主观干涉，可得到估计值的置信区间，预测结果更为科学、可信。与朱勤[8]对2000～2010年分年龄生育率模拟推算相类似，本文生育率预测采用纵向的时间序列数据，建立生育率的模拟和仿真模型，区别在于对总和生育率的分析是否是基于队列生育率。由于分年龄的生育率数据缺失，以及累积的分年龄生育率模型误差[9]，年龄别生育率模拟预测期间短，直接运用总和生育率数据进行生育率随机预测更为有效。

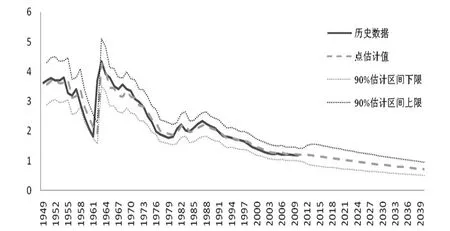
图5 1949～2010年中国总和生育率历史数据、估计值与估计区间

3 结论与建议

针对传统确定性预测方法的固有缺陷和生育率的随机波动特征，本文提出基于随机理论和时间序列分析的生育率随机预测ARIMA-GARCH建模与仿真方法。以中国总和生育率为例，通过对生育率序列随机过程分析，辨识序列的平稳特性和不规则变动程度，为模型拟合和参数选择提供支持；根据生育率时间序列属性，构建自回归求和移动平均（ARIMA）模型，将原始数据函数化；对于生育率时间序列的自相关性和异方差效应，构建广义自回归条件异方差(GARCH)模型对其进行检验并建模，有效延长了ARIMA模型的预测长度并提高预测精度。相对于其他生育率随机预测方法，本文基于历史数据随机特性构建的ARIMA-GARCH模型能够准确地反映时间序列的动态变化过程，避免原始序列重要的细节信息损失，为生育率预测提供了一种新的视角和途径。

基于ARIMA(2,1,1)-GARCH随机预测模型的生育率估计结果表明：在90%的置信区间内，未来30年，中国妇女的总和生育率从2010年的1.19下降到2040年的（0.4787～0.9997）的区间内。基于研究结论，本文提出应对中国生育率持续走低的对策建议：

（1）警惕“低生育陷阱”，防止“超低生育率”

中国的生育率从1990年之后开始低于2.1的人口更替水平并持续降低，到2040年左右，生育率水平极有可能达到1.0以下的“超低生育率”[10]。20世纪60年代中期，西北欧部分国家的总和生育率在降到更替水平之后持续下滑，由此导致人口负增长。根据低生育率陷阱理论，小于1.5的总和生育率存在“自我强化机制”，导致生育率难以重新提高。生育率水平下降带来的后果可能是严重的，尤其是在“人口红利”后期，以劳动密集型模式为主的经济发展与生育率降低、劳动者素质上升的社会现实相脱节，导致了我国“民工荒”与大学生“就业难”并存的矛盾现象[11]。中国应当对生育率的持续降低保持高度警惕，采取有效措施来缓解生育水平的下滑风险。

（2）适时调整生育政策，逐步释放人口增长空间

2013年11月15日，十八届三中全会的《中共中央关于全面深化改革若干重大问题的决定》提到“坚持计划生育的基本国策，启动实施一方是独生子女的夫妇可生育两个孩子的政策”。单独二胎政策是对计划生育政策的适度调整，释放出了生育政策改革的积极信号。根据联合国2012年度发表的生育率预测，中国同韩国、日本、欧美等国家和地区妇女平均生育低于更替水平并将继续下降。有学者指出，即使是没有独生子女政策，中国的生育率也仅在2.0左右。生育率转变有其自然的规律，同为中华文化圈的韩国，在经历生育率下滑到1.7时提出鼓励生育，但是生育率仍然持续下降。对中国而言，2010年人口普查时生育率水平仅为1.19，人口数量的减少伴随着“人口红利”的消失、结构老龄化严重、出生性别比偏高等现实问题同步出现，调整生育政策势在必行，应通过建立生育成本补偿机制等多项、全方位配套措施，逐步释放人口增长空间，促进人口、资源、环境的可持续协调发展。

[1]高爽，陈卫.论内在总和生育率[J].人口与经济,2013,(1).

[2]石人炳.低生育率陷阱：是事实还是神话[J].人口研究,2010,34(2).

[3]Lutz W,Skirbekk V,Testa M R.The Low-Fertility Trap Hypothesis:Forces That May Lead To Further Postponement and Fewer Births in Europe[J].Vienna Yearbook of Population Research,2006，(4).

[4]Hyndman R J,Booth H.Stochastic Population Forecasts Using Functional Data Models for Mortality,Fertility and Migration[J].International Journal of Forecasting,2008,24(3).

[5]李锦华，陈水生.非高斯随机过程模拟与预测的研究进展[J].华东交通大学学报,2011,28(6).

[6]魏武雄，易丹辉，刘超等译.时间序列分析：单变量和多变量方法[M].北京：中国人民大学出版社，2009.

[7]王焕清.不同计划生育政策下的我国人口预测研究[J].统计与决策，2013,(5).

[8]朱勤.2000～2010年中国生育水平推算——基于“六普”数据的初步研究[J].中国人口科学,2012,(4).

[9]郭志刚.再论队列平均子女数不能作为当前总和生育率的估计[J].中国人口科学，2008,(5).

[10]马小红.“双独政策”影响下北京市人口生育水平变动分析[J].人口研究，2004,(1).

[11]翟振武，赵梦晗.生育率下降与经济发展模式转型[J].人口与经济，2013,(1).