数学模型的教学实践与思考

【摘 要】 “数学模型，乃是针对或参照某种事物系统的特征或数量相依关系，采用形式化的数学符号和语言，概括地或近似地表述出来的一种数学结构。”教学中，我们既要让学生深度理解模型的意义，灵活转换现实问题与数学模型；也要让学生从模型的算术意义走向代数意义，培养学生的早期代数思维；更要带着学生体会模型的发展变化过程，理解数学发展的本质，这样才能够充分实现数学模型的教学价值。

【关 键 词】 转换；代数意义；拓展

【作者简介】 陈晶，江苏省南通崇川学校，中小学一级教师，研究方向：小学数学教学的理论与实践研究。

“数学模型，乃是针对或参照某种事物系统的特征或数量相依关系，采用形式化的数学符号和语言，概括地或近似地表述出来的一种数学结构。”“广义地讲，数学中的各种基本概念和基本算法，都可以叫做数学模型。加减乘除都有各自的现实原型，它们都是以各自相应的现实原型为背景抽象出来的。”从这个意义上来看，“建立数学模型可以帮助学生从数量关系的角度更准确、更清晰地认识、描述和把握现实世界。”在教学过程中，如何让学生深度理解数学模型的意义，提高学生运用数学模型解决问题的能力，把握数学模型发展的核心要素，并且根据已有的经验再生出新的数学模型，充分发挥数学模型的教学价值呢？笔者以苏教版二年级上册“乘除法意义的复习”为例谈谈自己的教学实践与思考：

一、灵活转换，理解数学模型的意义

乘法和除法的数学模型，用字母表示分别为：a×b=c（a≠0 ，b≠0），c÷a=b，c÷b=a，在第一学段的教学过程中，我们也常常描述为：每份数×份数=总数，总数÷每份数=份数，总数÷份数=每份数。从这些表达式可以看出：对于模型的运算意义以及模型所对应数量的理解是学生理解乘法和除法模型的关键。在教学中，通过以下两个过程，让学生深度理解乘法和除法的模型：

1. 模型之间合理转换，理解模型的运算意义。通常把乘法定义为 “求几个相同加数的和的简便运算” ，把除法定义为“已知两个因数的积与其中的一个因数，求另一个因数的运算”。从这两个定义可以看出，加法运算是乘法运算的基础，乘法运算是除法运算的基础。在教学过程中，通过以下三个层次的学习让学生对模型进行灵活转换，深度理解乘法和除法模型的运算意义：

第一层次，让学生看图（如图1）提出一个用加法计算的实际问题（如图2），然后把加法计算的实际问题转换成减法计算的实际问题（如图3），在此基础上，揭示加法模型和减法模型的意义以及两者之间的关系（如图4）。

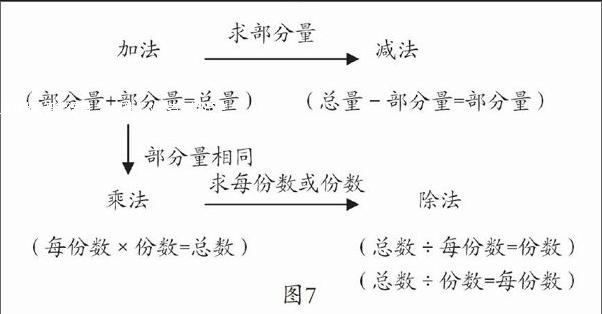
第二层次，让学生改变其中一个盘子里苹果的个数，变成一道乘法计算的实际问题（如图5），理解乘法的意义。再把乘法计算的实际问题转换成除法计算的实际问题（如图6），理解除法的意义。最后，揭示乘法模型和除法模型的意义以及两者之间的关系（如图7）。

第三层次，在前面理解了乘法模型和除法模型的运算意义以及它们之间的关系后，再引导学生比较：除法和减法之间有什么关系？让学生理解其中的两点：其一，减法就是求加法算式的“部分量”问题，除法也就是求乘法算式中的“每份数”或“份数”的问题，减法运算和除法运算产生的思维方法是相同的；其二，除法也可以转换成部分量相同的减法，即可以借助于部分量相同的减法来计算除法，体会到两类运算之间的关联。

上述过程中，通过更换情景图中的数据，把加法运算转换成乘法运算，理解乘法运算的意义以及加法运算和乘法运算之间的关系；通过把乘法运算转换成除法运算，理解除法运算的意义以及乘除法之间的互逆关系；通过两类互逆关系的比较，体会到产生减法运算与除法运算思维方法之间的关联。上述转换与比较，让学生深度理解了乘法模型与除法模型的运算意义，打通了加减乘除四类运算之间的联结。

2. 数学模型与实际问题转换，丰富模型的现实意义。在学生理解了乘法和除法模型的运算意义后，还需要丰富模型的现实意义，达到对模型里“每份数”、“份数”和“总数”的深度理解，这样才能主动运用数学模型解决问题。在教学中，主要安排以下两个层次的学习：

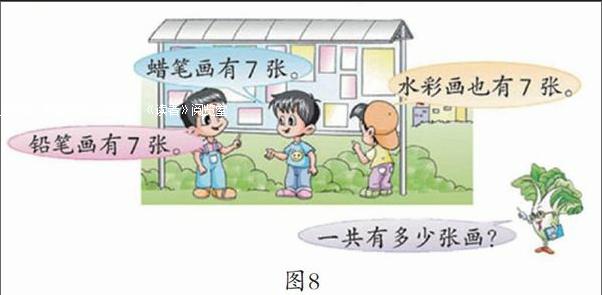
第一层次，根据实际问题确定相应的数学模型。在解决实际问题的时候，让学生根据实际问题中的数量找到对应模型里的“每份数”、“份数”和“总数”，然后确定解决问题的思路。在解决乘法计算的实际问题（如图8）时，引导学生思考：“每人有7张画片”是“每份数”，“有3人”是“份数”，求“一共有多少张”就是求“总数”，可以利用“每份数×份数=总数”来解决问题。除法的实际问题也可以借助于同样的方式进行思考。

第二层次，基于数学模型找到现实生活中的问题。除了在解决实际问题的过程中，让学生主动把实际问题与数学模型进行对接，还可以引导学生基于数学模型，找到现实生活中的问题，加深对“每份数”、“份数”和“总数”的理解。如教学过程中，可以让学生根据“每份数×份数=总数”这样一个数学模型，编出相应的实际问题。

通过上述两个层次的转换练习，理解实际问题数量之间的本质联系，丰富数学模型的表征，打通数学模型与实际问题之间的思维通道，理解数学模型的价值，提高学生运用数学模型解决问题的能力。

二、横向拓展，从数学模型的算术意义走向代数意义

在学生理解了乘法模型与除法模型的意义后，还需要进一步拓宽模型的内涵，引导学生从模型的算术意义走向代数意义。以“每份数×份数=总数”这个模型为例，如果已知“每份数”和“份数”，求出“总数”，运用这个模型来解决问题，则是基于这个模型的算术意义；如果已知“总数”和“每份数”，求“份数”，运用这个模型来解决问题，则是把未知量与已知量放在同等的地位参与运算，是运用方程解决问题的雏形；如果已知“总数”，让学生去寻找“每份数”和“份数”，则是反比例函数“y=- （k∈R且k≠0）”的雏形，上述后者两项内容均超越了模型的算术意义走向了模型的代数意义。在学习过程中，通过创设合适的问题情境，引导学生从模型的算术意义走向代数意义，加深对模型意义的理解，培养学生的早期代数思维。endprint