巧设认知冲突 促进有效思维
2015-01-14袁志芬
袁志芬
数学新课标明确指出,要转变“授——受”的单一教与学的模式,发挥学生的主体性,使学生主动参与数学活动,自主探究交流,合作学习,促进有效思维。笔者认为,巧设有效的认知冲突,是提升学生思维的必要路径,也是有效路径。在教学中,教师不断制造认知冲突,能够使学生从不平衡到平衡,再从平衡到不平衡,循环往复,获得对知识的深入理解和实践运用,实现数学思维的有序提升。下面笔者根据自己的成功教例,谈谈体会。
一、悬念激趣,触发思维
小学生好奇心强,对未知的事物充满求知欲,这既是引发认知冲突的有利因素,又是触发思维的契机所在。教学中教师要善于挖掘教材,并结合教材特点、教学目标创设故事情境,设置认知悬念,激发学生兴趣,触发数学思维。
如教学苏教版二年级教材“认识厘米”时,为了让学生对“厘米”这一长度单位建立初步的应用意识,我特意在课始播放动画视频,创设“黑猫警长”的故事情境:黑猫警长抓住了盗窃珠宝的老鼠“一只耳”,据它交代,赃物就藏在大树正北方向7个脚长的地方。可是黑猫警长赶到那里,从大树开始向正北方向走了7个脚长,却始终都没有找到赃物所在。大家猜一猜,到底是一只耳在说谎还是警长的问题?学生经过讨论后认为,黑猫警长的7个脚长和一只耳的7个脚长距离并不相等,这是导致问题的直接原因。此时我创设认知冲突:如果生活中人人都用自己的长度标准来测量距离,将会制造很多麻烦。应该怎么办呢?学生认为,要用一个统一的长度来作为测量标准。此时我引入厘米这一长度概念,使课堂教学显得自然而然,水到渠成。
二、新旧结合,启发思维
新知犹如树的新枝,新枝必从旧枝生发而来,教学亦然。教师要善加挖掘,分析学生已有知识结构、经验,并与教材内容紧密结合,根据新旧知识的差异,在新知的生长处制造认知冲突,启发学生的思维。
如在教学苏教版二年级“确定位置”时,我采用“喜羊羊与灰太狼”的情境创设,出示横排竖排的一群羊儿,并做了这样的问题预设:“灰太狼伪装成羊儿,就隐藏在羊群中的第二个。你能找出来吗?”学生认为有两种情况,一种是从左往右数第二只,一种是从右往左数第二只,那么到底怎么才能找出来呢?由此学生得到认知,要想找到灰太狼,就必须要知道两个要素,一个是“第几个”,一个是数的顺序,从而学生得到确定位置的相关经验。那么是否确定了这两个要素就万无一失了呢?接下来我改变了问题的条件,出示小动物的做操方阵,让学生思考:现在灰太狼又伪装成小动物混在队伍中,知道它站在第三个,哪个才是它呢?这样一来,光知道“第几个”和“数的顺序”显然是不行的,经过思考和自主探究,学生发现除了确定第几个之外,还要确定第几排,但这个第几排的确定也需要一个条件,那就是数的顺序,到底是从前往后数还是从后往前数。
以上教学中,我根据教材内容进行整合设计,从学生已有经验出发,运用两个情境突破学生的旧知,先明确了“第几个”和“怎么数”,但在第二个情境中产生了矛盾,光知道第几个是不行的,还需要知道第几排。由此,学生通过新旧知识的嫁接,主动思考,认识到要知道“两个第几”才能解决问题,思维获得了启迪。
三、对比辨析,深化思维
在数学双基教学中,教师常常利用变式对比和反例进行概念教学。所谓变式,就是指针对知识的本质通过实例的不断变换,让学生明确属性,获得更深入的感知。而反例则是变换本质属性,让学生辨析对比,在认知冲突中巩固和深化认知,有效提升数学思维。
如在教学苏教版二年级“倍的认识”一课时,我创设这样的情境:小猫采到了6朵红色花和3朵黄色花,想一想,红色花和黄色花的数量有什么关系?学生认为红色花是黄色花的2倍。为什么这样呢?我让学生上台摆一摆、分一分,看看为何是2倍的关系。紧接着设置了变式:如果小猫采到8朵红花和4朵黄花,那么红花和黄花有什么数量关系呢?如果小兔采到4朵红花和2朵黄花,那么黄花和红花又是什么数量关系呢?学生由此对倍数关系有了较为直观的表象积累。
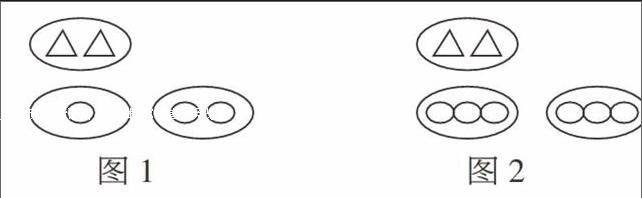
为了巩固“倍的认识”,我启发学生思考:为什么花的数量不同,但都是2倍关系呢?学生讨论后认为,上面的花是两份,下面的花是一份,由此得到2倍的关系。此时我呈现反例:如下图所示。
图1 图2
图中的椭圆形和三角形的数量关系也是2倍关系吗?为什么?学生从2倍关系的本质入手,认为两者的关系不是2倍关系。在图1中,是把2个三角形看做一份,一个椭圆形看做一份,另外2个椭圆形看做一份;在图2中,是将2个三角形看做一份,3个椭圆形看做一份。
以上教学中,通过反例和对比辨析,学生在认知冲突中学会主动比较共同点,对倍的意义有了深入理解,能够自主建构倍的概念,深化数学思维。
总之,在低年级数学教学中,创设有效的认知冲突,能够激发学生数学思维的有效提升,培养和发展数学能力,这无疑正是数学课堂教学的目标和本质所在。
(责编 罗 艳)endprint
