什么是计算教学的有力支撑?
2015-01-14张莹
张莹

“买文具”是北师版小学数学四年级上册“除法”单元第一课时“除数是整十数的除法”的教学内容,是学生后续学习“三位数除以两位数”笔算除法中试商、调商的重要基础,主要借助除数是整十数的除法,探索除数是两位数除法的计算过程,重点学习判断商是几位数(定位)的方法。在学习本课之前,我对学生进行前测:“你能计算出90÷30和100÷40的结果吗?可以的话,请用尽量多的方法计算出来。”结果从学生的错例中发现,学生对于商及余数意义的理解不够深刻,竖式计算也还存在一定的问题。很多教师提高学生计算能力的“法宝”是多练,而我认为让学生充分理解算理是教师在计算教学中最该下工夫的地方。与此同时,在教学实践过程中,我感到运用数学模型,引导学生进行不同算法间的对比沟通是切实可行的方法之一。
一、通过必要的追问,引导学生感知算理
师(出示主题图):淘气带了80元钱,每个书包20元,问能买几个书包?怎么列式?
生1:80÷20。
师:为什么要用除法列式?你是怎么想的?
生2:淘气带了80元钱,每个书包20元,用80÷20就是看80里面有几个20,也就是能买几个书包。
师:下面,请同学们用自己喜欢的方法表示出“80里面有几个20”。
……
除法有包含除和等分除两个重要模型,在此之前学生接触更多的是等分除,而本节课要让学生尝试用包含除的方法去理解算理。因此,在上述教学中,我没有满足于学生能正确列式就可以了,而是进行追问:“为什么要用除法列式?你是怎么想的?”在学生说出包含除的含义后,我引导学生的思维从列式计算转向了对算理的思考。
二、通过模型的支撑,引导学生理解算理
根据认知发展理论可知,四年级学生的思维以具体形象思维为主,再向抽象思维转化。因此,为符合学生的认知规律,丰富学生的感性认识,提高课堂教学的有效性,课上在学生遇到“80÷20”这样一个新知识点时,我为学生提供方格图、小棒、纸币等直观模型进行辅助教学,更好地帮助学生理解算理、掌握算法。学生操作的这些模型不仅是现在用来理解算理的工具,而且也是日后用以回忆本知识点和链接其他相关新知识的重要抓手,这些模型还将为实现算法多样化和发展学生的个性提供了支撑条件。学生的方法如下:
(1)20+20+20+20=80;
(2)80-20-20-20-20=0;
(3)因为8÷2=4,所以80÷20=4;
(4)20×( )=80,因为20×4=80,所以80÷20=4;
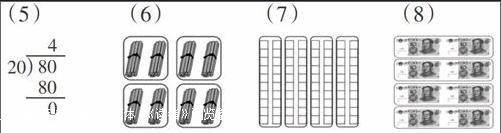
(5) (6) (7) (8)
■
在教学过程中,教师应关注学生的个性发展,积极创造条件让学生亲历建构数学模型的过程,并鼓励解决问题的策略和算法多样化,使不同层次的学生在课堂上都能有所得。
三、通过对比沟通,引导学生深化算理
无论是前测的结果显示,还是从课堂的实际情况来看,我发现学生在利用模型解决问题的过程中都没有出错,但用竖式进行计算时则有各种不同的错误出现。通过分析,我认为竖式计算的过程与学生摆小棒、分纸币和圈格子图所经历的思维过程其实是一样的,都是一个分的过程,然而学生的写竖式由于比模型更为抽象,同时缺乏横向的对比沟通,因此导致计算过程错漏百出。
1.不同算法间的对比沟通
如果教师只是为了让学生用模型而用模型,将模型操作与竖式计算当成两个不相干的活动,忽视两者之间的联系,那么“让学生亲历建模的过程,积累数学活动经验”就成了一句空话,模型在计算教学中存在的意义也会极大的下降。因此,为了提高课堂教学效率,较好地帮助学生降低学习抽象知识的难度,我引导学生对不同的算法进行对比沟通,逐渐形成具体模型与抽象算式之间的联系,使学生在计算时头脑中有直观模型作支撑。如课堂上,在学生把计算80÷20的各种方法在黑板上展示之后,我问学生:“刚才同学们用不同的方法计算出了结果,下面我们看看,大家都是在哪找到80的?”大部分学生都能顺利地找出80根小棒、80元钱、80个小方格和横竖式中的80。我继续追问:“这些不同地方的80,有什么联系?”学生回答:“表示淘气带了80元钱。”我继续引导学生找出20,很快学生也都找出了2捆小棒、2张10元钱、2列方格和横竖式中的20。我继续问学生:“20表示什么?”学生在我的引导下回答出了“表示一个书包20元钱”的正确答案。我乘势追问:“大家看看,4在哪?”在一生指黑板上横竖式中的4及圈出小棒图、方格图和钱币图中的4份后,我问道:“所有的这些4,其实都可以用来表示什么?”学生水到渠成地回答出:“表示可以买4个书包。”……在这个环节中,我通过不断的追问,引导学生进行不同算法之间的对比沟通,使学生在讨论和辨析中,逐步地感受到算法形式上的多样化和算理本质上的同一性。
2.不同错误间的对比沟通
在学习过程中,学生不可避免地会因为一些认知上的偏差,导致出现这样或那样的错误。这时教师不应简单地予以否定,而是让学生的思维过程得以充分展现,从中发现学生出现此类错误的原因,并加以针对性的指导,使学生的错误变成为课堂中宝贵的教学资源。因此,对于学生在学习过程中产生的错误,教师要有一定的预设性,并根据课堂上学生的实际情况,尽可能多地将各种错误和正确方法在同一时间内展现在学生面前,引导学生经历一个自我辨析、纠错、改正和提高的过程,从而有利于学生更加牢固地掌握所学的知识。如学生尝试独立完成80÷20的竖式计算时,我在课堂巡视中发现了以下四种竖式写法,于是将它们展示到黑板上。
(1) (2) (3) (4)
■
师:请大家仔细观察这些同学写的竖式,选择其中一个,说说你的想法。
生1:第(3)个竖式肯定不对,怎么可能商的个位上是空的,而十位上却有数字?个位上是空的表示没有,就要用0来占位,那么商就成了40,难道80里面有40个20吗?所以,我认为应该把4写在商的个位,这样才能表示80里面有4个20。
生2:我认为第(4)个竖式也不对。淘气带了80元钱,每个书包20元,最后的结果只能是买4个书包,而不是40个书包,所以商4应写在个位上。
生3:第(1)个竖式也不对,这里的商虽然是写在个位上了,可是被除数80下面的数应该是80,而不是8。
生4:第(4)个竖式下面写得也不对,因为它是除数和商相乘得到的,除数是20,商是4,20×4=80,所以应该是80,而不是8。
师:那你知道这个80表示的是什么意思吗?
生5:这里的80表示买4个书包共花了80元钱。
师:通过刚才的讨论,我们找到了正确的竖式,应该是——
生(异口同声):第(2)个算式!
……
上述教学中,学生出错后,我并没有急于指正或批评,而是把学生的各类错误和正确的写法放在一起,让学生在对比中进行自我辨析和自我纠错。这样,算理就在学生的互相讨论和质疑中越辩越明,算法也越辩越清。
通过本节课的教学,我感受最深的是,不仅仅要在计算教学中使用模型,还要加强模型与算式之间的沟通,形成方法间的对比,才能成为计算教学中的有力支撑,更好地帮助学生理解算理。总结本次教学,是在以学生发展为本、以学生为主体的教学理念下,通过追问感知、理解算理、对比沟通三个步骤,使学生对除数是整十数除法的算理有初步的认识和理解,并引导学生进行专门的练习和更进一步的算法纠正,从而实现预设的教学目标。
(责编 蓝 天)endprint
