城市匝道桥抗倾覆稳定性及实际通行能力研究

付兆华

（山西太旧高速公路管理有限责任公司，山西 太原 030006）

0 引言

独柱墩连续梁桥作为立交匝道桥梁，占用桥下空间小、整体结构美观，因此近年来在现行高速公路以及市政道路中的应用非常广泛[1]。但是这种形式的桥梁有其致命缺点即横桥向采用单支点支撑的方式，由于横向支点少在偏载作用下，对结构的抗倾覆稳定性极为不利，另外公路桥梁事业的发展速度较快，目前现行的公路桥梁规范中，涉及到桥梁倾覆稳定性的相关规定缺乏，为了保证桥梁整体稳定性，城市桥梁设计规范中虽提出了该设计要求，但未给出明确的计算方法和标准。

本文以某地区市政匝道桥为例，在结构分析的基础上，建立有限元模型对该桥梁的横向抗倾覆稳定性进行分析，根据程序计算结合行业中相关研究，对此类结构形式抗倾覆稳定性[2]计算方法进行验证，并根据该地区通行的实际重型车辆，进行实际通行能力研究。

1 工程概况

依托工程匝道桥位于立交第三联，圆曲半径为306.25 m，该联上部结构为3×30 m预应力混凝土连续箱梁桥，梁高1.6 m，箱梁顶板全宽9.5 m，翼缘板悬臂长 0.94 m，底板宽 6.86 m，悬臂端部厚0.15 m，根部厚0.3 m，顶板厚0.20 m，底板厚0.2～0.5 m，腹板厚0.35～0.6 m。该联伸缩缝所处桥墩处设置盖梁，盖梁高1.6 m，桥墩立柱采用1根直径1.5 m的圆柱，基础采用1.8 m厚承台，采用2根直径1.5 m桩基，桩长41～43 m；中墩处立柱采用1根直径1.5 m圆柱，基础采用1.8 m厚承台，采用2根直径1.3 m桩基，桩长48 m。

设计技术标准：该桥位于城市快速路，双向四车道，桥面设横坡1.5%，桥涵设计荷载等级为城-A级。

2 计算依据及假定

2.1 计算依据

分析桥梁结构在设计荷载作用下桥梁结构的抗倾覆能力时，依据《城市桥梁设计规范》（CJJ 11—2011）中关于桥梁设计荷载的取值。

现行规范中缺乏上部结构抗倾覆稳定性验算的相关规定，本文研究依据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（征求意见稿）中相关规定对依托工程的上部结构进行抗倾覆能量计算。计算工况参照浙江省公路管理局文件浙交路〔2009〕102号文《关于桥梁上部结构抗倾覆验算汽车荷载的规定》。

2.2 计算假定

a）主梁及桥墩有足够的强度，不会先于结构倾覆产生强度破坏。

b）主梁及桥墩有足够的刚度，不会先于结构倾覆产生失稳破坏。

c）桥台及桥墩支座为单向受压支撑。

d）不考虑支座支撑面积，假定支座为理想点支撑。

2.3 荷载工况

根据要求，首先验算以下4种工况。

a）工况一 恒荷载+城市-A级车道荷载，计算现行设计荷载作用下桥梁结构的抗倾覆能力。

b）工况二 恒荷载+1.3×城市-A级车道荷载，该工况用于计算一般超载的情况。

c）工况三 恒荷载+70 t车辆荷载，车队纵向布置为两车前后轴间距4.5 m，结合常见超载车型参数分析统计，并依据《城市桥梁设计规范》（CJJ 11—2011），取单车车重为70 t的车队荷载模拟交通荷载，车辆参数和轴距分布取值同《城市桥梁设计规范》（CJJ 11—2011）。

d）工况四 恒载+1.3倍工况三荷载，模拟可能出现的最不利超载情况。

3 抗倾覆稳定性分析

3.1 有限元分析模型

为了准确分析桥梁结构的空间受力情况，采用空间梁格法[3]对该桥的上部结构进行建模，利用Midas Civil分析软件实现对桥梁上部结构的模拟，全桥模型共划分节点217个，单元268个。根据桥梁竣工图纸提供的桥梁曲线参数确定桥梁结构节点坐标，结构的有限元模型如图1所示，该桥的支座布置形式如图2所示。

图1 结构离散图

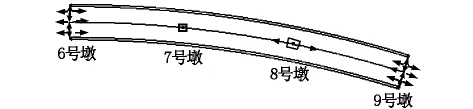
图2 支座布置图

3.2 支反力计算

该联上部结构为钢筋混凝土连续箱梁桥[4]，根据桥梁抗倾覆计算的分析特点，首先计算桥梁结构在成桥状态下的恒载支反力。然后分别对上述各工况汽车荷载进行加载，计算恒载与各工况汽车荷载作用下的支反力，支座反力计算结果见表1。

表1 支座最小反力 kN

3.3 箱梁桥抗倾覆稳定系数计算

3.3.1 上部结构的抗倾覆分析[5]过程

a）根据结构形式和支座布置，确定倾覆轴线。倾覆轴线为单向受压支座依次脱空，最终有效的两支座的连线。

b）按照倾覆轴线，计算抗倾覆力矩和汽车荷载的倾覆力矩。

c）验算上部结构的抗倾覆稳定系数。

该联桥最不利的倾覆轴线为直线A，即7、8号桥墩支座连线，如图3所示。

图3 桥梁结构倾覆轴线

3.3.2 各工况下稳定系数计算

a）工况一 抗倾覆力矩为：

∑RGixi=1 334.4×0.16+674.7×2.98+956.9×5.81+1346.2×0.16+661.9×2.98+960.1×5.81=14242.15kN·m，该桥设计荷载为城市-A级荷载，该桥最大跨径为30 m，所以 qk=10.5 kN/m，Pk=280×1.2=336 kN，倾覆力 矩 为 （1+μ）（qkΩ+Pke）= （1+0.189）×（10.5 ×189.62+336×3.22）=3 657.75 kN·m.

所以，箱梁抗倾覆稳定系数：

b）工况二 保持抗倾覆力矩不变，倾覆力矩为1.3倍工况一，则抗倾覆稳定系数为：

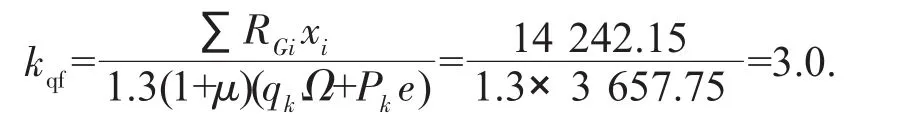
c）工况三 采用特殊车列，手动加载，通过多次试算，选择图4加载布置得出最大加载效应，计算抗倾覆稳定系数。

该工况倾覆力矩为：

所以，箱梁桥抗倾覆稳定系数：

图4 工况三车列布载

d）工况四 保持抗倾覆力矩不变，倾覆力矩为1.3倍工况三，则抗倾覆稳定系数为：

各相应工况下上部结构的抗倾覆稳定系数汇总见表2。

表2 不同工况下抗倾覆稳定系数

4 最大通行能力研究

由上述工况一至工况四计算结果可知，桥梁结构在设计荷载作用下以及最大超载情况下抗倾覆系数在工况一、工况二情况下没有超过系数2.5，但在工况三、工况四情况下，抗倾覆系数小于2.5，所以工况三、工况四不满足规范要求。然而在工况一至工况四荷载作用下，桥梁结构各墩支座均不会发生脱空现象，可见，桥梁支座脱空的临近荷载与桥梁倾覆的临界荷载有很大区别。

为了计算分析桥梁结构正常使用极限状态（支座不脱空）[6]以及承载能力极限状态（抗倾覆稳定系数达临界值2.5）的实际通行最大荷载，调查了该匝道桥的交通荷载，经统计和分析，白天交通量较大，但主要以小汽车为主，夜间交通量虽小，但渣土车为主要交通荷载，车辆吨位大。根据桥梁全长、最不利倾覆轴与偏载车道布置以及车辆轴距分布，结合支座反力影响线，分别定义了3种不同的实际交通车辆（单辆车车重30 t，轴距分布见图5所示）排列成车队过桥情况，即单车过桥、双车过桥、三车过桥，车队行驶车道均为最不利偏载车道，从而确定该联桥在两种状态下最大通行荷载。

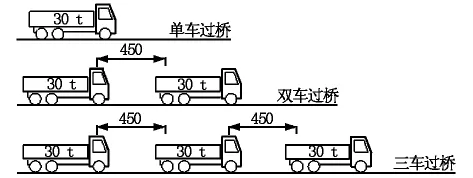
图5 不同车队过桥示意图

工况一单车过桥计算以实际通行车辆加载，车重为30 t，抗倾覆力矩不变，因此抗倾覆稳定系数为：

所以，箱梁抗倾覆稳定系数：

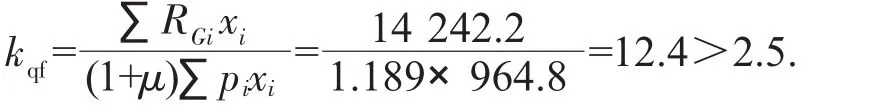
图6 单车过桥车列布载

当抗倾覆稳定系数达到临界值2.5时，对应的车辆重量为：

即单车过桥时，轴距分布与30 t实际通行车辆一致，车重达149.0 t时为临界倾覆情况。

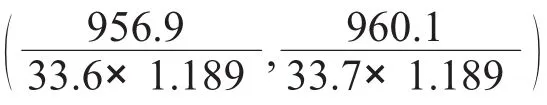
表3 不同工况下最大通行荷载（单车车重：t）

5 结语

本文以某地区匝道桥为工程实例，针对独柱墩连续弯桥的抗倾覆性能进行了验算，依据规范的计算方法，并基于设计荷载定义了4种不同的荷载工况，计算结果表明车道荷载下该匝道桥的抗倾覆稳定系数均满足要求，车辆荷载下抗倾覆安全系数不足；此外，以该匝道桥车辆调查数据为依据选择实际通行较为不利的重载车型进行布载，对该车型以3种不同的工况即单车、双车和三车过桥，桥梁发生倾覆或支座脱空时单车最不利荷载进行计算，结果表明三车同时过桥载重超载20 t时桥梁发生倾覆的可能性较大。