考虑承载力分布特性的基桩可靠度研究
2015-01-14王涝谦
王涝谦
(山西路桥第一工程有限责任公司,山西 太原 030006)
0 引言
近年来,随着我国经济快速发展,桩基础应用十分广泛,包括公路、铁路、港口等重大基础建设[1]。但是,桩基工程作为隐蔽工程,涉及到地质勘测、桩基施工和桩基选型等多个方面。桩基工程的成败决定了工程质量和安全。桩基础是深基础的主要型式之一,它是通过桩侧摩阻力和桩端阻力将上部荷载传递到深部岩土层中[2]。相关的桩基研究成果不断涌现,譬如桩顶的沉降、位移,基桩承载力的计算,桩侧阻力和桩端阻力对桩的总承载力的分担比等。为了研究基桩极限承载力对桩基可靠性的影响,相关研究学者对基桩承载力的实测值和计算值进行无量纲化,将无量纲化后的值定义为基桩承载力的试计比,即基桩承载力的实测值和计算值的比值[3-4],并对试计比进行了较大详细的研究,得出了一些有意义的成果,为桩基规范的修订和完善提供了必要的依据。
目前,研究桩基规范规定的承载力确定方法是否可靠合理的资料很少,本文利用现有的基桩承载力实测和计算资料,基于可靠性原理给出了打入桩和钻孔灌注桩承载力的分布特征,并给出了相应的可靠度计算方法,为桩基设计规范的完善提供了理论依据。
1 基桩可靠度的计算
设计规范规定的基桩承载力确定方法是桩基设计的理论基础。在桩基设计的过程中,其尺寸大小、材料类型、施工方法等因素是建立在规范规定及实践经验的基础上的。但是一般情况下,在桩基施工的过程中,因为受到现场条件、施工技术等因素的影响,桩长、桩径、土质条件等因素会有差异,导致很难得到足够多的可以认为条件相同的单桩承载力的子样本,其承载力的研究也受到很大限制[5]。
为解决这个问题,相关研究者利用单桩承载力试计比研究单桩承载力。单桩承载力的试计比是单桩承载力的实测值(Rm)与理论计算值(Rk)的比值,记为λ,即:

在式(1)中,基桩承载力实测值与计算值的大小存在着以下3种关系。
a)如果基桩的实测承载力大于规范计算的承载力值,即:

则认为该桩是符合实际要求的。
b)如果基桩的实测承载力小于规范计算的承载力值,即:

则认为该桩是不符合实际要求的。
c)如果基桩的实测承载力等于规范计算的承载力值,即:

则认为该桩设计与施工结果达到了一种极限状态。
基于以上论述,对基桩设计的施工效果可建立如式(5)所示的功能函数

其极限状态方程为

由于受到诸多不确定性因素的影响,桩承载力试计比λ应为一随机变量。罗书学[3]通过统计分析、研究发现:钻孔灌注桩承载力试计比用正态分布、对数正态分布或极值Ⅰ型分布来描述是科学合理的;而打入桩承载力试计比可用正态或对数正态分布进行研究。
因此,基桩承载力试计比的分布类型在一定意义来说是具有不确定性的,需要在实践中采用有效的方法进行研究,并利用研究成果分析基桩承载力的可靠性问题。
由可靠性理论知[6],基桩承载力的失效概率的表达式为

可靠度指标的计算公式为

式中,μz表示基桩承载力均值;σz表示荷载均值。
则失效概率和可靠度之间的关系式为

2 实例分析
文献[3]中收集了78根钻孔灌注桩和128根打入桩承载力的相关资料,资料包括了钻孔灌注桩和打入桩极限承载力、极限侧阻、极限端阻及相关试计比的统计结果,为可靠度分析提供了详细的资料。
限于篇幅,详细数据见文献[3],在此不一一列出。
2.1 钻孔灌注桩
对于收集到的78根钻孔灌注桩,其极限承载力试计比λ的散点图及与单位值1相比较得到的频率分布情况分别如图1和图2所示。
由图1可以看出,极限承载力试计比值除个别之外,几乎都分布在0.75~1.45之间;承载力试计比值大都集中在0.9~1.3区间内。因此,将单位1作为一个临界点,试计比λ值散布于其周围。

图1 钻孔灌注桩极限承载力试计比λ散点分布图
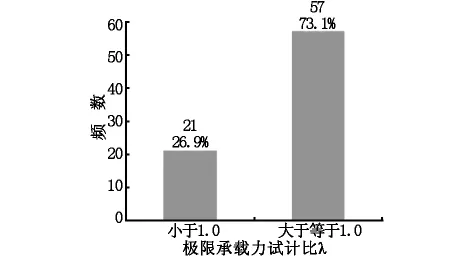
图2 试计比λ频率分布图
由图2可知,极限承载力试计比λ值有73.1%大于或等于1。因此,在一般条件下,单桩的实际承载力不小于计算设计的承载力,体现了其安全可靠性。
除此之外,比较钻孔灌注桩侧阻和端阻对于承载力的分担情况,比较结果如表1所示。实测和计算侧阻分担比都在80%以上,且相差不大,表明钻孔灌注桩的承载力主要有侧摩阻力提供。侧阻差异性衡量值0.005 2很小,表明钻孔灌注桩侧阻的规范计算公式是比较合理的。
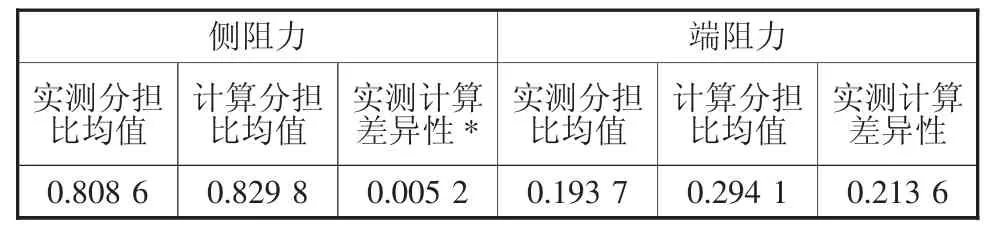
表1 钻孔灌注桩侧阻和端阻对于承载力的分担情况
对于钻孔灌注桩,除了研究其总承载力试计比分布情况以外,依据式(1),分别针对其侧阻和端阻定义了侧阻试计比和端阻试计比,它们的分布特征参数如表2所示。

表2 钻孔灌注桩承载力、侧阻力和端阻力试计比特征参数
由可靠度分析中的中心点法,依据形如式(5)的功能函数,分别计算可得钻孔灌注桩总承载力、侧阻力及端阻力的可靠性水平为:0.235 8,0.117 24,0.411 1。可以看出,对于钻孔灌注桩,端阻力的可靠性水平要比侧阻力高。
2.2 打入桩
由对于收集到的128根打入桩,其极限承载力试计比的散点图、频率分布直方图及与单位值1相比较得到的频率分布情况分别如图3和图4所示。

图3 打入桩极限承载力试计比λ散点分布图
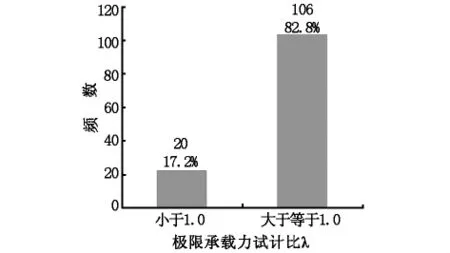
图4 试计比λ频率分布图
由图3可以看出,极限承载力试计比值除个别值以外,几乎都分布在0.8~1.5之间,区间端值较钻孔灌注桩略大;承载力试计比值在0.9~1.5区间内居多,表明单位1作为一个临界点,试计比值散布于其周围,且大多较1偏大。由图4可知,82.8%极限承载力试计比值大于或等于1,较钻孔灌注桩73.1%的比例有较大幅度的提高。表明在一般条件下,单桩的实际承载力不小于计算设计的承载力,体现了其安全性,桩基础处在安全状态,且比钻孔灌注桩基础更可靠。
类似于钻孔灌注桩的分析过程,在此比较了打入桩侧阻和端阻对于承载力的分担情况。其比较结果如表3所示。实测和计算侧阻分担比大都在70%左右,且相差不大,表明打入桩的承载力主要有侧摩阻力提供,但其分担比较钻孔灌注桩有所降低,相反,其端阻得到较大提高;侧阻和端阻差异性衡量值都为0.006 4,很小,表明打入桩侧阻和端阻的规范计算公式是比较符合实际情况的。
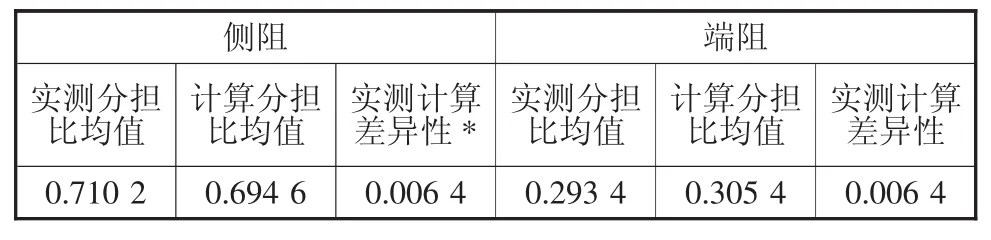
表3 打入桩侧阻和端阻对于承载力的分担情况
对于打入桩,除了研究其总承载力试计比分布情况以外,还依据式(1),分别针对其侧阻和端阻定义了侧阻试计比和端阻试计比,它们的分布特征参数如表4所示。

表4 打入桩承载力、侧阻力和端阻力试计比特征参数
由可靠度分析中的中心点法,依据形如式(5)的功能函数,分别计算可得打入桩总承载力、侧阻力及端阻力的可靠性水平为:0.369 2,0.395 6,0.298 4。可以看出,对于打入桩,侧阻力的可靠性水平要比端阻力高。
3 结论与分析
基于已有资料,研究了钻孔灌注桩和打入桩总承载力、侧阻力及端阻力试计比的分布特征,讨论了侧阻力和端阻力对总承载力的分配情况;并以单桩总承载力、侧阻力及端阻力的试计比为研究对象,将其与单位1作比较,建立了新的桩承载力可靠性分析的功能函数,研究它们的可靠性,得到以下结论:
a)钻孔灌注桩的极限承载力试计比几乎都分布在0.75~1.45之间,在0.9~1.3区间内居多,大部分都大于1;打入桩的极限承载力试计比几乎都分布在0.8~1.5之间,在0.9~1.5区间内居多,大部分都大于1;钻孔灌注桩的极限承载力试计比普遍要比打入桩极限承载力试计比偏小。
b)钻孔灌注桩和打入桩的实测和计算侧阻分担比分别在80%、70%以上,且相差不大,表明钻孔灌注桩和打入桩的承载力主要有侧摩阻力提供,且侧阻的规范计算公式是比较科学合理的。
c)对于钻孔灌注桩,端阻力的可靠性水平要比侧阻力高;对于打入桩,侧阻力的可靠性水平要比端阻力高。
本文的方法为桩基规范的修订和完善提供了一定的理论依据,希望能够引起相关学者和部门的重视,使桩基设计规范更加科学合理。
