基于场协同理论的波纹管强化换热的数值模拟研究*

战洪仁 曹 颖 侯新春 王立鹏 李雅侠

(沈阳化工大学能源与动力工程学院)

换热器是应用非常广泛的换热设备，强化换热器的换热效果一直是国内外学者的研究热点。研究表明，改变换热管结构可明显增强换热效果[1]。波纹管良好的弹性使其具有较强的自除垢特性，因而被国内外学者广泛研究。国内相继有学者对波纹管结构进行研究，结果发现，正弦波纹换热管的综合传热性明显优于其他结构形式的波纹管[2,3]。但关于正弦波纹管局部结构对其传热和流动特性的影响的研究较少。Guo Z Y等从速度场和温度场相互配合的角度分析，提出了对流换热的场协同原理，它能够清晰地显示波纹管内部每一点的换热效果[4,5]，为改变波纹管结构以强化换热提供了理论指导。笔者运用Fluent软件，采用模平均角[6]计算公式来计算场协同角，并以此作为波纹管强化传热场协同性的评价标准，分析不同结构波纹管及其局部的换热机理，研究换热管结构对流动和换热性能的影响。

1 计算模型和数值条件

波纹管管内传热与流动过程受物理守恒定律的支配，即必须遵循质量守恒定律、动量守恒定律和能量守恒定律。计算流体动力学的控制方程是对这些守恒定律的数学描述，控制方程的通用形式为[7]：

笔者选取的正弦波纹管模型如图1所示，当量直径d均取19mm，具体结构参数见表1。

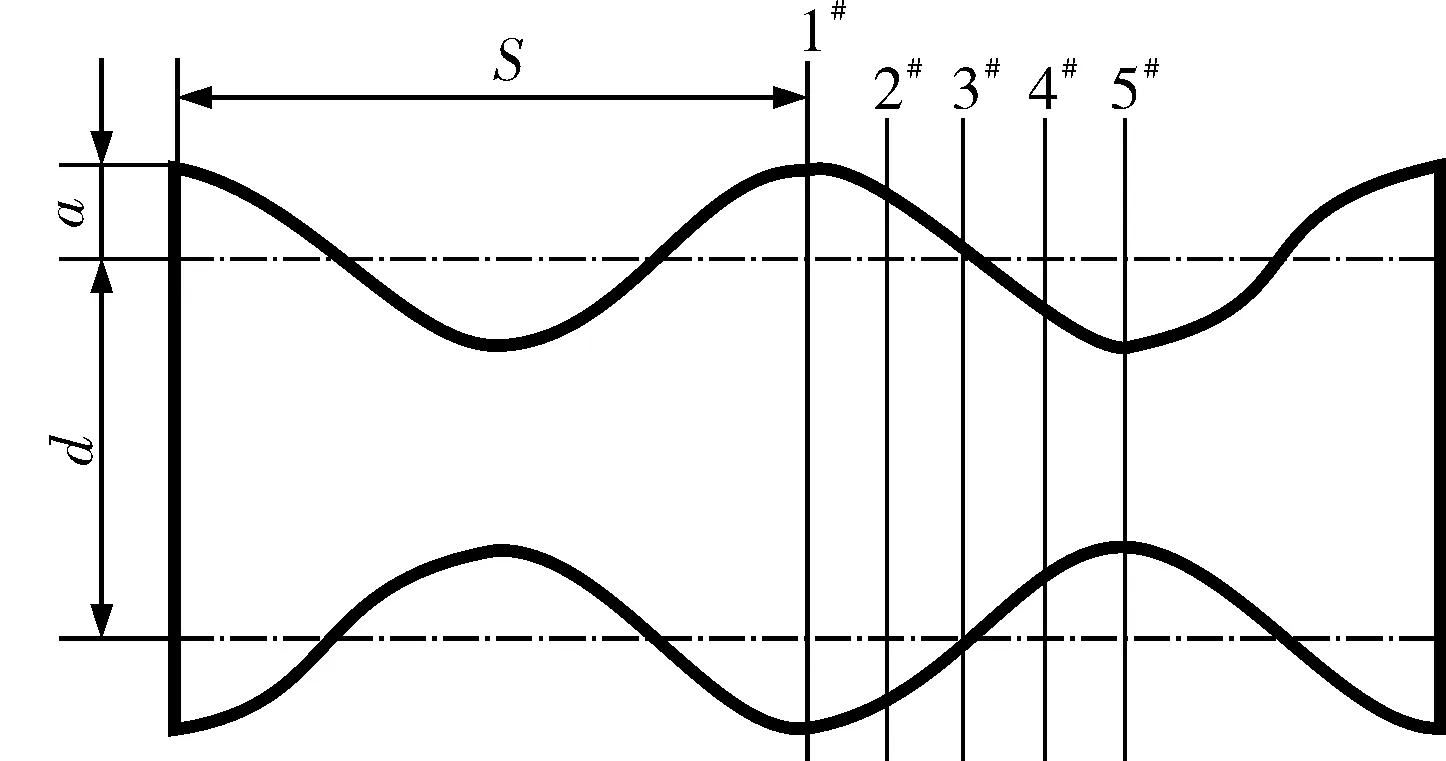
图1 正弦型波纹管模型

mm

流体在波纹管内周期性流动，为了使波纹管充分发展，对管道进行数值模拟计算。选择基于压力的隐式稳态求解器，采用非结构化的六面体网格。能量与动量方程的离散格式采用Quick格式，压力与速度耦合方式采用Simplec算法，收敛条件为连续性方程、动量方程和能量方程的计算残差均小于10-6。以水为工质，入口速度分别取0.3、0.5、0.8、1.0、1.2、1.5m/s。采用质量流量入口(mass- flow- inlet)，压力出口(pressure- outlet)。进口温度300K，管壁温度为恒定值350K。无速度滑移壁面边界条件。不考虑壁面厚度，忽略重力的影响。

2 计算结果与分析

2.1结构参数对波纹管内换热性能的影响

图2为不同换热管(5种结构波纹管和相同当量直径的圆管)的平均Nu数与Re数的关系曲线，从图2可以看出：在研究范围内，Re数相同时，波纹管的Nu数明显高于圆管的；波纹管幅值相同时，其Nu数随着周期的增大而增大；波纹管周期相同时，在低Re数下，幅值的变化对Nu数基本没有影响，当Re≥10000时，随着Re数的增大，Nu数随幅值的增大而增大。综合研究结果可知，在研究范围内，增大波纹管的幅值与周期能够增强波纹管的换热效果，其中波纹管的周期变化对换热效果的影响比较大。

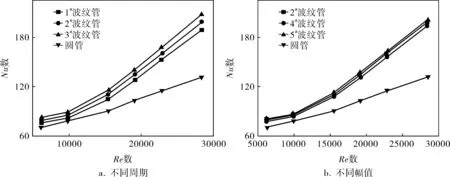
图2 不同换热管的平均Nu数与Re数的关系曲线

2.2结构参数对波纹管内摩擦阻力的影响

通过数值模拟计算出各换热管(5种结构波纹管和相同当量直径的圆管)的摩擦阻力系数f随Re数的变化(图3)。从图3可以看出：波纹管的摩擦摩擦阻力系数比相同当量直径的圆管的磨擦阻力系数高很多；幅值相同时，随着波纹管周期S的增大，摩擦阻力系数逐渐增大；周期相同时，管内摩擦阻力系数随着幅值的增大而增大。但是从图中可以看出，幅值对摩擦阻力系数的影响程度相对较大。

图3 不同换热管摩擦阻力系数f随Re数的变化

2.3传热强化综合因子

传热强化综合因子η是衡量传热性能的一个通用综合性指标，其评价采用Webb提出的方法[8]：

式中f、f0——波纹管和圆管内流体的流体阻力系数;

Nu、Nu0——波纹管和内流体的努塞尔数。

若以提高强化传热的综合性能为目标，则需考虑温度梯度▽u之间的协同性，协同角越大，传热强化综合因子η越高。

图4为波纹管的传热强化综合因子随Re数的变化情况。从图4可以看出：换热管传热强化综合因子均随Re数的增加先减小后逐渐增大，周期与幅值的比S/a为8.17的3#管的传热综合性能最好，S/a为7.17的1#管的传热综合性能最差，这一结论为工程应用选择管型提供了依据。

图4 换热管的传热强化综合因子η随Re数的变化

2.4场协同理论分析换热机理

图5为平均场协同角随Re数的变化情况，从图5可以看出，波纹管的协同角明显小于圆管的协同角，且3#管的平均协同角比1#管的平均协同角小很多，这说明波纹管的换热性能优于圆管的换热性能，3#管的换热效果优于1#管的换热效果。

图5 平均场协同角随Re数的变化

图6为3种结构的换热管径向截面上的场协同云图，从图6可见，波纹管壁面处的协同角比圆管的小，且3#管壁面处的协同角最小，因此3#管的结构对传热效果的影响是显著的。图7为波纹管在同一流速下的温度等值线和速度矢量分布，由图7可以看出，波纹结构使流体在波峰处出现了回流涡，流速分布发生了明显的改变，温度梯度的方向与流速矢量方向的夹角明显变小，场协同性变好，这说明湍流增强，边界层变薄，波峰处的换热效果明显。

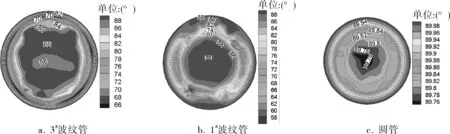
图6 3种换热管径向截面上的场协同云图

图7 波纹管在同一流速下的温度等值线和速度矢量分布

图8为波纹管内流速为1.2m/s时不同截面的流线图。从图8a可以看出：波纹管内波峰靠近壁面处，并在二次流的作用下形成旋涡，很大程度上强化了壁面的换热特性；而波谷中间位置的流线趋于平稳，换热性能较差。从图8b、c可以看出：虽然在波谷中心处形成小旋涡，但在壁面处流线趋于平稳，换热性能较差。综上可知，要提高波纹管的换热性能，应从改善波谷的换热特性着手。

3 结论

3.1波纹管周期变化对Nu数的影响较大，Nu数随着周期的增大而增大；管内摩擦阻力系数主要受幅值的影响，随着幅值的增大而增大。

3.2换热管传热强化综合因子均随Re数的增加先减小后逐渐增大，周期与幅值的比S/a为8.17的3#波纹管传热综合性能最好，S/a为7.17的1#管传热综合性能最差。

3.3从场协同角度分析了波纹管局部的换热效果，发现波纹管波峰处的换热效果很好，波谷处的换热效果较差，因此强化波纹管换热性能可从改善波谷的换热性能着手。

[1] 方书起，祝春进，吴勇，等. 强化传热技术与新型高效换热器研究进展[J]. 化工机械，2004，31(4)：249～253.

[2] Mahmud S, Sadrul Islam M,Feroz C. Flow and Heat Transfer Characteristics Inside a Wavy Tube[J].Heat and Mass Transfer, 2003, 39(5/6):387～393.

[3] 曾敏，王秋旺，屈治国，等. 波纹管内强制对流换热与阻力特性的实验研究[J]. 西安交通大学学报，2002，36(3)：237～240.

[4] Guo Z Y, Li D Y, Wang B X. A Novel Concept for Convective Heat Transfer Enhancement[J]. International Journal of Heat and Mass Transfer, 1998, 41(14):2221～2225.

[5] 李志信，过增元.对流传热优化的场协同理论[M]. 北京：科学出版社，2010：55～68.

[6] 周俊杰，陶文铨，王定标.场协同原理评价指标的定性分析和定量探讨[J].郑州大学学报(工学版)，2006，27(2)：45～47.

[7] 陶文铨.数值传热学[M]. 西安：西安交通大学出版社，2001：1～26.

[8] Webb R L, Eckert E R G. Application of Rough Surfaces to Heat Exchanger Design[J].International Journal of Heat Transfer ,1972,15(9):1647～1658.