一种多智能体自适应蜂拥控制算法

秦补枝

(南京化工职业技术学院自动控制系，南京 210048)

近年来，蜂拥控制逐渐成为人们研究的热点问题之一[1～5]。它主要是研究具有有限感知能力的多个个体涌现出来的全局行为，比如鱼群与鸟群的群体行为。蜂拥控制问题的研究也在工程中有重要应用，如无线传感网络、无人驾驶飞机编队及水下机器人地形探测等[5,6]。在文献[7，8]中提出了蜂拥控制问题的3条Reynolds基本规则：分离，与邻域内的智能体避免碰撞；聚合，与邻域内的智能体保持紧凑；速度匹配，与邻域内的智能体速度保持一致。此后，许多控制学者通过构造人工势函数并结合速度一致算法实现Reynolds的3条规则[9～14]。在文献[8]中Olfati S R提出的算法结合了简单的人工势函数，在对多智能体系统控制过程中实现了Reynolds模型的3条基本规则。

在以上这些研究中，大部分都假设智能体的速度大小保持一致，这在实际工程中很难实现。因为智能体的感知范围有限，保持速度大小不变很容易产生分裂现象，脱离群体运动。所以，笔者提出一种自适应速度策略以提高蜂拥行为，使智能体在运行途中不仅能自适应改变速度方向，而且能自适应改变速度大小。

考虑N个智能体在n维欧式空间中运行，其中第i个智能体的运动方程为：

②数据处理与分析。在此次调查中，经常使用统计软件从事相关工作占样本的63%，利用统计数据进行相关知识的教学占比76.6%。从这两方面来看，内蒙古高校教师在实践教学中数据处理能力有待加强。

(1)

其中，qi∈Rn，代表智能体的位置向量；pi∈Rn，代表智能体的速度向量；ui∈Rn，代表智能体的控制输入(加速度)向量。

有限区间上光滑的人工势函数为[7，8]：

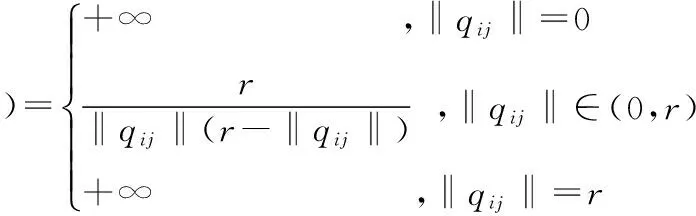
(2)

其中，‖qij‖=‖qi-qj‖，表示两个智能体之间的距离。

b. 系统达到蜂拥时总能量达到最小。

将双创教育与专业教育有机融合，全过程渗透，培养学生的创造性思维，提升学生的开拓进取能力和锲而不舍的态度，避免双创教育和专业教育的相对独立及脱节问题，这才是双创教育的根本目的。

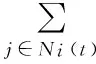
(3)

It was shown that hyperphosphatemia is an independent factor determining the unfavorable prognosis,accelerating the progression of IHD,aggravating systolic hypertension and LVH,increasing the risk of arrhythmia,as well as acute and congestive HF in patients on LTH[56].

(4)

国家发展改革委、水利部第4号令颁布的《水利工程供水价格管理办法》第四条规定，“水利工程供水价格由供水生产成本、费用、利润和税金构成”，“供水生产成本是指正常供水生产过程中发生的直接工资、直接材料费、其他直接支出以及固定资产折旧费、修理费、水资源费等制造费用。供水生产费用是指为组织和管理供水生产经营而发生的合理销售费用、管理费用和财务费用”。

定理 考虑一个具有N个智能体的系统，它们的运动方程为式(1)，每个智能体的控制输入为式(3)。假设初始的能量为一个有限值，可以得到如下结论：

a. 所有智能体的速度都会趋向一致；

笔者提出自适应速度蜂拥控制算法：

高校官网是以高校为主题，面向全社会，以教师、学生和管理人员为主要服务对象，以网络教学、信息沟通、教学管理和对外宣传为基本使命的工作平台，是高校信息化建设的基础和必经阶段。[1]高校网站体现的是高校主体的意志，其主要服务对象是教师、学生及管理人员，同时高校网站也是面向全社会的窗口，在全球化国际化的大环境下，各大高校希望能与国际接轨，高校网站正是向国际社会展示自身的最简便也最重要平台。

证明 定义系统的总能量函数为：

对于两个智能体之间相互影响时wij=wji>0，否则wij=wji=0。

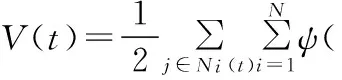
从式(5)可以看出，V(t)的各个要素都是半正定函数，所以V(t)也是半正定函数。

(5)

式中vij——常数；

ε——所有边的集合。

根据四川某军工单位的某型飞机特殊零件的测试需求，研制了一套机电液一体化的测控系统。该测控系统中，根据试验要求，存在多种需要采集的信号，包括模拟信号、数字信号、脉冲信号等，根据其采集信号的不同采用不同采集标准的采集卡获取数据是设计该系统的关键所在。本文根据相应的技术协议书的要求，对数据采集系统的软件模块进行了分析，然后采用适配器模式、装饰者模式和单例模式对其进行具体实现，通过这3种设计模式的实际应用效果表明数据采集系统软件模块除拥有较高的可拓展性外，其可靠性、灵活性与复用性也得到了极大的提高。

总能量函数V(t)对时间的导数为：

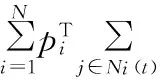
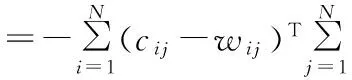
(6)

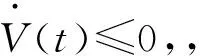
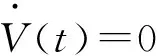
(7)

所以，系统达到蜂拥时总能量达到最小。

2 仿真结果

仿真采用5个智能体在平面上运动，初始网络必须保持连通。它们的初始位置和初始速度随机产生于[0,10]×[0,10]和[0,0.1]×[0,0.1]的范围内，邻域半径为3；自适应增益β=0.2。图1是5个智能体的运动情况。实心圆点代表智能体，两点之间有连线表示智能体之间的邻域关系，箭头方向表示智能体的速度方向，箭头长短表示智能体的速度大小。

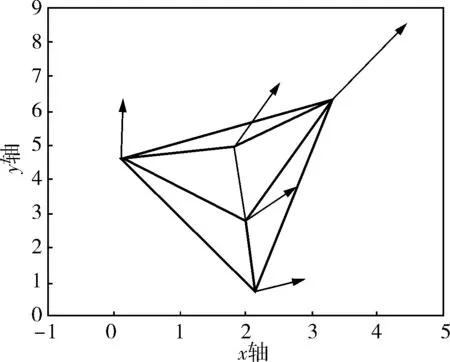
a. t=0s

b.t=8s

c. t=20s

可以看出，系统中的智能体在控制器控制过程中逐步靠近，并不断地对自身的状态进行调整，经过约20s的调整后，整个智能体系统达到稳态，拓扑结构不再发生变化。因此，多智能体自适应蜂拥控制的控制器是可行的，达到了蜂拥控制的效果。

在电子对抗阶段，因为借助于软件环境，准备阶段的工作量不是很大。在实施过程中，由5人组队，组建在同一市场环境下竞争的企业，分别担任公司的总经理、人力资源总监、财务总监、销售总监、研发总监；比赛正式开始前两天进行两期的指引培训，使参赛选手熟悉流程；之后进入正式比赛，根据主持人的指示依次完成每一步的决策；每月为一期，进行2-4轮后最终确定比赛结果。

根据《施工图审查制度的思考》，在住建部系统中，2013年之前，已经开始使用施工图审查信息网站、短信平台、内部OA系统等方式，加强信息管理。

3 结束语

笔者提出了一种多智能体自适应速度策略，该策略能够调整智能体速度的大小和方向。仿真结果表明，笔者设计的蜂拥控制算法是可行的，实现了多智能体蜂拥行为，即系统中的所有智能体在控制器的作用下逐步靠近，经过一定时间的调整，系统能进入稳定状态。

[1] Mei J,Ren W,Ma G F.Distributed Coordination for Second-order Multi-agents Systems with Nonlinear Dynamics Using only Relative Position Measurements[J].Automatica,2013,49(5):1419～1427.

[2] Cucher F, Dong J G.A General Collision-avoiding Flocking Framework[J].IEEE Transactions on Automatic Control,2011,56(5):1124～1129.

[3] Galbusera L, Ferrari T G, Scattolini R.A Hybrid Model Predicative Control Scheme for Containment and Distributed Sensing in Multi-agent Systems[J].Systems & Control Letters,2013,62(5):413～419.

[4] Guo W L,Lü J H,Chen S H,et al.Second-order Tracking Control for Leader-follower Multi-agent Flocking in Directed Graphs with Switching Topology[J].Systems & Control Letters,2011,60(12):1051～1058.

[5] Gupta R,Bandyopadhyay B,Kulkarni A M.Power System Stabilizer for Multi-machine Power Systems Using Robust Decentralized Periodic Output Feedback[J].IEE Proceedings of Control Theory and Applications, 2005,152(1):3～8.

[6] Haddad W M,Chellaboina V.Nonlinear Dynamical Systems and Control:a Lyapunov-Based Approach[M].New Jersey：Princeton University Press,2008.

[7] Reynolds C W.Flocks,Herds,and Schools:a Distributed Behavioral Model [J].Computer Graphics,1987,21(4):25～34.

[8] Olfati S R.Flocking for Multi-agent Dynamic Systems: Algorithms and Theory[J].IEEE Transactions on Automatic Control,2006,51(3):401～420.

[9] Su H S,Wang X F,Chen G R.A Connectivity-preserving Flocking Algorithm for Multi-agent Systems Based Only on Position Measurements[J].International Journal of Control,2009,82(7):1334～1343.

[10] Olfati S R,Jalalkamali P.Coupled Distributed Estimation and Control for Mobile Sensor Networks[J].IEEE Transactions on Automatic Control,2012,57(10):2609～2614.

[11] Su H S,Zhang N Z,Chen Z Q,et al.Adaptive Flocking with a Virtual Leader of Multiple Agents Governed by Locally Lipschitz Nonlinearity[J].Nonlinear Analysis:Real World Applications,2013,14(1):798～806.

[12] Wang H L.Flocking of Networked Uncertain Euler-Lagrange Systems on Directed Graphs[J]. Automatica,2013,49(9):2774～2779.

[13] Zhang Y J,Li X.Flocking of Multi-agent Systems via Model Predicative Control Based on Position-only Measurements[J].IEEE Transactions on Industrial Informatics,2013,9(1):1377～1385.

[14] 陈世明,李慧敏,谢竟,等.基于局部估计的功率驱动多智能体网络牵制蜂拥控制算法[J].控制与决策,2013,28(8):1190～1194.