蚁群优化的改进型神经网络控制器设计

2015-01-13温阳东

化工自动化及仪表 2015年7期

朱闯林勇温阳东

(合肥工业大学电气与自动化工程学院，合肥 230009)

由于实际生产过程中对象的时变性、非线性、耦合性和不确定性，常规PID控制系统控制效果不理想[1]。神经网络控制具有较强的函数逼近能力，既具有传统PID控制器的优良特性，又具有自学习及并行分布处理等特点，适用于对复杂非线性系统进行建模和控制[2，3]。但是神经网络有自身的缺陷，比如BP神经网络对参数初始值的敏感性、易陷入局部极值及采用固定激活函数时的泛化能力不足等问题[4，5]。随着诸如遗传算法、粒子群算法及蚁群算法等智能群算法逐渐成为研究热点，也为神经网络的优化提供了新思路[6，7]。蚁群算法采用正反馈搜索机制、分布式计算和启发式策略能对神经网络进行优化，但是传统蚁群算法的处理能力有限，容易出现收敛速度慢及容易陷入局部最优解等问题[8，9]。

笔者用可调节激活函数提高网络的泛化能力，改善神经网络性能，并对蚁群算法加以改进，加快算法收敛速度、避免局部最优解。利用改进型蚁群算法优化神经网络的参数，避免其陷入局部极值。仿真结果表明优化后的改进型神经网络控制器对于非线性时变系统起到了良好的控制效果。

控制结构框图如图1所示，首先利用改进蚁群算法优化神经网络的权值和激活函数的参数初始值，改进型神经网络在线调整连接权值和激活函数，并输出增量式PID控制器的3个参数。

图1 系统结构框图

2 神经网络参数推导

(1)

同理可得隐含层的连接权值的调整公式为：

(2)

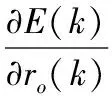
(3)

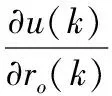
(4)

隐含层激活函数参数调整为：

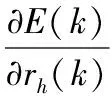
(5)

(6)

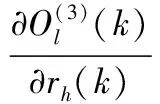
(7)

3 改进蚁群算法优化神经网络参数

蚁群算法(ACO)是模拟自然界蚂蚁觅食过程中在路径上留下信息素并以此指导同伴进行路径选择的仿生算法，是正反馈原理和启发式相结合的产物。在早期过程中，各路径上信息素差别不大，蚁群主要是根据距离的启发式信息来寻找最优解；当算法迭代到一定次数后，较优路径上的信息素明显高于其他路径，这时蚁群主要是通过信息素的交互来寻优。由此可见基本ACO算法早期发现的最优解会使蚁群走向局部最优解，算法出现停滞现象。解决停滞现象的方法就是既要使得算法的搜索空间尽可能大，以寻找可能存在最优解的解空间；同时也要充分利用有效的历史信息，使得算法搜索的侧重点放在已经搜索到的可能是最优解的空间上，从而以更大的概率收敛到全局最优解。

[7]主要从以下3个方面对ACO算法加以改进：将信息素限制在一定范围内，避免某些路径上信息素过低，如最大-最小蚂蚁系统(MMAS)；加强对历史信息的学习，如最优解保留系统蚂蚁系统(ASelite)；根据算法的状态，通过动态调节挥发系数等参数来避免停止现象，如自适应蚁群算法(AACA)。为了避免蚁群算法陷入局部最优解，加大对节点的探索能力和加快算法收敛速度，笔者主要从局部信息素和全局信息素更新方式上对算法进行改进。

局部信息素更新公式为：

τij(k+1)=(1-λ)τij(k)+λu(k)

(8)

其中λ∈(0,1)为可调参数，τij为第i个参数取值集合Ixi的第j个节点的信息素；在搜索的起始阶段应当缩小局部最优解和最差解之间信息素的差别，扩大算法的搜索范围；在中间阶段，u(k)应当增大，以保证搜索速度；在最后阶段，最优解基本确定，u(k)应继续增大，使算法迅速收敛。

(9)

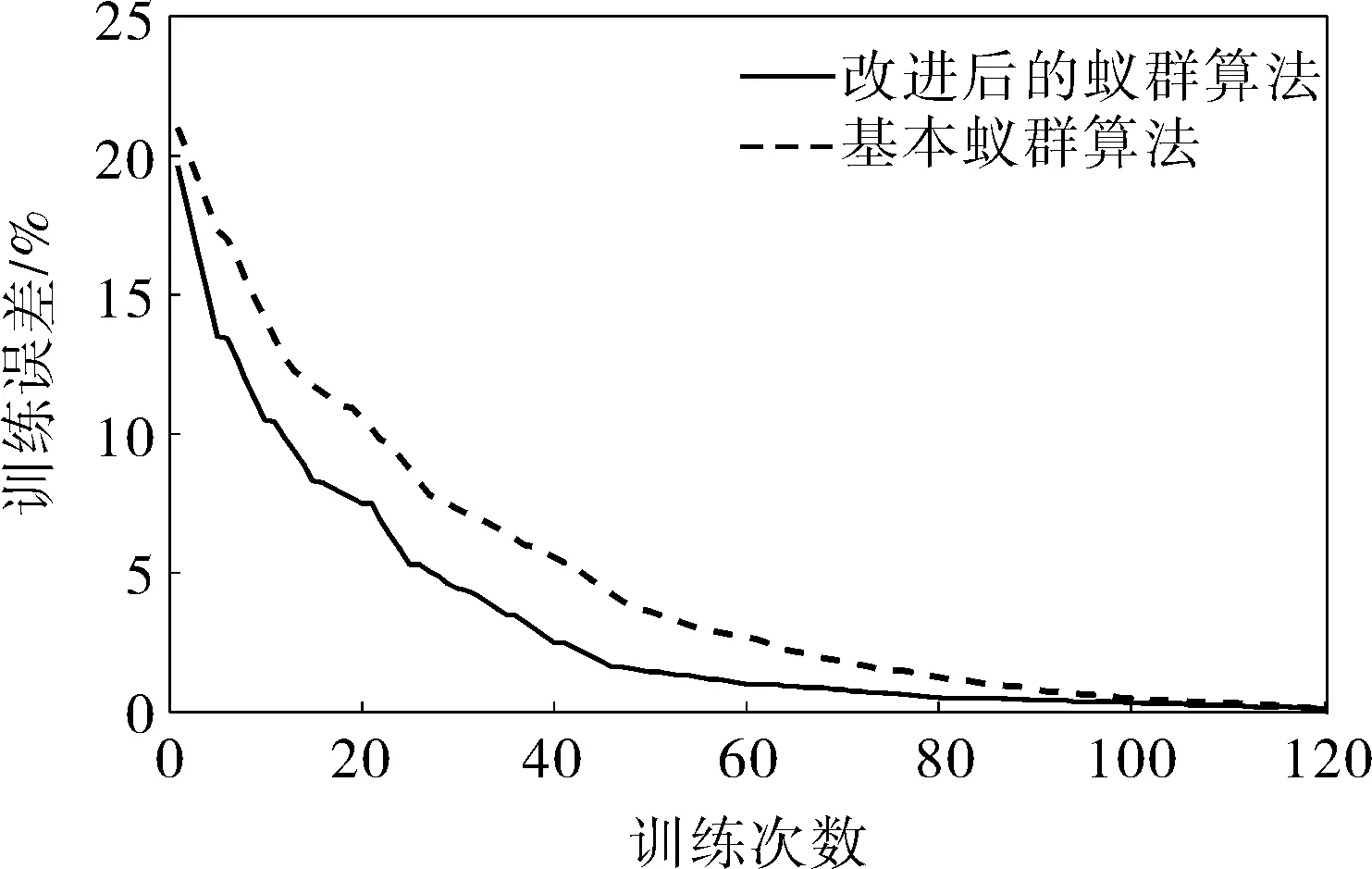
其中k为循环次数，y1

基本蚁群算法中只对最优节点组合进行信息素加强，减小了选择的随机性，容易陷入局部最优，为此，对全局信息素更新方式加以修改，并对信息素挥发系数进行自适应调整。全局信息素更新公式为：

τij(k+1)=w(1-ρ)τij(k)+Δτij(k)

(10)

其中Δτij(k)=Q/f(k)表示本次循环中蚂蚁在第j个元素上的信息增量，ρ为信息素的挥发系数，Q为一正常数，f(k)为目标函数值，文中选为训练误差平方。设minf(k)为到第k次循环为止f(k)的最小值。若f(k)≤minf(k)，说明本次选择的节点比之前的最优解好，应减小信息素挥发，取w=k1(k1>1)；反之若f(k)>minf(k)，取w=k2(k2<1)。

用蚁群算法优化神经网络参数属于连续优化问题，具体步骤如下：

a. 估计神经网络m个参数xi(1≤i≤m)的取值范围[xil，xiu]；

b. 将各变量范围N等分，hi=(xiu-xil)/N，形成集合Ixi；

c. 若到hi<ε，则算法停止，所选节点值为最优解xi*=(xil+xiu)/2；