认知无线电带宽频谱感知性能分析及优化

刘 鑫， 仲伟志

(南京航空航天大学航天学院，江苏 南京210016)

认知无线电(cognitive radio，CR)通过允许次用户(secondary user，SU)择机使用主用户(primary user，PU)未使用的空闲信道，大幅度提高现有频谱资源的利用率［1］.SU 在进行数据传输时，需要通过频谱感知检测信道中是否存在PU，如果检测到PU 存在，SU 必须停止传输，避免对PU产生干扰［2-4］.由于SU 无法预知PU 信号的先验信息，因此通常采用能量检测感知PU［5］.

目前，CR 大都采用时间频谱感知模型，即SU在每个帧的起始阶段感知PU，检测到PU 空闲后，用剩下的帧时间传输数据.例如，Marinho 等提出了“先听后传”的CR 媒体访问控制(media access control，MAC)层协议，通过在MAC 层传输前先检测，可以降低SU 对PU 的干扰［6］;丁汉清等采用能量检测感知PU，用SU 平均信道效率衡量CR 系统性能，分析了在SU 频谱感知的不同阶段，感知时长对CR 系统性能的影响［7］;Liang 等提出了感知吞吐量折中模型［8-9］，通过优化感知时间，最大化SU 的吞吐量;Choi 等指出时间频谱感知不能够准确检测PU，主要因为SU 传输数据时不能够进行频谱感知［10］.

本文提出了带宽频谱感知模型，SU 在每个帧使用部分带宽进行频谱感知，其余带宽传输数据.因此，SU 可以在整个帧周期内实时监测PU 的状态，避免对PU 产生干扰.

1 能量检测和PU 状态模型

1.1 能量检测

SU 最常用的频谱感知方法是能量检测，能量检测执行迅速且不需要PU 信号的先验信息.能量检测通过将SU 接收到的信号能量与预先设定的门限作比较，实现对PU 存在与否的判断. 如果能量值小于门限，表明信道中只有噪声，不存在PU信号，否则SU 将判断信道中存在PU.SU 接收到的信号y 可以采用二元假设，表示为［11］

式中:n 是方差为σ2的高斯白噪声;s 是功率为ps的PU 信号;h 是SU 和PU 间的信道增益;假设Ω0和Ω1分别表示PU 不存在和存在两种状态;m=1，2，…，M，M 是信号样本数.

如果信号带宽为W、检测时间为t，则

接收信号的能量统计值为

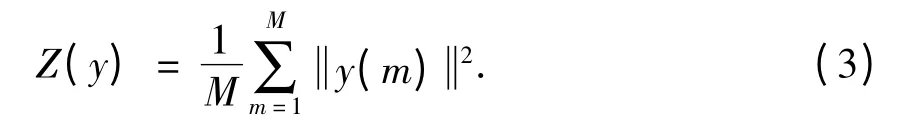
当M 比较大时，根据中心极限定理，Z(y)近似服从高斯分布，表示为

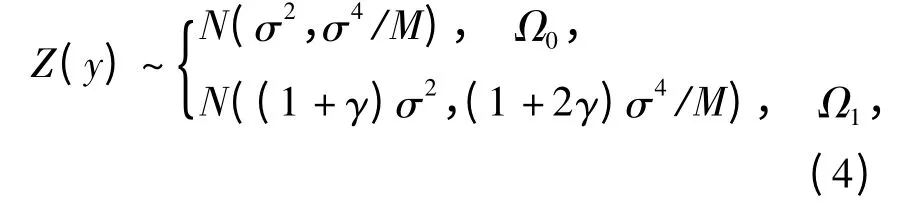
式中:N(x，y)表示均值为x、方差为y 的高斯分布;信噪比γ=psh2/σ2.

根据式(4)，能量检测的虚警概率Pf和检测概率Pd分别表示为［12］

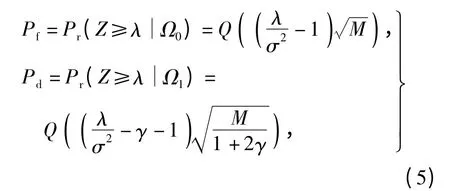
根据式(2)和(5)，Pf由Pd表示为

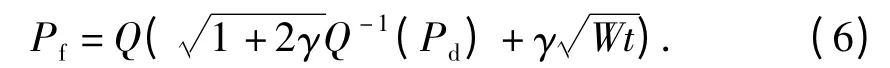
1.2 PU 状态模型

PU 的状态变化可以建模为ON-OFF 马尔科夫随机过程［13-14］. ON 表示PU 存在，即假设Ω1;OFF表示PU 不存在，即假设Ω0.如图1 所示，PU 的不存在和存在概率分别表示为

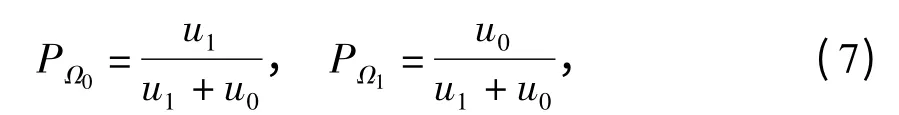
式中:u0和u1分别表示Ω0到Ω1和Ω1到Ω0的状态转移速率.帧周期T 内，PU 不存在的持续时间表示为

图1 PU 状态模型Fig.1 PU state model

2 带宽频谱感知性能分析

2.1 感知模型和干扰

SU 在每个帧的开始使用多信道频谱感知技术从多个可用的信道中选择一个最可能空闲的信道［15］.多信道频谱感知是初始感知，主要使SU 能够快速切换到新的信道，因此感知时间短、检测性能粗糙. 当SU 将工作频率调整到某一信道，需要再次对该信道上的PU 进行频谱共享感知，并最终确定是否可以占用这个信道.

传统的时间频谱感知中［6-9］，SU 采用单根天线使用部分时间进行频谱共享感知. 如图2 所示，只有当检测到PU 不存在时，SU 才能够进行数据传输，否则SU 必须停止传输或转移到其它空闲信道传输.时间频谱感知模型的缺陷是，当SU 传输数据时不能够进行频谱感知，此时如果PU 出现，SU会对PU 造成严重干扰.

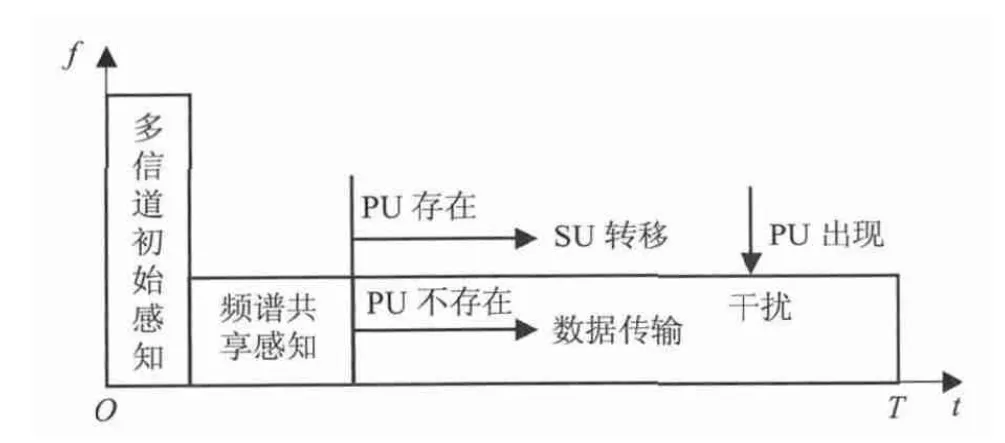
图2 时间频谱感知模型Fig.2 Time spectrum sensing model

本文提出带宽频谱感知模型，SU 采用两根天线，一根天线用于实时频谱感知，另一根天线用于传输数据.每个帧内，SU 使用部分带宽进行频谱共享感知，其余带宽用来传输数据. 如图3 所示，SU的频谱共享感知和数据传输是同时进行的，因此SU 在整个数据帧内可以随时检测PU 的活动状态.SU 一旦发现PU 存在，需要利用感知天线重新进行多信道初始感知.如果发现空闲信道，SU 可以转移到该空闲信道继续通信，否则SU 必须停止数据传输避免对PU 产生干扰.

图3 带宽频谱感知模型Fig.3 Bandwidth spectrum sensing model

假设初始感知时间远小于帧周期，且可以忽略不计，时间频谱感知中SU 对PU 的干扰包括:SU漏检PU 产生的干扰和SU 正确检测PU 但PU 再次出现产生的干扰.干扰概率表示为

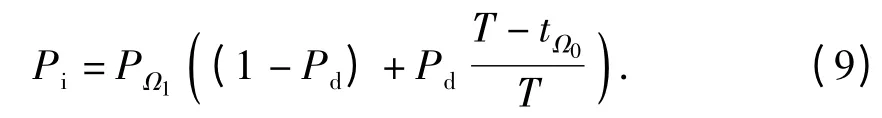
带宽频谱感知中，SU 可以在整个数据帧内实时检测PU 的状态，因此SU 对PU 的干扰仅为SU漏检PU 产生的干扰.干扰概率表示为

2.2 SU 频谱效率

假设频谱感知所占的带宽为αW(0≤α≤1)、SU 的传输带宽为(1 -α)W、SU 正确检测PU 不存在时传输速率为r0、SU 漏检PU 时传输速率为r1，则r0和r1分别表示为［8］

式中:p 是SU 的发射功率.

SU 的频谱效率表示为

将式(6)代入式(12)，有

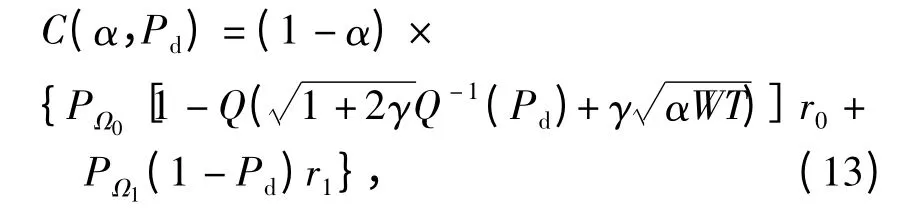
式中:C 是关于α 和Pd的函数.

3 带宽频谱感知优化

带宽频谱感知的优化目标是:在限制PU 受到的干扰和SU 虚警概率的基础上，通过优化感知带宽比α 和检测概率Pd，最大化SU 的频谱效率，表示为

式中:β 是干扰概率上限;Pf≤0.5 是为了保证SU有足够的频谱利用率.

根据式(10)，由Pi≤β 得到Pd≥v(v =1 -β/PΩ1).根据式(13)，由Q(x)的单调递减性得到C(α，Pd)是关于Pd的单调递减函数，即C(α，Pd)≤C(α，v). 因此只有当Pd= v 时，C 才能取得最大值.代入Pd=v，式(14)简化为关于α 的优化问题，表示为

A2=PΩ0r0; A3=PΩ1(1 -v)r1.

首先证明式(15)是凸优化问题，即存在α*∈［0，1］，使得C(α*)取得最大值.

分别求C(α)关于α 的一阶和二阶导数，表示为

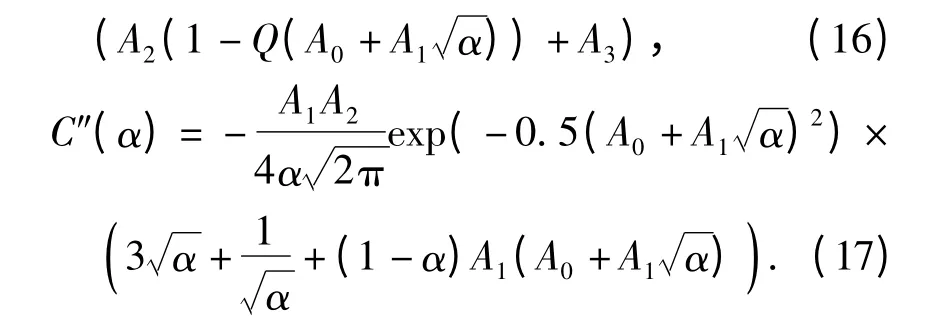
根据式(16)，由A1＞0、A2＞0、A3＞0 和0 ≤Q(x)≤1 得到

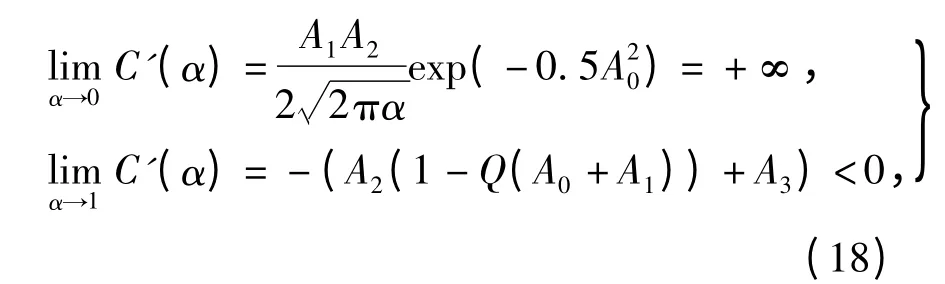
式(18)表明，存在某一α*∈［0，1］，使得C'(α)=0，即α*是C(α)的极值点.

下面说明α*是极大值点. 由Pf= Q(A0+，得到，代入式(17)可知，C″(α)＜0，即C(α)是上凸函数，因此α*是极大值点.

本文采用二分搜索算法［16］寻找C(α)的极大值点α*，算法描述如下:

(1)初始化αmin=0 和αmax=1，以及估计精度δ=10-3;

(2)令α=(αmin+αmax)/2;

(3)如果C'(α)≡C'(αmin)，令αmin=α;

(4)如果C'(α)≡C'(αmax)，令αmax=α;

(5)重复步骤(2)～(4)，直到

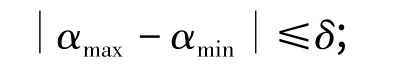
(6)令α*=(αmin+αmax)/2.

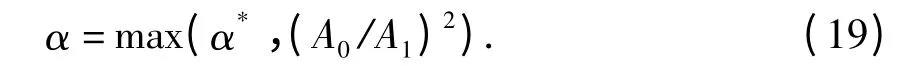
二分算法的复杂度为O(log n)，其中n=1/δ.

4 仿真分析

仿真中，帧周期T=5 ms、带宽W=1 kHz、状态转移速率u0=u1=0.5、噪声方差σ2=0 dB·mW、SU 发射功率p =10 dB·mW，SU 和PU 间信道增益h 服从均值为-10 dB 的瑞利分布，PU 信号的调制方式为QAM (quadrature amplitude modulation).

图4 是本文的带宽频谱感知模型与文献［8-9］的时间频谱感知模型中SU 干扰概率的比较. 从图4 中可以看出，在相同Pf下，带宽频谱感知可以有效地降低对PU 的干扰，这是因为带宽频谱感知在SU 的传输过程中同步检测PU，避免因为PU 突然出现而产生干扰;SU 的频谱利用率随着Pf增加而降低，因此对PU 的干扰减小.

图4 不同感知模型的干扰概率Fig.4 Interference probabilities of different sensing models

图5 是干扰概率Pf=0.20，0.15，0.10，0.05时，对SU 频谱效率C 的比较.从图5 中可以看出，C 是关于α 的凸曲线，即存在最优的α 使得SU 频谱效率最大.当α 较小和较大时C 都比较小，这是因为α 较小，低频谱感知性能导致SU 频谱利用率较低，而α 较大，高感知带宽导致SU 传输带宽较低.图中C 随着Pi降低而减小，表明提高SU 频谱效率和降低对PU 的干扰是相互排斥的，因此需要合理地选择Pi，使之在频谱效率和干扰间获得折中.

图5 不同干扰概率的SU 频谱效率比较Fig.5 SU spectrum efficiency comparison with different interference probabilities

图6 是SNR 为-4、-6、-8 和-10 dB 时，SU频谱效率C 的比较. 从图6 中可以看出，C 仍然是关于α 的上凸曲线，并且随着SNR 降低而减小.

图7 是Pi=0.02，0.10，0.20 时，带宽感知和时间感知模型频谱效率的比较. 从图7 中可以看出，当Pi=0.10，0.20 时，带宽感知能够获得更高的频谱效率，这是因为当Pi较大时，相同Pi下带宽感知的虚警概率更低，即SU 的频谱利用率更高;当Pi=0.02 时，带宽感知的频谱效率反而略低于时间感知，是因为Pi较小时，两种模型SU 的频谱利用率都很低，而带宽感知由于占用部分带宽进行频谱感知，可用的传输带宽较小.

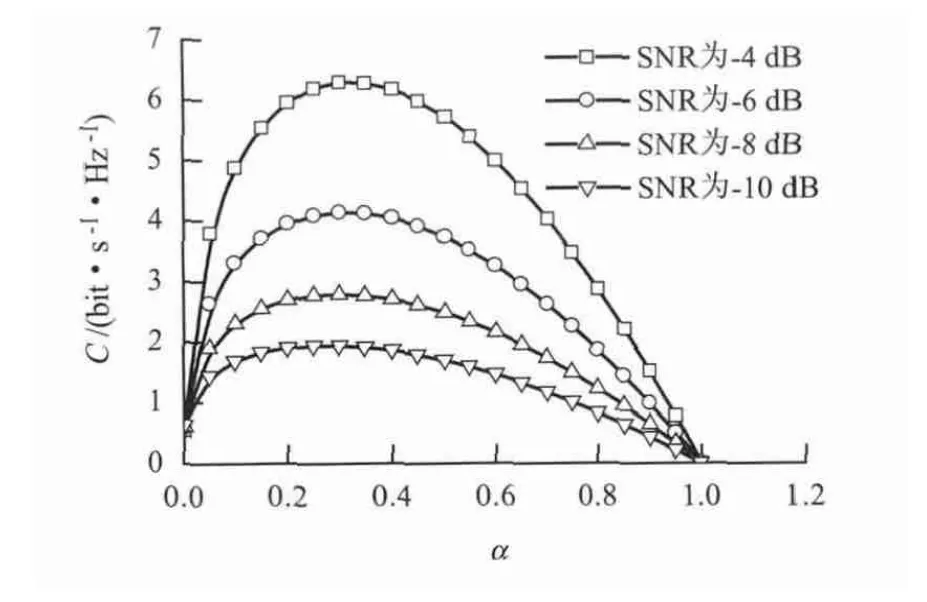
图6 不同SNR 的SU 频谱效率比较Fig.6 SU spectrum efficiency comparison with different SNRs

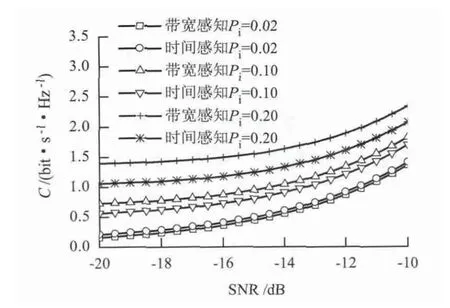
图7 不同感知模型和干扰概率的SU 频谱效率比较Fig.7 SU spectrum efficiency comparison with different sensing models and interference probabilities

图8 比较了不同状态转移速率下，带宽频谱感知中SU 频谱效率. 当u0=0.2，0.5，0.6，0.8 和u1=0.8，0.5，0.4，0.2 时，根据式(7)，相应的PU不存在概率PΩ0=0.8，0.5，0.4，0.2.

图8 不同状态转移速率的SU 频谱效率比较Fig.8 SU spectrum efficiency comparison with different state transfer rates

图8 中显示，当u0=0.2 和u1=0.8 时，SU 的频谱效率最大，此时PU 不存在概率也最大，因此SU 会有更多的机会接入信道.

5 结 论

本文提出了CR 带宽频谱感知模型，允许SU在每个帧内使用部分带宽进行频谱感知，其余带宽传输数据.通过优化感知带宽比和检测概率，SU 能够获得最大的频谱效率. 结果表明，相比时间频谱感知，带宽频谱感知通过实时检测PU 可以有效地降低对PU 的干扰;当干扰概率一定时，带宽频谱感知可以提高次用户的频谱效率.

下一步将研究基于时间和带宽的二维频谱感知.

［1］ KRENIK W，BATRA A. Cognitive radio techniques for wide area networks［C］∥Design Automation Conference.Anaheim:IEEE，2005:409-412.

［2］ HAYKIN S. Cognitive radio:brain-empowered wireless communications［J］. IEEE Journal on Selected Areas in Communications，2005，23(2):201-220.

［3］ BOYD S W，FRYE J M，PURSLEY M B，et al.Spectrum monitoring during reception in dynamic spectrum access cognitive radio networks［J］. IEEE Transactions on Communications，2012，60(2):547-558.

［4］ LIU Xin，JIA Min，GU Xuemai，et al. Optimal periodic cooperative spectrum sensing based on weight fusion in cognitive radio networks［J］. Sensors，2013，13(4):5251-5272.

［5］ 刘鑫，谭学治，徐桂森. 噪声不确定下认知无线电能量检测性能的分析［J］. 四川大学学报:工程科学版，2011，43(6):168-172.LIU Xin，TAN Xuezhi，XU Guisen. Performance analysis of energy detection for cognitive radio under noise uncertainty［J］. Journal of Sichuan University:Engineering Science Edition，2011，43(6):168-172.

［6］ MARINHO J，MONTEIRO E. Cooperative sensingbefore-transmit in Ad-hoc multi-hop cognitive radio scenarios［C］∥International Conference on Wired Wireless Internet Communications. Santorini:Springer Verlag，2012:186-197.

［7］ 丁汉清，杨家玮，赵志远. 认知无线电系统中感知时间的优化［J］. 华中科技大学学报:自然科学版，2011，39(8):84-87.DING Hanqing， YANG Jiawei， ZHAO Zhiyuan.Optimization of sensing time in cognitive radio systems［J］. Journal of Huazhong University of Science and Technology: Natural Science Edition， 2011，39(8):84-87.

［8］ LIANG Y C，ZENG Y H，EDWARD C Y P，et al.Sensing-throughput tradeoff for cognitive radio networks［J］.IEEE Transactions on Wireless Communications，2008，7(4):1326-1336.

［9］ EDWARD C Y P， LIANG Y C， GUAN Y L.Optimization of cooperative sensing in cognitive radio networks:a sensing-throughput tradeoff view［J］. IEEE Transactions on Vehicular Technology，2009，58(9):5294-5299.

［10］ CHOI J K，YOO S J. Time-constrained detection probability and sensing parameter optimization in cognitive radio networks［J］. Eurasip Journal on Wireless Communications and Networking， 2013，20(1):1-12.

［11］ LIU Xin，TAN Xuezhi. Optimization for weighed cooperative spectrum sensing in cognitive radio network［J］. Applied Computational Electromagnetics Society Journal，2011，26(10):800-814.

［12］ PEH E C Y，LIANG Y C，GUAN Y L，et al.Cooperative spectrum sensing in cognitive radio networks with weighted decision fusion schemes［J］.IEEE Transactions on Wireless Communications，2010，9(12):3848-3857.

［13］ CHOI K W，JEON W S，JEONG D G. Adaptive and distributed access to spectrum holes in cognitive radio system［J］. Wireless Personal Communications，2013，70(1):207-226.

［14］ MA X，DJOUADI S M，LI H. State estimation over a semi-Markov model based cognitive radio system［J］.IEEE Transactions on Wireless Communications，2012，11(7):2391-2401.

［15］ ZHI Quan，SAYED A H，POOR H V. Optimal multiband joint detection for spectrum sensing in cognitive radio networks［J］. IEEE Transactions on Signal Processing，2009，57(3):1128-1140.

［16］ HATAMLOU A. In search of optimal centroids on data clustering using a binary search algorithm［J］. Pattern Recognition Letters，2012，33(13):1756-1760.