双缘COT 调制数字电压型控制Buck 变换器分析

周国华， 陈 兴， 崔恒丰

(西南交通大学电气工程学院，四川 成都610031)

近年来，随着数字控制器件和电力电子技术的飞速发展，电力电子设备的数字控制已经成为当今研究和讨论的热点话题. 与传统的模拟控制器相比，数字控制器只需修改软件里的程序就可调整控制算法，设计灵活［1］. 此外，数字控制器易于实现与其他数字设备之间的接口，从而具有较好的兼容性［2］.

开关电源的控制方法是影响其瞬态响应速度和稳压精度的重要因素.按照占空比的实现方式分类，其控制方法可以分为定频控制和变频控制［3-4］.定频控制指的是脉冲宽度调制(pulse width modulation，PWM)技术，变频控制指的是脉冲频率调制(pulse frequency modulation，PFM)技术. 文献［5］阐述了开关变换器调制方法与控制技术的本质特点，让工程设计人员与研究学者更加清晰地认识它们之间的区别和联系. PWM 是最常用的调制方法，能较好地调节开关变换器的输出，稳压精度高，但存在轻载效率低、响应速度慢和补偿网络设计复杂等缺点.相比于PWM，PFM 具有瞬态性能好、轻载效率高的优点，但稳压精度相对较差.

与定频控制相比，脉冲序列控制因其具有实现简单、瞬态响应速度快等优点，在开关电源中获得了广泛研究［6-7］.但是，脉冲序列控制开关变换器的输出电压纹波大、稳态性能差. 为了解决输出电压纹波较大这一问题，文献［7］提出了变脉宽脉冲序列控制技术. 恒定导通时间(constant on-time，COT)调制是PFM 调制技术之一［8］.为了提高COT调制开关变换器的稳压精度，文献［9-11］研究了数字V2-COT 控制技术，通过引入比例-积分环节改善了开关变换器的稳态性能，但使控制环路变得复杂.文献［12］采用双恒定导通时间控制技术，使得开关变换器获得了较高的稳压精度.本文以工作于电感电流连续导电模式(continuous conduction mode，CCM)的Buck 变换器为研究对象，提出了双缘恒定导通时间(dual-edge constant on time，DCOT)调制方法，对DCOT 调制数字电压型控制Buck 变换器的工作原理、稳态性能和瞬态性能进行了研究，并与传统COT 调制数字电压型控制Buck 变换器进行了对比分析. 最后，通过Matlab/Simulink 仿真软件和基于现场可编程门阵列(field programmable gate array，FPGA)的实验样机对理论分析进行了验证.

1 工作原理

图1 所示为COT 和DCOT 调制数字电压型控制Buck 变换器的电路原理框图和其工作波形. 其中，图1(a)为COT 和DCOT 调制数字电压型控制Buck 变换器的电路原理框图.图中，数字控制器包括模数转换器(analog to digital converter，ADC)、时间计算模块(time calculation module，TCM)和数字脉冲频率调制器(digital pulse frequency modulator，DPFM)，ug、uo和uref分别为输入电压、输出电压和基准电压，S1、S2分别为功率开关管、续流二极管，C、L 分别为输出电容、电感，Re为电容C 的等效串联电阻，R 为负载电阻. 在数字控制器中，Ton、Toff和Ts分别为预设的恒定导通时间、计算的关断时间和开关周期，VP、Sclk分别为开关管驱动信号、ADC 采样信号.

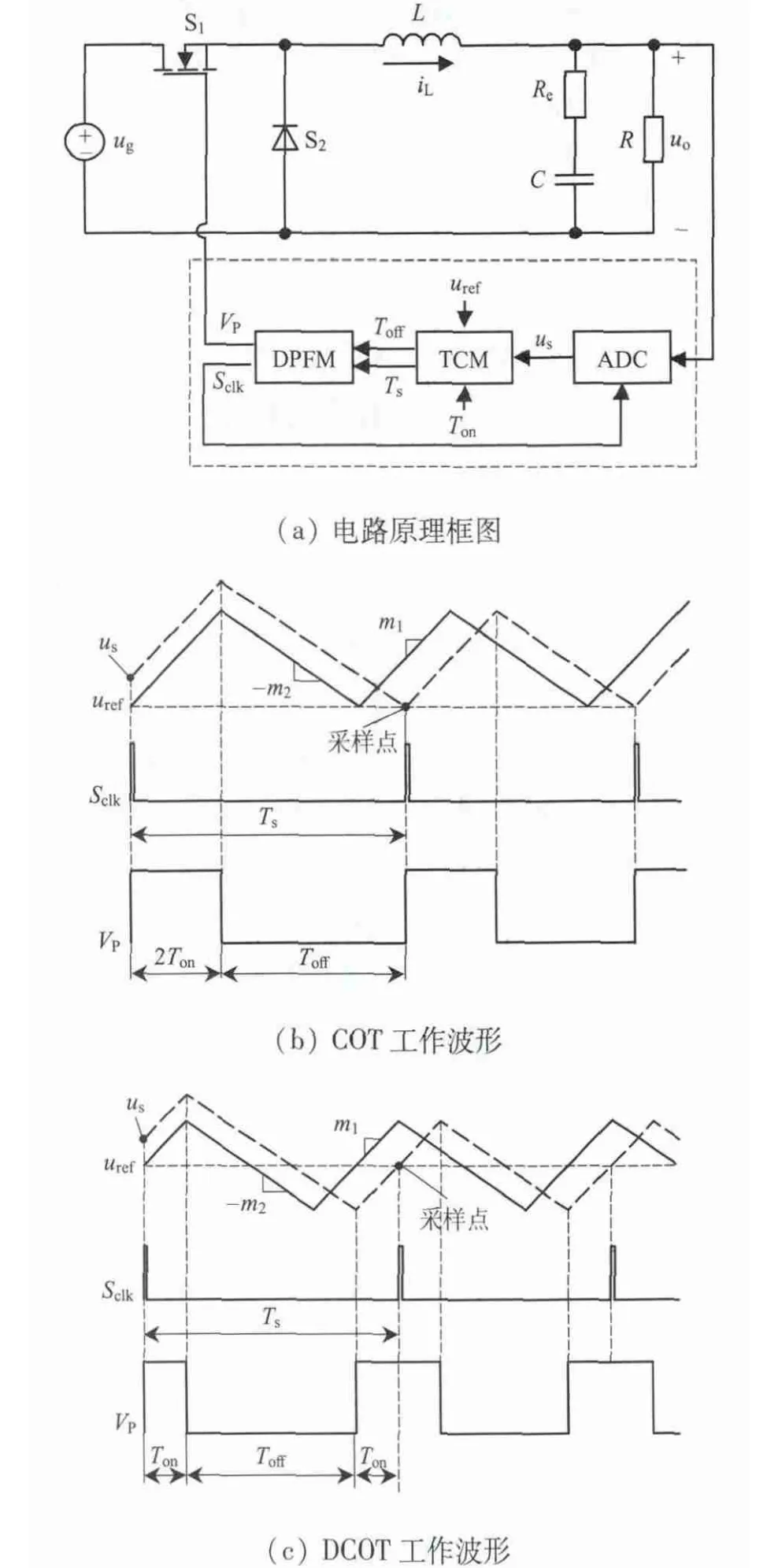
图1 COT 和DCOT 调制数字电压型控制Buck 变换器Fig.1 Digital voltage-mode controlled Buck converter with COT and DCOT modulations

图1(b)所示为CCM模式下传统COT调制数字电压型控制Buck 变换器在两个相邻开关周期的工作波形.图中，m1和m2分别为输出电压纹波的上升斜率和下降斜率，实线为稳态波形，虚划线为扰动后输出电压重新返回到稳态的调整波形.在每个开关周期起始时刻，采样信号Sclk使能ADC，对输出电压进行采样，采样值记为us;同时，DPFM 使VP输出高电平，控制开关管S1导通，导通时间为预设的2Ton. 在开关管S1导通期间，根据us、uref、m1、m2在TCM 内计算出关断时间Toff;开关管S1导通结束后，DPFM 使VP输出低电平，控制开关管S1关断，关断时间为计算出来的Toff. 当开关管S1关断结束后，Sclk再次使能ADC 对输出电压进行采样，进入下一个开关周期.

图1(c)所示为CCM 模式下DCOT 调制数字电压型控制Buck 变换器的工作波形. 在每个开关周期起始时刻，采样信号Sclk使能ADC 对输出电压进行采样，同时，DPFM 控制开关管S1导通，导通时间为预设的Ton，导通期间在TCM 中计算Toff.开关管S1导通结束后，VP输出低电平，开关管S1关断，关断时间为Toff.之后，开关管S1再次导通Ton，直至当前开关周期结束.

2 性能分析

2.1 稳态性能分析

由第1 节中的工作原理分析可知，传统COT调制和DCOT 调制在每个开关周期内的导通时间相同，不同之处在于导通时间的位置分布. 当传统COT 调制和DCOT 调制数字电压型控制Buck 变换器工作于稳态时，在一个开关周期结束时刻的输出电压分别为

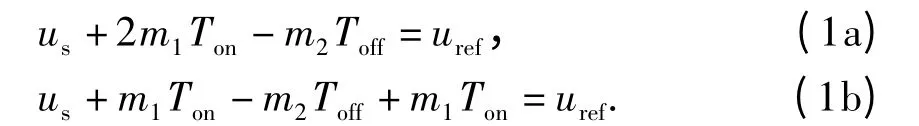
当输出电容的等效串联电阻Re较大时，Buck变换器的输出电压纹波表现为Re上的纹波，呈线性变化;当Re很小时，输出电压纹波是非线性的，COT 调制和DCOT 调制数字电压型控制Buck 变换器都不能正常工作，这与COT 控制Buck 变换器一致［13］.本文只考虑Re较大的情形，此时，图1(b)和图1(c)中的斜率m1和m2可分别表示为［14］

由式(1)可得

考虑恒定导通时间，进一步可得

通过上述分析可知，当ADC 采样输出电压的值即us相同时，采用COT 调制和DCOT 调制方法计算出的Toff和Ts是相同的.

传统COT 调制可称为单缘恒定导通时间调制，其本质上是将输出电压的谷值稳定在基准电压uref，导致输出电压的均值始终大于基准电压，因而稳压精度较差.而DCOT 调制，实质上是通过在每个开关周期的起始段和结束段各导通相等的恒定导通时间，其大小为传统COT 调制中恒定导通时间的一半，并将输出电压的均值稳定在基准电压uref.与传统COT 调制相比，DCOT 调制称为双缘恒定导通时间调制，提高了输出电压的稳压精度，从而使数字电压型控制Buck 变换器具有很好的稳态性能.

2.2 瞬态性能分析

图2(a)所示为COT 调制数字电压型控制Buck 变换器在第N 个开关周期的区间［(N-1)Ts，(N-1)Ts+Ton］内发生负载加载的瞬态波形，即在输出电压纹波谷值处到输出电压纹波上升阶段中点处的这个范围内发生负载突变. 从图2(a)可以看出，负载突变点位于采样点之后，此时虽然负载发生了突变，但由于当前开关周期的采样动作已经结束，导致当前开关周期的关断时间Toff不能及时被更新，必须等到下一个开关周期采样输出电压后重新计算关断时间，Toff才会被更新，瞬态调节过程滞后.

图2(b)所示为DCOT 调制数字电压型控制Buck 变换器在第N - 1 个开关周期的区间［(N-1)Ts-Ton，(N-1)Ts］内发生负载加载的瞬态波形. 从图2(b)可以看出，负载突变的区间［(N-1)Ts-Ton，(N-1)Ts］属于第N 个开关周期采样点之前，即将进行采样动作，能够及时更新关断时间，从而能够较快地调节输出电压.

对比图2(a)中第N 个开关周期区间［(N-1)Ts，(N-1)Ts+ Ton］的输出电压波形与图2(b)中第N-1 个开关周期区间［(N-1)Ts-Ton，(N-1)Ts］的输出电压波形可知，两者是相互对应的，因此，可以将其统一规定为区间［(N-1)Ts，(N-1)Ts+Ton］.当传统COT 调制与DCOT 调制在区间［(N-1)Ts，(N-1)Ts+Ton］发生负载减载时，关断时间Toff的更新与负载加载时相同.

通过上述分析可知，当负载在区间［(N-1)Ts，(N-1)Ts+Ton］发生突变时，相比于传统COT 调制数字电压型控制Buck 变换器，DCOT 调制数字电压型控制Buck 变换器的瞬态性能更好. 而在其他区间发生负载突变时，COT 调制与DCOT 调制的负载突变点距离下一次采样点的时间相同，所以瞬态性能一致.

图2 两种调制方式下发生负载突变后的瞬态波形Fig.2 Transient waveforms for two modulations under load variation

3 仿真研究

为了比较传统COT 调制与DCOT 调制数字电压型控制算法的性能，采用Matlab/Simulink 仿真软件，选取表1 所示的电路参数对COT 和DCOT调制数字电压型控制CCM Buck 变换器进行了时域仿真，对比分析了它们的稳态性能和瞬态性能.

表1 数字电压型控制Buck 变换器参数Tab.1 The parameters of digital voltage-mode controlled Buck converter

图3 给出了COT 和DCOT 调制数字电压型控制CCM Buck 变换器的稳态仿真波形.从图3 可以看出，COT 调制和DCOT 调制数字电压型控制Buck 变换器的电感电流均大于0，表明变换器工作于CCM，前者的输出纹波电压平均值与基准电压uref存在一定的正偏移量，其大小为输出电压纹波峰峰值的50%，后者的输出纹波电压平均值与uref相同.因此，相比于传统COT 调制，DCOT 调制的数字电压型控制Buck 变换器的输出电压的稳压精度提高了输出电压纹波峰峰值的50%.

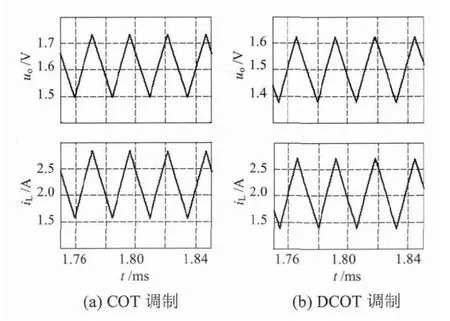
图3 COT 和DCOT 调制数字电压型控制CCM Buck 变换器的稳态仿真波形Fig.3 The steady-state simulation waveforms of digital voltage-mode controlled Buck converter in CCM with COT and DCOT modulations

图4 为负载在区间［(N -1)Ts，(N -1)Ts+Ton］发生加载(1 A→2 A)的瞬态仿真波形.

图4 负载在区间［(N-1)Ts，(N-1)Ts +Ton］加载的瞬态仿真波形Fig.4 Transient simulation waveforms under load increasing in ［(N-1)Ts，(N-1)Ts +Ton］

由图4 可知，负载在区间［(N-1)Ts，(N-1)Ts+Ton］发生跳变后，传统COT 调制数字电压型控制Buck 变换器的瞬态调节要比DCOT 调制数字电压型控制Buck 变换器的瞬态调节多1 个开关周期，调节时间增加了1 倍左右.

图5 为负载在区间［(N -1)Ts+Ton，NTs］发生加载(1 A→2 A)的瞬态仿真波形. 由图5 可以看出，负载在区间［(N-1)Ts+Ton，NTs］发生跳变后，COT 调制与DCOT 调制数字电压型控制Buck变换器的瞬态调节时间基本相同，与理论相吻合.

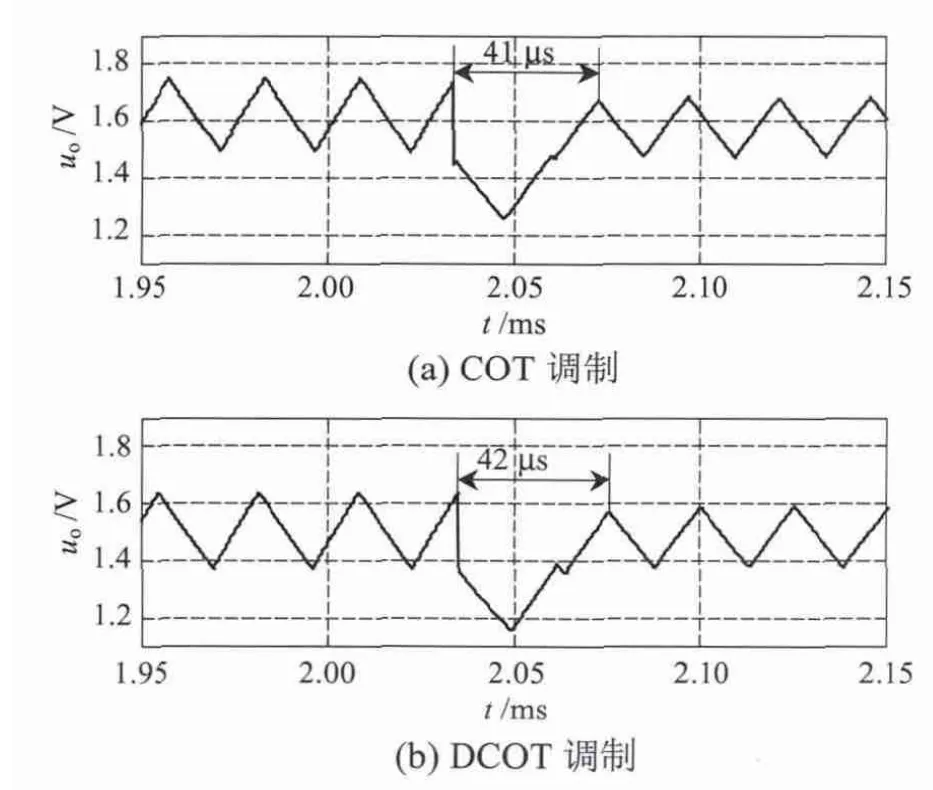
图5 负载在区间［(N-1)Ts +Ton，NTs］加载的瞬态仿真波形Fig.5 Transient simulation waveforms under load increasing in ［(N-1)Ts +Ton，NTs］

4 实验验证

为了验证理论分析和仿真结果的正确性，采用表1 所示的电路参数，建立了基于FPGA 的数字控制实验平台，其中FPGA采用芯片为Xilinx公司生产的Spartan6xc6slx9，系统时钟为50 MHz，采用ADC 芯片为AD9226，最大(采样)转换速率为65 Msps.

DCOT 调制的数字实现如图6 所示. DPFM 从0 开始计数产生数字调制波Vsaw，在Vsaw达到式(4)计算出的Ts时开关周期结束. 设置常数Cclk为1，并将其与Vsaw进行比较，产生采样脉冲信号Sclk，控制ADC 对输出电压进行采样. 根据恒定导通时间Ton和计算出的关断时间Toff与Vsaw相比较，产生期望的VP输出. 当Ton＞Vsaw，VP输出高电平，使功率开关管S1导通;当Ton≤Vsaw≤Ton+Toff时，VP输出低电平，使功率开关管S1关断;当Ton+Toff＞Vsaw时，VP输出高电平，使功率开关管S1导通.

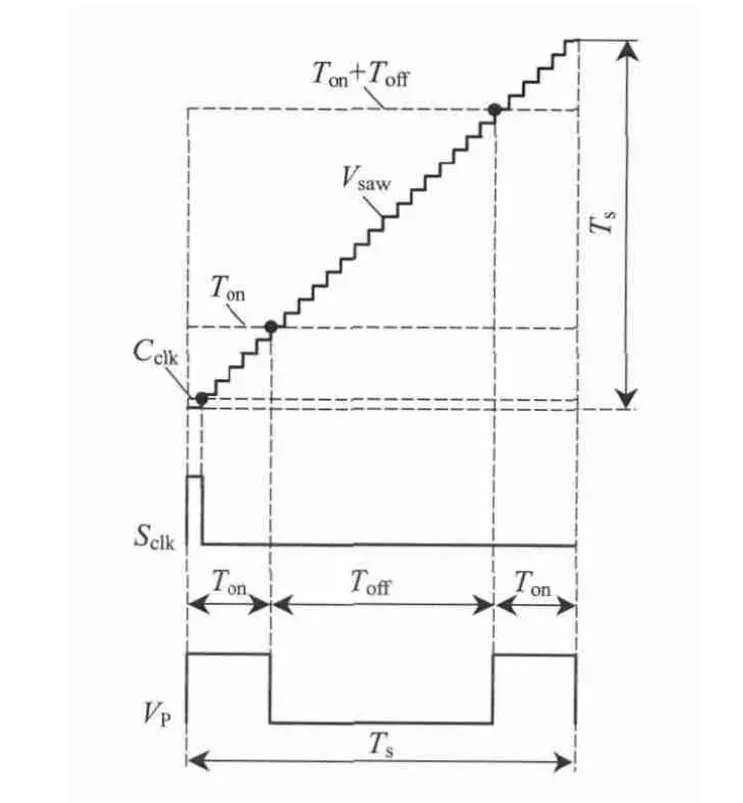
图6 DCOT 调制的数字实现Fig.6 Illustration of DCFT modulation with digital implementation

图7 给出了两种调制方式下数字电压型控制Buck 变换器的实验波形.

图7 COT 和DCOT 调制数字电压型控制CCM Buck 变换器的稳态实验波形Fig.7 The steady-state experiment waveforms of digital voltage-mode controlled Buck converter inCCM with COT and DCOT modulations

从图7 可以看出，COT 调制的输出电压谷值在基准电压处，而DCOT 调制的输出电压均值在基准电压处;两者的电感电流均大于0，说明变换器工作于CCM. 图7 所示的实验结果验证了DCOT 调制的稳压精度优于COT 调制.

图8、图9 分别为负载在区间［(N - 1)Ts，(N-1)Ts+Ton］发 生 加 载(1 A →2 A)、减 载(2 A→1 A)的瞬态实验波形.

图8 负载在区间［(N-1)Ts，(N-1)Ts +Ton］加载的瞬态实验波形Fig.8 Transient experiment waveforms under load increasing in ［(N-1)Ts，(N-1)Ts +Ton］

图9 负载在区间［(N-1)Ts，(N-1)Ts +Ton］减载的瞬态实验波形Fig.9 Transient experiment waveforms under load decreasing in ［(N-1)Ts，(N-1)Ts +Ton］

从图8、图9 可以看出，负载加载时，COT 调制方式下的瞬态调节时间为42 μs，而DCOT 调制仅需20 μs;负载减载时，COT 调制方式下的瞬态调节时间为47 μs，而DCOT 调制仅需25 μs.图8 和图9 的实验结果验证了负载在区间［(N-1)Ts，(N-1)Ts+Ton］跳变时，DCOT 调制的瞬态性能优于COT 调制.

图10、图11 分别为负载在［Ton+(N -1)Ts，NTs］发生加载(1 A→2 A)、减载(2 A→1 A)的瞬态实验波形. 从图10、图11 可以看出，负载加载时，COT 调制和DCOT 调制的瞬态调节时间分别是42 和41 μs;负载减载时，COT 调制和DCOT 调制的瞬态调节时间分别是47 和48 μs.

图10 和图11 的实验结果验证了负载在区间［Ton+(N-1)Ts，NTs］跳变时，DCOT 调制的瞬态性能与COT 调制相同.

文献［15］指出实际工作中电感值的变化，电容的等效串联电阻变化对数字控制算法具有很好的鲁棒性或参数容忍性，对数字控制变换器的性能影响不大.而从图8 ～11 的实验结果可以看出，负载跳变后，传统COT 和DCOT 的稳压精度均发生了改变，这是由于实际电路中开关管、电感存在寄生电阻造成的.当负载发生变化时，线路中的电流也随之发生改变，从而在寄生电阻上产生的电压也发生了变化，造成电感电流上升斜率与下降斜率发生改变，进而使得实际输出电压的上升斜率和下降斜率与算法(3)中固定的m1、m2不一致，从而影响了计算关断时间的精确度，所以稳压精度会受到影响.为了降低这种影响，可以在算法(3)中采用变化的m1、m2，这将是笔者下一步的研究工作.

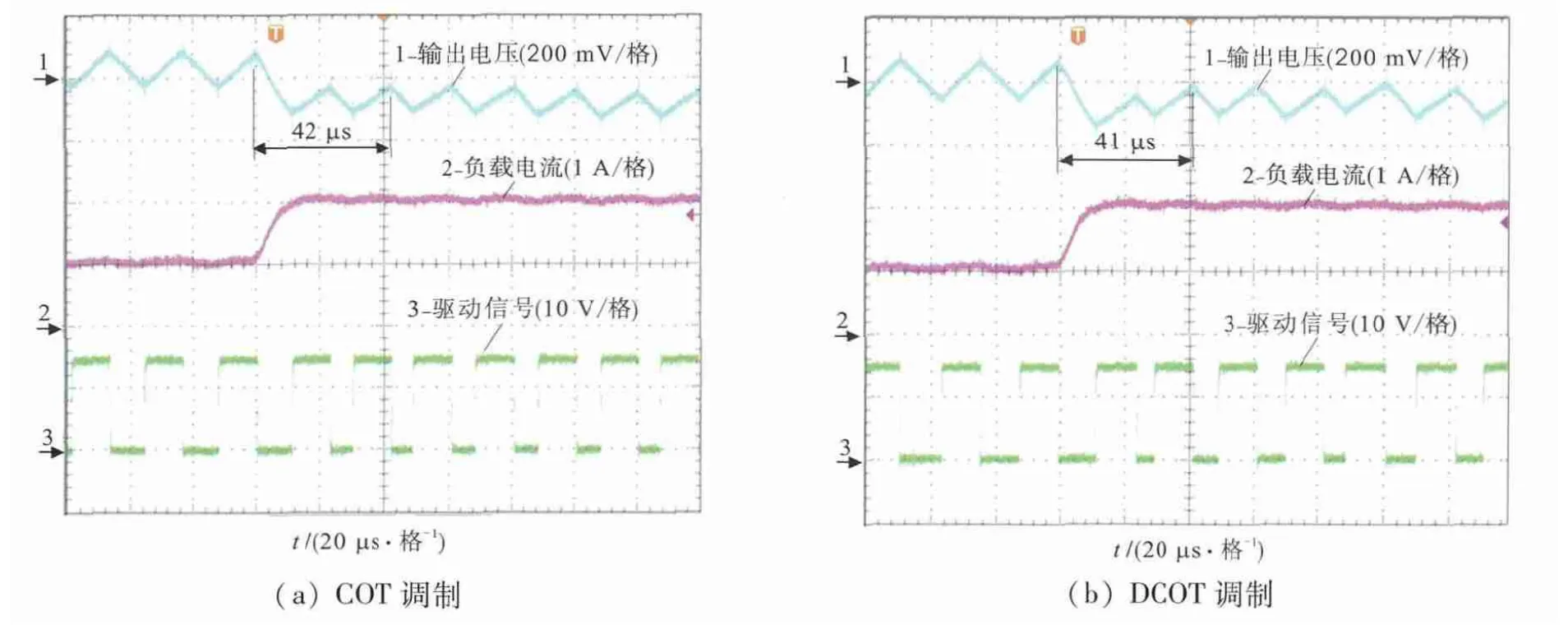
图10 负载在区间［(N-1)Ts +Ton，NTs］加载的瞬态实验波形Fig.10 Transient simulation waveforms under load increasing in ［(N-1)Ts +Ton，NTs］

图11 负载在区间［(N-1)Ts +Ton，NTs］减载的瞬态实验波形Fig.11 Transient simulation waveforms under load decreasing in ［(N-1)Ts +Ton，NTs］

5 结 论

本文以工作于CCM 的Buck 变换器为研究对象，详细介绍了DCOT 调制和COT 调制技术，对比分析了两种调制技术下固定导通时间与关断时间的关系，以及两种调制方式下数字电压型控制Buck 变换器的稳态性能和瞬态性能. 理论分析与仿真研究均表明:与COT 调制相比，DCOT 调制的稳压精度要高;负载在区间［(N-1)Ts，(N-1)Ts+Ton］突变时，DCOT 调制的瞬态性能要更好;负载在其他区间突变时，两者的瞬态性能基本一致.最后，采用基于FPGA 的实验平台，对理论分析和仿真结果进行了验证.

［1］ 周涛. 高频开关电源数字控制技术研究［D］. 成都:西南交通大学，2006.

［2］ 周国华，许建平. 开关变换器数字控制技术［M］. 北京:科学出版社，2011:6-7.

［3］ 王凤岩，许峻峰，许建平. 开关电源控制方法综述［J］. 机车电传动，2006(1):6-10.WANG Fengyan，XU Junfeng，XU Jianping. Survey on control methods of switching power supply［J］. Electric Drive for Locomotives，2006(1):6-10.

［4］ 陈亚爱，张卫平，周京华，等. 开关变换器控制技术综述［J］. 电气应用，2008，27(4):4-10.CHEN Yaai，ZHANG Weiping，ZHOU Jinghua，et al. A review of control techniques for switching converters［J］.Electrotechnical Application，2008，27(4):4-10.

［5］ 周国华，许建平. 开关变换器调制与控制技术综述［J］. 中国电机工程学报，2014，34(6):815-831.ZHOU Guohua，XU Jianping. A review of modulation and control techniques for switching converters［J］.Proceedings of the CSEE，2014，34(6):815-831.

［6］ 秦明，许建平，牟清波. 脉冲序列Buck 变换器的控制规律及特性［J］. 西南交通大学学报，2009，44(5):660-666.QIN Ming，XU Jianping，MU Qingbo. Control laws and characters of pulse train controlled Buck converters［J］.Journal of Southwest Jiaotong University，2009，44(5):660-666.

［7］ 吴松荣，钟曙，许建平，等. 变脉宽脉冲序列控制DCM Buck 变换器［J］. 西南交通大学学报，2014，49(3):455-461.WU Songrong，ZHONG Shu，XU Jianping，et al.Variable width pulse train controlled DCM Buck converter［J］. Journal of Southwest Jiaotong University，2014，49(3):455-461.

［8］ PRIEWASSER R，AGOSTINELLI M，UNTERRIEDER C，et al. Modeling，control and implementation of DC-DC converters for variable frequency operation［J］. IEEE Transactions on Power Electronics，2014，29(1):287-301.

［9］ CHENG K Y，YU F，LEE F C，et al. Digital enhanced V2-type constant on-time control using inductor current ramp estimation for a Buck converter with low-ESR capacitors［J］. IEEE Transactions on Power Electronics，2013，28(3):1241-1252.

［10］ YU F，LEE F C. Design oriented model for constant ontime V2control［C］∥Energy Conversion Congress and Exposition (ECCE). Atlanta:IEEE，2010:3115-3122.

［11］ 金艳艳. 开关电源脉冲频率调制数字V2控制技术研究［D］. 成都:西南交通大学，2011.

［12］ ZHOU Guohua，CHEN Xing，CUI Hengfeng，et al.High output-regulation accuracy and fast transient response of dual constant on-time controlled switching converter［J］. Electronics Letters，2014，50(7):543-545.

［13］ WANG Jinping，XU Jianping，BAO Bocheng. Analysis of pulse bursting phenomenon in constant-on-timecontrolled Buck converter［J］. IEEE Transactions on Industrial Electronics，2011，58(12):5406-5410.

［14］ ERICKSON R W，MAKSIMOVIC D. Fundamentals of Power Electronics［M］. 2nd ed. Norwell:Kluwer，2001:15-22.

［15］ ZHOU Guohua，XU Jianping，ZHANG Fei. Unified pulse-width modulation scheme for improved digitalpeak-voltage control of switching DC-DC converters［J］.International Journal of Circuit Theory and Applications，2014，42(7):671-686.