电气化高速铁路接触网微风振动特性

刘志刚， 宋 洋， 刘煜铖

(西南交通大学电气工程学院，四川 成都610031)

输电线微风振动是一种柔性结构物的风振现象.微风振动振幅一般不超过导线直径的2 ～3 倍，该现象频繁发生，持续时间长，可导致导线疲劳断股以及相关配件、设备、杆塔构件的损坏，限制了输电线的使用寿命［1］.因此，输电线的微风振动一直是国际上普遍关心的课题.文献［2］分析了输电线的气动功率测量与涡激振动现象;文献［3］进行了输电线微风振动的实时测量研究;文献［4］利用多阻尼方法提出了一种研究单导线微风振动的算法;文献［5］针对1 000 kV 特高压架空输电线路，研究了利用有限元方法分析微风振动方法.与输电线相比，接触网具有系统结构复杂、跨距段短、承力索和接触线张力大的特点，其微风振动与输电线有明显的不同.国内论文偏重于接触线舞动现象的讨论，如文献［6-8］为定性分析;国外论文偏重于气动特性的分析，如文献［9］分析了弓网相互耦合下的受电弓气动性能，文献［10-12］对接触线的气动力特性进行分析，并用邓哈托垂直振动理论判断其气动稳定性.

本论文针对水平风下电气化高速铁路接触网垂直方向上的微风振动，结合动力学方法进行微风振动公式推导和仿真.首先通过接触网水平风激励下的受力分析，推导出承力索和接触线在风激励下的振动方程;接着基于接触网的动力学方程，求解出接触网的固有频率;最后推导出承力索和接触线随接触网固有频率变化的微风激振力公式，分析接触网的微风振动现象.

1 接触网微风振动现象

当风吹过圆柱体时，在圆柱体的背风侧形成上下方向交替变化的气流漩涡，并不断地以一定速度离开圆柱体，向后面延伸而渐渐消失. 由于上下交替产生漩涡，在圆柱体上作用上下交替的力，使其上下振动，这种现象称为卡门涡街(Karman vortex street).Strouhal 发现当出现振动时，漩涡有比较稳定的频率fS，即Strouhal 频率或冲击频率，计算式［1］为

式中:V 为流体的速度;D 为圆柱体的直径;S 为Strouhal 数.

当漩涡脱落频率与系统的固有频率一致时，引起谐振，使作用于圆柱体上的交变冲击力变大，激发圆柱体产生较大振幅的振动.当圆柱体以此频率振动后，圆柱体背风侧的漩涡出现频率不变，当风速在一定范围变化时，圆柱体的振动频率和漩涡的频率保持不变，这种现象为“锁定效应”［13］.该现象发生是因为振动的圆柱体控制了气流中形成漩涡的频率.接触线的形状类似圆柱，当风吹过时，也会在其背面形成稳定的漩涡，图1 为接触线在CFD(computational fluid dynamics)中形成的卡门涡街，能够清楚地看到漩涡的脱落.

图1 接触线的卡门涡街现象Fig.1 Karman vortex street of catenary

当涡街的脱落频率与接触网的固有频率一致时，会引起接触网系统的共振，可导致接触网疲劳断裂、弓网受流变差等一系列后果.

2 接触网水平风下的振动方程

在分析接触网的微风振动时，首先需要推导出接触网水平风下的振动方程.

将接触线和承力索看作欧拉-伯努力梁，做如下简化:

(1)仅讨论接触网垂直方向的振动;

(2)与承力索和接触导线相比吊弦线质量很小，将吊弦的质量平分到吊弦两端的线夹上，吊弦简化为两端为几种质量、中间为弹簧的弹簧质量系统;

(3)支撑杆简化为一个单自由度的弹簧质量系统，不考虑横向振动，限位器可简化为附加于接触网上的质量;

(4)在接触线或承力索上取一段长度dx 的单元［14］，如图2 所示.

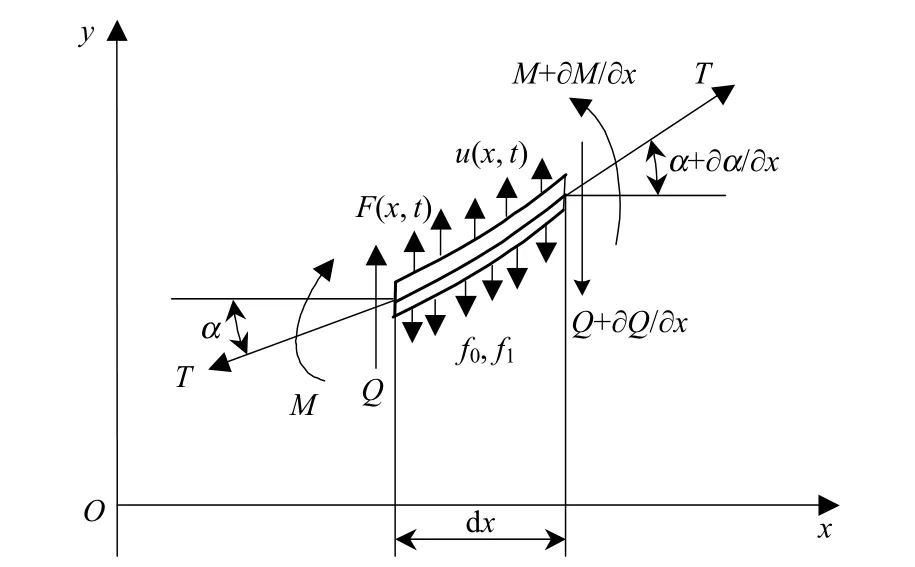
图2 水平风下接触线微分段受力图Fig.2 Micro-segment forces under horizontal wind

根据力平衡原理，垂直方向投影力之和为0，

式中:ρ 为其单位长度质量;

t 为时间;

F(x，t)为水平风产生的垂直激励力;

u(x，t)为微分段受吊弦的拉力;

y(x，t)为承力索/接触线在竖直方向上所产生的位移;

ρgdx 为微分段自身的重力;

f0为在垂直方向运动时承力索/接触线自身所具有的阻尼力;

Q 为微分段两端的剪力;

M 为弯矩;f1为惯性力;f1dx 为横向惯性力，其值为该微分段质量和加速度的乘积.

在研究轴向力时，主要应考虑张力T 及剪力的影响，有平衡方程

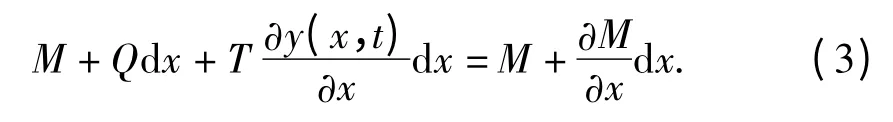
式中:EI 为接触线/承力索微分段抗弯强度.

导线在风激励时吊弦拉力和重力可以近似相等，吊弦拉力u(x，t)和自身重力ρg 在承力索/接触线的振动方程中可忽略，则式(3)为具有一定刚度的承力索/接触线受风激励和吊弦拉力的振动微分方程，其齐次方程为

式(5)可用分离变量分解法［15］求解，得

式中:

X(x)为广义坐标;

T(t)为振型函数.

式中:xr为承力索/接触线上的集中载荷点的坐标，下标r 为集中载荷点的个数;

ωm为接触线/承力索的自振频率.

式(7)为水平风下承力索/接触线的微分振动方程.

若用An和Bn分别代表承力索和接触线振动各阶的幅值，并代入式(7)，可求得承力索和接触线的第n 阶运动微分方程式(9)和式(10)，

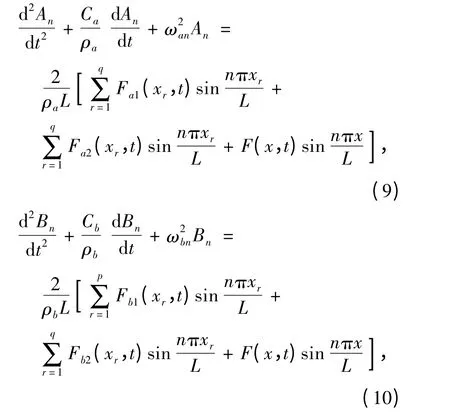
式中:

Fa1(xr，t)、Fa2(xr，t)分别为吊弦和支撑杆对承力索的集中力;

Fb1(xr，t)、Fb2(xr，t)分别为吊弦和定位器对接触线的集中力;

F(x，t)为水平风产生的垂直激励力;

ρa、ρb分别为承力索和接触线的单位质量;

Ca、Cb分别为承力索和接触线的阻尼系数;

EIa、EIb分别为承力索和接触线的刚度;

Ta、Tb分别为承力索和接触线的张力;

p 为吊弦个数;

q 为支撑杆或者定位器的个数.

考虑吊弦对承力索的集中力，mDr、KDr分别为吊弦的质量和刚度，支撑杆对承力索的集中力;mAr、KAr分别为支撑杆的质量和刚度，吊弦对接触线的集中力;定位器对接触线的集中力;mBr为定位器质量.联立承力索和接触线的微分振动方程，以及吊弦、定位器、支撑杆的集中力，可推导得

式(11)和式(12)分别为承力索和接触线在风激励F(x，t)下的振动方程.

3 接触网固有频率计算

获得接触网的风激励下的振动方程后，需要与接触网本身的固有频率进行比较，以求出发生共振时的公式. 以欧洲标准EN50318 中的标准模型作为算例，求垂直平面内的固有频率.

接触网参数如表1 所示.

接触线或承力索任意一点的位移可表示为

式中:φ(x)为振型函数;

q(t)为式(10)和式(11)中的广义位移An和Bn，q(t)随三角函数规律变化，则

式中:r 为广义幅值对应的振幅;

i 为虚数单位;

ω 为角频率.

表1 EN50318 标准模型接触网基本参数Tab.1 Basic parameters of catenary in EN50318 standard

将式(14)代入式(13)，得

y(x，t)=reiωtφ(x)，

其中，y0=rφ(x)是随x 变化的广义幅值.

将q(t)=reiωt带入接触网风激励下的运动微分方程式(11)和式(12)，即

An=raneiωt， Bn=rbneiωt，

可以得到

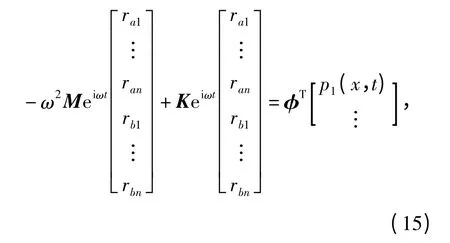
式中:ran、rbn分别为承力索和接触线第n 阶模态的广义幅值对应的振幅;

p1(x，t)为每一个微分段节点的微风激振力;

φT为振型矩阵的逆矩阵;

M、K 分别为整体质量和刚度矩阵.

整理式(15)可得

利用Landczos 法求解上述动力学方程的特征方程，可得到接触网n 阶固有频率. 部分固有频率下的振型如图3 所示，前10 阶的固有频率如表2所示.从表2 中可以看出，系统的最低固有频率为0.965 Hz.另外，在低频区域，固有频率比较密集，第50 阶时，接触网的固有频率也只有10 Hz，因此，接触网系统是一个低频振动系统.

图3 不同频率下的接触网振型Fig.3 Vibration modes of catenary at different frequencies

表2 接触网前10 阶固有频率Tab.2 The first 10 order natural frequencies of catenary

4 接触网的微风振动分析

当卡门涡街脱落频率与接触网某阶固有频率一致时，可能会导致接触网一定振幅的共振，对接触网自身的疲劳强度和受流都会产生不利的影响.由于接触悬挂的特殊性，要产生整体的共振，必须要在承力索和接触网都产生与接触网某阶固有频率相同的微风激振力. 接触网整体发生微风振动时，承力索和接触线将随接触网某阶固有频率变化产生微风激振力，该力可表示为

式中:FL为气动升力，

其中:CL为接触网线索升力系数;

Lu为线索单元长度;

u 为风速;

ρair为空气密度;

D 为线索直径.

风洞试验获得攻角为90°的升力系数值在1.4 ～1.9 之间，这里取折中值1.7.将式(17)带入式(15)，可解出接触网在微风激振力作用下不同频率的振幅.例如:对于接触线，当固有角频率为13.567 rad/s时，接触线的振幅变化如图4(a)所示;当固有角频率为313.44 rad/s 时，接触线的振幅变化如图4(b)所示;当固有角频率为1 515.5 rad/s 时，接触线的振幅变化如图4(c)所示.

图4 不同角频率下接触线振幅变化Fig.4 Amplitude changes of catenary at different angle frequencies

根据接触线的振幅变化，可以发现不同固有频率对接触线产生的微风振动是不一样的，可以找出接触线不同频率下的最大振幅，如图5 所示.

由图5 可以看出，接触线振动的最大幅值一般在1 mm 以内，振幅最大点出现在角频率为131.1 rad/s处，振动的最大幅值达到0.96 mm，对应的风速为1.44 m/s.

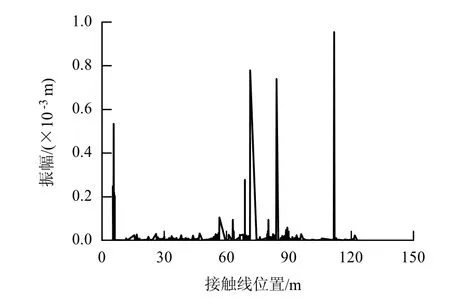
图5 接触线不同频率下的最大振幅Fig.5 Maximum amplitude of catenary at different frequencies

5 结束语

论文通过推导接触网垂直方向上的微风振动公式，求解出接触网的固有频率，获得接触网在微风振动作用下不同频率的振幅. 计算结果表明，在风速为1.44 m/s 左右，接触线微风振动的最大幅值达到0.96 mm，对应的角频率为131.1 rad/s.因此，由漩涡脱落引起的接触线微风振动振幅很小，不会产生输电线类似的振幅，不会对电气化铁路的实际运营造成显著影响.

［1］ 郭应龙，李国兴，尤传永. 输电线路舞动［M］. 北京:中国电力出版社，2003:3-24.

［2］ SIMMONS J M， CLEARY P M. Measurement of aerodynamic power associated with vortex induced vibration of electrical transmission lines［J］. IEEE Transactions on Power Apparatus and Systems，1980，99(l):158-164.

［3］ GODARD B，GURARD S，LILIEN J L. Original realtime observations of aeolian vibrations on power-line conductors［J］. IEEE Transactions on Power Delivery，2011，26(4):2111-2117.

［4］ LU M L，CHAN J K. An efficient algorithm for aeolian vibration of single conductor with multiple dampers［J］.IEEE Transactions on Power Delivery，2007，22(3):1822-1829.

［5］ 孔德怡，李黎，龙晓鸿，等. 特高压架空输电线微风振动有限元分析［J］. 振动与冲击，2007，26(8):64-67.KONG Deyi，LI Li，LONG Xiaohong，et al. Analysis of aeolian vibration of UHV transmission conductor by finite element method［J］. Journal of Vibration and Shock，2007，26(8):64-67.

［6］ 班瑞平. 接触网线索舞动现象的研究［J］. 铁道机车车辆，2004，24(1):64-66.BAN Ruiping. Research on phenomena of the contact line brandishing［J］. Railway Locomotive ＆ Car，2004，24(1):64-66.

［7］ 姚康佛. 接触网导线发生自由振动的原因及预防措施［J］. 电气化铁道，1999(4):31-33.YAO Kangfo. Catenary wire free vibration occurs causes and preventive measures［J］. Electrified Railway，1999(4):31-33.

［8］ 孟祥奎. 接触网振动分析及防振措施［J］. 电气化铁道，2003(4):16-18.MENG Xiangkui. Catenary vibration analysis and antivibration measures［J］. Electrified Railway，2003(4):16-18.

［9］ BOCCIOLONE M，RESTA F，ROCCHI D，et al.Pantograph aerodynamic effects on the pantograph catenary interaction［J］. Vehicle System Dynamics，2006，44(Sup.1):560-570.

［10］ STICKLAND M T，SCANLON T J. An investigation into the aerodynamic characteristics of catenary contact wires in a cross-wind［J］. Proceedings of the Institution of Mechanical Engineers Part F:Journal of Rail and Rapid Transit，2001，215(4):311-318.

［11］ STICKLAND M T，SCANLON T J，CRAIGHEAD I A，et al. An investigation into the mechanical damping characteristics of catenary contact wires and their effect on aerodynamic galloping instability［J］. Journal of Rail and Rapid Transit，2003，217(2):63-71.

［12］ SCANLON T J，STICKLAND M T，OLDROYD A B.Investigation into the attenuation of wind speed by the use of windbreaks in the vicinity of overhead wires［J］. Journal of Rail and Rapid Transit，2000，214(4):173-182.

［13］ 李黎，叶志雄，孔德怡. 输电线微风振动分析方法能量平衡法的改进研究［J］. 工程力学，2009，26(增刊1):176-180，197.LI Li，YE Zhixiong，KONG Deyi. Improvement of energy balance method and analysis of Aeolian vibration on UHV transmission lines［J］. Engineering Mechanics，2009，26(Sup.1):176-180，197.

［14］ 李丰良，李敏，唐建湘. 重力影响下的接触网运动微分方程［J］. 中南大学学报:自然科学版，2005，36(4):673-677.LI Fengliang，LI Min，TANG Jianxiang. Differential equations of catenary motion influenced by gravity［J］.Journal of Central South University:Natural Science，2005，36(4):673-677.

［15］ 谢官模. 振动力学［M］. 北京:国防工业出版社，2011:32-47.