冻土蠕变的非线性模型研究
2015-01-12项蒙佳赵少飞
曹 伟,项蒙佳,赵少飞
(华北科技学院 土木工程系,北京 东燕郊 101601)
0 引言
目前,人们对资源的需求急剧增加,必须加大对深部资源的开采,然而对深部资源的开采通常需要穿越软土层或者地下水丰富的土层,这就需要采用人工冻结的方法去解决实际的工程问题。由于冰和未冻水的存在,冻土在恒荷载作用下会发生蠕变,尤其在高应力水平下会进入加速蠕变阶段并迅速破坏,因而传统基于弹性和弹塑性理论计算的结果已经不再适用,在冻土的本构关系中应该考虑时间和应力水平的影响,并且模型应能描述冻土的整个流变过程包括加速蠕变阶段。
流变模型是研究岩土材料蠕变特性的一种常用方法,经典的模型有开尔文模型、伯格斯模型、宾汉姆模型及西原模型等。汪仁和等[1-3]对现有的流变模型进行分析,并通过大量的冻土单轴蠕变试验,用非线性牛顿体代替线性牛顿体,改进了西原模型,并添加到了ADINA程序中,后来又基于统计损伤理论,对西原模型中的弹塑性变量进行修正,建立了冻土蠕变损伤本构模型。毛芬和姚兆明[4]考虑了时间因素,采用非定常开尔文模型更好地描述了冻土的蠕变规律,非定常开尔文模型是研究冻土蠕变规律的新思路。蔡永刚和张秀娥[5]对西原模型进行了改进,用改进的开尔文模型来描述岩石蠕变的前两个阶段,用一种新的黏塑性体来描述岩石蠕变的第三个阶段,所建立的模型较为合理。袁文华[6]在西原模型中加入一黏弹性元件项,以抛物线屈服函数替代塑性屈服项,建立了高应力下抛物线型黏弹塑性蠕变本构模型。陈军浩等[7]提出了冻土蠕变计算的一种新方法,此法将分数阶微积分关系运用到了冻土蠕变计算中。
传统的流变模型是一种线性模型,黏滞系数被认为是不变的常数,不能很好地描述冻土蠕变的非线性特征,也不能反映冻土的加速蠕变阶段。本文基于传统的伯格斯模型,引入一种非线性黏滞体,其黏滞系数修正为时间和应力水平的函数,代替传统伯格斯模型中与弹簧并联的理想牛顿流体。在改进的伯格斯模型的基础上再串联一个由非定常、非牛顿黏壶和塑性体并联的黏塑性体,建立新的一维的非线性蠕变模型,如图1所示,进而推广到三维应力状态,通过与试验数据对比可知,该模型能较好地反应冻土蠕变的衰减、稳态和加速阶段。

图1 新的非线性蠕变模型
1 改进的非线性模型
1.1 引入非线性黏滞体
在传统的伯格斯模型中,土体材料的蠕变参数通常被认定为不变的常数,所以不能很好地反映蠕变的非线性特征。
根据冻土试验的等时应力-应变曲线,可以知道,冻土具有非线性蠕变特征,且其非线性过程与蠕变时间和应力水平有关。因此,本文引入一个非线性黏滞体,其黏滞系数η是时间和应力水平的函数,符合下面的公式
(1)
式中:m,n为材料的参数。
对式(1)进行求导,可得
(2)
上式说明η(t)是单调递增函数,当t从0→∞时,黏滞系数η(t)从0增加到η0,与文献[9]描述的蠕变规律较符合,由此得到非线性黏滞体的本构方程是:
(3)

1.2 建立改进的伯格斯模型
将引进的非线性黏滞体与弹性体及黏壶串联,得到改进的伯格斯模型,如图2所示。
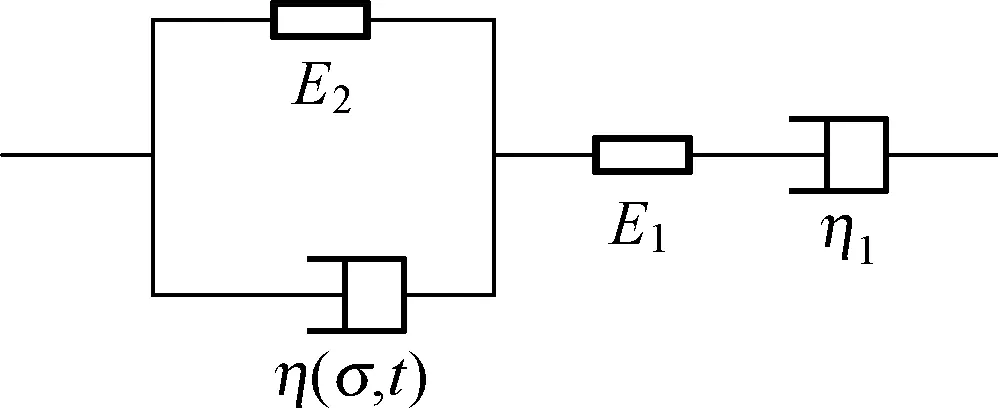
图2 改进的伯格斯模型
对于其中非线性开尔文体部分,根据非线性黏滞体的本构关系和串并联的应力、应变关系,可以得到它的本构关系为
(4)
式中:E2—弹性体的弹性模量;

由上式可以得到非线性开尔文体的应变蠕变方程为
(5)
由元件串并联的应力应变关系,可以得到改进的伯格斯模型的本构方程为:
(6)
建立三维流变模型很难用形象化的物理元件表示,所以不需要再通过对模型的组成元件的一一分析来建立三维模型,而可利用上面所得到的一维的结果,采用类比的方法,将一维的蠕变公式直接推广到三维的蠕变公式。模型中基本元件的一维和三维本构方程间的对应关系如下[10]
σ↔SijE1↔2G1E2↔2G2η1↔2H1η↔2H
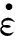
(7)
1.3 非线性黏塑性体
改进的伯格斯模型不能描述冻土在高应力作用下的加速蠕变,因此不妨引入一种非定常、非牛顿黏壶与塑性体并联的黏塑性体[5],如图3所示。
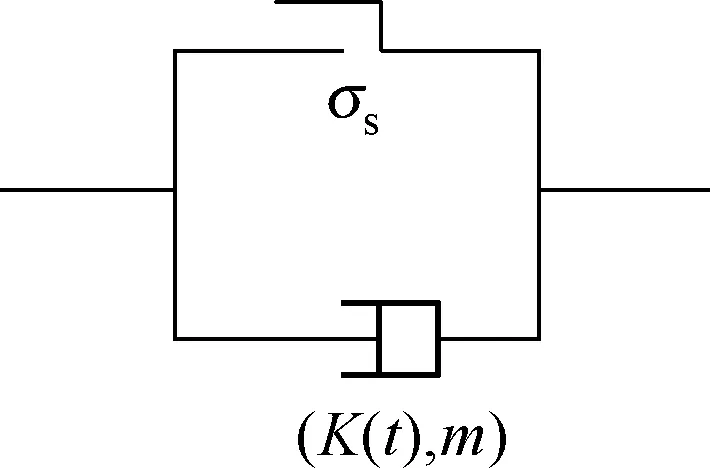
图3 非线性黏塑性体
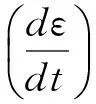
ε(t)=A(σ-σs)μtυ。



(8)
1.4 新的非线性蠕变模型
用改进的伯格斯体能描述冻土蠕变的衰减蠕变阶段和稳态蠕变阶段,再串联上非线性黏滞体即能描述冻土的加速蠕变阶段,便可以得到一个新的非线性蠕变模型,如图1所示。
综合以上推导,根据串并联的应力应变关系,可以得到该模型在单轴应力状态下的蠕变方程为
(9)
三维应力状态下的蠕变公式为
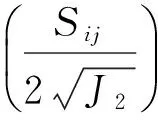
(10)
2 试验数据的拟合
2.1 稳态蠕变的拟合
本文采用曲线拟合的方法确定冻土蠕变非线性模型中的参数,数据采用尹晓文[8]等的冻土在不同温度下的三轴蠕变数据试验在4种不同温度(T=-5℃,-8℃,-11℃,-14℃)下进行,保持每个试件所受的平均应力偏张量第二法向应力σm不变,而应力偏张量Sij、不变量J2各不相同。试验数据及拟合曲线见图4,拟合参数见表1。
由拟合曲线和试验数据可以看出,冻土蠕变包括衰减蠕变和稳态蠕变两个阶段,模型很好地描述了冻土蠕变的这两个阶段。对于相同的应力偏量,温度越高,应变越大;对于相同的温度,应力偏量等幅度增加时,应变的增幅越来越大。
拟合曲线和试验数据的最大误差见表2,由表可知,对于不同温度同应力偏量水平而言,最大误差均差不过1%,说明新的非线性模型可以很好地描述冻土的稳态蠕变变形,拟合效果很好,且对于不同的温度均适用。

图4 各温度下冻土蠕变试验数据及拟合曲线

T/℃S11/MPaG1/MPaG2/MPanmH1/MPaH/MPa-51.25024.47914.4589.0622.152100.6473959.9891.50015.8389.7523.8866.39589.444896.9161.75012.9806.1765.4985.15995.1207051.0832.0009.6485.0044.7881.625103.0782925.157-81.25025.38811.2842.8883.425238.148102.5751.50012.94314.7673.9152.823121.4491027.0321.75013.77610.2394.7551.13192.2461427.1742.00010.9146.9553.2303.30798.375936.179-111.25036.85312.0625.9484.955238.3951083.0201.50018.00513.2303.1812.047120.104436.5321.75017.98411.0831.9972.00099.872153.6502.00011.4386.3102.3541.449132.800297.135-141.25043.86413.6814.6895.487731.538437.4921.50027.38412.9574.2803.421175.116701.3871.75015.72211.3983.1973.004143.3981128.8502.00012.6965.2633.6762.407299.5611535.533

表2 最大误差分析
2.2 加速蠕变的拟合
为了验证模型对加速蠕变阶段的适用情况,本文对李栋伟,汪仁和等[13]的试验数据进行了拟合,试验温度T=-15℃,轴压均为7MPa,围压分别为4MPa、5MPa、6MPa三种情况,试验数据和拟合结果见图5。

图5 -15℃冻土蠕变试验数据及拟合曲线
由图可知,模型对包括加速蠕变阶段的蠕变全过程均能较好地描述,最大误差不超过1%。当应力偏量较小时,试验只有衰减阶段和蠕变阶段,当应力偏量增加到一定值时,土体进入加速蠕变阶段而迅速发生破坏。加速阶段的拟合参数值为G1=4.496MPa、G2=16.648MPa、n=16.179、m=400.100、H1=8.831MPa、H=7.242MPa、A=51.439、k=1.622、υ=3.134和ν=1.114,这些参数能够反映此类冻土的加速蠕变特性。
3 结论
(1)本文对传统的伯格斯模型进行了改进,引入一种非线性黏滞体,代替传统伯格斯模型中与弹簧并联的理想的牛顿流体,再串联一个由一种非定常、非牛顿黏壶和塑性体并联的黏塑性体,建立了新的非线性流变模型,并将其推广到了三维应力状态,该模型可以描述冻土的衰减、稳定和加速蠕变阶段。
(2)根据冻土蠕变的试验数据,采用Origin软件,基于最小二乘法的原理,对试验数据进行了拟合。结果表明:1)该模型所拟合的曲线与试验数据吻合性较好,误差很小,而且适用于不同的温度。2)该蠕变模型不仅可以很好地描述冻土蠕变的前两个阶段,而且对于加速蠕变阶段也适用,这对于高应力下的冻土蠕变分析很有意义。
[1] 汪仁和,李栋伟,王秀喜. 改进的西原模型及其在ADINA程序中的实现[J]. 岩土力学,2006,27(11):1954-1958.
[2] 李栋伟. 高应力下冻土本构关系研究及工程应用[D]. 合肥:安徽理工大学,2005.
[3] 李栋伟,汪仁和,胡璞. 冻粘土蠕变损伤耦合本构关系研究[J]. 冰川冻土, 2007,03:446-449.
[4] 毛芬, 姚兆明. 人工冻土蠕变非定常开尔文模型[J]. 安徽理工大学学报:自然科学版, 2014,(2):13-16.
[5] 康永刚, 张秀娥. 一种改进的岩石蠕变本构模型[J]. 岩土力学, 2014,(4):1049-1055.
[6] 袁文华. 人工冻土黏弹塑性本构参数反分析研究[J]. 岩土力学, 2013,(11).
[7] 陈军浩, 姚兆明, 徐颖,等. 人工冻土蠕变特性粒子群分数阶导数模型[J]. 煤炭学报,2013,38(10): 1763-1768.
[8] 尹晓文, 傅强, 马昆林. 冻土三轴蠕变非线性数学模型研究[J]. 冰川冻土,2013,35(1):171-176.
[9] 王军保, 刘新荣, 郭建强,等. 盐岩蠕变特性及其非线性本构模型[J]. 煤炭学报,2014,39(3):445-451.
[10] 郑雨天.岩石力学的弹塑性理论基础[M]. 煤炭工业出版社出版,1988.
[11] 熊良宵, 杨林德. 硬脆岩的非线性粘弹塑性流变模型[J]. 同济大学学报:自然科学版, 2010,38(2):188-193.
[12] 孙钧.岩土材料流变及其工程应用[M].中国建筑工业出版社,1999.
[13] 李栋伟,汪仁和,赵颜辉,胡璞. 抛物线型屈服面人工冻土蠕变本构模型研究[J]. 岩土力学,2007,28(9):1943-1948.
