沉积粉尘二次飞扬现象的数值模拟研究

彭 驰，句海洋

(1．中煤集团山西华昱能源有限公司，山西 朔州 036900；2．中矿龙科能源科技(北京)股份有限公司，北京 101312)

在矿井巷道中，由于运煤过程、顶板掉渣以及沉降产生的漂浮粉尘，会导致巷道的底板沉积粉尘。当风速超过一定限度时，一部分沉积的粉尘会被重新扬起，形成漂浮粉尘，从而增加了风流中粉尘的浓度。粉尘浓度过高，不仅使井下工作环境恶劣，危害工作人员的身心健康，而且由于煤尘具有爆炸性，严重威胁着矿井的安全生产。因此，研究巷道内粉尘二次飞扬的规律，对治理粉尘、减少粉尘危害具有重要的意义[4]。

井下巷道内粉尘的二次飞扬受其粒径、湿度和风速等因素影响，通过现场实测法和实验室进行研究，均存在一定的困难。因此本文从数值模拟角度，运用GAMBIT进行三维建模并进行网格划分，采用FLUENT软件对不同风速下不同粒径粉尘二次飞扬过程及轨迹运用FLUENT模拟研究进行了探讨。研究尘粒在风流中的运动规律，可以在理论上定性、定量地搞清工作地点粉尘的运动特征及其在空间中的分布。

1 数学模型建立及其数值算法

离散相模型(DPM模型)属于欧拉—拉格朗日模型，即用欧拉方法描述气相流场，而用拉格朗日方法描述颗粒的运动。在本文计算中，连续相流场，即气相流场，使用湍流模型，采用SIMPLIC算法进行计算，颗粒的轨迹跟踪则由DPM模型完成。在这种条件下可以假设颗粒在流场中是稀释的，颗粒在连续相流场中运动，不仅受平均流场产生的阻力影响，还受到气流湍流脉动的影响。因为湍流流动是用湍流模型进行模拟的，只能在统计平均意义上表征湍流的宏观特征，而无法反映湍流流动的细节，所以用DPM模型计算出的单一颗粒轨迹没有实际意义，但是大量颗粒轨迹却可以在统计意义上反映颗粒在气相流场中的运动。湍流与颗粒之间的相互作用可以用随机轨道模型进行计算，也可以用粒子云模型进行计算。本文采用随机轨道模型模拟湍流影响作用。

1.1 气体的运动方程

巷道内空气流动符合气体连续方程：

(1)

气体运动方程：

惯性坐标系下，i方向的动量守恒方程为：

(2)

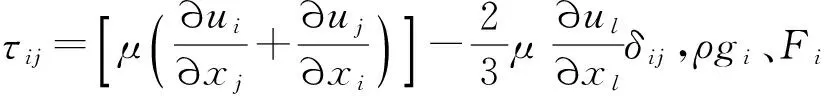
1.2 粉尘颗粒运动方程

1) 颗粒运动方程

FLUENT中通过积分拉格朗日坐标系下的颗粒作用力微分方程来求解离散相颗粒的轨道。颗粒水平方向的作用力平衡方程在笛卡尔坐标系下的形式为：

(3)

雷诺数

(4)

阻力系数

(5)

2) 湍流流动中的颗粒随机轨道

颗粒的湍流扩散模拟使用随机轨道模型，同时考虑到颗粒与连续相的耦合，确定给定时刻颗粒速度和位置：

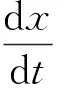
(6)

(7)

其中，1/α是颗粒弛豫时间。

对于单颗粒随机轨道在计算时，用流体的瞬时速度通过对单颗粒的颗粒轨道方程积分得到。为预测颗粒的弥散必须用到一个时间尺度T，它表示的是颗粒沿颗粒轨道ds做湍流运动的时间：

(8)

对于小颗粒，如果颗粒与流体之间的滑移速度为零，则积分时间则是流体Lagrangian积分时间TL，该时间近似为：

(9)

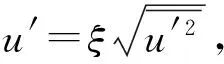
对于k-ε模型计算的流动，各点的湍动能是已知的，则各个速度分量脉动的均方根值，根据各向同性假设，为：

(10)

3) 颗粒尺寸分布

对于颗粒粒径分布，用Rosin-Rammler表达形式来确定颗粒的尺寸分布情况。对于尺寸分为足够多的组数，每组用其平均直径求解颗粒轨道。则直径大于D的颗粒质量分数为：

(11)

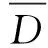
建立以上模型后，本文首先基于有限体积法、利用混合差分格式对偏微分方程组进行了离散化，然后利用混合差分格式和基于同位网格的 SIMPLC算法单相风流流动和气体—颗粒两相流动进行了数值解算。

2 物理模型及边界条件确定

2.1 物理模型建立

为了能真实、准确地模拟出煤矿井下巷道内流场的状况，依据综掘工作面的实际尺寸，应用 Fluent 自带的前处理软件 Gambit 建立了巷道的物理模型。巷道长100 m，宽4 m，高度为3 m，在底板上设置一组无初速度的粉尘粒子喷射源。因为重点模拟粉尘粒子的二次飞扬，风流在接近底板处由于粘性摩擦作用存在梯度问题，故对粉尘粒子沉落的底板进行边界层的划分，进行网格加密处理，以确保其结果的精确性。

连续相边界：本文给定了巷道的进口为速度口(velocity-inlet)边界条件，出口为出流(outflow)边界条件。

离散相边界条件：本文给定了巷道的壁面为“reflect”，边界条件并设定弹性恢复系数，出口设为“escape”边界条件。

2.2 边界条件和粉尘粒子参数设置

将用Gambit建成的物理模型导入到 Fluent 中，并对物理模型的边界条件和粉尘源参数进行了设置，见表1。

表1 边界条件和颗粒源主要参数

巷道内的风流速度由井下实际需要风量确定，根据《煤矿安全规程》规定，在巷道内风速限制在0.25～8.0 m/s范围内。所以本文选取了其中6个有代表性的风流速度作为考察对象，分别为0.25 m/s、0.5 m/s、1 m/s、2.0 m/s、4.0 m/s、6.0 m/s。其雷诺数与湍流强度分别由式(13)和(14)确定

(12)

式中：Re是雷诺数；ρ是空气的密度，1.2 g/m3；u是风流的速度，m/s；DH是巷道的水力直径；μ是风流的粘性系数，μ=1.808×10-5Pa·s。

湍流强度可以用下面的经验公式计算：

I=0.16Re(-1/8)

(13)

在各种风速条件下，风流的雷诺数与湍流强度的计算值见表2。

表2 不同风速下雷诺数于湍流强度

3 粉尘二次飞扬数值模拟结果分析

3.1 不同风速下粒子飞扬情况

下图为捕捉1 μm到100 μm之间不同粒径粒子，在长度为100 m巷道内运动轨迹，直至其被吹出巷道。

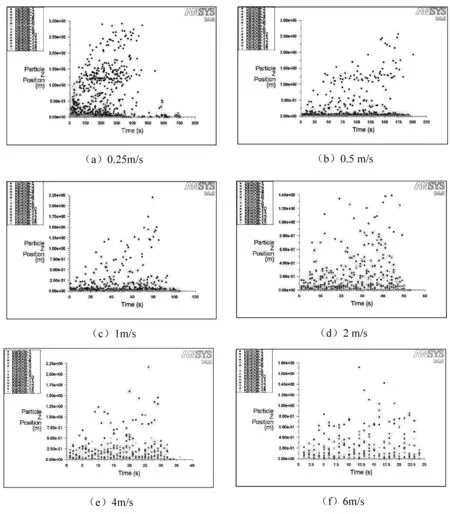
图1 不同风速下粒子二次飞扬轨迹

逐渐增加风速，观察颗粒物的移动状况。发现颗粒物明显滚动时，认为颗粒物已经起动，即二次飞扬。

由以上六张图可以看出，在不同风速条件下，不同粒径粒子引起二次飞扬，随风流方向运动100 m，飞扬高度不同。在风速小于0.5 m/s时，粒径在1 μm左右的粒子可以运动至巷道顶部；随着风流速度的加快，可以看到，在风速为1 m/s时，90%以上的粒子在巷道内飞扬高度不会超过两米；在风速到达4 m/s时，所有粒子在垂直方向上运动高度超过1 m之前已经被吹出巷道内，即二次飞扬粒子引起的危害不足以影响工作人员的健康。

3.2 不同粒径粒子二次扬起风速

尘粒在风流中的运动是垂直方向和水平方向运动的叠加。而在每一方向上依初速度的不同，可能经历加速或减速过程，然后以终极速度匀速运动。根据上述模拟结果得出粒子二次飞扬速度以及在垂直方向的运动高度，见表3。

表3 不同粒径粉尘粒子的二次扬起风速

4 结论

本文从数值模拟角度描述了煤矿井下粒子运动的数学模型，从理论层次分析了粒子的动力学运动特征。该模型从连续流场中考虑粒子的运动特征，并且分析了流速度和粒子之间的相对移动问题。

在风速小于0.5 m/s时，粒径在1 μm左右的粒子可以运动至巷道顶部；在风速为1 m/s时，90%以上的粒子在巷道内飞扬高度不会超过两米；在风速到达4 m/s时，所有粒子在垂直方向上运动高度超过1 m之前已经被吹出巷道内。另外，重点防止的是粒径为50～75 μm的粒子，在风速为2.3 m/s时，平均运动高度为1.4吗，即为呼吸带高度。

[1] 金龙哲，李晋平，等．矿井粉尘防治治理[M]．北京：科学出版社，2010．

[2] 程卫民，张清涛，刘中胜，等．综掘面粉尘场数值模拟及除尘系统研制与实践[J]．煤炭科学技术，2011，39(10)：39-44．

[3] 秦跃平，张苗苗，崔丽洁，等．综掘工作面粉尘运移的数值模拟及压风分流降尘方式研究[J]．北京科技大学学报，2011，33(7)：790-794．

[4] 徐景德，黄元平．沉积粉尘二次飞扬现象的实验研究[J]．煤炭安全．1996，1：8-9．

[5] 杨胜来．采煤工作面粉尘颗粒运动的动力学模型的探讨[J]．山西矿业学院学报，1994，13(3)：250-258．

[6] 于明州，金晗辉，陈丽华，等．粉尘粒子运动扩散特性的大涡模拟研究[J]．环境科学学报，2005，25(7)：891-895．