基于小波变换域的煤矿数字图件安全传输方法研究

石 强，陈 默，薛 阳，余桂希，余桂莲，余生晨

(1. 高河能源有限公司，山西 长治 047100；2. 北京政法职业学院，北京市 102600；3.宁夏中卫市海原县职业中学，宁夏 海原 755200；4. 宁夏固原市原州第五中学，宁夏 固原 756000；5. 华北科技学院，北京 东燕郊 101601)

0 引言

随着煤矿数字图件制作技术的日趋成熟和计算机网络的普及，数字化的煤矿信息能够以各种形式在网络上迅速便捷地传输和交流。煤矿数字图件(图像)比语言、文字蕴涵更大的信息量,因而成为煤矿在信息利用方面的重要手段。然而,由于制作煤矿数字媒体(数字地质图像、数字储量、钻井柱状图、数字音频、数字视频等)的完美拷贝非常的容易，从而可能会导致大规模的非受权拷贝，导致煤矿信息的泄露，给煤矿单位造成巨大损失。于是如何保护数字化的煤矿信息在网络上安全传输便显得日益重要。数据加密是目前常用的一种信息安全方法，但是被加密过的数字化煤矿信息是一堆乱码，容易引起网络攻击者的怀疑和破解的兴趣。如果把煤矿数字信息隐藏在一幅图像(风景图或不重要的煤矿图像)中，但又不明显的改变原图像的质量和视觉效果，这种改变很小，以致于在人类的视觉上，感觉不到这些改变。网络攻击者会认为嵌入有煤矿数字信息的载体图像只是一幅美丽的风景图或不重要的煤矿图像，从而达到不容易引起网络攻击者的怀疑和破解的兴趣，最后达到在网络上安全传输煤矿数字图件的目的。

信息隐藏(Information Hiding)是二十世纪九十年代中期从国外兴起的一门集多学科理论和技术于一身的新兴技术领域，它主要是利用人的感觉器官对数字信号的感觉冗余，以数字媒体或数字文件为掩蔽物，用空域掩藏和变化域掩藏等方式，将被藏信息掩藏于掩蔽信息(载体)之中[1-3]。对于信息隐藏技术，一般应满足如下要求：

不可见性(隐蔽性)：这是信息隐藏的基本要求。要求不影响对宿主信息(载体图像)的理解，即人的生理感官和计算机检测都无法发现宿主信息内包含了其他信息，同时不影响宿主信号的感觉效果和使用价值；

鲁棒性：要尽量保证隐藏了信息之后的宿主数据在经历可能的处理(如信号处理、有损压缩、滤波、调制等)、恶意攻击(如非法攻击、篡改、删除等)或者信道中随机噪声的影响后，还可以提取出原始的隐藏信息；

安全性：隐藏的信息内容应是安全的，应经过某种加密后再隐藏。同时隐藏的具体位置也应是安全的，要求至少不会因格式变换而遭到破坏；

对称性：通常，隐藏信息的隐藏和提取过程具有对称性，包括编码、加密方式等，以减少存取难度；

可纠错性：为了保证隐藏信息的完整性，使其在经过各种操作和变换后仍能很好地恢复，通常采取纠错编码方法；

效率：编码和解码的时空开销代价是否是可以接受的。

这里需要指出一点，对信息隐藏技术的不同应用，各有着进一步不同的具体要求，并非都需要同时满足上述要求。

其中不可见性与鲁棒性为煤矿数字信息隐藏的最基本要求,我们可以看出这两个特性是相互冲突的。不可见性(隐蔽性)要求嵌入的待隐藏的信息能量越低越好, 能量越低不可见性(隐蔽性)就越好，但是待隐藏的信息能量越低，越容易被破坏，不符合鲁棒性的要求，鲁棒性待隐藏的信息能量越高越好，能量越高，越不容易被破坏。那么，待隐藏的信息能量究竟是多少才合适呢？如何才能在不可见性与鲁棒性之间找到平衡呢？本文对这一问题给出了解决的方法。载体图像通过小波变换可分为低频、中频、高频部分。本文通过理论分析和实验发现待隐藏的信息嵌入到载体图像的中频部分，有可能在不可见性与鲁棒性之间找到平衡。利用基因算法确定待隐藏的信息的具体能量。实验证明该方法能够在不可见性与鲁棒性之间找到平衡，安全传输煤矿数字图件的效果较好。

1 基于小波变换域的数字信息隐藏算法

研究表明，由于人类视觉对于图像的各种成分具有不同的敏感性,为了提高信息隐藏的鲁棒性,应把待隐藏的信息加在载体图像的视觉重要部分,比如低频部分[4]。这一结果导致了变换域信息隐藏技术的发展，目前研究的信息隐藏绝大部分集中在变换域。在图像的信息隐藏算法中，有离散傅立叶变换、离散余弦变换、分形变换、小波变换等。近年来,基于小波变换域的信息隐藏算法已成为学术界研究热点之一。

小波域信息隐藏算法往往把待隐藏的信息嵌入到图像(载体)小波变换后的某些子带。从鲁棒性角度考虑，Cox等人[5]提出, 待隐藏的信息应放在视觉系统感觉上最重要的分量上。这个观点已被人们广泛接受。感觉上最重要的分量是图像信号的主要成分,携带较多的信号能量。图像经过小波分解后生成的小波图像,能量主要集中在低频部分,即低频部分是图像的主要部分,也是视觉重要部分。此外，图像的低频部分一般变化比较缓慢，抗干扰性强(即鲁棒性 也称稳健性好)。例如，一个低频成分持续2 cm，如果有人剪裁掉0.5 cm，那么，我们根据剩下的那1.5 cm图像还可较准确地恢复出整个2 cm的原图像。因此，从抗干扰性(鲁棒性)角度讲，应该选择将水印嵌入到小波图像低频系数(即低频成分)中[88]。但是，本文通过对人类的视觉特性进行理论分析和实验后发现，人眼对图像中平滑区域(低频部分)的变化一般比较敏感，在这一部分嵌入待隐藏的信息可能会引起原始图像质量下降，例如，嵌入待隐藏的信息容易引起图像模糊，所以，从不可见性角度讲，待隐藏的信息不应该嵌入这一区域。换句话说，把待隐藏的信息嵌入到小波变换后的载体图像的低频部分的算法符合鲁棒性的要求，但不符合不可见性(隐蔽性)的要求。

图像的高频部分是图像的细节部分。高频成分易受外来噪声、常规图像处理等因素影响，其稳定性较差。如果把待隐藏的信息嵌入到小波变换后的载体图像的高频部分的算法基本符合不可见性(隐蔽性)的要求，但不符合鲁棒性的要求。

综合考虑后，本文把待隐藏的信息嵌入到小波变换后的载体图像的中频部分，有可能在一定程度上，即满足不可见性的要求，又能满足鲁棒性的要求。实验证明了这个想法是正确的。

2 小波变换

小波变换理论是近年来兴起的新的数学分支，它是继1822年法国人傅立叶提出傅立叶变换之后又一里程碑式的发展，解决了很多傅立叶变换不能解决的困难问题。小波变换可以被看作是傅立叶变换的发展，即它是空间(时间)和频率的局部变换。

二维小波变换只是一维小波变换的重复使用。下面先看一看本文使用的一维小波变换。

小波变换把待分析的信号f(x)用基小波的ψ(x)伸缩尺寸和位移来处理，信号f(x)的连续小波变换定义为[6]：

对于数字信号f(n)进行二进小波变换，其数字滤波器表示形式为(Mallet算法)：

只要知道滤波器的系数hk和gk的值，就可计算出小波变换的结果。

利用公式Mallet算法就能把一维的图像信号分解成不同频段的信号，一维图像信号的高频部分(噪声部分)主要集中在了S=21和S=22尺度上，低频部分主要集中在了S=25尺度上[7]。

3 应用基因算法自动确定小波变换域数字信息隐藏最佳嵌入能量

不可见性与鲁棒性是信息隐藏的最基本要求。但是这两个特性是相互冲突的。对于一个特定的信息隐藏算法，必须折中考虑不可见性和鲁棒性，这实际上是一个如何确定信息隐藏的嵌入能量问题，对于前者，待隐藏的信息能量越低越好，而对于后者，待隐藏的信息能量越高越好。

以往的小波域信息隐藏算法没有很好地考虑嵌入信息的能量，只是根据实验结果来判断所选择的待隐藏的信息强度是否合适，如果选取的初始值不合适就必须重新选取初值对整个算法重新进行测试，其过程非常繁琐而且也很难找到使待隐藏的信息的不可见性与鲁棒性达到平衡的最佳值。本文采用的基因算法能比较好地解决这个问题。下面说明用基因算法确定最佳嵌入能量的方法。

1) 控制嵌入待隐藏的信息强度的α最佳值的确定

根据Weber定律，α理论上应小于0.01。也就是说，α的变化空间为0～0.01。在一个实际的待隐藏信息嵌入过程中究竟α取何值较为合适呢? 目前，通常的做法是通过人工多次取不同的α值来试验，这种实验过程费时并且往往达不到最佳效果。本文利用基因算法来比较自动地确定α的最佳值。

图像质量评价准则[8]。如前面提到的，待隐藏信息的鲁棒性与不可见性直接与嵌入的待隐藏信息强度有关，从而也影响到待隐藏信息图像(载体)的质量退化程度。如何评价由于待隐藏信息的嵌入而导致的原始图像退化的程度是一个着重考虑但实际上却常常被忽略的问题。在图像信息处理中大多数的退化程度或视觉质量评价均属差别失真评测准则。这些准则都是从原始图像与退化或失真图像的差图像得到的。在图像和视频编码及压缩中最常用的两个评测指标——峰值信噪比(PSNR：Peak Signal to Noise Ratio)和信噪比(SNR： Signal to Noise Ratio)，单位均为分贝(dB：decibels ) 。

设有两幅灰度图像为A=(aij)m×n和B=(bij)m×n，则它们的PSNR和SNR分别定义如下：

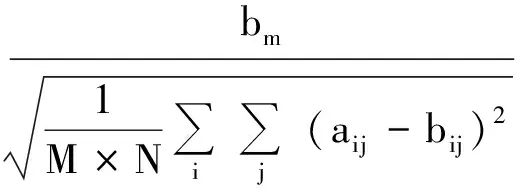
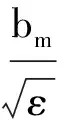
其中bm为图像像素所能取的最大值；其中，ε为均方误差，其定义如下：

ε越大说明嵌入待隐藏信息后的载体图像与原图像的差别也越大，ε越小说明两图像的差别也越小。虽然PSNR和SNR是比较成熟的和常用的衡量指标，但它们的计算较复杂。本文选ε作为因嵌入水印而导致的图像退化程度的评价准则，也既图像质量的评价准则(即评估函数)。

经理论分析和实验观察认为：一般来说，当均方误差ε<5%时，则认为嵌入待隐藏信息后的载体图像与原图像(载体)差别不大，符合不可见性的要求。

2) 基因算法

基因算法是人工智能的重要新分支，它来源于达尔文进化论：它根据适者生存，优胜劣汰等自然进化规则来进行搜索计算和问题求解。对许多用传统数学难以解决或明显失效的复杂问题，特别是优化问题，基因算法提供了一个行之有效的新途径，它对解决NP难题问题(非多项式算法问题)很有效果。

取前面叙述的图像质量评价准则—均方误差ε为基因算法的适应度函数ε。可按基因算法的步骤进行，即，选择(复制)、交叉、变异就可求得一个满足均方误差ε<5%的待嵌入的隐藏信息的强度。从而在煤矿数字图像的不可见性(隐藏性)与鲁棒性之间达到平衡。

4 实验结果与讨论

根据所提出的隐藏算法，本文编写了相应的计算机程序，进行了相关测试验证。

用小波变换(本文用Mallet变换)可把原图像(载体图像)进行五级分解。第一、二级为高频成分，第三为中频成分(嵌入水印)，第四为中低频成分(嵌入水印) ，第五级为低频成分[9]。

煤矿数字图像(信息)嵌入载体图像的计算过程步骤：

1) 选择待嵌入的煤矿数字图像，对其进行“之”字形扫描将其转化为一维数据即w={xi}，0

2) 对原始图像(载体图像)进行五级小波分解，得到不同分辨率级别下的细节子图；

3) 设原灰度图像(载体)为A=(aij)m×n；嵌入煤矿数字图像后的载体图像为B=(bij)m×n，其中，aij、bij分别表示原始图像像素(或从原始图像中提取的特征)和嵌入煤矿数字图像的图像像素(或改变后的图像特征)。

按如下的公式将煤矿数字图像序列嵌入到第三级中频成分和第四级中低频成分的小波系数中[10]，

bij=aij(1+α×xi)

对灰度图像而言，bij的一半嵌入到第三级中频成分的小波系数中；而另一半嵌入到第四级中低频成分的小波系数中。上式中，xi为煤矿数字图像信号分量，即w={xi}，0

4) 对修改后的小波系数进行小波反变换，便得到含有煤矿数字图像信息的混合图像。

图1中，(a)为载体图像——矿床图像，(b)为待嵌入的隐藏图像——巷道与陷落柱图像。(c)为嵌入巷道与陷落柱图像后所得的图像, 即混合图像，(d)为提取出的巷道与陷落柱图像。

图2中，(a)为载体图像——海湾像，(b)为待嵌入的隐藏图像——陷落柱图像。(c)为嵌入陷落柱图像后所得的图像, 即混合图像，(d)为提取出的陷落柱图像。

实验结果表明，利用本文提出的嵌入算法具有很好的不可见性，提取的图像几乎与原始图像一样，从而证明本文提出的算法可以在煤矿数字图像的隐藏性(不易被察觉，或不可见性)与鲁棒性(当被保护的信息经过某种改动后，不容易被破坏)之间达到了平衡。同时也证明了该方法(算法)安全的传输煤矿数字图件的效果较好。

图1 巷道与陷落柱图的嵌入及提取

图2 陷落柱图的嵌入及提取

[1] 钱思进. 信息隐藏与信息安全[C]. 北京：第二届全国信息隐藏学术研讨会论文集[A].2000,6：136-138.

[2] 丁玮. 数字图像信息安全的算法研究[D].中国科学院计算技术研究所，2000.

[3] 郭 磊,郭宝龙.小波域数字图像水印算法的研究[J].计算机工程与应用,2008,13(2):6-8.

[4] 陈武凡.小波分析及其在图像处理中的应用[M].北京:科学出版社,2010:75-76.

[5] Cox,J. Secure spread spectrum watermarking for multimedia[J].IEEE Transactions on Image Proceedings. 2013,6(12):1673-1687.

[6] Ramchandran K. and Vetterli M. Best wavelet packet bases in a rate-distortion sence[J]. IEEE Trans. IP. 2010，(2)：160-175.

[7] Coifman R. R. and Wickerhauser M. V. Adapted waveform analysis as a tool for modeling，feature extraction and denosing[J]. Optical Engineering，2013，33(7)：2170-2174.

[8] Goodman T. N. T.，Lee S. L. and Tang W. S. Wavelet wandering subspaces[J]. Trans. Amer. Math. Soc，2011，338(2)：639-654.

[9] Donovan G.，Geronimo J. S.，Hardin D. and Massopust P. Construction of orthogonal wavelets using fractal interpolation function[J]. SIAM J. Math. Anal.，2014，27：1158-1192.

[10] Walter G. G. A sampling theorem for wavelet subspace[J]. IEEE Trans. Inform. Theory，2013，38(2)： 881-884.