岩石性质对爆破振动传播规律的影响

徐振洋，郭 浩，郭连军，刘 鑫

(1.辽宁科技大学 矿业工程学院，辽宁 鞍山 114051；2. 辽宁冶金地质勘查局 四0三队，辽宁 鞍山 114051)

0 引言

爆破振动受多种因素影响，主要包括岩体的力学性质、药量、微差时间、孔径、自由面等[1]。在这些因素中，爆破地质条件往往占主要作用，因此结合岩石的力学性质试验来区别不同岩性的变化对振动影响具有关键作用。岩体的破坏过程主要包括弹性变形阶段的弹性势能，塑性变形中的塑性势能，破坏时的动能以及其它形式能[2]。研究人员常以应力—应变的变化来阐述岩石在变形破坏过程力学特性[3]。在台阶爆破中，炸药的爆炸能转换为地震波的能量与岩石的弹性势能有直接关系[4]。

鞍钢大孤山铁矿是鞍钢主要矿石生产地之一，现采用露天台阶逐孔起爆技术进行爆破，同时与鞍钢炸药厂自身研制的高性能乳化油炸药配合使用。随着开采范围的改变，采场的开采深度不断增加，矿岩种类和特性都会产生较大的变化，岩石性质对爆破效果影响较大[5,6]，对岩石性质与爆破振动传播规律进行研究，有利于深入研究炸药爆破能量在爆破中的利用情况。

1 岩石力学参数测试

对爆区岩样进行岩石力学试验，测得指标包括岩石密度、普氏系数、抗压强度、抗拉强度、弹性模量、泊松比、内聚力、摩擦角等。三种典型的岩样的物理力学性质试验如图1，所测定结果汇总表如表1。

图1 岩石力学性质试验

岩石名称轴向与层理块体密度/g·cm-3抗压强度/MPa抗拉强度/MPa抗剪参数变形参数内聚力/MPa摩擦角/°弹性模量/GPa泊松比混合岩平行垂直平均2653789285673426442530396840710900400066320205315497578654132544250295千山花岗岩平行垂直平均2575493535170640824244019814751215204184412802668252351613413341860225磁铁石英岩平行垂直平均36312057894159042039762022983715602569404379080241094712272079541238835023

2 爆破振动测试

2.1 监测依据

大孤山铁矿爆区的爆破设计采用的是逐孔起爆技术，地表使用是由澳瑞凯公司生产的段别为17 ms，25 ms，42 ms高精度高强度导爆管雷管，孔内延期为400 ms，炸药类型为乳化油炸药，布孔方式为方形布孔,孔距6.5 m，孔深15 m，炮孔孔径为250 mm，台阶高度为13 m。选取单孔最大装药量为近乎相同，爆区设计相近的爆破设计方案进行振动数据监测。测振采取的形式主要采用固定测点，测振仪器的摆放沿着上个台阶的边帮方向，这样可以对比在相似爆破设计参数中三种不同岩性的测振点的振动衰减特征：一方面有利于在同一岩种不同距离处形成鲜明的对比，另一方面也有助于形成不同岩种之间的衰减规律的对比[7]。

2.2 爆破振动监测

监测点的布置应在距爆源中心30 m，60 m，90 m的同一直线上，并分别放置爆破振动测试仪一台，对测振仪器进行编号，监测示意图如图2。其中1#、2#、3#为磁铁石英岩爆区的监测布置点，4#、5#、6#为花岗岩的爆区监测点，7#、8#、9#为混合岩的布置监测点。爆破振动监测数据见表2。

图2 爆破振动监测示意图

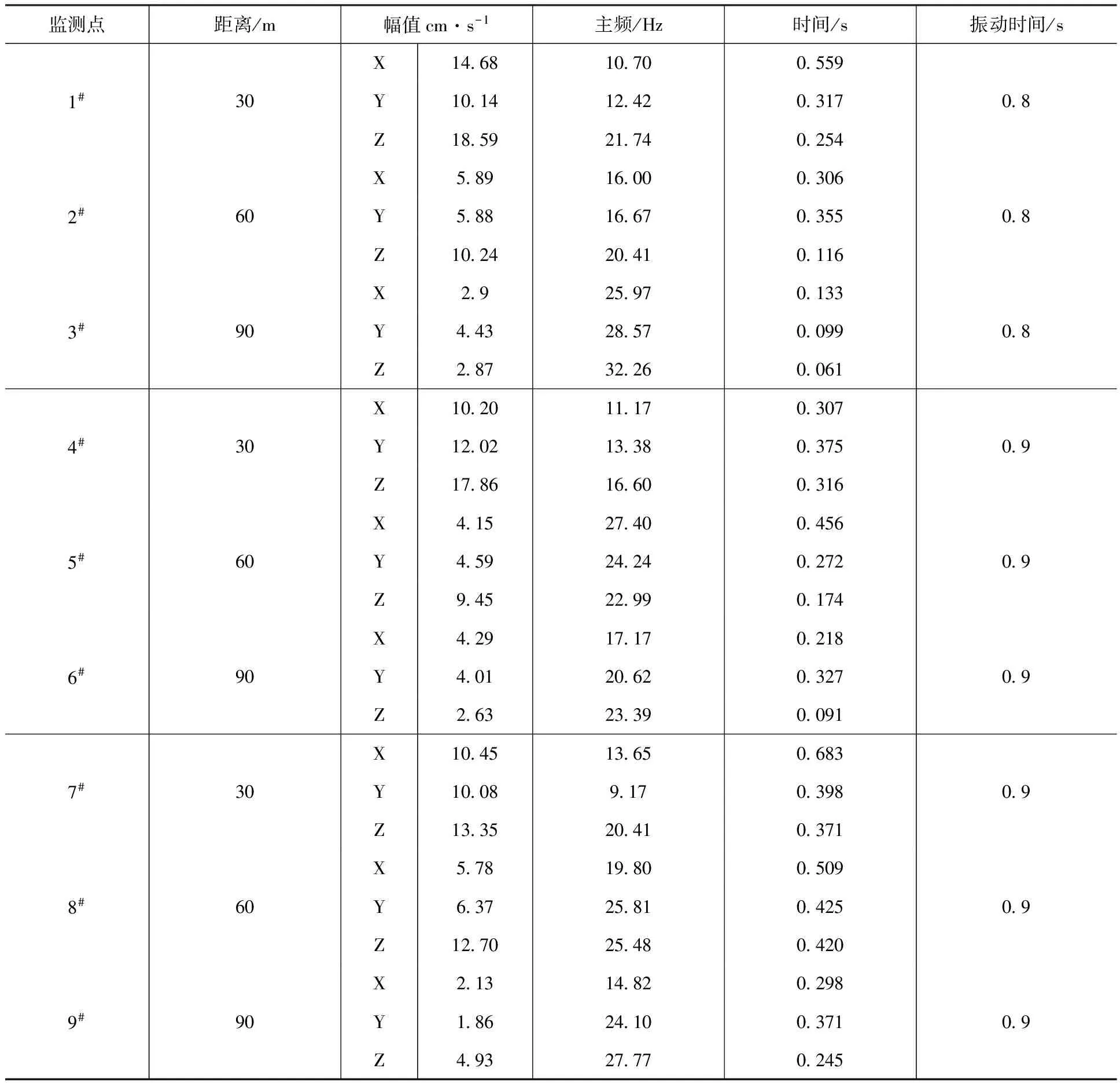
监测点距离/m幅值cm·s-1主频/Hz时间/s振动时间/s1#30X146810700559Y101412420317Z185921740254082#60X58916000306Y58816670355Z102420410116083#90X2925970133Y44328570099Z28732260061084#30X102011170307Y120213380375Z178616600316095#60X41527400456Y45924240272Z94522990174096#90X42917170218Y40120620327Z26323390091097#30X104513650683Y10089170398Z133520410371098#60X57819800509Y63725810425Z127025480420099#90X21314820298Y18624100371Z4932777024509

3 爆破振动信号分析

3.1 爆破振动速度分析

在研究爆破地震波的能量强度指标时，通常选取的是振动速度曲线之间的峰值区段[9]。对爆破振动的相关的量纲物理量进行统计分析，进而来反映岩体能量利用率的变化情况[10,11]。爆破地震波的峰值变化情况如图3～5。

图3 混合岩振动峰值速度衰减

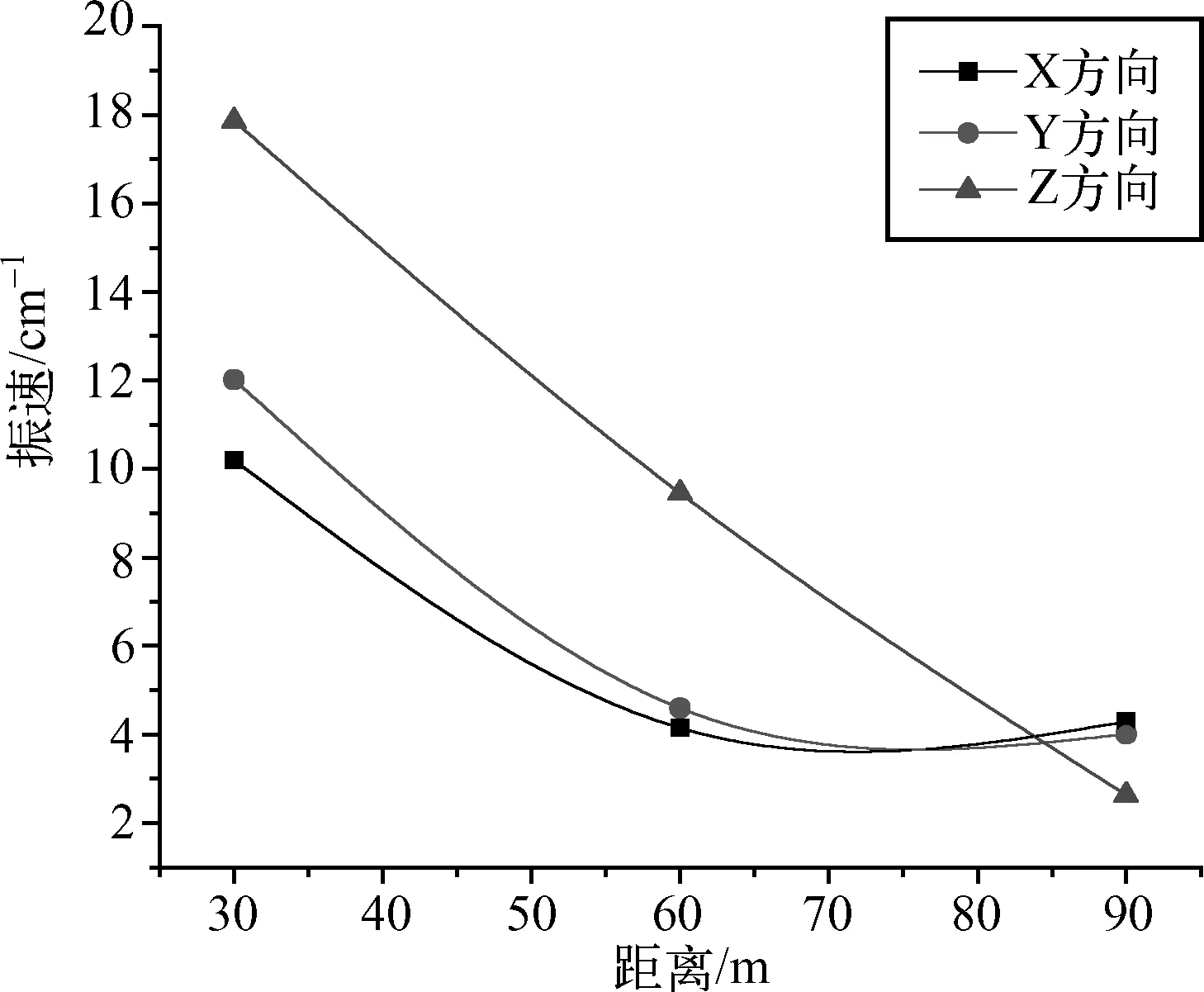
图4 千山花岗岩振动峰值速度衰减

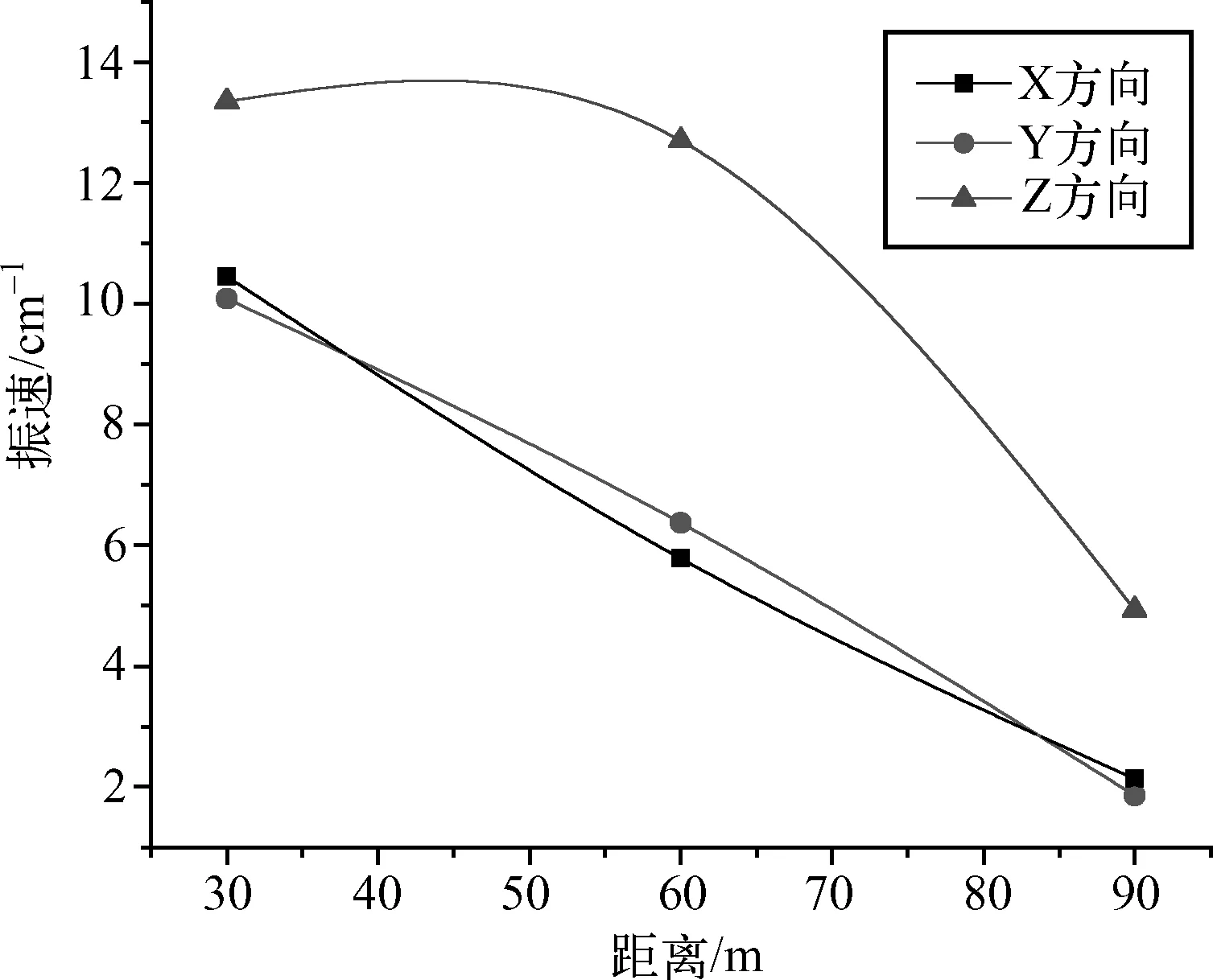
图5 磁铁石英岩振动峰值速度衰减

由图3～5可以明显的区别出三种岩石的衰减趋势，三种岩石爆区的速度振动峰值在不同监测点处X、Y、Z方向的具有不同的峰值，总体表现为Z方向峰值最大，但随着距离的增加Z方向的峰值有可能达到最小。

从三爆区中的总衰减趋势可以看出，图3和图4的总衰减趋势成凹状，且图3的凹陷度较大，表明衰减较大，而图4成凸状，表明衰减程度较小。

对三种岩种振动数据的Z方向的数据进行衰减规律回归分析，磁铁石英岩区爆破的相关系数为0.94，K、α分别为171、1.57。花岗岩区爆破的相关系数为0.94，K、α分别为185、16。混合岩区爆破的相关系数为0.85，K、α分别为46.5、0.82。对比三种岩石的炸药量与振动速度的关系，基本上符合工程上对相关系数的要求(一般为r=0.85)，三种岩石的爆破衰减系数不同，同种药量的情况下，不同岩种的衰减系数不同。

3.2 能量利用分析

露天爆破过程中，炸药能的有效利用一直未被直接测量，一般都是通过间接测量的手段来评价炸药的利用情况。炸药在岩石中爆炸产生的能量，主要用于岩石的破碎、地震波传播和岩石的抛掷，可以用下式表示[12]：

EE=EF+ES+EK+ENM

(1)

式中，EE为爆炸能，EF为破碎能，ES为波能，EK为动能，ENM为损失能，各种能量以各自与总爆炸能量的比例形式表示，其中(1)中前三项为炸药爆炸能量主要消耗部分。

爆破地震能量是以能量流通过指定的距离的可控面得出的，则研究重点为ES。能量通量是表面应力和质点速度的矢量积，表示为[13]：

Φ=τijnivj

(2)

为了和速度联系起来，地震仪的读数，应力值以及一些假定必须提前给出。如果地震波被看成是在无穷的均匀的介质中的纵向的球面波，在球坐标中应力张量的主要成分：

(3)

式中，r—爆源中心的距离，u1为质点位移的径向分量，λ和μ为拉梅常数。

对于球面波的波峰，它的标准的主轴单位向量是(1,0,0)单位向量，将(3)代入(2)得到通量公式：

(4)

假设通过半径为r的球面的总能量为定值，则通量为：

P=4πr2Φ

(5)

则地震波能公式为：

(6)

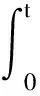
(7)

位移的空间倒数可以近似有以下关系：

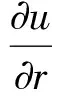
(8)

式(8)中c是波速，其在v≤c时适用。所以，地震波能量的计算公式为：

(9)

(10)

在实际计算中取(10)式的绝对值，有：

(11)

上式求得的地震能量，是一个球面波或平面P波在弹性介质中拥有的质点速度的径向分量v1，纵向的分量需要实地测量。假设速度的横向和垂直分量(v2和v3)属于横波速度，利用平面波近似理论，得到下列关系式：

(12)

(13)

为了进一步得到能量的通式，通常被进一步简化，得到：

(14)

(15)

式中，v为振动速度；K、α为场地系数；Q为最大单响药量；r为测点到爆区的距离；r0为空腔半径。

为进一步阐述能量的转化率问题，通过运用炸药能为转换为爆破地震波能量百分比的概念，来分析爆源因素对爆破地震波强度的影响。定义η为炸药能量转化为地震波初始能的百分比，则：

(16)

从地震波能量公式可知：在地震波能与炸药量、岩石性质、距爆源的距离等参数有关。速度的大小在一定程度上反映了能量的大小，而地震波能量在一定程度上反映了炸药能量的损耗，在同一输入能量的情况下，只要确定了地震波的能量，就能确定炸药的利用率。而地震波波速常采用振动监测仪对其进行监测。

为了进一步分析三种岩石的地震波能量转化情况，通过对比能量的公式可以发现在药量、孔径、距离相同的情况下，地震波的能量只与ρ、K2、α值有关，而由能量的峰值能量公式可知，α值相差不大，可以近似相等，则地震波能量与ρK2正相关，而ρ值在力学性质试验中已经得到。

针对不同岩性的三种岩石的地震波能量转化情况进行对比分析：磁铁石英岩和千山花岗岩的最大一响装药量相同，则两种岩石爆区炸药能转化为地震波能量就只与ρK2相关，则：

(17)

m<1，说明千山花岗岩转化为地震波的能量较多，炸药的能量利用率相对较低。

混合岩的爆区的最大单响药量为450 kg，药量的改变也会造成炸药能量转化的改变，因此通过对比磁铁石英岩和混合岩的能量转化，有：

(18)

对比η磁和η花和η混的大小关系：η混<η磁<η花，在不考虑其它能量损失的情况下，该值的大小表明能量的损失程度，数值越大表明损失越大，也即表明能量的利用率低。炸药在混合岩中的能量利用率最高，花岗岩和磁铁石英岩次之。不同岩石对炸药能量的利用程度不同，主要是因为不同的岩石具有不同的力学性质。由磁铁石英岩和千山花岗岩具有较高的抗压、抗拉强度和弹性模量。在较高的岩石应变率条件下，保持较高的韧性，破碎时需要较大的能量，并表现为不容易破坏，当炸药释放的爆炸能达不到岩体破碎强度时，则表现为转化地震波的能量较高。而两者的差别主要在于岩体结构的方向的不同，混合岩自身结构的节理裂隙发育较差，导致其片麻岩相对抗拉、压强度较低，易于破碎，在输入能量相同的条件爆破后，能量的利用程度较高，相对容易爆破。

地震研究中，地震波能量转换关系与萨道夫斯基中的场地系数K和α有关，并给出了理论换算公式[15]：

η=(K×10-2-α)3/α

(19)

该理论公式的提出有助于定量的表示炸药爆炸能转化为地震波的百分比，通过对地震波能量的回归分析获得的结果可以定量的得到不同岩石爆区的地震波能量转化率。在相同炸药量的转化情况下，为η千>η磁。在不同药量情况下，主要考虑的是单位药量的转化系数，为η磁>η混。表明爆破介质对地震波能量的转化起作用，磁铁石英岩和花岗岩爆区的地震波能量转化率较高，混合岩爆区的地震波能量转化较低。

4 结论

1) 在30 m监测处的振动数据表明垂直方向的速度峰值大于其它两个方向，而衰减规律总体表现为Z方向振动峰值衰减较为迅速。

2) 爆破振动衰减与岩石性质有较大关系，磁铁石英岩和花岗岩具有较高的弹性势能，故由监测速度计算得到的地震波能量较高，混合岩的地震波能量较小。

3) 在相同的炸药量情况下，炸药的能量利用与爆区的岩石力学性质有关，地震波能量有随ρK2增大而转化率增大的趋势。

4) 不同爆区的岩石衰减表现出不同的趋势，表现出衰减曲线的凸凹程度的不同，总体上呈近区衰减快的趋势，主要是与岩体的结构有直接关系。

[1] 林大超，白春华.爆炸地震效应[M].北京：地质出版社，2007.

[2] 谢和平，陈忠辉.岩石力学[M].北京：科学出版社，2004.

[3] 赵忠虎，谢和平.岩石变形破坏过程中的能量传递和耗散研究[J].四川大学学报(工程科学版)，2008，40(2)：26-31.

[4] 尤明庆，华安增.岩石试样破坏过程的能量分析[J].岩石力学与工程学报，2002，21(6)：778-781.

[5] Wang, Q. Z., Li, W., & Xie, H. P. Dynamic split tensile test of flattened Brazilian disc of rock with SHPB setup [J]. Mechanics of Materials, 2009, 41 (3): 252-260.

[6] Wang, Q. Z., Li, W., & Song, X. L. A method for testing dynamic tensile strength and elastic modulus of rock materials using SHPB[J]. Pure and Applied Geophysics, 2006, 163 (5-6): 1091-1100.

[7] 张义平，吴贵义.爆破震动波特性研究[J].矿业研究与开发，2007，12：27-6.

[8] M. A.萨道夫斯基，陈英方译.地震预报[M].北京：地震出版社，1986.

[9] 许红涛，卢文波.几种爆破震动安全判据[J].爆破，2002，19(l)：8-10.

[10] 卢文波，赖世骧，舒大强，等.关于爆破振动速度和加速度效性问题的讨论[J].爆破，2000，17(S1)：11-14.

[11] 李彬峰.爆破地震效应及其控制措施分析[J].爆破，2003，20(2)：83-85.

[12] Spathis A. T. On the energy efficiency of blasting[C]. In: Proceedings of the sixth international symposium on rock fragmentation by blasting, Johannesburg, 8-12 August. Johannesburg: The South African Institute of Mining and Metallurgy, 1999, 81-90.

[13] Achenbach J. D. Wave propagation in elastic solids[M]. Amsterdam， Elsevier, 1975：166.

[14] 郭学彬，肖正学，张继春，刘泉.论爆破地震波在传播过程中的衰减特性[J].中国矿业，2006，15(3)：51-57.

[15] 张少泉，郭建明.爆炸地震的能量转换系数计算及其应用[J].地球物理学报，1984，27(6)：537-548.