基于BIQI的JPEG2000压缩失真图像质量评价算法研究

罗晓梅，邹 海

（安徽大学 计算机科学与技术学院，安徽 合肥 230601）

1 引言

图像质量评价包括主观图像质量评价和客观图像质量评价，因人眼视觉系统（Human Visual System,HVS)是图像处理的终端，因此主观图像质量能够得到最为准确的质量评价结果.但是主观图像质量评价操作繁琐，费时费力，无法实时处理[1].而客观图像质量评价是通过数学模型计算失真图像和原始图像的失真度，客观图像质量评价方法可分为三类：全参考，部分参考和无参考.例如峰值性噪比（Peak Signal to Noise Ratio,PSNR)[2]和均方误差(Mean Square Error,MSE)是最简单的全参考图像质量评价算法，以及Wang等人提出的结构相似度理论(Structure Similarity,SSIM)[3]，由于该类算法具有计算复杂度低，物理意义清晰等优点，MSE和PSNR,SSIM多年来应用最广泛.全参考图像质量评价所产生的算法和人类视觉感知相关性良好，然而在很多场合，原始图像无法获取时，这时只能采用无参考图像质量评价方法.

传统的无参考图像质量评价都是基于失真测量的思想，即假设失真类型及其特点已知，通过测量失真的强度得到图像质量.这类方法过于强调失真而忽视图像本身的属性，质量评价性能往往不高，而且只适用于特定失真类型的图像.如：JPEG[4],JPEG2000压缩失真图像[5,6]和高斯模糊图像[7].为了寻找在不知道特定失真类型的情况下更为有效的无参考图像质量评价算法，许多学者研究了以下方法：（1）基于训练学习的方法，这类方法首先提取图像的感知特征，例如基于支持向量机学习的方法[8],这类方法的缺点在于它依赖于有效的特征提取算法，且需要主观得分来训练学习.（2）基于自然场景统计模型的方法，该方法即假设自然图像或失真图像都只是所有图像信息的一个微小子集，试图通过寻找两者之间的差异来评价图像质量，例如楼斌,沈海斌等人提出的基于NSS（Natural Scene Statistics,NSS）与HVS的小波域线性预测方法[9].

Moorthy等人提出的先从图像的小波域提取统计特征，并利用分类算法求出失真概率判断失真类型，再根据质量评价算法，把所有失真类型的概率和各自失真质量结合起来，最后加权求和的BIQI(Blind Image Quality Index,BIQI)[10]失真图像质量评价算法.BIQI算法计算各类失真图像概率及质量分数分模块进行，本文针对BIQI算法在评价JPEG2000压缩失真图像质量时与人类主观得分差距较大的问题，提出基于BIQI的JPEG2000压缩失真图像质量评价算法.

2 BIQI算法及相关分析

2.1 BIQI两步框架

BIQI算法是一个基于两步框架，模块化的无参考图像质量评价算法.该两步框架为：图像失真分类（JPEG2000,JPEG,WN,GBlur,FF)；评估失真图像的质量.算法中pi{i=1,2,3,4,5}表示每个失真图像所属五类失真的概率，qi{i=1,2,3,4,5}表示失真图像所属分类的质量分数.失真图像的最终质量采用概率加权求和表示：

2.2 失真图像统计

BIQI算法首先在3个尺度3个方向上使用双正交9/7小波变换，获得子带因子，这些子带因子使用广义高斯分布（generalized Gaussian distribution,GGD)模型进行参数化.广义高斯分布(GGD)为：

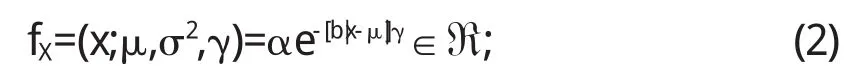
其中，μ,σ2,γ分别表示失真的均值、方差和形状参数.其中：

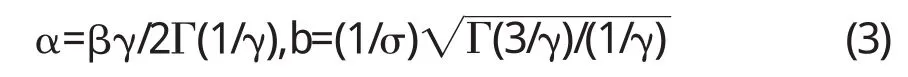
Γ(·)表示 gamma函数

其中分布的参数（μ,σ2,γ）使用文献[11]提出的方法进行评估.获得的参数σ2,γ在3个尺度，3个方向上组成一个18维的向量軆fi，表示图像的特征向量.给定失真图像的训练和测试集，使用带有径向基函数（radial-basis,RBF)的支持向量机v-SVM联同特征向量軆fi将失真图像分类为5个失真类型，即JPEG2000,JPEG,WN,Blur,FF.需要注意的是，分类到特定失真类型并不表示这些失真类型不相交，事实上，这些失真类型在某种程度上是相交的，即一副失真图像的分类是通过SVM[12]评估图像的失真概率所确定的，值越大表示该图像所属的失真类型概率越大.

2.3 算法分析

选用LIVE图像质量评价数据库[13]中的图像进行试验，描述BIQI算法的性能.该数据库中包含29副无失真的参考图像和五类失真图像(JPEG2000,JPEG,BLUR,WN,FF).该算法对于JPEG,高斯白噪声，模糊失真具有良好的评价效果，且失真分类准确率达到80%以上，并且与全参考图像质量评价算法PSNR有着很强的竞争力.但是对于JPEG2000，FF图像失真类型与人类视觉感知相关性不是很理想.由于BIQI算法评价JPEG2000压缩失真图像质量分数与主观得分DMOS差距较大，文献[6]对于单独评价JPEG2000压缩失真图像质量有着良好的评价效果，据此，针对JPEG2000压缩失真图像，提出基于BIQI的JPEG2000压缩失真图像质量评价算法.

3 基于BIQI的JPEG2000压缩失真图像质量评价算法

采用文献[6]的方法评价JPEG2000压缩失真图像质量，并将该方法计算出的失真图像质量分数与BIQI算法相结合，采用概率加权求和的方式得到最终的JPEG2000压缩失真图像质量.

3.1 自然场景统计

使用文献 [14]提出的自然场景统计模型构造JPEG2000压缩和未压缩失真图像的简化模型.该方法通过量化自然图像和失真图像的偏离程度预测失真图像的质量.该方法的成功表明了人类对图像的感知与图像失真的感知、图像的自然性相关.

3.2 JPEG2000压缩失真图像质量

首先使用离散小波变换(discretewavelettransform,DWT)和基于小波图像压缩所导致的JPEG 2000压缩标准[15]对JPEG2000失真图像进行压缩.再使用文献[16],[17]中提出的统计模型：

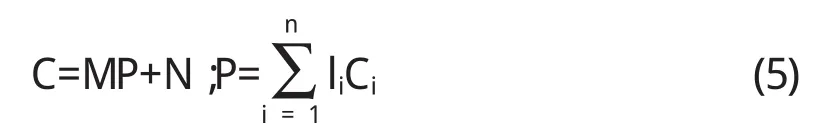
其中C代表小波系数的幅度，P代表系数的线性预测的调节幅度，M,N是被假设为独立的零均值随机变量，系数Ci表示C在空间，尺度和方向的n个系数邻域，li表示线性预测系数.

使用简化的二态小波域自然场景统计模型，获得 4个经验概率，Pii,Pis，Psi，Pss，其中 Pss对于视觉质量损失提供了最佳的适应值，可以最小化质量预测误差.因此从6个子带（水平，垂直，第二最佳分辨率的对角线方向，水平，垂直，最佳分辨率的对角线方向）计算Pss的特征值，提出非线性变换每个独立子带特征.其中，特征转换算法为：

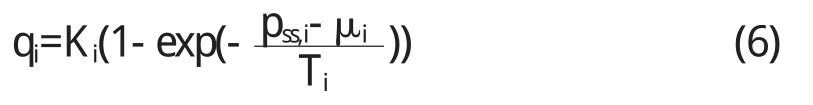
其中qi表示第i个子带的变换特征（预测图像的质量），pss,i表示第 i个子带的 pss概率，Ki，Ti，μi表示第i个子带的曲线拟合参数.每个子带特征被映射为主观质量.变换特征的加权平均被用来预测图像的质量.由于水平和垂直子带在特定尺度的相似性，将给定规模相同方向的权重规定为相同.因此，将六维子带质量向量调整为四维向量，在给定规模的水平和垂直子带预测其平均质量.最终预测的质量采用加权平均质量a'表示，即：

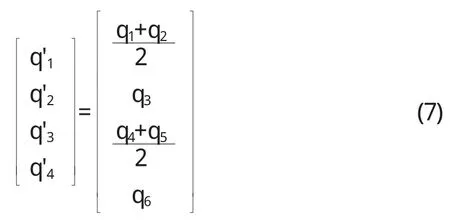
由此得到JPEG2000压缩失真图像质量为

运用以上算法计算出JPEG2000压缩失真图像质量分数后，由BIQI算法得到该失真图像的最终质量.即q1=Q,

4 实验结果与分析

为了验证本文提出的无参考图像质量评价算法，使用LIVE图像质量评价数据库[13]进行测试，该库有29副原始参考图像与经过5类失真处理后的图像，其中JPEG2000压缩失真图像227（1-227）副.图1表示经过JPEG2000压缩后的失真图像.图2表示该图像所属五类失真（JPEG2000，JPEK,WN,GBLUR,FF)的概率.从图2五类失真所占概率大小可以看出该副图像属于JPEG2000压缩失真.

图1 JP2K失真图像

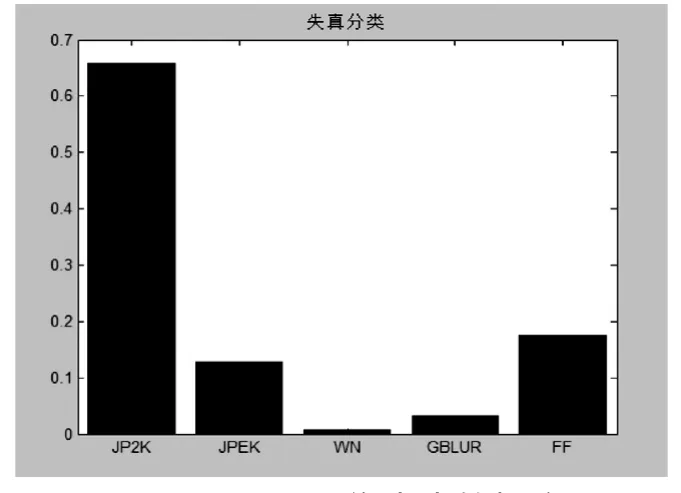
图2 JP2K图像失真的概率

将文献[10]原BIQI算法和PSNR算法得到的图像质量与图像的主观得分DMOS做对比得到其绝对预测误差直方图如图3所示.

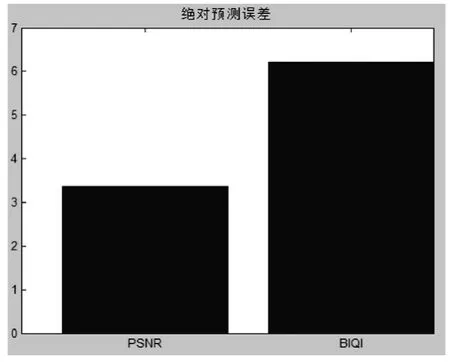
图3 BIQI，PSNR与DMOS绝对预测误差直方图

图3显示，BIQI算法预测该JP2K压缩失真图像质量与主观得分DMOS之间的差距较PSNR与DMOS之间的差距要大.

采用本文改进后的算法，得到的质量评价结果与DMOS对比，如图4所示.

图4 改进后的BIQI,PSNR与DMOS绝对预测误差

图4显示，改进后的BIQI算法评价质量与主观得分DMOS之间的差距较PSNR与DMOS之间的差距要小，与人类主观感知相关性良好.

从LIVE图像质量评价数据库[13]中的JPEG2000压缩失真图像中选取5副失真程度不同的图像，分别采用PSNR，文献[10]和本文的算法进行质量评价并将DMOS作为客观评价的标准.其结果如表1所示.

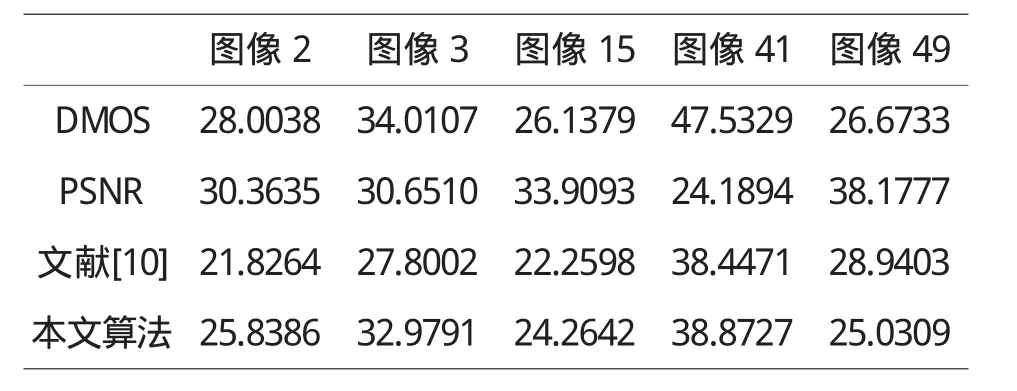
表1 不同算法对JPEG2000失真图像质量的评价

从表1中可以看出，本文算法计算出的JPEG2000压缩失真图像质量与文献[10]相比，更接近主观得分，且优于PSNR评价算法.但该算法在评价少数JPEG2000压缩失真图像时，存在质量略低于文献[10]和PSNR的现象，有待于进一步改进.

5 结论

本文针对BIQI算法在评价JPEG2000压缩失真图像质量时与人类主观得分差距较大的问题，采用文献[6]中算法对JPEG2000压缩失真图像质量进行预测，并将该算法计算出的失真图像质量分数与BIQI算法相结合，采用概率加权求和的方式得到最终的JPEG2000压缩失真图像质量.实验结果表明，改进后的算法与人类主观得分差距要小，与人类主观感知相关性良好.

〔1〕Viola P,Jones M,Snow D.Detecting pedestrians using paterns of motion and appearance[J].Computer Vision,2005(2):153-161.

〔2〕AVCIBAS I,SANBUR B,SAYOOD K,Statistical evaluation of image quality measures[J].Journal of Electronic Imaging,2002,11(2):206-213.

〔3〕WANG ZHOU,BOVIK A C.Modern image quality assessment[M].New York:Morgan and Claypool Publish Company,2006:20-30.

〔4〕Z.Wang,H.R.Sheikh,and A.C.Bovik,”No-reference perceptual quality assessme ment of JPEG compressed images,”in Proc.IEEE ICIP,2002,vol.1,pp.477-480.

〔5〕P.Marziliano,F.Dufaux,S.Winkler,and T.Ebrahimi,”Perceptual blur and ringingm etrics:Application to JPEG2000,”Signal Commun,vol.19,no.2,pp.163-172,2004.

〔6〕H.R.Sheikh,A.C.Bovik,and L.K.Cormack,“No-reference quality asses sment using natural scene statistics:JPEG2000,”IEEE Trans.Image Process.,vol.14,no.11,pp.1918–1927,2005.

〔7〕J.Caviedes and F.Oberti,”A newsharpnessmetric based on local kurtosis,ed geand energy information,”signal Process.:Image Commun.,vol.19,no.2,pp.14 7-161,2004.

〔8〕Charrier C,Lebrun G,Lezoray O.Amachine learning-based color image quality metric[C]//Proceedings of Third European Conference on Color in Graphic s.Leeds,UK:Imageing And Vision,2006:251-256.

〔9〕楼斌,沈海斌,赵武锋,严晓浪.基于自然图像统计的无参考图像质量评价[J].浙江大学学报（工学版），2010,44(2):248-252.

〔10〕Moorthy K A,Bovik A C.A two-step framework for constructing blind imag e quality indices [J].IEEE Signal Processing Letters,2010,17(5):513-516.

〔11〕K.Sharifi and A.Leon-Garcia,”Estination of shape parameter for generalized Gaussiandistributions in subb and decompositions of video,”IEEE Tran.Circuit s Syst.Video Technol.,vol.5,no.l,pp.52-56,Feb.1995.

〔12〕V.Vapnik,The Nature of Statistical Learning Theory.Berlin,Germany:Springer Verlag,2000.

〔13〕Sheikh H R,Wang Z,Cormack L,et al.Live image quality assessment databas e release 2[EB/OL].[2007-6-30].http://live.ece.utexas.edu/.

〔14〕A.Srivastava,A.B.Lee,E.P.Simoncelli,and S.-C.Zhu,”On advances in statistical modeling of natural images,”J.Math.Imag.Vis.,vol.18,pp.17-33,2003.

〔15〕D.S.Taubman and M.W.Marcellin,JPEG2000:Image Compression Fundamental s,Standards,and Practice.Norwell,MA:Kluwer,2001.

〔16〕E.P.Simoncelli,”Statistical models for images:Compression,restoration and syn thesis,”presented at the IEEEAsilomar Conf.Signals,Systems,and Computers,Nov.1997.

〔17〕R.W.Buccigrossi and E.P.Simoncelli,”Image compression via joint statistical characterization in the wavelet domain,”IEEE Trans.Image Process.,vol.8,no.12,pp.1688-1701,Dec.1999.