行星式双面研磨轨迹均匀性研究*

杨金双,朱祥龙2

(1.中国工程物理研究院机械制造工艺研究所,四川绵阳 621900; 2.大连理工大学精密与特种加工教育部重点实验室,辽宁大连 116024)

行星式双面研磨轨迹均匀性研究*

杨金双1,朱祥龙2

(1.中国工程物理研究院机械制造工艺研究所,四川绵阳 621900; 2.大连理工大学精密与特种加工教育部重点实验室,辽宁大连 116024)

蓝宝石(α-Al2O3)是一种机光电性能优良的功能晶体材料,在半导体和光电子等行业得到了广泛的应用。行星式双面研磨是蓝宝石基片平面加工的重要手段,加工过程中磨粒轨迹的均匀性对工件的加工精度和表面质量有着重要的影响。通过运动学分析建立了双面研磨磨粒轨迹方程和速度方程,提出一种基于Matlab离散统计的磨粒轨迹均匀性定量评价方法,并求取设定参数下双面研磨轨迹分布均匀性的方差值。

蓝宝石;双面研磨;研磨轨迹;轨迹均匀性;统计分析

0 引 言

蓝宝石(α-Al2O3)具有优良的物理、机械、光学和电学等特性,是观察窗口、LED衬底和电子产品面板生产制造的理想材料,在半导体和光电子行业等领域具有广泛的应用和广阔的发展前景[1-2]。蓝宝石是一种典型的硬脆材料,加工难度大,质量要求高。目前,蓝宝石基片的生产流程主要包括长晶、定向、切片、研磨、抛光等工序[3],其中研磨工序用于去除切片工序中产生的表面损伤,提高工件的面型精度,降低表面粗糙度值,为后续抛光加工奠定基础。行星式双面研磨是获取高平整度平面的加工方法,可获得良好的基片上下表面平行度和片间厚度一致性,在蓝宝石基片研磨加工中得到广泛应用。行星式双面研磨的加工原理如图1所示,放置在游星轮内的工件随游星轮一起在太阳轮和齿圈的差动作用下做行星运动,上、下研磨盘对其两个表面同时进行加工。

双面研磨加工过程中工件表面的磨粒轨迹由上研磨盘、下研磨盘、太阳轮和齿圈的转速共同决定,磨粒轨迹直接影响着工件表面材料的去除效率,工件相对于研磨盘的运动轨迹影响着盘面的磨损情况。在双面研磨轨迹均匀性研究方面,磨粒相对于工件的运动轨迹均匀性和工件相对于研磨盘的轨迹均匀性的研究对改善工件的加工精度和表面质量有重要的意义。

图1 双面研磨加工原理图

笔者提出了一种基于Matlab离散统计的轨迹均匀性定量分析评价方法,通过运动学分析建立了双面研磨磨粒相对于工件的轨迹方程和速度方程,借助于磨粒轨迹的均匀性分析过程,详细阐述了轨迹均匀性定量评价方法。该方法也可用于单面研磨、单面抛光和双面抛光等过程轨迹仿真的均匀性评价。

1 双面研磨运动学建模

双面研磨加工中,工件由游星轮带动,一边绕太阳轮做公转运动,一边绕游星轮轴线做自转运动,太阳轮、齿圈、上研磨盘和下研磨盘绕共同的轴线各自旋转,在上研磨盘部件的重力和外部施加的压力作用下对工件的两个表面同时进行研磨加工。建模过程中,假设工件和游星轮位置相互固定,磨粒相对于工件的研磨轨迹即为磨粒相对于游星轮的轨迹。表1列出了各运动构件的运动参数。

表1 行星式双面研磨中各构件运动参数

在回转平面,建立在磨盘上固定的坐标系O1X1Y1,在游星轮上建立坐标系O2X2Y2。设太阳轮半径为r1,游星轮半径r2,则O1和O2间的距离为l= (r1+r2)。在磨盘上选任意一点 A,A点初始位置距O1点长度RA,O1A与O1X1轴的正向夹角为α。利用图形变换法[4](如图2所示)求解A点相对于游星轮的轨迹方程,得:

图2 磨粒轨迹方程图形变换过程

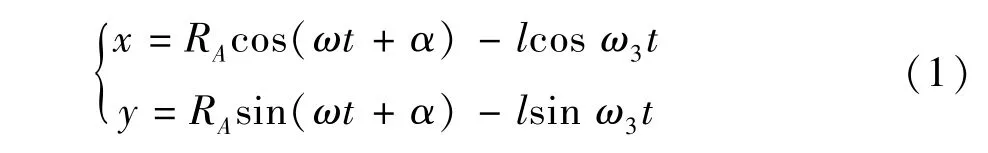
对时间t求导可得到A点的运动速度:

其中:

由磨粒的轨迹方程可知,磨粒的轨迹由磨粒的位置、太阳轮转速、齿圈转速、磨盘的转速共同决定。已有的研究结果表明,磨粒的位置影响着轨迹的分布范围,对轨迹均匀性基本上没有影响[5]。因此,在研磨轨迹的均匀性研究中,重点研究太阳轮、齿圈和磨盘的转速比对研磨轨迹均匀性的影响规律。

2 磨粒轨迹均匀性评价过程

将磨粒轨迹方程和各参数输入到Matlab中绘制轨迹图形,时间t的选取使轨迹线完整覆盖画布,所绘制轨迹图形如图3所示。实际加工中工件常沿游星轮外缘放置,均匀性分析只考虑工件实际放置区域,如图中两个圆形中间环状区域所示,外圈圆表示游星轮分度圆,内部圆表示工件本体内边缘所形成的包络圆。以坐标原点为起点沿纵、横轴方向将图幅分成若干正方形区域,每间隔时间Δt取一个点,以点代表轨迹线,每个点的坐标不同,归属于不同的正方形区域。对各正方形区域内的点的数量进行统计分析,从而给出轨迹均匀性的定量评价。考虑到轨迹线上各处的速度并不相等,等时间间隔所采集的数据点在轨迹上并不是等距离分布,通过判断相邻点之间的距离并插入新点进行修正使统计分析结果更趋近于真实情况。下面以φ100 mm蓝宝石基片的加工为例进行计算。

图3 磨粒轨迹分布

2.1 参数选定

选取参数:齿轮模数m=2.1167 mm;太阳轮转速n1=50 r/min,齿数z1=160;齿圈转速n2=40 r/min,齿数z2=560;游星轮齿数z3=200;研磨盘转速n0=40 r/min,并使RA=381 mm,α=0。运行时间设置为135 s。游星轮半径为211.67 mm,蓝宝石基片沿游星轮外缘放置,轨迹分析时只考虑半径100～210 mm之间的区域。

2.2 速度分析与插值

在上述参数下分析磨粒的速度变化,将式(2)输入到Matlab中,计算磨粒速度并分别绘制x方向、y方向和总速度曲线,如图4所示。由图可知,磨粒的速度呈周期性变化,周期长度约为1 s。最大速度为5.19 m/s,最小速度为2.32 m/s。时间步距Δt设置为1 ms,共采集数据点135 001个,相邻点之间距离最大约为5.19 mm,最小为2.32 mm,差值为2.87 mm。相邻数据点之间的轨迹可近似看成直线,则数据点之间距离的差值越小,数据点在轨迹线上分布越均匀,统计分析的结果就越准确。对数据点修正时以0.23 mm(相邻点最小间距的1/10)为步长,如两点之间距离为2.63 mm则将其分成12段,在其间均匀插入11个点。插值修正后共获取数据点2 273 515 个,相邻点之间距离最大约为0.24 mm,最小为0.22 mm,差值为0.02 mm。正方形区域的边长设置为20 mm,插值后相邻点距离的差值(0.02 mm)、相邻点的距离(最小0.22 mm)和区域边长(20 mm)分别处在三个不同数量级上,数据结果具有较高的可信度。通过改变时间步距、插值步长和正方形边长可以调整仿真分析的精度。

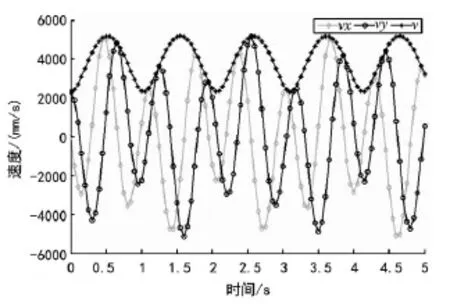
图4 磨粒运动速度分布

2.3 边界处理与统计分析

以坐标原点为起点沿x、y方向划分正方形网格,并建立矩阵数组,矩阵中每一个元素对应着一个正方形网格。通过数据点的坐标判断数据点所属正方形区域并使用该正方形对应的矩阵元素进行计数,计数完毕后再令完全处于研究区域(R=100～210 mm环带)外的正方形网格外对应的矩阵元素为0,与研究区域有交集的正方形网格内的所有点(部分点并不在R=100～210 mm环带内)都参与统计分析。统计完成的数据形式矩阵如图5所示。

提取矩阵内所有不等于0的元素,共获取数据点340个,对这些数据进行统计学分析,求取方差值为122.23,该方差值定量表述了磨粒轨迹的分布均匀程度。改变各回转运动的转速比,磨粒的轨迹也会发生变化,通过对比各不同转速比下轨迹点分布均匀性方差,为双面研磨工艺参数优化提供理论依据。

图5 研究区域点分布数据矩阵

3 结 语

研磨轨迹的分布均匀性对于研磨加工的效率和质量有着重要的意义,并影响着后续抛光加工。笔者通过对双面研磨进行运动学分析和建立轨迹、速度方程,详细地介绍了一种基于Matlab离散统计的轨迹均匀性定量评价方法,并用该方法给出了特定参数下研磨轨迹的分布均匀性方差,解决了长期以来行星式双面研磨轨迹仿真分析优化中无法准确定量评价轨迹分布均匀性的问题。该方法也可用于摆动、直线式单面研磨、单面抛光和行星式双面抛光等过程轨迹仿真的均匀性评价,并依据评价结果对工艺参数的选取进行优化。

[1]臧江龙.单晶蓝宝石基片固结磨料机械化学抛光技术[D].大连:大连理工大学,2013.

[2]Jinshuang Yang,Xianglong Zhu,Zhigang Dong,et al.Design of Double-sided Polishing Machine for Functional Crystal Substrate [J].Advanced Materials Research,2014(1017):580-585.

[3]Li Z C,Pei Z J,Funkenbusch P D.Machining processes for sapphire wafers:a literature review[J].Proceedings of the Institution of Mechanical Engineers,Part B:Journal of Engineering Manufacture. 2011(225):975-989.

[4]刘建河,杨建东.用图形变换法研究行星机构双面研磨轨迹[J].长春理工大学学报,2002,25(2):40-42.

[5]杨金双.蓝宝石基片双面磨削机床结构设计与分析[D].大连:大连理工大学,2015.

Research on Uniform ity of Trajectory in Planetary Double-Side Lapping Process

YANG Jin-shuang1,ZHU Xiang-long2
(1.Institute ofMachinery Manufacturing Technology,China Academy ofEngineering Physics,Mianyang Sichuan 621900,China;2.Key Laboratory for Precision&Non-traditional Machining ofMinistry of Education,Dalian University of Technology,Dalian Liaoning 116024,China)

Sapphire is a kind of functional crystalmaterialwith excellent properties and widely used in the semiconductor and optoelectronic industry.Planetary double-side lapping is one of themost importantmethods in processing sapphire,themachining precision and surface quality of work pieces are affected by the uniformity of abrasive trajectory significantly.In this paper,trajectory and velocity equations of abrasive are set up through the kinematical analysis of double-side lapping,and then a quantitative evaluationmethod of trajectory uniformity based on the Matlab discrete statistics is presented.With thismethod,variance value of abrasive's trajectory uniformity under given parameters is calculated and offers reference for the optimization of double-side lapping parameters.

sapphire;double-side lapping;trajectory;uniformity;statistics and analysis

TG581

A

1007-4414(2015)06-0041-03

10.16576/j.cnki.1007-4414.2015.06.016

2015-09-02

杨金双(1988-),男,河南南阳人,硕士,助理工程师,研究方向:磨削与研磨加工。