基于ANSYS软件的漏磁检测有限元仿真

章合滛，薛建彬，方灿娟

（南京航空航天大学 机电学院，南京 210016）

漏磁无损检测速度快，检出率高，操作简单，不需要对试件进行打磨、清洗、除锈，可在复杂的环境下进行检测，因而在无损检测领域得到了广泛的应用［1］。用传统的物理试验方法研究各种形状缺陷的漏磁场信号特征具有很大的局限性，很难获得大量的实测数据以用于缺陷的定量检测［2］。目前漏磁场的分析主要有基于磁偶极子模型的解析法和数值方法，由于磁偶极子模型存在一定的局限性［3］，所以漏磁场分析主要采用数值方法，其中应用最广泛的数值方法是有限元法。通过有限元分析可以得出缺陷漏磁场的空间分布，将有限元数值仿真分析和试验结果进行比较，最终为试验提供理论依据，扩展了试验能力［4］。目前漏磁场的有限元研究以二维有限元法居多，而实际漏磁场是三维的，这使得二维有限元法存在很大的不足［5－6］。采用三维有限元法对漏磁场进行研究，获得了二维有限元法分析无法获得的信息，使得分析结果更准确、更接近实际情况。实际漏磁检测中，试件端部存在检测盲区，笔者提出一种在端部添加试件引体的方法解决该问题。

1 漏磁检测原理及其ANSYS 电磁场仿真验证

漏磁检测的基本原理［7－8］：铁磁性材料在磁化装置的磁化下，假如没有缺陷，则磁感应矢量绝大部分被束缚于材料内，如果试件有缺陷，因为铁磁性材料的导磁性和缺陷处空气的导磁性相差很大，磁力线将发生弯曲，使得部分磁感应矢量漏出材料外，此时利用探头对试件表面的漏磁场进行检测，把漏磁场转换成缺陷信号（探头线圈里产生的感应电压），经过对缺陷信号进一步分析和处理，就可确定是否存在缺陷，以及缺陷的具体信息。利用ANSYS二维电磁场仿真来验证漏磁检测原理。验证模型为一个通电线圈对铁芯进行磁化，通过对比有无缺陷状态下的磁感应矢量图，对漏磁检测原理进行验证。假设空气的磁导率是常量，用有限的空气来模拟无限空气外场［9］。设置好材料属性后，利用自由网格划分，给线圈施加相同电流密度后进行分析，在后处理器中显示磁感应矢量图。如图1所示，局部放大后对比可以发现，如果铁芯没有缺陷，则大部分磁感应矢量被束缚于壁内，而在有缺陷模型中，虽然大部分磁感应矢量都被束缚于壁内，但同时有少部分磁感应矢量从缺陷处漏出（箭头所指处），从而漏磁原理得到验证。同时可以看出，基于ANSYS的电磁场分析对漏磁场的研究是有可行性的。

2 三维漏磁场

2.1 理论基础及三维模型的建立

图1 磁感应矢量图

电磁场现象的研究是以麦克斯韦方程组作为理论依据的。电磁场微分方程的求解中，只有在边界条件和初始条件的限制下，电磁场才有确定解。电磁场问题的实际求解过程中，边界条件可以概括为三种：狄利克莱（Dirichlet）边界条件、诺依曼（Neumann）边界条件以及它们的组合［10－11］。漏磁检测三维模型的建立中，首先是磁化方式的选择。相比于单线圈对试件进行磁化，双线圈开路磁化方式结构上采用了两个磁化线圈，在两个磁化线圈中通入方向相同大小一致的直流电，磁化和检测效果好，检测时相应装置将检测元件慢慢贴近试件表面，模型如图2 所示。依照三维模型图在ANSYS里建模，其中试件的尺寸为40 mm×40 mm×100mm，两个线圈为矩形线圈，长宽厚为80mm×80mm×2mm，两个线圈中心相距60mm。以模型中心为圆心建立半径R为70mm 的空气层，其中空气的相对磁导率设置成1，试件的材料为ANSYS材料库自带的54号钢，为了方便在缺陷上方1mm的平面内读取漏磁场强度，在缺陷上方建立40mm×1mm×100mm 的空气层，这部分空气采用映射网格划分以便在指定点取值，其余空气和试件采用自由网格划分，空气最外层表面MAG 参数设置成零以模拟无限的空气，最后ANSYS根据麦克斯韦方程组以及相应的边界条件进行求解。

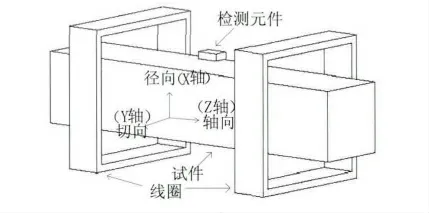
图2 漏磁检测模型

2.2 无缺陷试件磁感应分布情况

在试件无缺陷的情况下，利用ANSYS求解后，在后处理器里可以观察到如图3所示的磁感应矢量图。可以看出，试件内部的磁感应强度很高，大部分磁感应矢量被束缚于壁内。在试件外围由于空气的磁导率很低，磁感应强度迅速衰减到零。同时在试件两端端部，存在明显的磁力线散射现象，使得一般磁敏传感器饱和，漏磁场信号被淹没，从而形成了试件漏磁检测端部的检测盲区。

图3 无缺陷下的磁感应矢量图

2.3 有缺陷试件漏磁场三维分量分布情况

将缺陷布置于图3所示试件上表面的正中心，缺陷的尺寸为径向深度1mm，切向宽度4mm，轴向长度16mm，施加在两个磁化线圈的安匝数为6 000A·N。

2.3.1 漏磁场径向分量分布情况

ANSYS求解后，在径向方向上离试件表面上方1mm 处提取漏磁场径向分量强度。以缺陷中心为原点，切向方向和轴向方向的取值范围分别－2～2mm、－10～10 mm。图4（a）是漏磁场径向分量分布情况，图4（b）是相应的伪彩色图。从图中可以看出，在缺陷正中心上方1mm 处径向分量Bx接近于零，在轴向方向上向两端大致呈线性增加，在两边端部出现正负峰值。从图4（b）可以看出，同一轴向位置在切向方向上磁感应强度也相应增加，不过增加幅度小，在切向方向两端达到了同一轴向位置上的峰值。

2.3.2 漏磁场轴向分量分布情况

同样地，在径向方向上离试件表面上方1 mm处提取漏磁场轴向分量强度，以缺陷中心为原点，切向方向和轴向方向的取值范围分别为－1～1mm、－4～4mm。图5（a）是漏磁场轴向分量分布情况，图5（b）是相应的伪彩色图。从图中可以看出，漏磁场轴向分量关于Y＝0 对称。缺陷正上方中心点的漏磁场轴向分量最大，围绕中心点，在小区域内向四周减小。从轴向方向来看，离开中心点依次出现两个波谷和两个波峰。

图4 漏磁场径向分量分布情况及其伪彩色图

图5 漏磁场轴向分量分布情况及其伪彩色图

2.3.3 漏磁场切向分量分布情况

在径向方向上离试件表面上方1mm 处提取漏磁场切向分量强度，以缺陷中心为原点，切向方向和轴向方向的取值范围分别－2～2 mm、－10～10mm。图6（a）是漏磁场切向分量分布情况，图6（b）是相应的伪彩色图。从图中可以看出，相比于径向分量和轴向分量，漏磁场切向分量小了很多，一般磁敏感元件无法拾取，而且容易受到扰动，这就是工业上漏磁检测基本上不以漏磁场的切向分量作为缺陷的判断依据的原因。从图中还可以看出，漏磁场关于中心点大致呈奇对称，在缺陷上方1mm中心点处接近零。在y～z平面上出现4个正负峰值，其中第一象限和第三象限为正值，第二象限和第四象限为负值。

图6 漏磁场切向分量分布情况及其伪彩色图

3 缺陷几何参数对漏磁场的影响

缺陷的漏磁信号与施加的外部磁场强度、材料的性质、缺陷的尺寸（长、宽、深）、传感器的提离值和位置等诸多因素有关。在保证其他参数不变的基础上，采用同一种磁化结构尺寸，分析缺陷几何参数对缺陷漏磁场分布的影响规律。如图7所示，由于铁磁性材料的导磁性和缺陷处空气的导磁性相差很大，磁力线在缺陷处将发生弯曲，使得部分磁力线漏出管壁。由于漏磁场的切向分量很小且容易受到扰动，故此处不予研究。因此将缺陷漏磁场模型简化成二维模型，并将漏磁场分解为轴向分量和径向分量。可以明显看出，在缺陷中心的正上方，此处只存在轴向分量，所以总磁感应强度应与轴向分量一致。但由于网格划分的影响，使得切向分量和径向分量微量存在。现对缺陷中心正上方1mm 的总磁感应强度以及轴向分量进行分析。

图7 缺陷漏磁场模型

3.1 缺陷径向深度对漏磁场的影响

缺陷布置于试件上表面正中心，保持缺陷轴向长度和切向宽度为4mm×4mm 不变，深度变化范围为0.1～6mm。在缺陷中心点上方1mm 处提取漏磁场。图8（a）为总磁感应强度随径向深度的变化趋势，图8（b）为漏磁场轴向分量随径向深度的变化趋势。从图中可以看出，总磁感应强度随径向深度变化的趋势与轴向分量随径向深度变化的趋势是基本一致的，而且总磁感应强度与轴向分量的大小也基本相同，这也验证了开头作的假设。从图中还可以看出，在0.1～4mm 深度范围内，总磁感应强度和轴向分量的大小都随着深度的增加而大致呈线性增加，但之后，深度的增加反而降低了总磁感应强度以及轴向分量的大小。这说明，双线圈开路磁化方式的漏磁检测适合于一定深度缺陷的检测，对大深度缺陷还是难以提供准确的判断依据。

图8 缺陷径向深度对漏磁场的影响

3.2 缺陷切向宽度对漏磁场的影响

保持缺陷径向深度和轴向长度4 mm×4 mm不变，切向宽度的变化范围为0～7mm。在缺陷中心点上方1mm 处提取漏磁场。图9（a）为总磁感应强度随切向宽度的变化趋势，图9（b）为漏磁场轴向分量随切向宽度的变化趋势。从图中可以看出，总磁感应强度和轴向分量随切向宽度变化的趋势基本一致，大小也基本相同。在0～4mm 宽度范围内，总磁感应强度和轴向分量的大小都随着宽度的增加而大致呈线性增加，但之后，随着宽度的增加，总磁感应强度和轴向分量的大小不会一直增加，而是出现波动。这也说明，双线圈开路磁化方式的漏磁检测适合于一定宽度的检测，对大宽度缺陷的检测难以提供准确的判断依据。对比图8和图9的斜率可以看出，在一定范围内，相比于深度，总磁感应强度和轴向分量对缺陷宽度的变化更敏感。

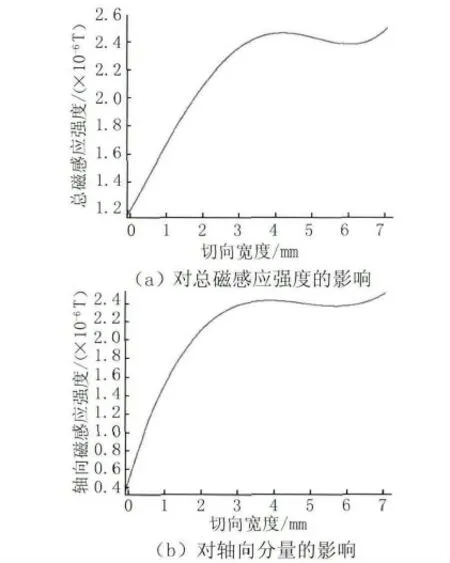
图9 缺陷切向宽度对漏磁场的影响

3.3 缺陷轴向长度对漏磁场的影响

保持缺陷径向深度和切向宽度4 mm×4 mm不变，轴向长度的变化范围为0～7mm。在缺陷中心点上方1mm 处提取漏磁场。图10（a）为总磁感应强度随轴向长度的变化趋势，图10（b）为漏磁场轴向分量随轴向长度的变化趋势。从图中可以看出，总磁感应强度和轴向分量随轴向长度变化的趋势基本一致，大小也基本相同。在0～1mm 的轴向长度范围内，总磁感应强度和轴向分量随着长度的增加大致呈线性增加。但随着轴向长度的进一步增加，总磁感应强度和轴向分量表现的没有规律性。这说明，双线圈开路磁化方式的漏磁检测适合于小轴向长度的检测，对大长度缺陷的检测也难以提供准确的判断依据。

图10 缺陷轴向长度对漏磁场的影响

4 电流强度对漏磁场的影响

保持缺陷尺寸不变，分析只改变激励电流大小对漏磁场的影响，电流安匝数的取值范围为6 000～12 000A·N，间隔1 000A·N 取值一次。在缺陷中心点上方1mm 处提取漏磁场，如图11所示，总磁感应强度与激励电流基本成正比关系。要想得到比较大的缺陷漏磁场峰值，理应增大激励电流大小，但是在实际检测时，激励电流不可能无穷大，且激励电流过大，磁敏传感器检测漏磁场时容易达到饱和，导致输出波形失真，影响缺陷的识别能力。电流的增大伴随着激励模块的功耗也变大，同时容易导致线圈发热，影响检测效果。实际检测系统中，应根据实际检测条件和需要，合理选择电流大小。

5 试件端部漏磁检测盲区的解决方法

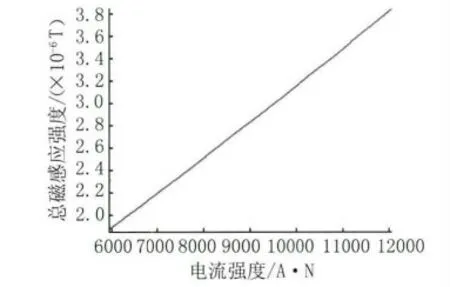
图11 电流强度对总磁感应强度的影响

如图3所示，当试件被磁化时，端部存在明显的磁力线散射现象，使得一般磁敏传感器饱和，漏磁场信号被淹没，因而形成了漏磁检测试件端部的检测盲区。如图12所示，提出一种在端部添加试件引体的方法来解决端部的检测盲区。试件引体的材料与被测试件一致，图13为添加试件引体后的仿真结果。对比图3和图13可以看出，添加引体后，端部产生的高强度散射磁感应矢量基本被引体所吸附，剩余的散射磁感应强度很微弱，不足以影响端部的漏磁检测。从仿真结果可以看出，在端部添加试件引体可以很好地解决试件端部的检测盲区。

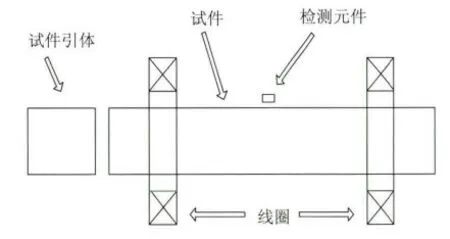
图12 端部检测盲区解决方案

图13 添加引体后的磁感应矢量图

6 结语

首先采用二维电磁场仿真验证了漏磁检测原理，又采用三维有限元法研究缺陷漏磁场，弥补了传统物理实验方法需要大量人力物力的缺憾。同时研究了缺陷几何参数和磁化电流强度对漏磁场的影响，并提出一种解决漏磁检测试件端部检测盲区的方法。三维有限元法克服了二维有限元法分析时存在的问题，获得了二维有限元法分析无法获得的信息，使得分析结果更准确、更接近实际情况，为实现漏磁检测的定量化打下了基础。

［1］纪凤珠，王长龙，陈正阁，等.基于三维有限元法的漏磁场分析［J］.兵工学报，2007，28（7）：876－879.

［2］李莺莺，靳世久，魏茂安.管道漏磁法检测的ANSYS仿真研究［J］.无损检测，2005，27（2）：72－75.

［3］李路明，张家骏，李振星，等.用有限元方法优化漏磁检测［J］.无损检测，1997，19（6）：154－158.

［4］Zhen－mao CHEN，MIHALACHE G，PREDA O，et al.Reconstruction of crack shapes from the MFLT signals by using a rapid forward solver and an optimization approach［J］.IEEE Transactions on Magnetics，2002，38（2）：1025－1028.

［5］刘志平，康宜华，武新军，等.大面积钢板局部磁化的三维有限元分析［J］.华中科技大学学报，2003，31（8）：10－12.

［6］LI Y，WILSON J W，TIAN G Y.Experiment and simulation study of 3D magnetic field sensing for magnetic flux leakage defect characterization［J］.NDT＆E International，2007，40（2）：179－184.

［7］林俊明.漏磁检测技术及发展现状研究［J］.无损检测，2006，30（1）：1－5.

［8］丁战武，何仁洋，刘忠.管道漏磁检测缺陷信号的仿真分析与量化模型［J］.无损检测，2013，35（3）：30－33.

［9］Al－NAEMI F I，HALL J P，MOSES A J.FEM modelling techniques of magnetic flux leakage－type NDT for ferromagnetic plate inspections［J］.Journal of Magnetism and Magnetic Materials，2006，304（2）：790－793.

［10］G DARIUSZ，MARTIN L.Culpepper.Modeling 3D magnetic fields for precision magnetic actuators that use non－periodic magnet arrays［J］.Precision Engineering，2008，32（2）：134－142.

［11］吴先梅，钱梦騄.有限元法在管道漏磁检测中的应用［J］.无损检测，2000，22（4）：147－150.