运筹学在现代物流中的应用

刘会茹 张红梅

（1.石家庄经济学院数理学院，河北 石家庄 050031；2.石家庄学院数学与信息科学系，河北 石家庄 050035）

1 问题的提出

随着中国社会主义市场经济体系的建立,世界经济一体化进程的加快和科学技术的飞速发展,物流产业成为国民经济中的一个新兴的产业部门,被称为是继原材料、劳动力之外的“第三利润的源泉”.随着现代物流的发展,物流方案的选择和优化决策在如何更好的利用物流资源和满足用户自身的需求方面起着日益重要的作用.而运筹学通过广泛应用现有的科学技术知识和数学方法能很好的解决物流活动中提出的问题,为决策者选择最优的物流决策提供定量分析的依据.

2 运筹学与物流学

2．1 运筹学

运筹学是运用系统科学的方法,通过建立数学模型,协助得出最优决策的一门应用性学科.它主要研究对有限的人、财、物、时、空、信息等资源进行合理筹划和运用,寻找管理及决策最优化等问题,它根据问题的需要,建立数学模型,经过分析运算,得出合理安排,以达到更经济、更有效地配置人力、物力、财力等资源的目的.随着国民经济和科学技术的飞跃发展,运筹学也在不断的发展完善,成为现代应用数学中最重要的一个分支.运筹学以数学为工具,从系统的观点出发研究全局性的规划,寻找各种物流问题的最优方案和最适宜的可行解,在现代物流中的应用越来越广泛,在辅助物流活动决策、物流合理化建设中发挥着重要作用,取得了良好的经济效益.

2.2 物流学

物流是一个内容广泛而且复杂的大系统,现代物流配送不仅是送货,它是将信息、运输、仓储、库存、装卸搬运以及包装等物流活动综合起来的一种新型的集成式管理,其任务是尽可能降低物流的总成本,为顾客提供最好的服务,是以满足消费者的需求为目标,把制造、运输、销售等市场情况统一起来考虑的一种战略措施.

2．3 物流学与运筹学的关系

物流学与运筹学作为一门正式学科都始于20世纪40年代的第二次世界大战,从一开始两者就是相互渗透,交叉发展的.运筹学是用来解决最优资源配置,而物流是追求一种快速、及时、节约、库存合理的服务,运筹学正是物流优化的工具,是系统理论在物流中应用的具体方法,从这一点来看,两者不谋而合.

3 运筹学在现代物流中的主要应用

运筹学在早期主要应用于军事科学.随着科学技术和生产的发展,运筹学已渗入到许多领域,如社会经济领域,交通运输业,民政事业等,而且发挥着越来越重要的作用.运筹学主要包括数学规划、图论、存储论、排队论、对策论、决策分析、网络流、可靠性数学理论、搜索论、模拟等等.运筹学在现代物流中已经被广泛利用,解决了许多实际问题,也取得了很好的效果.

3.1 规划论

规划论是运筹学的一个主要分支,包括线性规划、非线性规划、整数规划、目标规划、动态规划等,它是在满足给定约束要求下,按一个或多个目标来寻求最优方案的数学方法.在现代物流中,线性规划常用来解决人员分配和物资调运、配送等问题,整数规划用来求解完成工作所需的人数、机器设备台数和厂库的选址等,动态规划用来解决最优路径、资源分配、库存控制、生产调度、设备更新等问题.

（1）线性规划

线性规划是目前在现代物流中应用最广泛的一种优化方法,它的理论已经非常成熟,可以应用于生产计划、物资调用、资源优化配置等问题.它主要研究两类问题：一类是在有限的劳动力、设备、资金等资源条件下,研究如何合理安排生产计划,以获取最大的经济效益；另一类是为了实现某一特定的目标(生产指标或其它指标),研究如何组织生产,如何合理安排工艺流程等等,使得消耗的资源(人力、设备台数、资金原材料等)最少.线性规划可通过单纯形法求出最优解,现在已有专门的软件,使用起来非常方便.

（2）动态规划

动态规划是运筹学的一个分支,是一种解决多阶段决策过程最优化的数学方法,它把复杂的多阶段决策问题分解成一些相互关联的比较容易解决的单阶段决策问题,通过解决这些单阶段决策问题来解决多阶段决策问题,以寻求最优决策序列的方法.在现代物流方面,动态规划可以用来解决资源分配问题、库存问题、生产调度问题、设备更新问题、生产过程最优控制问题、最优路径问题、装载问题、排序问题等等,它是现代物流管理中的一种重要的决策方法.

3．2 图论

图论是一个古老的但又十分活跃的分支，它是网络技术的基础.图论的创始人是数学家欧拉,1736年他发表了图论方面的第一篇论文，解决了著名的哥尼斯堡七桥难题.相隔一百年后,1847年基尔霍夫第一次应用图论的原理分析电网,从而把图论引进到工程技术领域.20世纪50年代以来,图论得到进一步发展,将庞大复杂的工程系统和管理问题用图描述,可以解决许多工程设计和管理决策的最优化问题,图论引起数学家、工程技术人员及企业决策者的重视.

图论在现代物流中也有很多的应用,如运输问题、物流网点间的物资调运和车辆调度时路线的选择、配送中心的送货、逆向物流中产品的回收等,需要应用图论中的最小生成树、最短路、最大流、最小费用流等知识来求得运输所需时间最少或路线最短或费用最省的路线；在工厂、仓库、配送中心等物流设施的选址问题上,物流网点内部工种、任务、人员的指派问题上,设备更新问题上,可以运用图论知识帮助决策者进行最优的安排.

3．3 排队论

排队是日常生活中经常遇到的现象,如顾客到商店去买东西,病人到医院看病,当售货员、医生的数量满足不了顾客或病人及时服务的需要时,就出现了排队现象.作为管理人员,就要把排队时间控制在一定的限度内,在提高服务质量和降低成本之间取得平衡,找到最适当的解.排队论就是解决这类问题的一门科学,它广泛地用于解决诸如电话局的占线问题,车站、机场、码头等交通枢纽的堵塞与疏导,故障机器的停机待修,水库的存储调节等有形无形的排队现象的问题.

排队论在现代物流中有着广泛的应用,如仓库保管员和物流机械维修人员的聘用数量问题,如何既能保证仓储保管业务和物流机械的正常运转,又不造成人力资源浪费；又如机场跑道设计和机场数量问题,如何既保证飞机起降的使用要求,又不浪费机场的资源；再如码头的泊位设计和装卸设备的配置问题,如何既能满足船舶到港的装卸要求,而又不浪费港口资源.这些问题都可以用排队论的方法加以解决.

3．4 存储论

存储论又称库存论,是研究经营生产中各种物资应当在什么时间,以多少数量来补充库存,才能使库存和采购的总费用最小的一门学科,它在提高系统工作效率、降低产品成本上有重要作用.

存储论主要用来解决多种物资库存量的管理,确定某些设备的能力或容量,如某仓库库存能力的大小,某港口码头的转运能力,车载量的大小等等.合理应用存储论,不但可以节省实际运行费用,而且能减少资源的开销,比如减少管理人员、提高转运设备的使用率、减少运输、装卸设备等等.

3．5 对策论

对策论又称博弈论,它是在竞争场合下,双方或多方如何针对对手采取策略的一种定量分析方法.在人类的活动中,这种竞争的场合很多,例如，军事上的战斗,政治上的较量以及普通生活中的下棋,竞赛等,就连孩子们之间的游戏也是最简单的对策,比如以手势进行的“剪刀，石头，布”的游戏.

现代物流业充满了竞争,对策论可以帮助我们寻找最佳的竞争策略,以便战胜对手或减少损失.例如某城市有两个配送中心经营相同的业务,为争夺市场份额,双方都有多个策略可供选择,可以运用对策论加以分析,寻找最佳策略.再如某地区的汽车运输公司要与铁路系统争夺客源,有多种策略可供选择,也可用对策论研究竞争方案.

3．6 决策分析

决策分析是人们生活和工作中普遍存在的一种活动,是为处理当前或未来可能发生的问题选择最佳方案的一种过程.比如某企业对某种新产品的市场需求状况不十分清楚,可能有好、中、差三种情况,市场好就能获利,中等情况就不赔不赚,情况差就要亏本,到底投不投产,就需要决策分析.

现代物流中的决策就是在充分占有资料的基础上,根据物流的客观环境,借助于科学的数学分析、实验仿真或经验判断,在已提出的若干物流方案中,选择一个合理、满意的方案的决策行为.例如制定投资计划、生产计划、物资调运计划、选择自建仓库、租赁公共仓库、自购车辆或租赁车辆等.

4 实例分析

设有三个化肥厂供应四个地区的农用化肥.除第四个地区不宜用第三个厂生产的化肥外,假定各厂的化肥在这些地区使用的效果是一样的.各化肥厂的年产量、各地区的年需求量以及各化肥厂到各地区运送化肥的单价如表1.试求出总费用最少的化肥调拨方案.

解 这是一个规划问题,管理层的目标是将化肥采用最优的物流方案进行运输和配送,使总的物流费用达到最小.解这个问题的困难是不知道每个地区的化肥需求量究竟是多少.根据题意只知道各地区需求量的上限和下限.但在求解运输规划问题时要求各点的需求量是固定的.下面我们来看如何处理这样的问题.

1）首先假定取消最低需求量的限制,而把最大需求量当做各地区的需求量,那么第四个地区的最大需求量是多少呢？根据题意是无限大.但从实际来看,三个产地的总产量是160万吨.如果满足其他三个地区的最低需求,即30+70+0=100万吨,那么供应第四个地区的最大量也不过是160-100=60万吨.所以第四个地区的最大需求量只能是60万吨.这样四个地区的最大需求量分别是50,70,30,60万吨,共计210万吨.而三个产地的总产量是160万吨,所以供小于求.这时要假设一个虚产地(第四个产地),其产量为210-160=50万吨.

2）下面来看如何满足各地区的最低需求.以第一个地区为例.它的最低需求量是30万吨,最大需求量是50万吨.为此,我们把需求量分成两部分.第一部分为30万吨,第二部分为20万吨.为了保证第一部分的30万吨化肥全部从实产地获得,令从虚产地向该地区第一部分运输的单价为M.这样就保证了第一个地区的最低需求量.而第二部分,则根据优化结果,可以从实产地获得,也可以从虚产地获得.其它地区的情况均可按上述方法处理,于是得到表2.

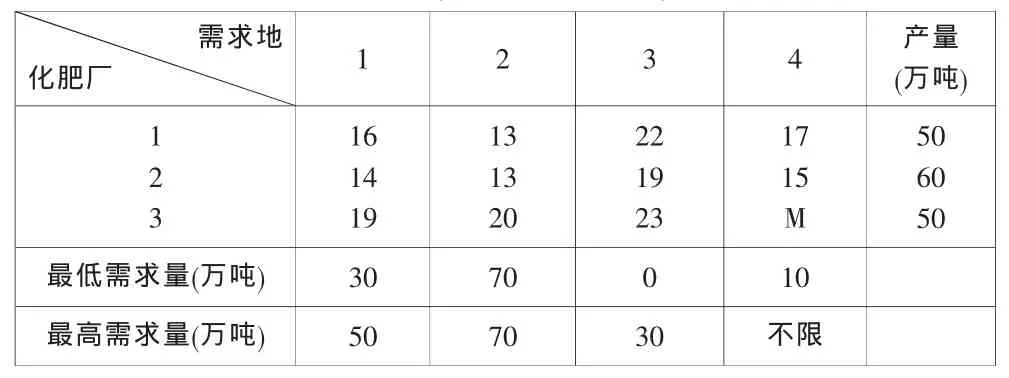
表 1 (运价：万元/万吨)

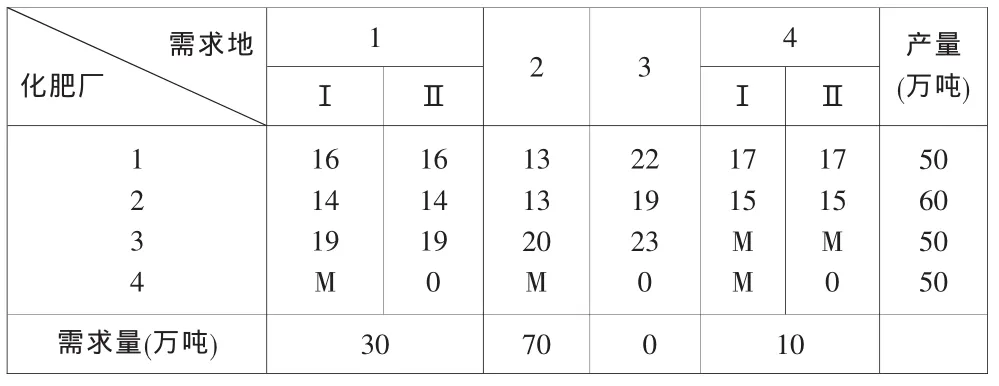
表2

用最小费用法可以找到初始基本可行解,根据计算出的检验数,经过三次迭代便可求得最优解,得到最佳运输方案是x12=50,x22=20,x24=40,x31=30+20=50(其中xij表示第i个化肥厂向第j个地区运送化肥的数量),总费用为 z=50×13+20×13+40×15+50×19=2460(万元).

5 结语

物流活动的实质是通过人们的各种物流活动,使物质资料从供应地向需求地移动.物流管理方法的目标是将各种物流活动进行整合,从而实现其综合效益.而现代物流管理所呈现的复杂性也不是简单算术能解决的,以计算机为手段的运筹学理论是支撑现代物流管理的有效工具.物流业的发展离不开运筹学的技术支持.运筹学是系统工程学和现代管理科学中的一种基础理论和不可缺少的方法,它的应用将会使物流管理更加高效快捷.

［1］宁宣熙.运筹学实用教程[M]．北京：科学出版社,2002.

［2］孔造杰.运筹学 [M]．北京：机械工业出版社,2006.

［3］曹勇,周晓光,李宗元.应用运筹学[M]．北京：经济管理出版社,2008.

［4］韩柏棠.管理运筹学[M]．北京：高等教育出版社,2007.

［5］宋伟刚.物流工程及应用M]．北京：机械工业出版社,200.