In n N(n=1~13)团簇的几何结构和电子性质
2015-01-10李勇
李 勇
(河南质量工程职业学院,河南 平顶山 467000)
0 引言
原子团簇可看作各种物质由原子分子向大块物质转变过程中的特殊物相,引起了人们极大的兴趣。III族氮化物,如BN,AlN,GaN和InN是很重要的半导体材料,在微电子和光电子领域均显示出广阔的应用前景,这导致了人们在理论和实验上对其结构、电子性质和光学性质的大量的研究。BN的电子谱已被理论和实验调查,并且基态结构已经被确定[1-4]。随着对凝聚态物质理论研究的系统和深入,以及AlN,GaN薄膜材料研究的进展,对AlN,GaN团簇以及以AlN,GaN为簇合物骨架系列的研究多有报导[5-7]。在理论方面,许多理论工作者计算了AlN[8-16]和GaN[11-24]团簇的几何结构和电子结构。
InN同其它的III族氮化物AlN和GaN相比,被认为是低损耗高效电池、光学掩膜及多种传感器的优选材料[25]。相对于GaAs和GaN,InN具有优越的稳态和瞬态电子输运特性,这些特性使得InN在高频率,高速率晶体管的应用上有着非常独特的优势[26-27]。此外InN在太赫兹(THz)辐射中有很好的应用前景,在热光伏系统中则可作为等离子体滤波器材料等[28-31]。Jones et al.[32]利用分子束外延(MBE)技术生长InN,并进行了不同程度的Mg掺杂,结果Mg掺杂InN样品内部呈现出较强的p型特征。一些工作者[33-37]利用现代谱学实验方法来测量InN的带隙。最近,Petravic et al.[38]通过软X射线吸收谱研究了N缺陷InN的电子结构。尽管InN材料有很多优良特性,然而这些研究主要集中在晶体材料上,这些材料在微电子和光电子等方面的应用要求对其团簇分子的物理和化学性质有足够的了解。然而关于InN团簇的研究却很少。Zhou and Andrews[6]采用用Laser-Ablated方法得到了InN、NInN和In3N团簇的红外谱图。理论上对InN团簇的报道也仅限于有限的几个小的InnN(n=1~3)团簇的研究。Kandalam et al.在密度泛函理论的基础上运用非局域密度近似的方法计算了InnNm(n,m=1~2)[11-12]和(InN)n(n=3~6)[13-14]团簇的结构和稳定性,Costales et al.[15-17]用密度泛函理论对(InN)n(n=1~6)中性和阴离子团簇的几何结构,电子性质及化学键合进行了研究。
本文利用密度泛函理论中的广义梯度近似(GGA)对InnN(n=1~13)团簇的几何结构、电子性质和化学键合进行了系列的探讨,其结论对于理解小尺寸团簇的形成机理及稳定性规律和寻找更大尺寸团簇的理论研究可提供有意义的参考,这对进一步合成新的特殊功能光电材料都有一定的意义。
下面的论文做如下组织:第二部分给出计算方法的简要描述,结果在第三部分,主要结论被总结在第四部分。
1 计算方法
本章中,计算采用的仍然是密度泛函方法,所用的计算程序包是Dmol3软件包[39],使用广义梯度(GGA)近似泛函[40-41]。计算过程中,我们用Dmol3软件中的自旋极化密度泛函方法进行充分的几何优化。在电子结构计算中,采取全电子相对论效应和包括d极化的双数基组,交换关联相互作用采用GGA-PW91方法,自洽场收敛标准为10-6Hartree。为了加速自洽场收敛我们使用了DIIS方法,轨道计算中使用的smearing标准为0.005 Hartree。在几何优化过程中,力的收敛标准是0.002 Hartree/Å,位移收敛标准0.005Å,能量收敛标准10-5Hartree。在计算的过程中采取自旋非限制方法。为了确定得到的最低能量构型是势能面上的极小点,在结构优化过程中对振动频率进行了计算,得到的最稳定构型均无虚频。
在团簇物理学中,最基本的问题就是寻找团簇的基态构型。为了寻找到InnN(n=1~13)团簇的最低能量结构,对每一尺寸的团簇,我们考虑了大量的可能初始结构。虽然InnN团簇的研究很少,然而对于AlN[8-16]和GaN[11-24]团簇却有大量的报道,因此在具体选取团簇初始构型时,我们先参考AlnN和GanN团簇的平衡构型进行优化计算。另一方面,InnN团簇的可能初始结构也用下述的方法得到,先通过In替代稳态的和亚稳态的纯Aln[42]和Gan[42-43]团簇中Al和Ga原子,然后就是在以上所得结构基础上用N原子戴帽、填充和置换。并且,在计算所得小InnN团簇的平衡构型基础之上,通过移动和添加In和N原子得到初始结构进行优化。而且,我们也考虑了一些具有高对称性的结构做为初始构型。然后在PW91/DND理论水平上进行几何优化,并同时计算频率。
2 结果与讨论
2.1 团簇的几何结构
图1和图2给出了InnN团簇的平衡几何结构,其中深色小球代表N原子、浅色小球代表In原子,结构按能量由低到高依次标为n a、n b、n c…。表1中给出了InnN基态团簇的对称性,In-N平均键长d,在N位置的Mulliken电荷qN等参数。
InN单体基态的平均结合能为1.062eV,振动频率为386.310cm-1。没有实验值可对比。这一结果与Kandalam et al.的计算结果(1.040eV,378.000cm-1)[11]符合的很好,而振动频率比 Zhou和 Andrews[6]的结果(481.500cm-1)偏低。InN单体基态的键长(2.245Å)与Kandalam et al.(2.280Å)[11]和 Costales et al.(2.270Å)[12,16]的结果是一致的,比 Zhou和Andrews[6]的结果(2.040Å)稍长一点。In2N团簇的最低能量结构(图1,2a)是In-N键长2.033Å,具有C2V对称性的准线性N-In-N结构。在三聚体In2N中N-In间的距离比单体短0.212Å。这一键长与Kandalam et al.(2.010 Å)[11],Costales et al.(2.016 Å)[12,16]和 Zhou 及其合作者 (1.950Å)[6]的结论符合的很好。In3N团簇的最低能量结构 (图1,3a)是一个中心N粘合三个In原子的等边三角形结构(D3h),N-In键长为2.143Å,比Zhou和Andrews[6]的值(2.098Å)稍长。 对于In4N,最低能量结构(图1,4a)是N周围有四个In环绕的具有D4h对称性的平面四边形结构,N-In键长2.275Å,比In3N中N-In键长长,归因于In4N中N原子更多的配位数(四边形平面四配位数)。对于In5N,最低能量结构(图1,5a)是In4N中In-In边戴帽一个In原子而得的具有C2V对称性的平面结构,另一亚稳态构型(图1,5b)是N原子位于底面中心的扭曲的四棱锥(Cs),在能量上比基态高0.024eV。
对于n>4的InnN基态团簇,随着尺寸的增加,三维结构开始流行。In6N的最低能量结构(图1,6a)是一个三棱柱,其中N原子具有近四边形平面四配位数,N原子这种四边形平面四配位数也出现在In4N和In5N的基态构型中。In6N另一个简并的异构体是一个畸变的八面体结构(图1,6b),比基态结构能量仅高0.007eV。一个平面结构In6N的异构体(图1,6c)也被得到,其能量高于基态0.818eV。In原子面戴帽In6N八面体结构(图1,6b)得到In7N(图 1,7a)的基态结构。 In8N的最稳定结构(图1,8a)是一个N原子位于中心的管状结构(C3V)。从7a和8a中可以看到,存在一个类In6N八面体结构单元。另一个具有C2V对称性的In8N的亚稳态结构(图1,8b)可看做双面戴帽八面体结构,它的能量高于基态0.038eV。进一步戴帽In原子,相继到得了In9N和In10N的最低能量结构(图2,9a,10a),两种结构都展现出In6N八面体单元,并且周围的In原子像流行的金属结构那样聚集在该八面体单元附近。一个具有D2d对称性的异构体(图2,10b)也被得到并且它的能量高于基态0.172eV。

图1 In n N(n=1~8)团簇的平衡结构(黑圆和灰圆分别代表N和In原子)
从图2、图3中可以看到,In6N八面体单元普遍存在于n=7~11的InnN团簇基态结构中,然而,在In11N基态团簇(图2,11a)中,In6N八面体单元发生了严重地扭曲。对于In11N,两个亚稳态结构也被得到,在11b中存在In4N四边形平面结构,11c则是可看作10a结构的继续生长,在能量上分别比基态高0.032和0.042eV。对于n=12的基态,12a和12b是两个简并的结构,前者对称性为C1,能量上仅比后者低0.002eV,后者具有Cs的对称性,两个平衡结构中都有一个In4N四边形平面单元。12c是N原子被包裹在中心的亚稳态结构,在能量上比基态高0.200eV。N原子位于中心的一个二十面体结构(图2,12d)也被考虑,该结构是不适合的,在该结构中最邻近N-In间的平均距离2.928Å,大于N和In原子的半径之和(2.750Å),在能量上比基态高0.540eV。对于In13N,最低能量结构(图2,13a)是Cs结构,N配位数是四,最邻近NIn间的平均距离为2.269Å。13b是存在有In4N四边形平面单元的结构,平均最邻近N-In间距是2.325Å,在能量上高于基态0.240eV。

图2 In n N(n=2~13)团簇的平衡结构(黑圆和灰圆分别代表N和In原子)

表1 In n N团簇基态结构的对称性,平均最近邻N-In间距(d N-In)和在N位置的Mulliken电荷q N
目前的计算结果表明InnN团簇结构的生长显现出有趣的生长方式。对于n=1,2,InnN团簇的最低能量结构是线性的,n=3~5是二维平面结钩,n=6~13则是三维结构。关于N原子的配位数,n=1~4显现出较简单可能配位数。 n=4,5,6a,11b,12a,12b 存在有 In4N 四边形平面配位单元,n=7,8表现出简单的 3D配位,n=9,10,11c则有 In6N八面体单元,聚集在周围的In原子则表现出金属团簇常采用的结构方式,n=13,N原子再次表现出四配位数,13a中有一个6b单元,而6b与三棱柱状的6a基态结构可看作是简并的。InnN团簇结构增长的方式是与组成原子的泡利半径及原子间化学键的相对强度息息相关的。In泡利半径比N原子大,对于双原子系统,In-In比N-In键结合弱,而且,在氮化物团簇中,较多N原子配位数能增强N-In键结合的强度[14,17],结果,为了提高体系的稳定性,N-In间很乐意保持这种In4N平面配位单元或者In6N八面体配位单元。而且,对于二十面体结构的12d,N比In的泡利半径小得多,这就是说N不能成为中心原子是因为较大的NIn间距离。
2.2 团簇的稳定性
为了确定团簇的相对稳定性,我们计算InnN(1≤n≤13)团簇最低能量结构的平均结合能Eb和总能的二阶差分(Δ2E),平均结合能和总能的二阶差分定义如下:

式(1)和(2)中E表示基态团簇的总能量。InnN(n=1~13)团簇最低能量结构的平均结合能Eb和总能的二阶差分(Δ2E),如图3,图4所示。

图3 In n N和Ga n N(n=1~13)基态团簇的平均结合能E b随团簇尺寸的变化
从图3中可以看出,InnN和GanN团簇的平均结合能随团簇尺寸n的变化趋势是一致的[23]。团簇的平均结合能在1≤n≤3时迅速增加,在3≤n≤5逐渐减小,从n=5开始缓慢的增大,在n=7和9出现了两个小峰,表明In7N和In9N比邻近的团簇稳定。最大的峰值出现在n=3处,是由于In3N的最低能量结构是N原子位于中心的三角形结构,而这种结构很稳定,Ⅲ族氮化物团簇Al3N[8-9]和Ga3N[23]的最低能量结构也是这种稳定的三角形结构。
在团簇物理学中,二阶能量差分△2E能敏感地反映团簇的稳定性[44],二阶能量差分值越大,说明团簇的稳定性越高。图4展现出△2E随团簇尺寸的变化情况,最大的值出现在n=3、7、9处,表明这些团簇具有较高的稳定性,这与图3平均结合能变化情况是相一致的。对于InnN团簇而言,n=3、7、9较稳定是因为In3N是第一个采取非线性的结构,In7N是第一个N原子采取非平面配位数的结构,In9N则是第一个包含In6N结构单元,且N周围的In原子象流行的金属结构一样分布。InnN团簇的二阶能量差分随团簇尺寸的变化奇偶振荡,奇数n的InnN团簇比偶数的稳定,而n=5、11时则出现了例外,是由于In5N中,In原子松散的附着在In4N的In-In边,而在In11N结构中,In6N的八面体单元已发生了严重的扭曲,n=11~12,InnN团簇是从包含In6N八面体单元到包含In4N的四边形平面单元的过渡,结果导致In5N和In11N团簇的稳定性降低。
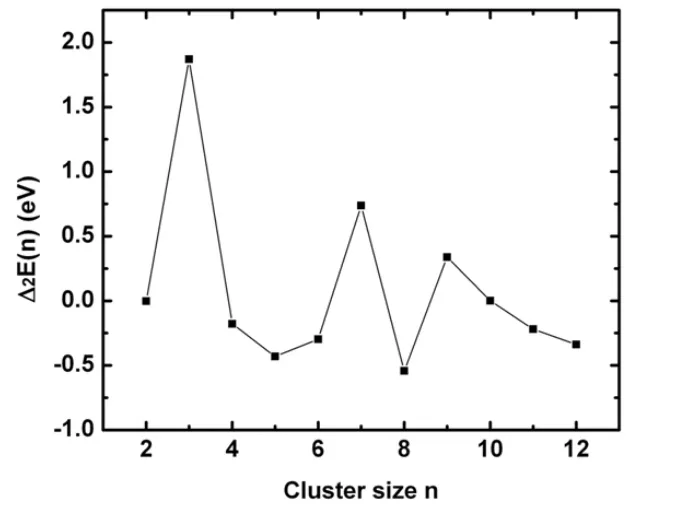
图4 In n N(n=2~12)基态团簇的二阶能量差分Δ2E随团簇尺寸的变化
2.3 HOMO-LUMO能隙,垂直电离势和垂直电子亲和势
对于半导体材料来说,禁带与导带之间的能量间隔是非常重要的参数,那么对于半导体团簇来说这个数据可以用最高占有轨道和最低非占有轨道(HOMO-LUMO)的能量间隙来反映。从图5中看到,InnN团簇的HOMO-LUMO能隙随团簇尺寸n的增加奇偶振荡。除了n=5,奇数n的InnN团簇具有较大的能隙,而偶数n的InnN团簇的能隙较小,这主要归咎于电子对效应,奇数n的InnN团簇有偶数个价电子,比偶数n的InnN团簇稳定性高。从图5可以看到,InnN团簇的能隙值的变化范围是从0.504-2.557eV,InnN团簇能隙的奇偶振荡趋势也在GanN团簇观察到[23],比较GanN、InnN团簇能隙的奇偶振荡趋势发现,除了n=2,偶数n的InnN团簇能隙值比GanN的大,而奇数n的InnN团簇的能隙值都比GanN的小。我们分析了s,p,d轨道的态密度和最高占据轨道(HOMO)及最低未占据轨道(LUMO)的等电荷密度分布图(图6)。结果发现HOMO和LUMO主要是In的p和d电子以及N的p电子所贡献,来自s电子的贡献很少,因此pd杂化是这种效应产生的主要原因。从图6中可能看出,HOMO和LUMO的电荷密度主要分布在In原子周围,在N原子周围分布的也有一些。HOMO和LUMO能隙Eg的大小反映了电子从HOMO向LUMO发生跃迁的能力,在一定程度上代表了团簇分子参与化学反应的能力,除了In5N外,奇数n的InnN基态团簇的能隙比较大,表明化学活性较低,这也说明奇数n的InnN基态团簇相对比较稳定。
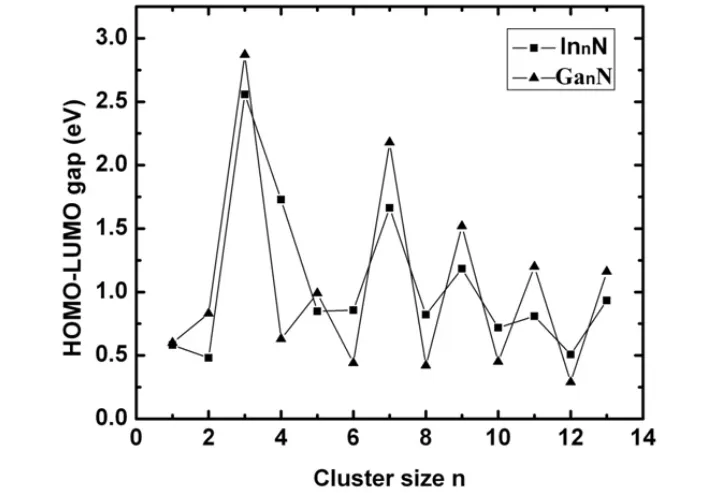
图5 In n N和Ga n N(n=1~13)基态团簇的HOMO-LUMO能隙(E g)随团簇尺寸的变化

图6 In n N(n=1~13)基态团簇的的HOMO和LUMO
对于InnN团簇的最低能量结构,我们进行了Mulliken 布居分析,在N位置的电荷如表1所示。在所有的InnN团簇中,N是带负电荷的,电荷总是从In向N原子转移,n=1~3,向N转移的电荷急剧增加,在In3N中,向N转移的电荷达到了最大值-1.048e,然后随着团簇尺寸的增加,N位置的电荷轻微的减少,表明团簇的金属性逐渐地增强。如表1所示,我们也注意到对于n=2,3,4,在In位置的电荷分别是0.401e,0.316e,0.219e,并且相似的情况也出现在尺寸较大的团簇中,这说明InnN团簇仅有很小的离子性。在表1中也给出了InnN团簇的平均N-In键长,N-In间平均距离的变化范围是2.033~2.440Å,且随着N原子配位数的增加而单调增加。然而InN单体中N-In间距却比In2N中平均N-In间的距离长,在InN单体中,N-In键共价性很小,有较少的电荷转移,极化也小,In-N间相互作用主要是静电性的。另一方面,In2N是准线性分子,In-N间电荷转移比单体多,较多的电荷转移使得N-In间距减小。这就是为什么随着In原子的增加,N-In间距收缩了[11,16],结果在三原子的In3N团簇中,N-In键合比单体更强。
垂直电离势(VIP)和垂直电子亲和势(VEA)在描述团簇电子结构属性上是很重要的物理量,定义如下:

其中En为InnN中性团簇的总能量,和分别为团簇在中性构型不变基础上阳离子和阴离子的总能量。垂直电离势和垂直电子亲和势随团簇尺寸的变化规律如图7所示。从图7中可以看到,InnN团簇垂直电离势和垂直电子亲和势随团簇尺寸的变化规律同GanN团簇基本上是一致的[23]。InnN团簇垂直电离势在n=1~5,11~13随团簇尺寸的增加单调减小,而在n=6~10奇偶振荡,峰值出现奇数n处。总的来说,垂直电离势随团簇尺寸的增加而下降,这是由于随着InnN团簇金属In原子的增加,团簇的金属属性在增强。至于InnN团簇垂直电离势奇偶振荡方式,这再次是团簇电子对效应的表现。对于同一尺寸的InnN和GanN团簇,后者的垂直电离势的值比前者的大,说明前者的金属性强。从图7中还可看到,除了n=13,偶数n比奇数n的InnN团簇的垂直电子亲和势大,且n=3图簇VEA最小。偶数n的InnN团簇具有奇数个价电子,额外的电子不得不进入邻近的轨道,消耗能量,结果有较高的VEA值。从图7可以看到,InnN(n=1~13)团簇的VIP的变化范围是7.855到5.231eV,而VEA则是0.327到2.266eV。

图7 In n N和Ga n N(n=1~13)基态团簇的垂直电离势(VIP)和垂直电子亲和势(VEA)随团簇尺寸的变化
2.4 结论
本文利用密度泛函理论中的广义梯度近似(GGA)对InnN团簇进行了研究,得到了InnN(n=1~13)团簇最低能量结构及亚稳态结构,计算了最低能量结构的平均结合能,二阶能量差分,在N位置的密立根电荷,垂直电离势,垂直电子亲和势和HOMO-LUMO能隙,并同相关的一些理论结果做了比较,主要结论总结如下:
(1)我们研究了 InnN(n=1~13)基态团簇的生长模式,n=1~2,InnN基态团簇是线性的,n=3~5,是平面型的,n=6~13,则是三维结构。 n=6~10,较大的InnN基态团簇是通过在小的Inn-1N基态团簇的基础上面戴帽In原子生长而成,其中每一结构都含有一个In6N的八面体单元。n=11~13,InnN基态团簇结构的主旨则是从含有一个In6N的八面体单元向N原子具有四配数的结构过渡。
(2)通过对InnN基态团簇的平均结合能和总能的二阶能量差分分析可得,n=3,7,9的InnN基态团簇比邻近的团簇有较高的稳定性。
(3)通过分析在N位置的密立根电荷,结果表明对于小的InnN团簇,N-In键合具少许的离子性,随着团簇尺寸的增加,InnN团簇的金属性越来越显著。
(4)计算表明,InnN(n=1~13)基态团簇的 HOMO-LUMO 能隙,垂直电离势(VIP)和垂直电子亲和势(VEA)随团簇尺寸的变化奇偶振荡。总的来讲,VIP随尺寸的增加而减小,VEA随尺寸的增加而增大。同尺寸的InnN和GanN基态团簇的VIP相比较小,表明InnN比GanN团簇的金属性强。
[1]G.Verhaegen,W.G.Richards,and C.M.Moser,J.Chem.Phys.46,160(1967);O.A.Mosher and R.P.Frosch,ibid.52,5781(1970).
[2]M.P.Melrose and O.Russell,J.Chem.Phys.55,470(1971).
[3]J.C.M.Martin,J.P.Francois,and R.Gijbels,J.Chem.Phys.90,6469(1989).
[4]M.Lorenz,J.Agreiter,A.M.Smith,and V.E.Bondybey,J.Chem.Phys.104,3143(1996).
[5]J.D.Simmons and J.K.McDonald,J.Mol.Spectrosc.46,58(1972).
[6]M.Zhou and L.Andrews,J.Phys.Chem.A 104,1648(2000).
[7]H.J.Himmel and N.Hebben,Chem.-Eur.J.11,4096(2005).
[8]S.K.Nayak,S.N.Khanna,and P.Jena,Phys.Rev.B 57,3787(1998).
[9]B.H.Boo and Z.Liu,J.Phys.Chem.A 103,1250(1999).
[10]L.Andrews,M.Zhou,G.V.Chertihin,W.D.Bare,and Y.Hannachi,J.Phys.Chem.A 104,1656(2000).
[11]A.K.Kandalam,R.Pandey,M.A.Blanco,A.Costales,J.M.Recio,and J.M.Newsam,J.Phys.Chem.B 104,4361(2000).
[12]A.Costales,A.K.Kandalam,A.M.Pendas,M.A.Blanco,J.M.Recio,and R.Pandey,J.Phys.Chem.B 104,4368(2000).
[13]A.K.Kandalam,M.A.Blanco,and R.Pandey,J.Phys.Chem.B 105,6080(2001).
[14]A.K.Kandalam,M.A.Blanco,and R.Pandey,J.Phys.Chem.B 106,1945(2002).
[15]A.Costales,M.A.Blanco,A.M.Pendas,A.K.Kandalam,and R.Pandey,J.Am.Chem.Soc.124,4116(2002).
[16]A.Costales and R.Pandey,J.Phys.Chem.A 107,191(2003).
[17]A.Costales,A.K.Kandalam,and R.Pandey,J.Phys.Chem.B 107,4508(2003).
[18]B.Song and P.L.Cao,Phys.Lett.A 300,485(2002).
[19]B.Song and P.L.Cao,Chin.Phys.Lett.20,1488(2003).
[20]B.Song and P.L.Cao,Phys.Lett.A 306,57(2002).
[21]B.Song,P.L.Cao,and B.X.Li,Phys.Lett.A 315,308(2003).
[22]B.Song and P.L.Cao,Phys.Lett.A 328,364(2004).
[23]B.Song,C.H.Yao,and P.L.Cao,Phys.Rev.B 74,035306(2006).
[24]Ch.Sh.Wang and K.Balasubramanian,Chem.Phys.Lett.402,294(2005).
[25]S.Strite and H.Morkoc,J.Vac.Sci.Technol.B 10,1237(1992).
[26]S.K.O’Leary,B.E.Foutz,and M.S.Shur,J.Appl.Phys.83,826(1998).
[27]B.E.Foutz,S.K.O’Leary,and M.S.Shur,J.Appl.Phys.85,7727(1999).
[28]E.Starikov,P.Shiktorov,and V.Gružinskis,Physica B (Amsterdam)314,171(2002).
[29]E.Starikov,P.Shiktorov,and V.Gružinskis,Mater.Sci.Forum 384,205(2002).
[30]E.Starikov,V.Gružinskis,and P.Shiktorov,Phys.Status Solidi A 190,287(2002).
[31]Z.G.Qian,W.Z.Shen,and H.Ogawa,J.Appl.Phys.92,3683(2002).
[32]R.E.Jones,K.M.Yu,S.X.Li,W.Walukiewicz,J.W.Ager,E.E.Haller,H.Lu,and W.J.Schaff,Phys.Rev.Lett.96,125505(2006).
[33]L.Tansley and C.P.Foley,J.Appl.Phys.59,3241(1986).
[34]T.Inushima,V.V.Mamutin,V.A.Vekshin,S.V.Ivanov,T.Sakon,M.Motokawa,and S.Ohoya,J.Cryst.Growth 227-228,481(2001).
[35]V.Yu.Davydov,A.A.Klochikhin,R.P.Seisyan,V.V.Emtsev,S.V.Ivanov,F.Bechstedt,J.Furthmüller,H.Harima,A.V.Mudryi,J.Aderhold,O.Semchinova,and J.Graul,Phys.Status Solidi B 229,R1(2002).
[36]J.Wu,W.Walukiewicz,K.M.Yu,J.W.Ager III,E.E.Haller,H.Lu,W.J.Schaff,Y.Saito,and Y.Nanishi,Appl.Phys.Lett.80,3967(2002).
[37]T.V.Shubina,S.V.Ivanov,V.N.Jmerik,D.D.Solnyshkov,V.A.Vekshin,and P.S.Kop’ev,Phys.Rev.Lett.92,117407(2004).
[38]M.Petravic,P.N.K.Deenapanray,M.D.Fraser,A.V.Soldatov,Y.-W.Yang,P.A.Anderson,and S.M.Durbin,J.Phys.Chem.B 110,2984(2006).
[39]B.Delley,J.Chem.Phys.92,508(1990).
[40]J.P.Perdew and Y.Wang,Phys.Rev.B 45,13244(1992).
[41]Y.Wang and J.P.Perdew,Phys.Rev.B 43,8911(1991).
[42]R.O.Jones,J.Chem.Phys.99,1194(1993).
[43]B.Song and P.L.Cao,J.Chem.Phys.123,144312(2005).
[44]G.H.Wang and J.J.Zhao,Phys.Rev.B 64,205411(2001).
