关于埃尔米特插值的教学探讨

2015-01-08王艳

重庆与世界(教师发展版) 2015年3期

王艳

（重庆师范大学数学科学学院，重庆 400047）

插值法是函数逼近的一种重要方法，也是数值计算的最基本的内容。本科数值分析课程中主要涉及到拉格朗日（Lagrange）插值、牛顿（Newton）插值和（Hermite）插值问题，其中Lagrange插值和Newton插值都是用来处理只以节点处函数值为插值条件的多项式的构造，而Hermite插值是用来处理以节点处函数值及其导数值为插值条件的多项式的构造[1]。

Hermite插值问题涉及到导数值，而且解的形式可以有多种，插值条件也可由多种形式给出，因此这部分内容知识点多，方法灵活，学生往往难以抓住方法的实质从而灵活地构造出所求的插值多项式。事实上，Hermite插值问题插值条件的形式基本上可以分为两类，给出所有点处的函数值和导数值或给出所有点处的函数值和某几个点处的导数值。对于这两类插值条件，我们大多采用构造法和“待定系数法”相结合的方式，不过构造的切入点不同。根据插值条件以及具体的求解方式，本文将Hermite插值问题分为直接Hermite插值问题和间接Hermite插值问题，并结合自身教学实践，对这两类Hermite插值问题求解方式的教学进行了探讨。

一、Hermite插值问题

许多实际插值问题中，为了使插值函数能更好地逼近被插值函数，不但要求二者在节点上函数值相等，而且还要求插值函数在某些节点或全部节点上与被插值函数的导数值也相等，甚至要求高阶导数也相等。这类插值问题称作埃尔米特（Hermite）插值问题[2]。此类插值是以法国数学家Charles Hermite命名的，因此引入课堂之前可以适当穿插一小段关于Charles Hermite的人物传记及Hermite插值的产生背景，目的在于增加课堂趣味性，提高学生的学习兴趣。

设已知函数 f（x）在插值区间[a，b]上n+1个互异的节点xi（i=1，2，…，n）处的函数值 f（xi）及其导数值f（pi）（xi）（pi=1，2，…），Hermite插值问题要求构造一个插值函数H（x），使其在节点处的函数值和导数值与 f（x）的函数值和各阶导数值对应相等，即

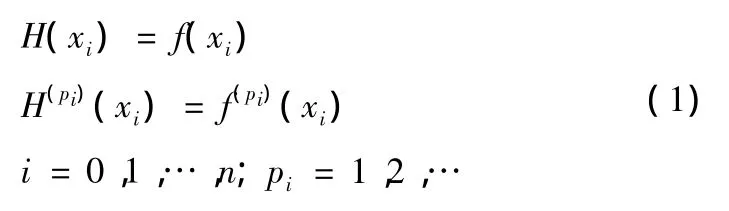
若H（x）是代数多项式，则称H（x）为Hermite插值多项式[2－3]。

特别强调的是，Hermite插值问题解的形式可以有多种，插值条件也可由多种形式给出。例如已知全部节点上的函数值和导数值，或者已知全部节点上的函数值和某几点上的导数值。但不管是哪种情况，只要给出的插值条件数比所要求的多项式次数多一个，该插值问题总是可求解的[2]。Hermite插值多项式的求解，大多采用构造法和“待定系数法”相结合的方式，但对不同形式的插值条件，构造的切入点往往不同。因此，我们可以根据插值条件的形式，将Hermite插值问题分为直接Hermite插值问题和间接Hermite插值问题。

本科课程主要讨论pi=1（i=1，2）这类最简单，但也是最常用的Hermite插值问题。

（一）直接Hermite插值问题

当pi=1时，直接Hermite插值问题是指给出所有节点处的函数值和一阶导数值，问题描述为:

给定函数 f（x）在插值区间[a，b]上n+1个互异的节点xi（i=1，2，…，n）处的函数值 f（xi）及其一阶导数值f′（xi），要求构造一个插值多项式H（x），满足条件

这里给出了2n+2个条件，可唯一确定一个次数不超过2n+1的插值多项式H2n+1（x）=H（x）。

仿照求Lagrange插值多项式的构造基函数的方法，我们可推导出满足插值条件（2）的插值多项式H2n+1（x）的表达式为[3]

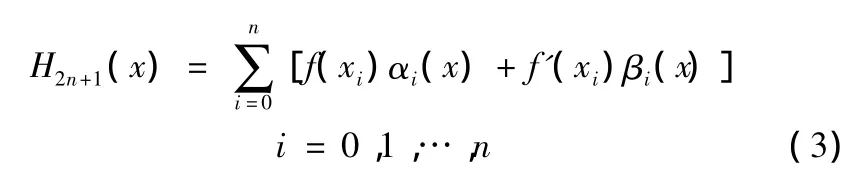
其中

为两类插值基函数，共2n+2个，每一个都是2n+1次的多项式为 Lagrange 插值基函数。

实际使用较多的是三次Hermite插值多项式，此时n=1，节点有两个x0和x1，计算公式为

对于直接Hermite插值问题（2）的求解，可以直接套用公式（3）或（5）。但需要指出的是，插值条件必须给出所有节点处的函数值和一阶导数值，如果所给出的函数值和导数值不是关于节点对等的，那么此类插值多项式的构造就无法直接套用公式，教学过程中可以给出两个实例来具体说明。

（二）间接Hermite插值问题

如果Hermite插值条件给出的是n+1个互异的节点上的函数值和某几个点上的导数值，所要求的Hermite插值多项式无法直接套用上一节的公式，但因涉及到函数的导数值仍属于Hermite插值问题，我们称之为间接Hermite插值问题。

对于这类插值问题的求解，我们通常先根据插值条件的个数确定插值多项式的次数，然后利用其中某几个条件构造一个低于所求多项式次数的Newton插值多项式、Lagrange插值多项式或Hermite插值多项式，并利用余下的条件确定出待定多项式的系数。下面举例说明:

例若 f（x）在[0，2]上有五阶连续导数，试求满足条件

的插值多项式H（x）。

分析该问题的求解有多种方式，比如可以先利用三个节点处函数值的条件构造Newton插值多项式、Lagrange插值多项式，或者先利用前两个节点的函数值和导数值构造Hermite插值多项式，然后根据余下的插值条件确定待定多项式的系数。

解法1 由给定的5个插值条件，显然可确定一个次数不超过4次的Hermite插值多项式H（x）。由前3个插值条件，可构造节点0，1，2上的二次Newton插值多项式

显然，N2（x）满足插值条件 N2（xi）=f（xi）（xi=0，1，2），而H（x）也满足插值条件:H（xi）=f（xi）（xi=0，1，2），由此可知函数H（x）－N2（x）以xi（xi=0，1，2）为零点且次数不超过4次，故可设

其中，a，b为待定多项式的系数。

于是，所求的插值多项式H（x）可表为如下形式

下面，利用余下的插值条件 H′（0）=f′（0）=0，H′（1）=f′（1）=1 来确定 a，b。为此，对上式求导得

分别令x=0，x=1代入，整理可得

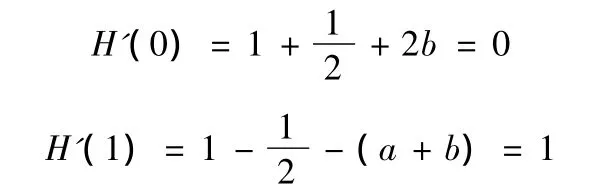
于是有

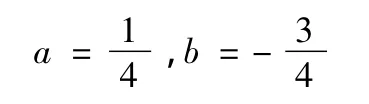
将a，b的值代回H（x）的表达式即得所求的插值多项式为

因为上式是结合Newton插值多项式构造的，所以也称为Newton-Hermite插值多项式。当然也可先采用Lagrange插值多项式构造L2（x），再令

H（x）=L2（x）+（ax+b）（x-0）（x-1）（x-2）同样可得到满足相同插值条件的H（x）的另一种形式

上式也称为Lagrange-Hermite插值多项式。

解法2 先由插值条件

构造节点0，1上的三次Hermite插值多项式

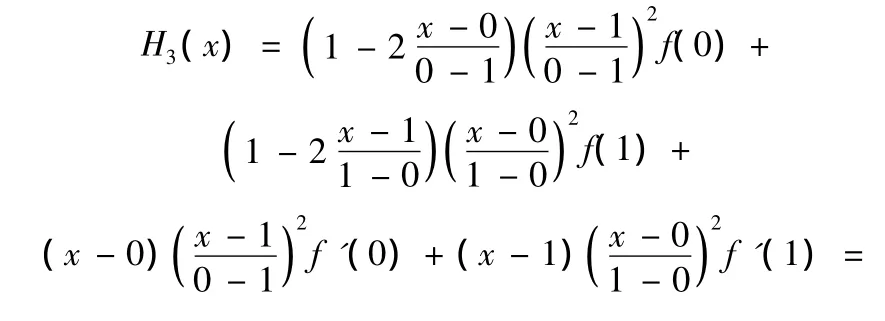
由于H3（x）满足插值条件H3（xi）=f（xi），H′3（xi）=f′（xi）（xi=0，1），而 H（x）也满足插值条件 H（xi）=f（xi），H′（xi）=f′（xi）（xi=0，1），所以可知函数 H（x）－H3（x）以xi（xi=0，1）为二重零点且次数不超过4次，故可设

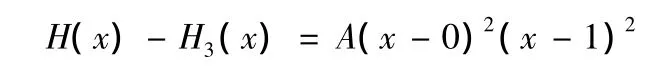
其中，A为待定常数。

于是，所求的插值多项式H（x）可表为如下形式

下面，利用余下的插值条件H（2）=f（2）=1来确定A。令x=2代入上式，计算可得

将A的值代回H（x）的表达式即得所求的插值多项式为

二、两个注解

注解1 事实上，对于满足插值条件（1）的一般情形的Hermite插值多项式的构造仍可以采用上述构造基函数的方法[4]，但这不是唯一方法，比如可以仿照Newton插值多项式的构造方法，利用差商的非构造性定义[5]来构造Hermite插值多项式[6]，建议有兴趣者查阅文献[4，6 －7]进行扩展阅读。

注解2 上例所得的三个插值多项式都是恒等的，只是形式不同，理论依据在于满足插值条件（1）的Hermite插值多项式的存在唯一性。条件（1）中的插值条件共有个，Charles Hermite早在1878年就证明:存在唯一的次数不高于N－1的代数多项式H（x），使得插值条件（1）满足。根据不同的专业要求，对数学与应用数学等理论要求较高的专业可以适当地作一些相关理论知识的延伸。