基于扰动观测器的多旋翼无人机机载云台模糊自适应跟踪控制

王日俊，白 越，续志军，宫 勋，张 欣，3，田彦涛

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.中国科学院大学，北京100039；3.长春工程学院电气与信息工程学院，吉林长春130012；4.吉林大学通信学院，吉林长春130025）

基于扰动观测器的多旋翼无人机机载云台模糊自适应跟踪控制

王日俊1，2，白 越1，续志军1，宫 勋1，张 欣1，2，3，田彦涛4

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.中国科学院大学，北京100039；3.长春工程学院电气与信息工程学院，吉林长春130012；4.吉林大学通信学院，吉林长春130025）

为了补偿多旋翼无人机机载云台的扰动，实现机载云台的稳定跟踪控制，提出基于改进扰动观测器的模糊自适应跟踪控制方法.在原有扰动观测器结构的反馈回路中引入一个补偿控制，构建基于速度信号的改进型扰动观测器结构，分析该结构的补偿扰动能力和鲁棒性；利用模糊系统的逼近性质和李雅普诺夫稳定性原理，设计相应的模糊自适应跟踪控制结构，证明了该控制结构的稳定性.飞行实验表明，应用该控制方法后，视轴稳定误差的均方值小于0.02°，跟踪给定位置信号的跟踪误差小于0.08°，完全能够满足多旋翼无人机机载云台的稳定跟踪控制.引入补偿控制后的扰动观测器补偿扰动能力明显提高，提出的控制方法具有较高的稳定跟踪精度.

多旋翼无人机；机载云台；扰动观测器；跟踪控制；模糊自适应；稳定性

多旋翼无人机（multi-motor unmanned aerial vehicle，m UAV）由于机动性强、起降灵活等特点被广泛应用在侦察、目标捕获、识别和跟踪等领域.多旋翼无人机重量轻、体积小，所搭载的机载云台极易受到姿态变化、机体振动、气流扰动、摩擦以及其他未知扰动等因素的干扰，造成机载视频图像模糊、离焦甚至目标从视场中消失[1-2].一方面，容易造成操作人员视觉疲劳引发误操作，甚至无法识别目标信息.另一方面，会导致侦察、跟踪等任务无法完成.对多旋翼无人机机载云台的扰动补偿和稳定跟踪控制的研究和方法改进有着重大的实际意义.

在目前的扰动补偿方法中，Umeno等[3]提出的扰动观测器（disturbance observer DOB）具有较强的扰动补偿能力、运算量小、无需外部传感器等特点，在机载稳定云台的扰动补偿上得到了广泛的应用[4-6].李嘉全等[6]在控制系统中引入了一种扰动观测器结构，对扰动进行估计和补偿，改善了机载稳定平台抑制扰动的能力，但是该结构难以对系统中存在的噪声干扰进行补偿.谢巍等[7]通过新增2个控制器设计一种改进的扰动观测器，并在直流电机系统中验证了抗噪声干扰的鲁棒性能.多旋翼无人机的自身特点决定了机载云台扰动的非线性和强藕合性的特点，因此仅采用扰动观测器结构来对机载云台扰动进行补偿控制，难以取得理想的稳定跟踪效果.模糊系统和神经网络等智能控制策略，因其鲁棒性、实时性好、不依赖系统模型、具有逼近任何函数的性质等优点，已广泛应用于稳定平台的伺服跟踪控制系统中.高篙等[8]针对机载光电跟踪系统构造了基于模糊推理的变论域模糊控制器，保证了系统的性能要求，具有很好的实时性和鲁棒性.朱海荣等[9]利用神经元的自学习和自适应能力，提出基于扰动补偿的单神经元自适应PI控制策略，保证了稳定平台在外界扰动和系统变化时平台的稳定跟踪能力.

本文针对多旋翼无人机机载云台的扰动补偿和稳定跟踪控制要求，提出基于改进扰动观测器的模糊自适应跟踪控制方法.在现有扰动观测器结构的基础上，在反馈回路中引入一个补偿控制结构，提高补偿扰动的能力.利用模糊系统来在线估计机载云台的其他未知扰动，进一步提升机载云台的稳定精度，保证系统的稳定跟踪性能，实现对多旋翼无人机机载云台的扰动补偿和精确跟踪控制.

1 机载云台系统建模

1.1 机载云台建模

假设机载云台是刚体，且旋转中心与云台的质心重合.根据Lagrange-Euler方程[10]可知，忽略离心力和科氏力，云台的非线性模型方程与单关节机构的模型方程一致.

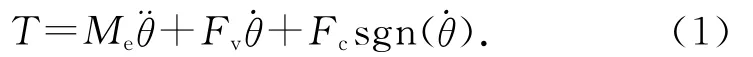
式中：Me为载荷的有效惯量，Fv为黏滞摩擦力（viscous friction），Fc为静摩擦力（Coulomb friction）.将方程中的非线性项Fcsgn看作云台的扰动项Tf，可得机载云台的线性模型为

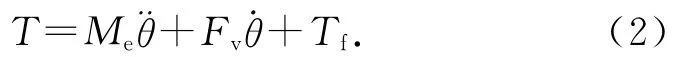
令x1=θ，x2=系统输出y= x1，于是开环系统的空间状态方程为

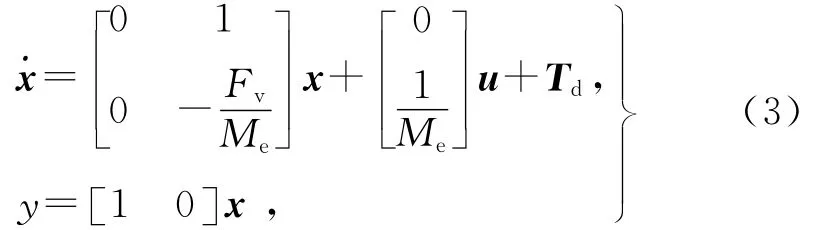
即

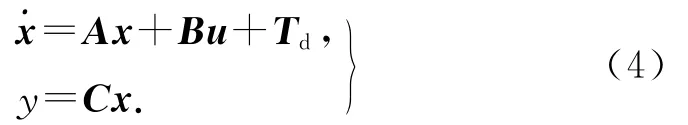
式中：

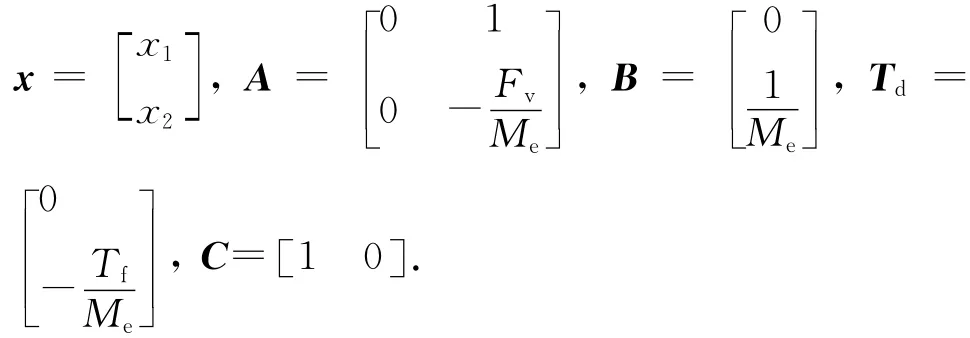
1.2 执行机构建模

该机载云台采用直流电机作为执行机构，数学模型[11]为

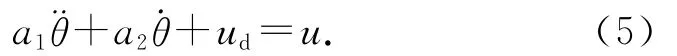
式中：θ为电机的位置角度，ud为扰动，u为控制输出的电压.在实际应用中，a1=+ δa2，其中和为变量a1和a2实际的测量值，δa1、δa2为扰动引起变量a1和a2发生的变化量.定义非线性未知扰动函数f（·）=+ud，f（·）包括模型误差、参数波动、Td以及其他非线性未知扰动等，于是，

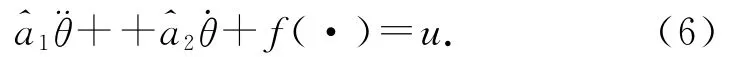
2 基于速度信号的改进型扰动观测器设计

如图1所示为由现有基于速度信号的扰动观测器（velocity based disturbance observer，VDOB）构成的控制结构.

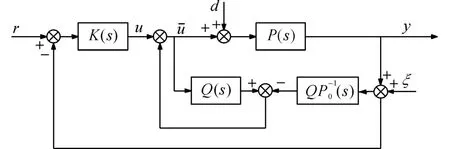
图1 基于v DOB的控制系统结构Fig.1 VDOB-based control system structure

图中，P（s）表示稳定平台模型，P0（s）为平台的标称模型，信号r、d、ξ为系统的参考输入、外界扰动以及噪声干扰.实际上，d和ξ通常处于不同的频率范围，于是有如下假设.

假设1存在2个截止频率ωl、ωh，且ωl＜ωh，噪声干扰处于高频范围内ξ（jω）∈（ωh，∞），外界扰动及参考输入均处于低频范围内，即d（jω）∈（0，ωl），r（jω）∈（0，ωl）.根据图1，可得系统的传递函数为

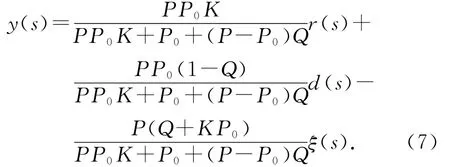
假设2如果在低频范围（0，ωl）内Q（s）≈1，在高频范围（ωh，∞）内Q（s）≈0.系统输出可以近似地表示为

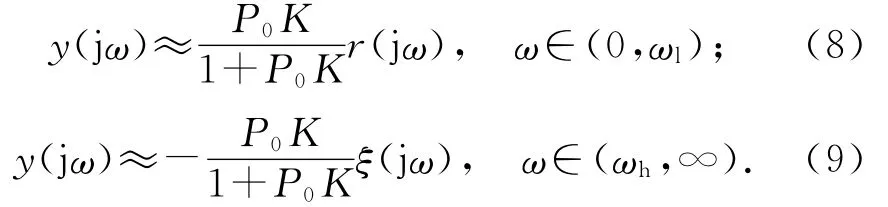
由此看出，基于VDOB的控制结构能够完全消除外界扰动对系统输出的影响，但是对高频噪声干扰的抑制作用不理想.针对上述情形，提出基于速度信号的改进型扰动观测器结构（improved velocity based disturbance observer，IVDOB），如图2所示.与VDOB相比较，在系统输出的反馈信号端增加一个补偿控制器Q2（s）用来补偿系统的高频干扰，提高补偿高频噪声干扰的能力.

根据图2，可得IVDOB的传递函数：

图2 基于Iv DOB的控制系统结构Fig.2 IVDOB-based control system structure

为了既能补偿外界扰动d，又能补偿噪声干扰ξ，Q1、Q2须满足以下2个条件：

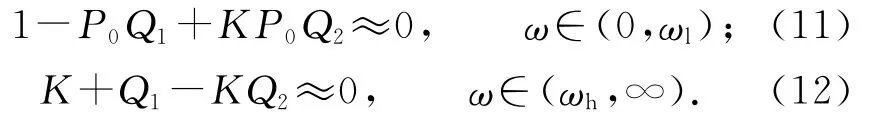
即

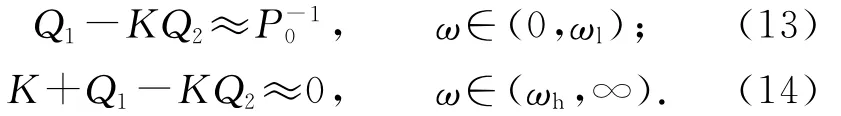
考虑如下情形.

对于标称模型的逆模型存在且稳定时，IVDOB不仅保证了对系统输入很好的跟踪性能，而且完全补偿了系统的低频扰动d.对比式（16）、（9）可知，ξ得到了很好的抑制.

若标称模型P0（s）存在误差，且模型误差的集合可以用加法摄动来表示，即P0（s）=P（s）+W1Δ，其中W1为稳定有界的加权函数，P（s）、Δ（s）为严格有理稳定的函数.由鲁棒稳定性定理可知，IVDOB鲁棒稳定的充要条件为

定理1如图2所示，假设P0（s）∈H∞，控制器K（s）满足P0（s）对于闭环传递函数的稳定性要求，且满足Q1P0+Q2=1时，则参考输入r到控制器K（s）输出u之间的闭环传递函数始终不变.即：Gur（s）=（1+KP0）-1K.

证明：图2中，当d和ξ均存在时，可以得到如下关系式：

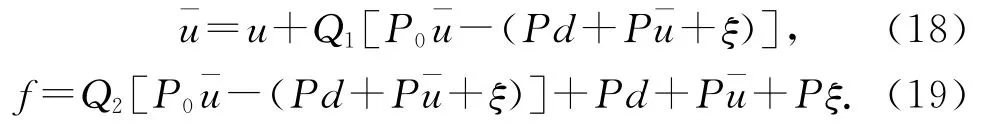
根据式（18）、（19），有

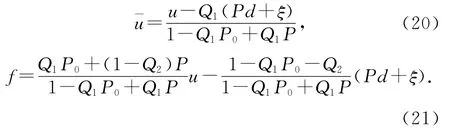
又因为Q1P0+Q2=1，代入式（21）有f=P0u，故Gur（s）=（1+KP0）-1K.定理得证.

3 模糊自适应控制器设计

采用基于IVDOB的控制结构，能够对系统扰动进行补偿，实现对机载云台的视轴稳定控制.扰动观测器的控制方法无法完全补偿系统中存在的扰动，Miller等[12]指出，多旋翼无人机体积小、重量轻，且飞行环境恶劣，在飞行作业过程中存在很多非线性未知干扰，而这些扰动的存在使得机载云台的稳定精度和跟踪性能受到影响.鉴于上述分析，本文利用模糊系统的万能逼近特性来进一步对系统的干扰进行补偿[13]，设计机载云台的模糊自适应控制器，提高了机载云台的稳定精度和跟踪性能.

基于IVDOB的模糊自适应控制结构如图3所示.该控制结构采用双闭环控制结构，其中速度环由IVDOB来控制实现，位置环由PD控制器、前馈控制器、模糊控制器以及鲁棒控制器4部分组成.

模糊规则定义如下.R（j）：ifθ1isandθ2is，then ufis Bj，其中模糊系统的输入=（θ1，θ2）=（θ，∈U，模糊系统输出uf∈R是集合Ui（i=1，2）上的模糊集，Bj（j=1，2，…，N）是集合R上的模糊集.模糊系统根据上述规则，实现了从模糊集U∈R2到R的映射.依据模糊推理系统引理[14]，有

图3 机载云台控制系统原理图Fig.3 Principle diagram of proposed control system structure for airborne platform

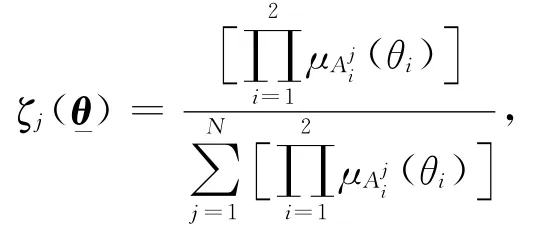
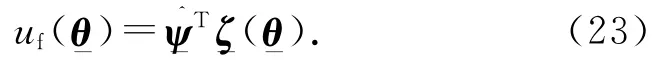
利用李雅普诺夫稳定理论来考察控制系统的稳定性.根据图3得到系统的控制律为

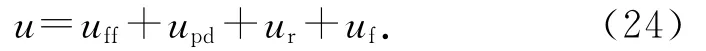
式中：uff=结合式（6），有

整理式（25），有

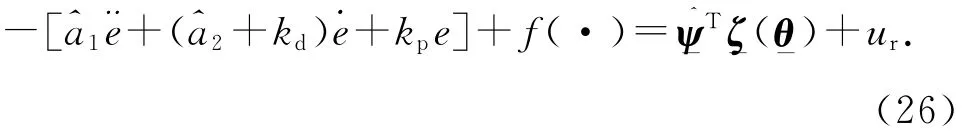
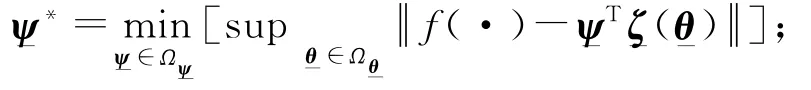
利用模糊系统逼近扰动函数f（·），有

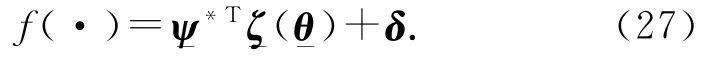
式中：Ψ-

*为参数Ψ-的最优估计值，

令

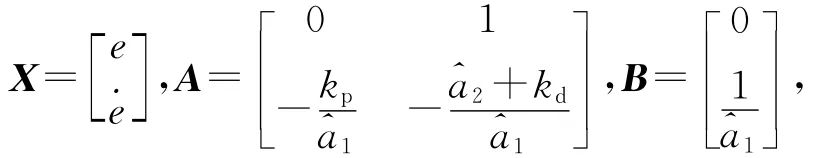
定义李雅普诺夫函数如下：

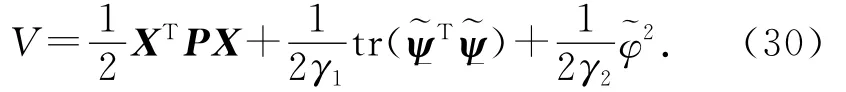
式中：γ1和γ2为学习系数，且γ1＞0，γ2＞0.将式（30）对时间进行求导：

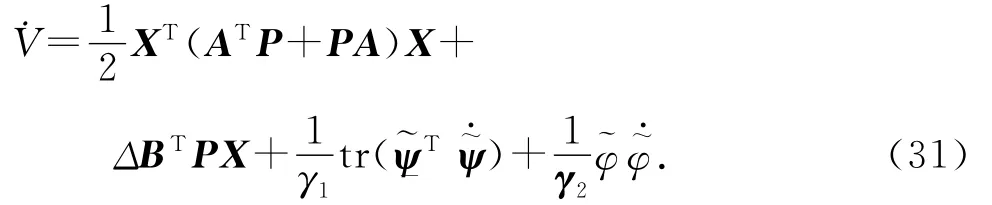
式中：ATP+PA=-Q，P、Q均为正定对称矩阵[15]，取

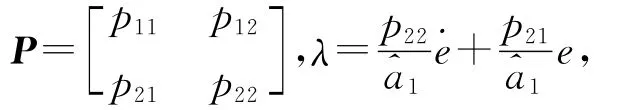
则ΔBTPX=Δλ.式（31）可以简化为

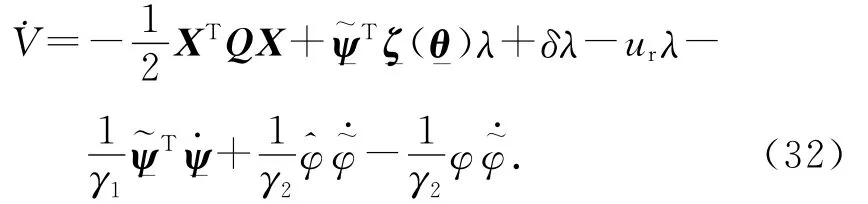
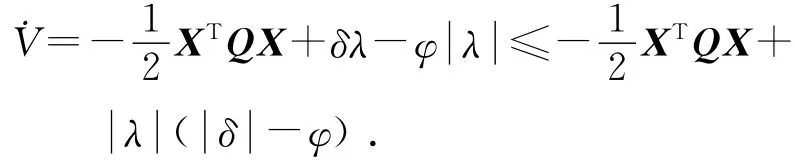
4 实验研究

该实验以搭载于某多旋翼无人机上的机载云台稳定跟踪控制系统作为研究对象，如图4所示.

系统采用TMS320F28335作为处理器，整个控制周期为30 ms，采用光电编码器作为位置传感器，测量精度是±60″.采用集成了三轴陀螺仪和三轴加速度计的某传感器作为速率传感器和加速度传感器.通过扫频法辨识得到机载云台模型的参数，激励信号为扫频信号，扫频信号重复周期T=10 s.

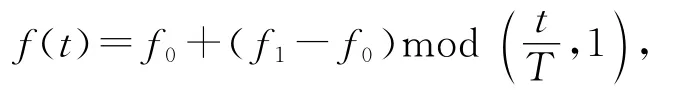
图4 实验用搭载于多旋翼无人机的机载云台Fig.4 Airborne platform mounted on multi-rotor UAV for experiment

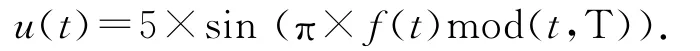
式中：f0=0，f1=10.得到的模型参数如表1所示.

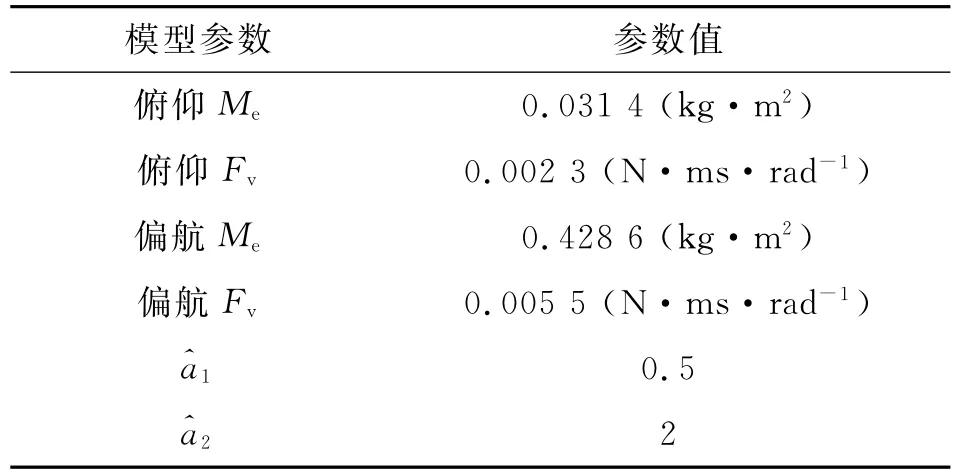
表1 机载云台模型参数Tab.1 Parameters of airborne platform system

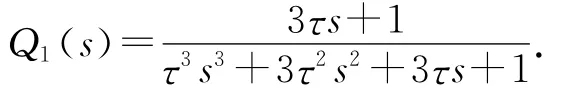
根据定理1可知，补偿控制器Q2（s）=1-P（s）× Q1（s）=1-[C（s I-A）-1B]Q1（s）.将式（5）的A、B、C代入Q2（s），可得

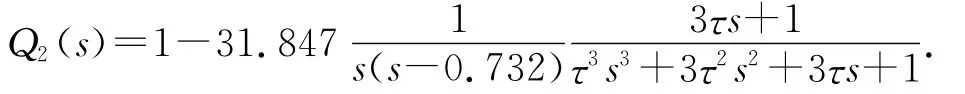
低通滤波器Q1（s）选择典型的Q31滤波器，时间常数τ=0.01，低通滤波器为

学习系数γ1=200，γ2=0.1，PD控制器参数：kp=15，kd=2，模糊控制系统模糊输入角度θ的隶属函数选取为：=exp（-（θ+1）2），= exp（-（θ+0.5）2）=exp（-（θ+0.0）2）= exp（-（θ-0.5）2=exp（-（θ-1）2）.模糊控制系统模糊输入角速度˙θ的隶属函数选取为= exp（-0.5（θ+8）2）=exp（-0.5（θ+4）2）= exp（-0.5（θ+0.0）2）=exp（-0.5（θ-4）2），μA52 =exp（-0.5（θ-8）2）.

根据图2设计的扰动观测器控制结构，以俯仰通道为例，飞行器在悬停状态下，机载云台的给定俯仰角度为0°，在两种扰动观测器结构下以100 Hz的采样频率，分别对俯仰方向上的位置传感器进行采样，获取实际的角度信息.通过维持给定角度的对比分析，验证本文提出的IVDOB控制结构抑制无人机载体扰动、维持视轴稳定的能力.如图5（a）所示为采用VDOB后视轴的角度误差曲线.图中，A为视轴角度，角度误差的最大值不超过0.8°，误差均方值小于0.25°.如图5（b）所示为采用IVDOB后视轴的角度误差曲线，误差均方值小于0.02°.本文提出的IVDOB结构相对VDOB具有更好的抑制载

对称正定矩阵体扰动的能力和更高的视轴稳定精度.

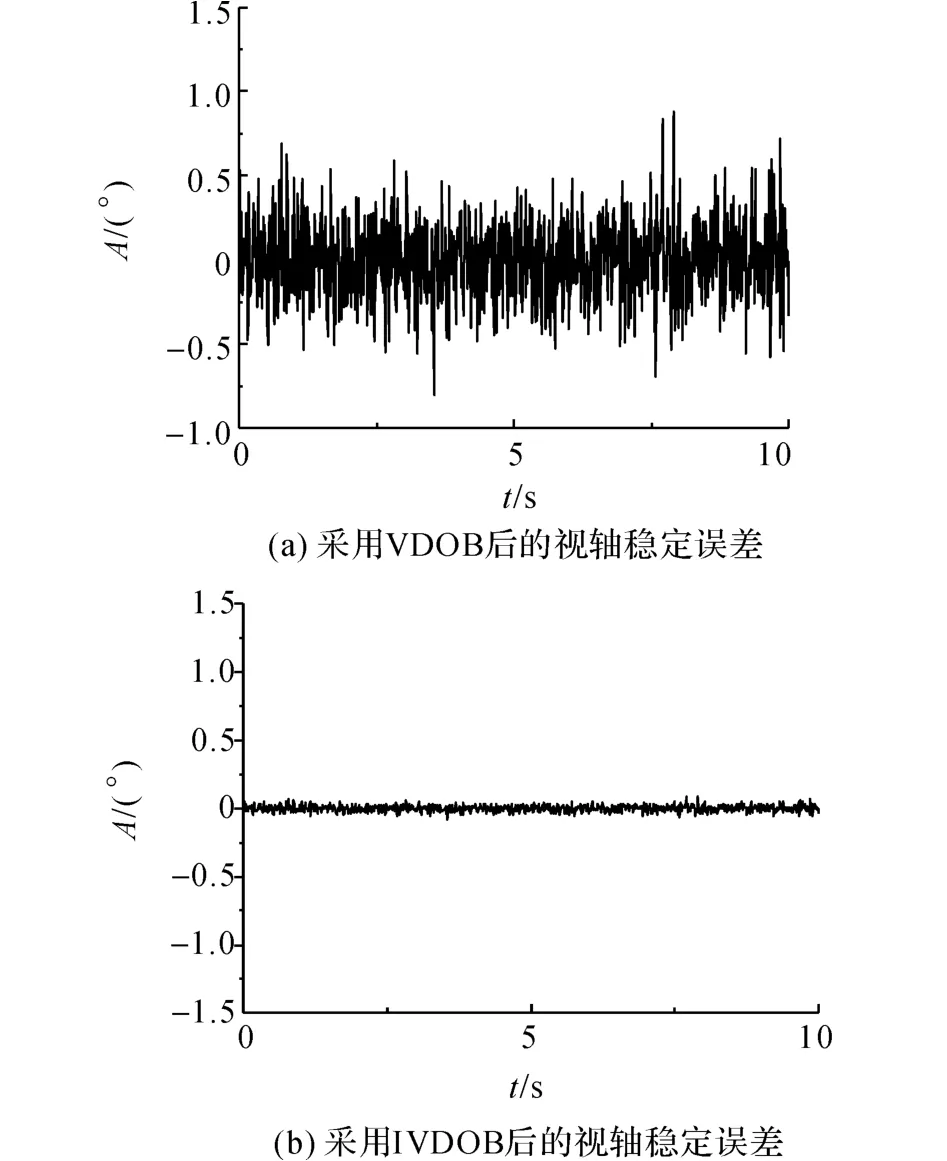
图5 视轴稳定误差对比结果Fig.5 Comparison results of line of sight error

根据图3的设计控制系统，通过本文提出的模糊自适应控制结构对给定位置信号的跟踪实验，验证该控制系统和对扰动的补偿能力.实验条件如下.在飞行过程中引入力矩扰动TD作为系统的未知扰动，如图6所示，TD通过程序加入到控制器的输出端，叠加幅值为1、信号周期为1 s的方波扰动信号Va.由于该信号与控制器没有任何信息上的交换，可以模拟实现未知干扰的引入.

如图7所示为模糊自适应控制对引入的力矩扰动TD的补偿结果.控制器的输出与扰动曲线基本一致，说明了模糊自适应控制器对力矩扰动良好的补偿能力.模糊自适应控制器输出曲线存在的振荡主要是由于IVDOB未能完全补偿机体扰动所致.

图6 引入的力矩扰动Fig.6 Introduced torque disturbance

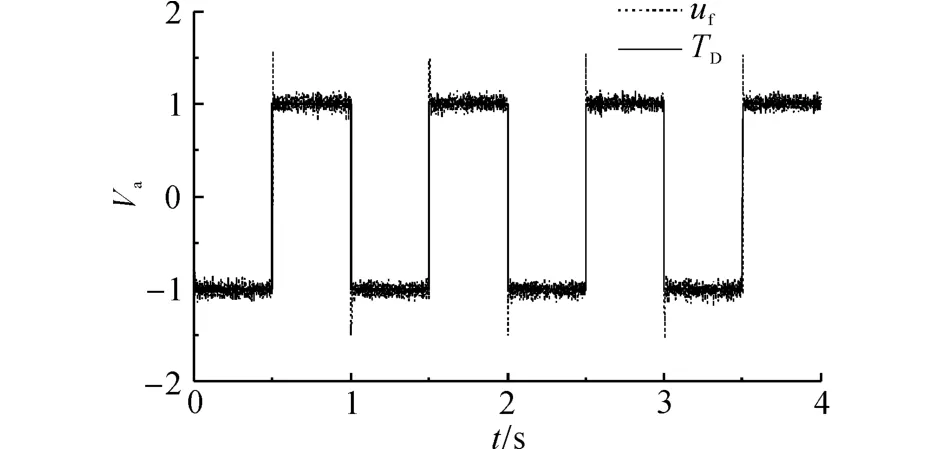
图7 模糊自适应控制器补偿TD的效果Fig.7 Result of torque disturbance rejected by fuzzy self-adjusting controller

如图8所示为未引入模糊自适应控制器的跟踪曲线及跟踪误差.可以看出，跟踪误差达到了0.2°，难以实现机载云台对给定信号的精确跟踪.如图9（a）所示为采用本文提出控制方法对正弦信号的跟踪曲线，跟踪误差的最大值不超过0.08°，且跟踪误差有界，如图9（b）所示.显然，本文提出的控制方法的跟踪效果较理想，能够精确地跟踪给定位置信号.

如图10所示为采用本文提出控制方法在外界风速约为3.2 m/s时对给定信号的跟踪效果和跟踪误差曲线.可以看出，在外界有风干扰时能够精确地跟踪给定位置信号，在给定切换点处存在的误差不超过0.8°，且基本不存在振荡.在非切换处的误差不超过0.1°.

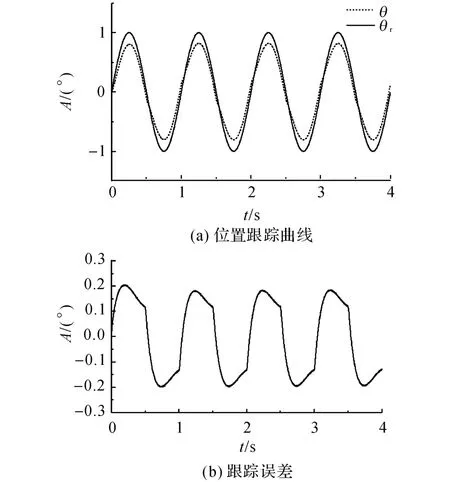
图8 未引入模糊控制器的跟踪曲线和跟踪误差Fig.8 Tracking curve and tracking error without fuzzy self-adjusting controller

图9 引入模糊自适应控制器的跟踪曲线和跟踪误差Fig.9 Tracking curve and tracking error with fuzzy self-adjusting controller

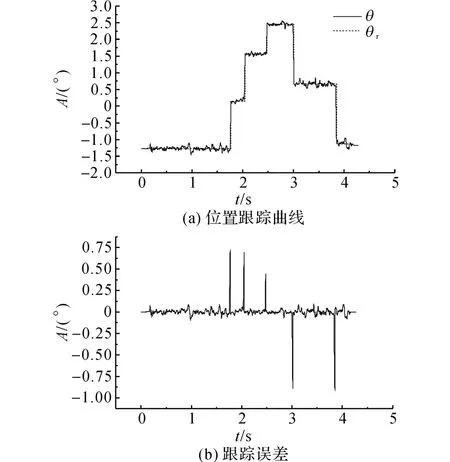
图10 在外界有风时的跟踪曲线和跟踪误差Fig.10 Tracking curve and tracking error of proposed method under wind condition

5 结 语

理论分析和机载飞行实验均表明，在扰动观测器结构中引入补偿控制器Q2后，机载云台的低频扰动和高频扰动均得到了很好的补偿，视轴稳定误差均方值小于0.02°，改进后的扰动观测器补偿扰动能力明显提高.模糊自适应控制方法能够逼近并补偿机载云台系统中的非线性未知扰动，对给定位置信号的跟踪误差小于0.08°，达到了机载云台精确跟踪的性能要求；同时，跟踪误差有界，系统渐进稳定，具有很好的稳定性和鲁棒性.综上所述，本文提出的控制方法完全满足了多旋翼无人机机载云台的稳定跟踪控制的要求.

（

）：

[1]李迪.微型飞行器电子稳像技术研究[D].长春：中国科学院长春光学精密机械与物理研究所，2012.

LI Di.Study on electronic digital image stabilization technology for the image sequences of MAV[D].Changchun：Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Science，2012.

[2]MEI Y，ZHAO H Y，GUO S Y.The analysis of Image Stabilization technology based on small-UAV airborne video[C]∥Proceedings of IEEE International Conference on Computer Science and Electronics Engineering.Hangzhou：IEEE，2012：586-589.

[3]UMENO T，KANEKO T，HORI Y.Robust servo system design with two degrees of freedom and its application to novel motion control of robot manipulators[J].IEEE Transactions on Industrial Electronics，1993，40（5）：473-485.

[4]陆建山，王昌名，何云峰，等.改进型扰动干扰器在稳定平台伺服系统中的应用[J].振动与冲击，2013，32（8）：96-99.

LU Jian-shan，WANG Chang-ming，HE Yun-feng，et al.Application of improved disturbance observer in a stable platform servo system[J].Journal of vibration and Shock，2013，32（8）：96-99.

[5]任彦，刘正华，周锐.滑模干扰观测器在低速光电跟踪系统中的应用[J].北京航空航天大学学报，2013，39（6）：835-840.

REN Yan，LIU Zheng-hua，ZHOU Rui.Application of low speed opto-electronic tracking systems based on sliding mode disturbance observer[J].Journal of Beijing University of Aeronautics and Astronautics，2013，39（6）：835-840.

[6]李嘉全，丁策，孔德杰，等.基于速度信号的扰动观测器及在光电稳定平台的应用[J].光学精密工程，2011，19（5）：998-1004.

LI Jia-quan，DING Ce，KONG De-jie，et al.Velocity based disturbance observer and its application to photoelectric stabilized platform[J].Optics and PrecisionEngineering，2011，19（5）：988-1004.

[7]谢巍，何忠亮.采用改进型扰动观测器的控制方法[J].控制理论与应用，2010，27（6）：65-700.

XIE Wei，HE Zhong-liang.Control method with improved disturbance observer[J].Control Theory and Application，2010，27（6）：695-700.

[8]高篙，徐晓霞，肖秦琨，等.机载光电跟踪系统的模糊自适应控制[J].西安工业大学学报，2009，29（6）：565-569.

GAO Song，XU Xiao-xia，XIAO Qin-kun，et al.The research on fuzzy self-adjusting control of airborne electro-optical pointing and tracking systems[J].Journal of Xi’an Technological University，2009，29（6）：565-569.

[9]朱海荣，李奇，顾菊平，等.扰动补偿的陀螺稳定平台单神经元自适应PI控制[J].电机与控制学报，2012，16（3）：65-77.

ZHU Hai-rong，LI Qi，GU Ju-ping，et al.Single-neuron adaptive PI control of the gyro-stabilized platform based on disturbance compensation[J].Electric Machines and Control，2012，16（3）：65-77.

[10]KHALIL H K.Nonlinear system[M].3rd ed.New Jersey：Prentice Hall，2002：24.

[11]HU Hong-jie，YUE Jin-yu，ZHANG Ping.A control scheme based on RBF neural network for high-precision servo system[C]∥Proceedings of IEEE International Conference on Mechatronics and Automation.Xi＇an：IEEE，2010.

[12]MILLER R，MOOTY G，HILKERT J M.Gimbal system configurations and line-of-sight control techniques for small UAV applications[C]∥Airborne Intelligence，Surveillance，Reconnaissance（ISR）Systems and Applications X，871308.Baltimore：SPIE，2013.

[13]扈宏杰，王元哲.机载光电平台的复合补偿控制方法[J].光学精密工程，2012，20（6）：1272-1281.

HU Hong-jie，WANG Yuan-zhe.Composite compensation control scheme for airborne opto-electronic platform[J].Optics and Precision Engineering，2012，20（6）：1272-1281.

[14]刘金琨.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社，2003：102-110.

[15]丁建强，任晓，卢亚平.计算机控制技术及其应用[M].北京：清华大学出版社，2012：108-120.

Fuzzy self-adjusting tracking control based on disturbance observer for airborne platform mounted on multi-rotor unmanned aerial vehicle

WANG Ri-jun1，2，BAI Yue1，XU Zhi-jun1，GONG Xun1，ZHANG Xin1，2，3，TIAN Yan-tao4

（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Science，Changchun130033，China；2.University of Chinese Academy of Science，Beijing100039，China；3.School of Electrical and Information Technology，Changchun Institute of Technology，Changchun130012，China；4.School of Telecommunication Engineering，Jilin University，Changchun130025，China）

A scheme of fuzzy self-adjusting tracking control based on an improved disturbance observer（DOB）was proposed in order to compensate disturbance and accomplish the stabilized tracking control for airborne platform mounted on multi-rotor unmanned aerial vehicle.A compensated control was introduced into feedback loop which is in the structure of original disturbance observer.An improved disturbance observer was constructed based on velocity signals.The ability of disturbance compensation and robustness were analyzed.A fuzzy self-adjusting tracking control structure was designed according to the approaching property of fuzzy system and Lyapunov stability theory.The stability of the tracking control structure was proved.The flight experiment results showed that the mean square error of line of sight was below0.02°and the error of tracking reference position was less than0.08°after applying the proposed scheme.Results demonstrate that the proposed scheme can completely satisfy the stabilized tracking control demand of airborne platform.The disturbance rejected ability was significantly improved after introducing the compensated control.The proposed control method possessed upper stabilized tracking accuracy.

multi-rotor unmanned aerial vehicle；airborne platform；disturbance observer；tracking control；fuzzy self-adjusting；stabilization

TP273

A

1008-973X（2015）10-2005-08

2014-08-26.浙江大学学报（工学版）网址：www.journals.zju.edu.cn/eng

国家自然科学基金资助项目（11372309，61304017）；院省专项资助项目（2014YSHZ004）.

王日俊（1982—），男，博士生，从事无人机载荷稳像技术的研究.ORCID：0000-0003-1576-0793.E-mail：wangrijun1982@126.com

白越，男，副研究员.E-mail：baiy@ciomp.ac.cn