基于平均驻留时间方法的牛鞭效应稳定化控制

仇 翔，宋海裕，俞 立

（1.浙江工业大学信息工程学院，浙江杭州310023；2.浙江财经大学信息学院，浙江杭州310018）

基于平均驻留时间方法的牛鞭效应稳定化控制

仇 翔1，宋海裕2，俞 立1

（1.浙江工业大学信息工程学院，浙江杭州310023；2.浙江财经大学信息学院，浙江杭州310018）

研究供应链库存系统中的牛鞭效应抑制问题.针对实际生产中订单波动补偿决策信息的可获得和不可获得2种情况，把对供应链库存系统中牛鞭效应的抑制转化为一类含有2个子系统的切换系统稳定化控制问题.采用平均驻留时间方法，给出一个充分条件，使所得的供应链库存波动切换系统指数稳定.通过求解一组线性矩阵不等式，给出订单补偿控制增益和库存波动信息权重矩阵的设计方法.通过仿真算例验证了所得的订单补偿控制策略能够有效地抑制供应链库存网络系统中的牛鞭效应.

牛鞭效应；稳定化控制；切换系统；平均驻留时间

在全球经济一体化背景下，单个企业的发展与其所在供应链中上、下游成员的发展紧密联系在一起，这迫使企业从整个供应链的角度来关注竞争力的提高.Bendiner[1]指出，有效的供应链管理方法使得企业的成本、交货率和生产周期等指标得到改善.牛鞭效应是供应链运作过程中的需求波动增大现象，它造成了供应链效率的低下，是供应链管理中的重点与难点.造成牛鞭效应的主要成因在于不能有效地获知需求波动信息.Croson等[2]从库存信息共享的角度对牛鞭效应进行分析研究.Dejonckheere 等[3]指出，在不同的库存补充策略下信息共享的效果不同，但都能够有效地降低多阶供应链中上游节点的订单波动.汪传旭等[4]指出在不同的需求自回归系数作用下，需求信息延迟会造成完全不同的牛鞭效应效果.随着不同学科交叉研究的深入，系统控制理论开始被应用到了牛鞭效应的抑制中[5-6].唐亮等[7]研究供应链系统运作中存在不确定扰动时的牛鞭效应抑制问题，设计了H∞鲁棒控制策略来减小客户不确定需求引起的生产、订货和库存波动.针对信息共享受限的情况，李翀等[8-9]运用系统稳定性理论和线性矩阵不等式方法给出库存控制策略的设计方法.针对供应链系统中存在不确定性和时滞的情形，提出鲁棒库存控制方法来抑制供应链中的牛鞭效应[10].Garcia等[11]提出一种切换控制方法来对供应链中的库存进行管理.Fu等[12]采用分散式和集中式模型预测控制方法来减小供应链系统中的牛鞭效应.

在供应链系统的实际运作中，由于库存状态信息的未及时更新、决策过程和企业之间信息交互的不及时性，订单波动补偿决策信息不一定在每个生产周期内都可获得.决策信息的不可获得，意味着牛鞭效应将不受控制.当供应链库存系统中存在决策信息不可获得的情形时，设计一个订单补偿控制策略，使牛鞭效应仍能得到抑制显得极为关键.显然地，当决策信息一直都不可获得时，牛鞭效应必定无法被抑制；因此，确定牛鞭效应可以得到控制时决策信息应满足的可获得率条件成为另一个重要问题.

在上述针对牛鞭效应的文献中，尽管给了诸多定性或定量分析，但是均忽略了决策信息的可获得率在控制策略设计中的影响.本文将订单波动补偿信息可获得和不可获得两类情况分别建模成一个切换系统中的两个子系统，从而使牛鞭效应的抑制问题转化为所得库存波动切换系统的稳定性问题.针对存在不稳定子系统的切换系统控制问题，Hespanha等[13]提出平均驻留时间概念，指出只要系统驻留在每一个子系统上的平均时间足够大，则切换系统指数稳定.近年来，平均驻留时间方法在一些网络化控制和估计问题中得到了诸多应用[14-16].本文通过引入平均驻留时间的概念，把订单补偿决策信息的可获得率转化为切换系统中子系统的平均驻留时间.通过对所得的库存波动切换系统进行稳定性分析，给出一个订单补偿控制策略的设计方法.

1 问题描述与建模

在供应链库存管理系统中，多个企业同时扮演着上游供应商和下游订货商的角色.供与求的动态变化直接影响着整个供应链系统的稳定运行.当消费需求波动超过整个供应链系统能够稳定运行的波动范围时，将会造成库存的波动，从而引发牛鞭效应.考虑一个由n个企业构成的供应链库存系统，每个企业分别以1，2，…，n进行编号.针对企业i，记Si和Ti分别为上游供应商和下游订货商的集合.在第k个生产周期中，设dli（k）为企业i发送给上游供应商l的原料订单，sli（k）为企业i从供应商l处实际收到的货物量；dij（k）为企业i从下游订货商j处收到的原料订单，sij（k）为企业i实际发给企业j的货物量.令hi（k）为企业i在第k个生产周期中由于库存短缺而未及时处理的订单量，则企业i累积的订单量有如下关系：

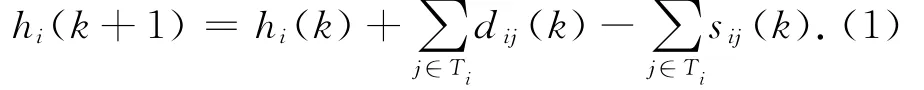
设xi（k）为企业i在第k个生产周期中的真实库存水平，则库存与收货量和发货量之间有如下关系：

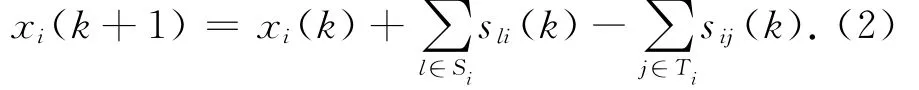
由于库存和订单总量的限制，企业i的发货量满足：

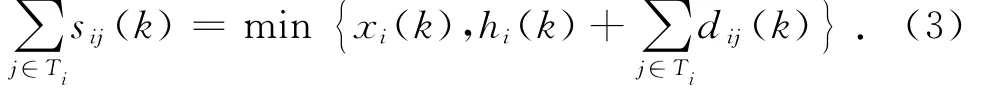
当库存量充足时，企业i的库存有如下动态平衡：

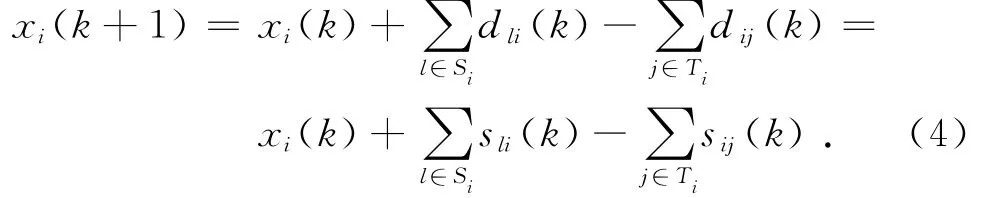
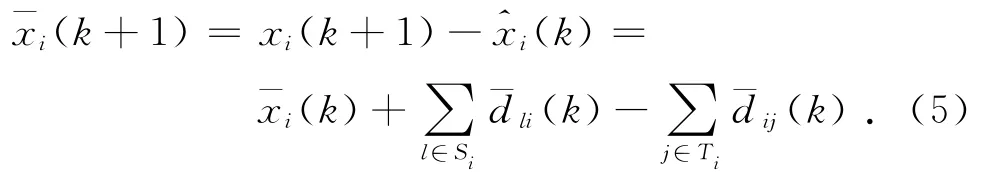
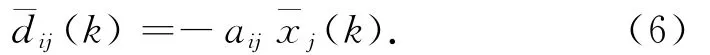
式中：aij为给定的预测比例系数.记企业因为市场需求变化而在本企业处进行的订单调整量总和为ui（k），则由式（5）、（6）可得

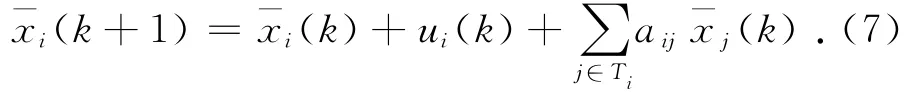
记

由式（4）可知，订单量和收货量的波动直接影响企业库存的变化.设（k）为第k个生产周期中市场需求稳定时企业i的标准库存量（k）为实际库存与标准库存的偏差，则有

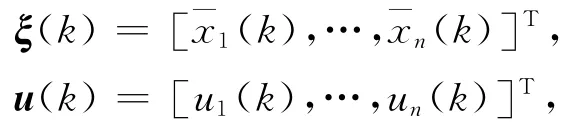
则式（7）可以改写成如下矩阵形式：

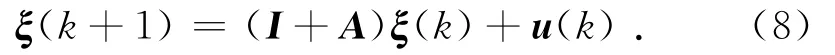
式中：A为预测比例系数矩阵，A=[aij]n×n.

从式（8）可以看出，整个供应链系统的库存波动除了受到上一生产周期库存波动的影响外，还受到上一生产周期中企业订单量变化的影响.可以通过调节各企业的订单量来抑制甚至消除牛鞭效应，即可以基于企业的库存波动信息设计合理的u（k），使得动态系统（8）趋于稳定.

结合实际情况，库存信息的获得可以由如下的输出方程描述：

式中：C为已知输出矩阵.特别地，当C为单位阵时，表示可以获得所有企业的库存信息.基于这些获得的库存信息，可以采用如下的订单补偿控制量：

式中：K为订单波动控制增益，即基于库存变化信息制定的订单调整决策系数（k）为在第k个生产周期内对供应链系统中企业库存波动水平的估计值，可由如下估计模型获得：

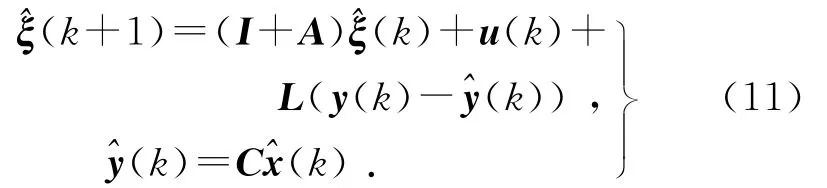
式中：L为库存波动信息权重矩阵.

在实际市场运作中，由于库存状态信息的未及时更新、决策过程和企业之间信息交互的不及时性，u（k）不一定在每个生产周期内都可获得.当第k生产周期中的订单补偿量不可获得时，则可以用前一生产周期内的控制量来进行补偿，即

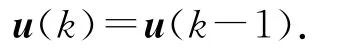
定义供应链库存波动水平的估计误差：

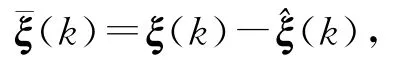
并记

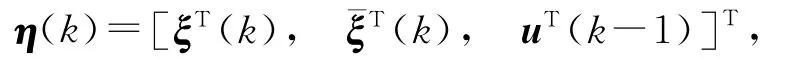
则有

1）当订单补偿决策量可获知时，整个供应链库存波动系统具有如下动态模型：

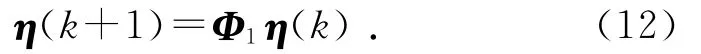
式中：

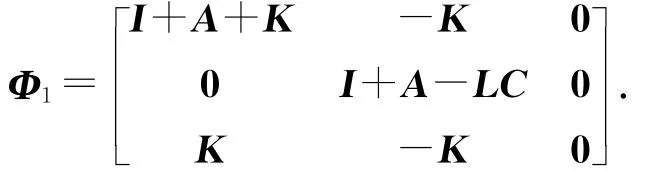
2）当订单补偿决策量不可获知时，供应链库存波动系统的动态模型为

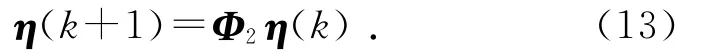
式中：

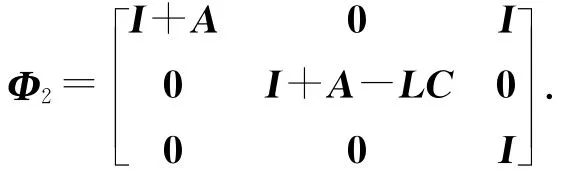
根据订单补偿决策信息是否可获得，可以将整个供应链库存波动系统看成是一个由子系统（12）和子系统（13）构成的切换系统.为此，引入一切换信号σ（k）∈{1，2}，其中σ（k）=1表示订单补偿决策信息可获得，即对应子系统（12）；σ（k）=2表示订单补偿决策信息不可获得，对应子系统（13）.式（12）、（13）可以统一写成如下切换系统模型：

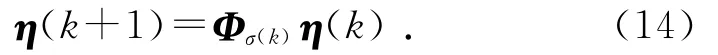
存在决策信息不可获得的供应链库存波动系统可以描述为形如式（14）的具有2个子系统的切换系统模型.对牛鞭效应的抑制问题等价转化为通过设计合理的订单补偿控制增益K和库存波动信息权重矩阵L，使得切换系统（14）稳定.为了使牛鞭效应能够以较快的速率被抑制，引入如下指数稳定的定义.

定义1考虑切换系统（14），若存在正常数c 和λ，使得对于任意给定的初始条件，系统（14）的解满足

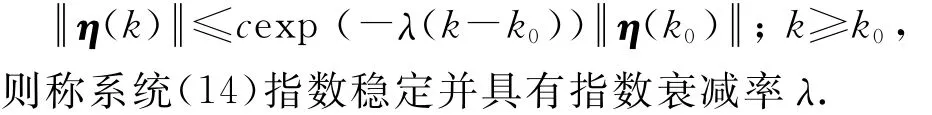
子系统（13）是一个不稳定系统，换言之，当订单补偿决策信息不可获知时，牛鞭效应会一直存在.特别地，若订货量是以扩大的形式被预测时（即矩阵A中的预测比例系数大于零），则牛鞭效应会愈演愈烈.当订单补偿决策信息可知时，则可以通过设计的K和L，使得子系统（12）稳定，从而抑制牛鞭效应直至消除.显然，即使设计好了K和L，也无法保证整个供应链库存系统可以稳定运行（特别地，若库存波动状态水平一直无法获得，则牛鞭效应将越来越严重）.因此，研究的关键在于确定订单补偿决策信息在怎样的可被获知程度下可以使系统（14）稳定.引入如下平均驻留时间的定义.

定义2［17］对于任意的τ2＞τ1＞0，令Nσ（τ1，τ2）表示切换信号σ（t）在间隔[τ1，τ2）内的切换次数.若存在τa＞0和N0≥0，使得不等式Nσ（τ1，τ2）≤N0+（τ2-τ1）/τa成立，则称τa为切换信号σ（t）的平均驻留时间，其中N0为抖动界.

不失一般性，本文取抖动界N0=0.从上面建立的模型可知，当订单补偿决策信息可获得时，切换系统（14）中的子系统1激活；当订单补偿决策信息不可获得时，子系统2激活.记每个生产周期的时间跨度为M，将k个生产周期的时间间隔[0，k M ）简记为[0，k）.记[0，k）内子系统1和2被激活的次数分别为n1和n2，则有n1+n2=k.子系统1和2的被激活率分别为r1=n1/k和r2=n2/k.本文的目标可以归结如下：设计K和L使得切换系统（14）指数稳定，同时确定订单补偿决策信息可被获得和不可被获得的最小平均驻留时间以及r1和r2应满足的条件.

2 订单补偿控制策略设计

本文基于切换系统的平均驻留时间方法，对供应链库存波动系统（14）进行稳定性分析，给出订单补偿控制器增益和库存波动信息权重矩阵的设计方法.

定理1给定库存波动系统（14）的子系统激活率r1和r2以及标量ε1、ε2和λ＞1，若存在对称正定矩阵Pi（i=1，2），使得以下线性矩阵不等式组

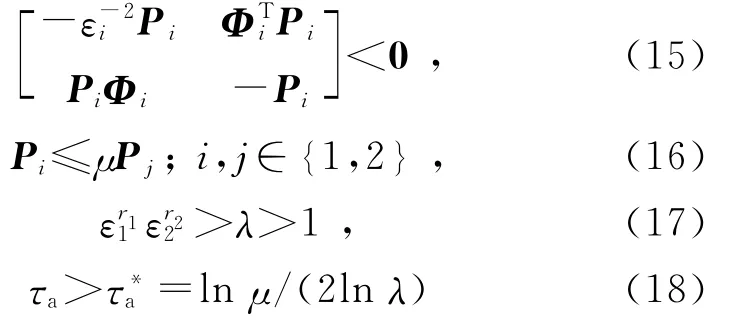
成立，则库存波动系统（14）指数稳定并具有指数衰减率λρ，其中，r1+r2=1，

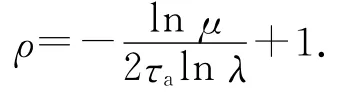
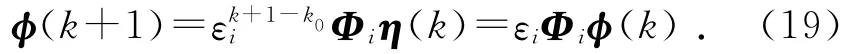
选取Lyapunov函数：

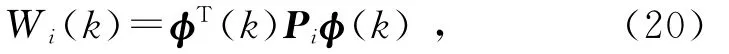
则

式中：Ωi=由条件（15）和Schur补引理可知，Ωi＜0.对于任意的φ（k）≠0，有Wi（k+1）＜Wi（k），因此，Wi（k）＜Wi（k0）.

为系统（14）选取如下Lyapunov函数：

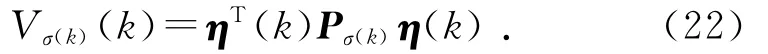
令k1，k2，…，kl为系统（14）在间隔[0，k）内的切换点，且0＜k1＜k2＜…＜kl＜k，l≥1.对于任意的子系统i∈{1，2}，有

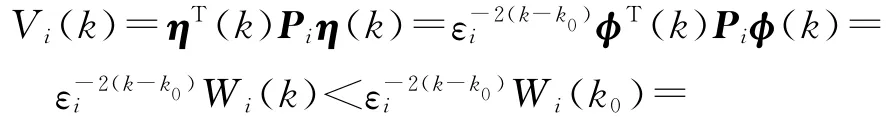
由式（23）可得

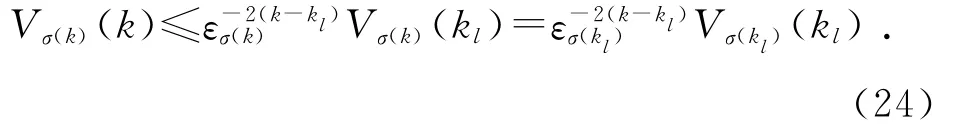
利用条件（16），有

利用式（24）和（25），可得

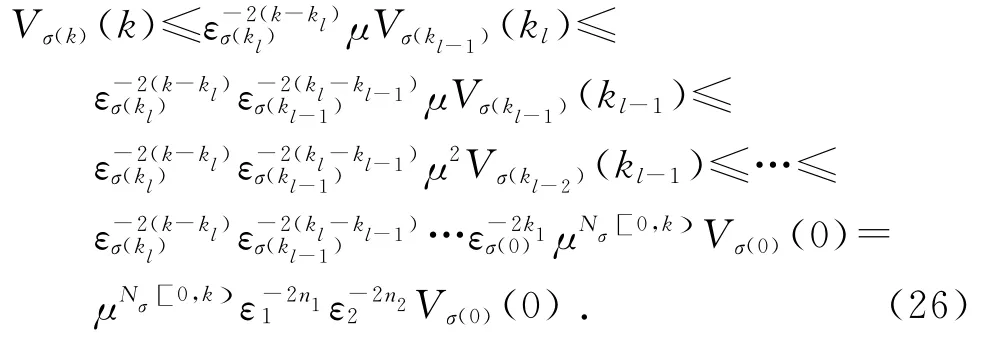
由条件（17）可知，

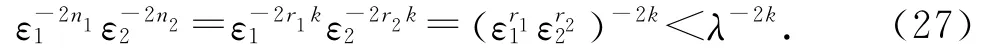
结合式（26）和（27），有

由于

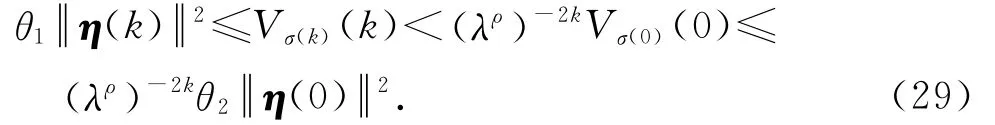
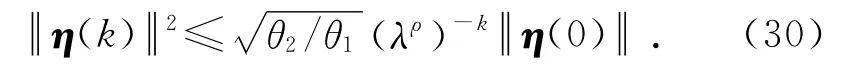
由条件（18）可知，ρ＞0.同时由λ＞1可知，λρ＞1，从而库存波动系统（14）指数稳定并具有定义1中的指数衰减率λρ.证毕.

定理1给出库存波动系统（14）具有指数稳定的订单波动补偿增益和库存波动信息权重矩阵存在性充分条件.基于该充分条件，下面将提出订单波动补偿增益和库存波动信息权重矩阵的设计方法.

定理2给定库存波动系统（14）的子系统激活率r1和r2以及标量ε1、ε2和λ＞1，若存在矩阵K、L和正定对称矩阵（i=1，2），使得以下不等式组

成立，则库存波动系统（14）指数稳定.对应的订单波动补偿增益和库存波动信息权重矩阵为K和L.同时，系统（14）的2个子系统满足的平均驻留时间为

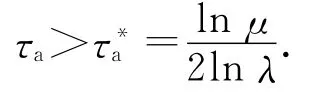
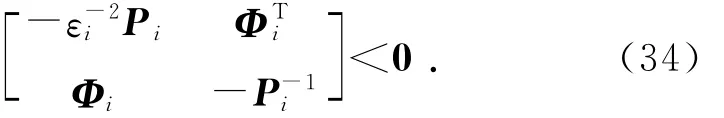
利用不等式Pi＞2I-，当

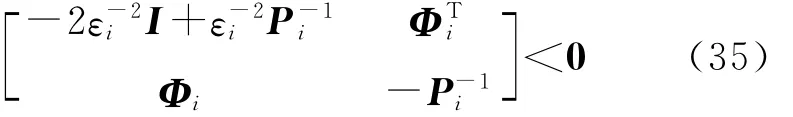
3 供应链管理系统案例仿真

某制衣有限公司为了拓展市场，在4个县级市分设了4个加工批发分部.分部之间根据各自规模可从邻近分部或总部进行货物订购，以补偿分部自身生产不足.具体的订购关系如图1所示.图中，a0j为总部对分部j的订单预测比例系数，aij为分部i对分部j的订单预测比例系数，因此，

总部和4个分部构成了一个典型的供应链库存系统，有如式（14）的库存波动方程.选取ε1=1.2和ε2=0.55，各分部对来自总部或其他分部的订单波动补偿决策信息的可获得率和不可获得率分别为r1=0.9和r2=0.1，则有=1.109 9.根据式（33）取符合条件的λ=1.1，并取μ=1.2，则可以求得应满足的最小平均驻留时间为=lnμ/（2l nλ）=0.956 5.在50个生产周期内，订单波动补偿决策信息可获得的次数为n1=50r1=45，不可获得的次数为n2=50r2=5.因此，对应的切换系统最多切换10次，即最小平均驻留时间为5，满足定理2中的平均驻留时间条件，同时系统的指数衰减率为

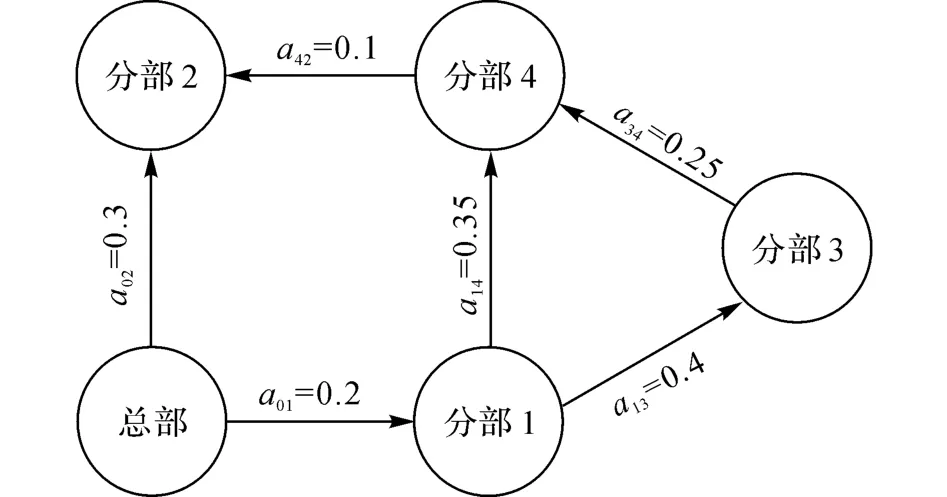
图1 订购关系图Fig.1 Figure of order relation

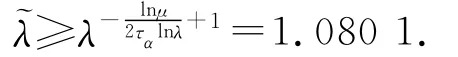
和库存波动信息权重矩阵

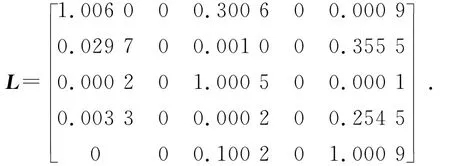
选取总部和4个分部对应的库存波动系统（14）的初始信息为

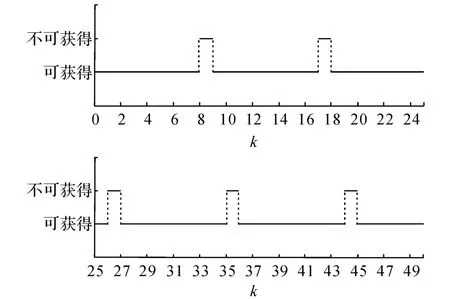
图2 订单补偿决策信息可获得和不可获得发生序列Fig.2 Occurrence sequence of available and unavailable decision information for order compensating

设各分部订单补偿决策信息的可获得和不可获得发生序列如图2所示.图中，k为生产周期.可以算得该切换序列中订单波动决策信息可获得率和不可获得率分别为90％和10％.取库存波动输出矩阵C=diag[1，0，1，0，1]，即只量测总部，分部2和分部4的库存波动状况.利用MATLAB的LMI工具箱对式（31）和（32）进行求解，可得订单波动补偿控制增益库存量的单位为百件.当订单补偿决策信息不可获得时，对应的库存波动水平轨迹如图3所示.可以看出，由于订单一直无法受到补偿调整，随着生产的进行，总部和各分部的牛鞭效应愈演愈烈.当订单补偿决策信息具有90％的获得率时，对应的库存波动水平轨迹如图4所示.图中，Tr为库存.可以看出，根据定理2的设计方法得到的订单波动补偿控制策略很好地抑制了该制衣有限公司供应链系统中的牛鞭效应.对比图3和4可以发现，尽管订单补偿决策信息不能一直被获得，但是如果获得率得到保证，则可以有效地抑制牛鞭效应.通过仿真结果的对比分析可以看出，当供应链库存管理系统中决策信息无法一直获得时，本文所给的订单补偿控制策略可以有效地抑制牛鞭效应.

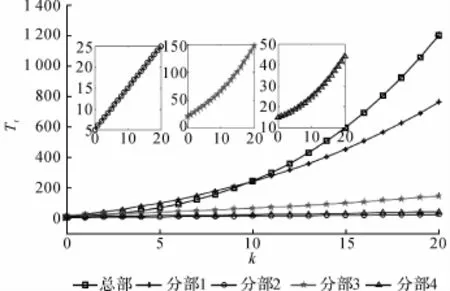
图3 订单补偿决策信息不可获得时的库存波动轨迹图Fig.3 Trajectories of inventory when decision information for order compensating is unavailable

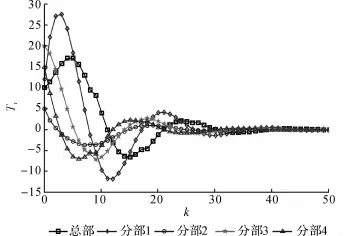
图4 订单补偿决策信息获得率为90％时的库存波动轨迹图Fig.4 Trajectories of inventory when available rate of decision information for order compensating is 90％

4 结 语

在供应链库存管理系统中，由于库存状态的未及时更新、决策过程和企业之间信息交互的不及时性，使得订单波动决策信息无法在每个生产周期内都能被获得.通过对订单补偿控制信息的可获得和不可获得2种情况进行分别建模，本文将供应链库存系统中的牛鞭效应抑制问题转化为了一类含有2个子系统的切换系统稳定化控制问题.基于平均驻留时间方法，通过求解一组线性矩阵不等式给出订单补偿控制增益和库存波动信息权重矩阵的设计方法.仿真结果表明：当订单补偿决策信息不可获得时，企业的牛鞭效应会愈演愈烈；当订单补偿决策信息的可获得率得到保证时，则可以通过所设计的订单补偿控制方法有效地抑制牛鞭效应.在供应链实际运作中，企业之间的交互信息会存在不确定性，同时库存调度过程中会受到时间滞后的影响.因此，进一步的研究可以考虑具有信息交互不确定性和调度时延的供应链牛鞭效应抑制问题.

（

）：

[1]BENDINER J.Understanding supply chain optimization [J].APICS-The Performance Advantage，1998，1：34-40.

[2]CROSON R，DONOHUE K.Behavioral causes of the bullwhip effect and the observed value of inventory information[J].Management Science，2006，52（3）：323-336.

[3]DEJONCKHEERE J，DISNEY S M，LAMBRECHT M R，et al.The impact of information enrichment on the bullwhip effect in supply chains：a control engineering perspective[J].European Journal of Operational Research，2004，153（3）：727-750.

[4]汪传旭，崔建新.ARMA（1，1）需求条件下需求信息延迟对两级供应链牛鞭效应和平均成本的影响[J].系统管理学报，2007，16（3）：332-336.

WANG Chuan-xu，CUI Jian-xin.Impact of demand information delay on order variation and average cost in a two-stage supply chain with ARMA（1，1）demand[J].Journal of Systems and Management，2007，16（3）：332-336.

[5]BAGANHA M，COHEN M.The stabilizing effect on inventory in supply chains[J].Operational Research，1998，46（3）：572-583.

[6]黄小原，卢震.供应链牛鞭效应的H∞控制应用研究[J].控制与决策，2002，18（2）：155-158.

HUANG Xiao-yuan，LU Zhen.Application of H∞control strategies of bullwhip effect in supply chain[J].Control and Decision，2002，18（2）：155-158.

[7]唐亮，靖可.H∞鲁棒控制下动态供应链系统牛鞭效应优化[J].系统工程理论与实践，2012，32（1）：155-163.TANG Liang，JING Ke.Bullwhip effect optimization of dynamic supply chain system based on H∞robust control[J].Systems Engineering：Theory and Practice，2012，32（1）：155-163.

[8]李翀，刘思峰.信息共享受限条件下的供应链网络系统牛鞭效应控制策略[J].控制与决策，2012，27（12）：1787-1792.

LI Chong，LIU Si-feng.Bullwhip effect control strategy in supply chain networks with limited information sharing [J].Control and Decision，2012，27（12）：1787-1792.

[9]LI C.Controlling the bullwhip effect in a supply chain system with constrained information flows[J].Applied Mathematical Modeling，2013，37（4）：1897-1909.

[10]LI C，LIU S F.A robust optimization approach to reduce the bullwhip effect of supply chains with vendor order placement lead time delays in an uncertain environment[J].Applied Mathematical Modeling，2013，37（3）：707-718.

[11]GARCIA C，IBEAS A，VILANOVA R.A switched control strategy for inventory control of the supply chain[J].Journal of Process Control，2013，23（6）：868-880.

[12]FU D，IONESCU C，AGHEZZAF E，et al.Decentralized and centralized model predictive control to reduce the bullwhip effect in supply chain management[J].Computers and Industrial Engineering，2014，73：21-31.

[13]HESPANHA J，MORSE A.Stability of switched systems with average dwell time[C]∥Proceeding of the 38th IEEE Conference on Decision and Control.Phoenix：IEEE，1999：2655-2660.

[14]ZHANG W，YU L.Output feedback stabilization of networked control systems with packet dropouts[J].IEEE Transactions on Automatic Control，2007，52（9）：1705-1710.

[15]ZHANG L，BOUKAS E K，SHI P.Exponential H∞filtering for uncertain discrete-time switched linear systems with average dwell-time：aμdependent approach [J].International Journal of Robust and Nonlinear Control，2008，18（11）：1188-1207.

[16]ZHAO X，ZHANG L，SHI P，et al.Stability of switched positive linear systems with average dwell time switching[J].Automatica，2012，48（6）：1132-1137.

[17]ZHAI G S，HU B，YASUDA K，et al.Qualitative analysis of discrete-time switched systems[C]∥Proceeding of the2002 American Control Conference.Anchorage：IEEE，2002：1880-1885.

Bullwhip effect control based on average dwell time method

QIU Xiang1，SONG Hai-yu2，YU Li1

（1.College of Information Engineering，Zhejiang University of Technology，Hangzhou 310023，China；2.College of Information，Zhejiang University of Finance and Economics，Hangzhou 310018，China）

The bullwhip effect control problem was analyzed for the supply chain system.Considering the fact that the decision information for order compensating may be lost or not，the bullwhip effect control problem of the supply chain systems was converted to a stabilization problem of a class of switched systems with two subsystems.A sufficient condition was provided by using the average dwell time method in order to ensure that the supply chain inventory system is exponentially stable.The order compensation controller and the weighted matrix of the inventory fluctuation were designed by solving a set of linear matrix inequalities.An illustrative example was provided to demonstrate the effectiveness of the proposed order compensation control strategy in controlling the bullwhip effect for supply chain systems.

bullwhip effect；stability control；switched system；average dwell time

TP273

A

1008-973X（2015）10-1909-07

2014-11-03.浙江大学学报（工学版）网址：www.journals.zju.edu.cn/eng

国家自然科学基金资助项目（61273117）.

仇翔（1980—），男，讲师，博士生，从事先进控制理论、供应链优化技术等的研究.ORCID：0000-0001-9925-856X.

E-mail：qiuxiang@zjut.edu.cn