基于分层Dirichlet过程的频谱利用聚类和预测

刘阳阳戴明威黄晓霞

1(中国科学院深圳先进技术研究院 深圳 518055)

2(中国科学院大学 北京 100049)

基于分层Dirichlet过程的频谱利用聚类和预测

刘阳阳1，2戴明威1，2黄晓霞1

1(中国科学院深圳先进技术研究院 深圳 518055)

2(中国科学院大学 北京 100049)

认知无线电网络通过动态频谱接入技术,利用授权频段的空闲时段实现频谱共享。对频谱利用特征的描述和未来利用率的预测有利于实现高效频谱感知算法,进而优化频谱接入策略。通过对标准的分层Dirichlet过程进行扩展,提出了一种跨信道的非参数贝叶斯模型UTD-HDP(UTD扩展的分层Dirichlet过程),用于无线频谱利用率数据的聚类分析和分布参数估计。利用该模型,可以自适应地描述无线频谱利用率的特征,实现了对未来时间频谱利用率的高精度预测。

频谱利用特征提取;频谱利用预测;分层Dirichlet过程;Ginns采样

1 引 言

无线频谱是一种有限、宝贵的自然资源,国际通信联盟(International Telecommunication Union)定义可用的无线频谱上限为3000 GHz。为防止不同设备的相互干扰,当前无线网络采用固定的频谱分配政策:由政府部门根据不同无线电业务的技术特点、业务能力、带宽需求等因素划分不同的频段。随着通信技术的不断发展,各种无线应用如广播、电视、移动通信等不断涌现,无线频谱资源将被耗尽已成为业界的共识。

调查发现,无线频谱各频段利用率介于15%～85%,而且不同频段频谱利用率在不同时间和地域呈现出很强的波动性[1]。为解决无线频谱资源耗尽的问题,提高无线频谱利用率,研究人员提出了认知无线电网络的概念[2,3]。认知无线电网络采用动态频谱接入技术,利用授权频谱的空闲时段进行通信,实现频谱共享,从而提高频谱利用率。在认知无线电网络系统中,非授权用户可以感知授权信道的频谱占用状态,然后利用授权信道的空闲时隙进行通信,并且在授权用户需要通信时退出授权信道。

检测授权频谱利用率的动态变化需要精确的频谱感知技术和快速的频谱转换策略。这对于实时变化的频谱利用来说难度极大,无法实现。因此通过对授权用户使用无线频谱资源的模型和规律进行挖掘,实现频谱利用率的预测,对设计高效的频谱感知算法和频谱接入策略具有十分重要的意义。目前,频谱预测技术主要有两类:信号强度预测和信道占用状态预测[4]。对于信道的信号强度预测,主要有基于自回归滑动平均模型(AutoregressiveMovingAverageModel,ARMA)[5,6]、自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)[7]进行回归分析的方法,以及结合了经验模态分解(Empirical Mode Decomposition,EMD)的支持向量回归(Support Vector Regression,SVR)方法;而对于信道占用状态的预测,主要有基于马尔科夫链[8,9],隐马尔科夫模型[9]以及频繁模式挖掘[4,10]等方法。以上方法均能达到一定的预测精度。

ARMA、SVR回归分析和基于马尔科夫链的方法只能对单个信道的利用率或占用状态进行回归分析和建模预测。考虑到信道间的相关性,本文采取了一种基于分层Dirichlet过程的无限混合模型,将一组信道的利用率数据表示为一组无限混合的概率分布模型。这是一种非参数贝叶斯模型,模型中的参数个数不是固定的,而是自适应地随着数据变化[11,12]。通过应用分层Dirichlet过程,在统一的模型中对多个不同信道的利用率数据进行建模,可以将一组信道的利用率数据聚类为不同的模式,实现跨信道的模式类共享,从而实现鲁棒性更好的建模和预测。特别是在数据稀疏的情况下进行建模预测时,可以结合其他信道的数据减小数据缺失对预测精度的影响。

2 分层 Dirichlet 过程混合模型

分层Dirichlet过程是Dirichlet过程在随机分布上的层次泛化,本文简要介绍这两种模型及其在数据聚类中的应用。

2.1 Dirichlet过程混合模型

Dirichlet过程是一种随机过程。1973年, Ferguson[13]提出其定义:假设G0是测度空间上的随机概率分布,参数α是正实数,如果空间上的概率分布G满足对的任意一个有限划分A1,A2,…,Ar,均有,则G服从由基分布G0和参数α确定的Dirichlet过程[11],记为

令X={x1,x2,…,xn}为观测数据的集合, Dirichlet过程混合模型可以将观测数据xi聚类,每类由一个概率密度函数f(θi)表示。Dirichlet过程混合模型可以用如下的生成式模型表示:

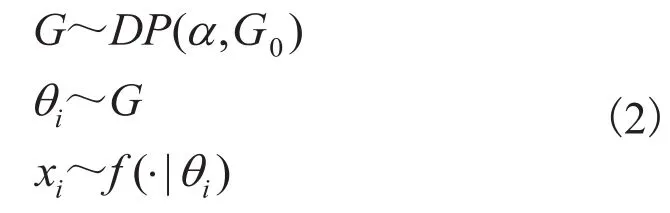
其中,G为关于θi的先验分布,服从Dirichlet过程;为Concentration参数;G0为基分布;θi为聚类的类参数,用以描述每个类的概率分布f(θi)。基分布G0可以连续分布或离散分布,而DP(α,G0)以概率1将先验分布G0离散化,从而使得观测数据可以形成聚类[14],这是一个无限混合模型。与K-means等聚类方法不同,类参数θi的个数不是指定的,而是与观测数据xi的个数相等。若两个数据的类参数相等,即θi=θj,则xi和xj隶属于同一类。

2.2 分层 Dirichlet 过程混合模型

Dirichlet过程混合模型可以对单组数据进行聚类分析和分布参数估计,但是无法描述多组数据间共享聚类的特性。非参数贝叶斯模型分层Dirichlet过程(Hierarchical Dirichlet Process, HDP)[11,12]混合模型的提出,为多组数据间共享聚类问题提供了解决方法。

令X1,X2,…,XJ表示J组数据,其中Xj={xj1,xj2,…,xjnj}。与Dirichlet过程混合模型相似,分层 Dirichlet过程混合模型对每组数据分别定义了一个概率分布Gj,作为每组数据中每个观测数据xji对应类参数θji的先验分布。为在多组数据间共享聚类,使。其中,G0为全局概率分布,满足;为 Concentration参数;H为基分布。这是一个两层的分层Dirichlet过程,其生成式模型表示为:

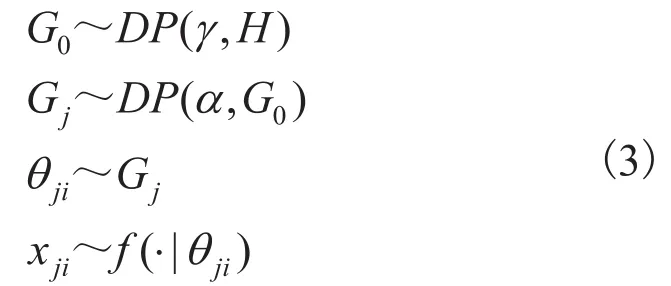
其中,xji表示第j组数据中第i个数据;θji为jji对应的类参数。

注意到基分布H本身也可以定义为服从Dirichlet过程,因此分层Dirichlet过程可以根据需要继续扩展分层。分层Dirichlet过程混合模型的参数推断主要有变分推断和马尔科夫链蒙特卡罗(Markov Chain Monte Carlo,MCMC)采样方法两种。Teh[11]给出了分层Dirichlet过程在中国连锁餐馆过程(Chinese Restaurant Franchise,CRF)框架下的三种Ginns采样算法,分别为基于CRF的后验采样算法,增强表示的后验采样算法和直接分配后验采样算法。

3 分层 Dirichlet 过程在频谱利用率数据分析中的应用

本文使用基于分层 Dirichlet过程混合模型的非参数贝叶斯模型来对频谱利用率数据进行聚类分析和预测。无线频谱可以细分为多个信道,本文将一组信道记为,每个信道的频谱利用率数据为一个连续的时间序列,记为。其中,表示信道Cj在ti时刻的频谱利用率。标准的分层Dirichlet过程混合模型无法描述含有时间变量的观测数据。McInerney等[15]通过对标准分层 Dirichlet过程混合模型进行扩展,提出LocHDP模型,用于描述含有时间变量的人群地点观测数据。借鉴LocHDP的扩展方法,本文给出了针对信道频谱利用率数据进行建模分析扩展的分层Dirichlet过程模型,称为UTD-HDP模型。

3.1 UTD-HDP模型

频谱利用率的高低主要取决于相应服务的使用程度,频谱利用率的变化与人们日常生活习惯息息相关。令,其中,表示一周中的周一至周日;tji表示一天中的时间;该三元组表示信道Cj一周中dji这天tji时刻的频谱利用率为uji。UTD-HDP模型的基本思想就是挖掘频谱利用率数据变化的模式,建立非参数贝叶斯模型,并进行预测。令θji表示xji对应的模式类,一个观测数据的概率分布可以表示为几个模式类不同概率的混合,其似然度为:

在分层Dirichlet过程混合模型中,进行多组数据分析的关键在于类参数的共享,例如在文档主题分析中,词汇表在主题间是共享的。而在频谱利用率分析中,不同信道可能在某些时间表现出某种模式,但不同信道在相同模式下对应的利用率可能也不同,例如广播电视信号,不同信道可能在某个相同的时间点呈现不同的利用率模式。因此,对于频谱利用率数据不同文档的不同模式间共享时间变量即tji和dji,利用率变量uji则和相应信道Cj相关。具体地来说,利用率uji为连续变量,使用高斯分布来描述其概率分布,如下:

为使时间分布平滑并且表示缺失时间的分布情况,同样使用高斯分布来估计时间变量tji的概率分布,如下:

时间变量dji是离散的,使用多项分布来描述:

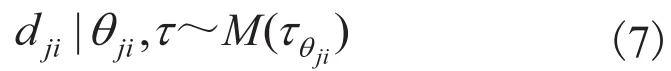
在分层Dirichlet过程混合模型中,为计算方便,式(5)(6)(7)中的分布参数均取相应的共扼先验分布[16,17],如式(8)所示:

其中, 为Normal Inverse-Gamma分布;a、b和c均为超参数。

将该扩展的分层Dirichlet过程混合模型记为UTD-HDP,其生成式过程如下所示:

(1)从一个Dirichlet过程中采样全局概率分布G0,根据G0生成全局模式类的分布:

(2)对每个全局模式类 ,生成共享变量t和d相关的类参数:

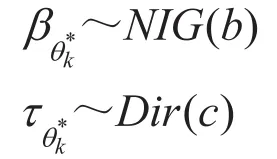
(3)对每个信道Cj,以G0为基分布,生成该信道中模式类的概率分布:

(4)对信道Cj中每个模式类θji,生成每个信道的利用率变量u相关的模式类参数:

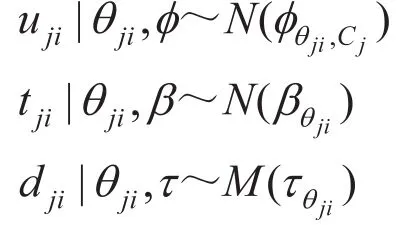
3.2 参数推断

Teh等[11]给出了分层Dirichlet过程混合模型在中国连锁餐馆(CRF)框架下的三种Ginns采样算法。在CRF框架中,每个观测数据xji被看作一个顾客,每组数据则被视为一个餐馆。对于每个顾客,首先被分配到一个餐桌,每个餐桌被分配一道菜,通过将顾客分配到不同的餐桌,每个餐桌分配菜来对顾客进行聚类,分配到相同菜的顾客,也就是数据,即隶属于同一类。

本文扩展了其中直接分配后验采样算法,直接将每个数据分配给特定类,分配餐桌的过程由每组数据中每一类的餐桌数目mjk体现。每次采样主要对五个变量进行采样,分别为每个数据所属类θji,每组数据中每一类的餐桌数目mjk和类的全局概率分布φk,以及超参数α和γ。对于UTD-HDP模型,变量mjk和φk以及超参数α和γ的采样过程与标准HDP模型相同,这里不再赘述。下面给出θji的采样方法。

根据UTD-HDP模型定义,对于数据xji,已知分配给类k的其他数据时,xji隶属于类k,即θjk=k的条件概率为:

将式(5)(6)(7)以及式(8)表示的参数共扼先验分布代入式(9)各项,积分消参,可得

根据Teh等[11]研究结果,采样公式为

图1给出了UTD-HDP模型进行参数推断的Ginns采样算法。首先进行初始化,对各个训练数据随机分配模式类,并计算对应模型参数,初始化完成后进行Ginns采样。实际应用发现,进行100次迭代,算法即可收敛。

图1 UTD-HDP模型的Gibbs采样算法Fig.1 Gibbs sampling algorithm for UTD-HDP

3.3 利用率预测

对所观测的样本进行Ginns采样后,即可得到UTD-HDP模型的参数。根据该模型,可以预测未来某时刻各信道的频谱利用率。

具体地,指定未来一个时刻,即一周中的日期变量d和这天中的时间变量t,根据3.1节定义的模型,UTD-HDP可以给出该时刻的利用率在[0,1]区间上的连续概率分布,从而得到该时刻的利用率预测值。对于某个信道Cj,该概率分布如下:

其中,X为观测数据集合;表示根据X建立的UTD-HDP模型的参数集合;θ为分配的模式类;为利用率;d,t均为时间变量。

由贝叶斯定理,式(13)中,

因此,(13)式化简为

其中,S表示共进行S次采样,上式表示取S次采样的平均分布;角标中的s表示第s次采样得到的不同参数。

4 实验与结果分析

在深圳市取三个地点:中国科学院深圳先进技术研究院科研楼、深圳市宝安区某居民楼和深圳市南山区科技园某办公楼,从2013年8月1日至2013年12月1日进行历时四个月的频谱测量工作。使用能量探测法测量了315 M、433 M(对讲机及遥控频段)、470 M(数字电视频段)、CDMA、GSM以及2.4G等六个频段的各信道接收信号强度(Received Signal Strength Indication,RSSI)数据。本文以GSM下行频段测量数据为例进行实验分析。该频段测量频率范围为948.9 MHz～959.7 MHz,测量分辨率为0.4 MHz,分为25个信道,每秒钟扫描一次。对每个信道的接收信号强度数据,根据经验值设置频谱占用的阈值,得到每秒钟的占用状态,并根据占用周期得到每段时间的利用率水平。本文取其中20个信道从2013年10月15日0:00至2013年11月4日23:59共三周数据进行分析。取前两周每半个小时的利用率数据作为训练集,建立UTD-HDP模型,并根据该模型预测第三周的频谱利用率,同观测值进行比较,分析预测精确度。

4.1 频谱利用率聚类

选取适当的超参数,利用图1算法对训练数据集进行聚类分析,共发现8个模式类。图2为一周中不同模式类的天概率分布,结果显示不同的模式类在一周中出现概率各不相同。图3为各个模式类在一天中不同时刻的概率密度,直方图为该模式类中数据的概率分布。从图3可以看出在各个模式类中,时间变量数据符合所对应的高斯分布,且不同模式类发生的时间各不相同。各模式类中利用率变量的分布同各信道相关,图4展示了第5个模式类在第10至第18共9个信道利用率的概率密度。观察可知,各信道中各个模式类中数据符合所对应的高斯分布,并且不同信道的同一模式类的参数各不相同。图5展示了各个模式类在第1至第9共9个信道的概率分布,可以看出不同信道中各个模式类的分布各异。综上可以看出,所得结果符合UTD-HDP模型信道间共享时间变量,利用率变量局限于每个信道的定义,并且各个模式类在信道间实现共享,达到了建模目标。

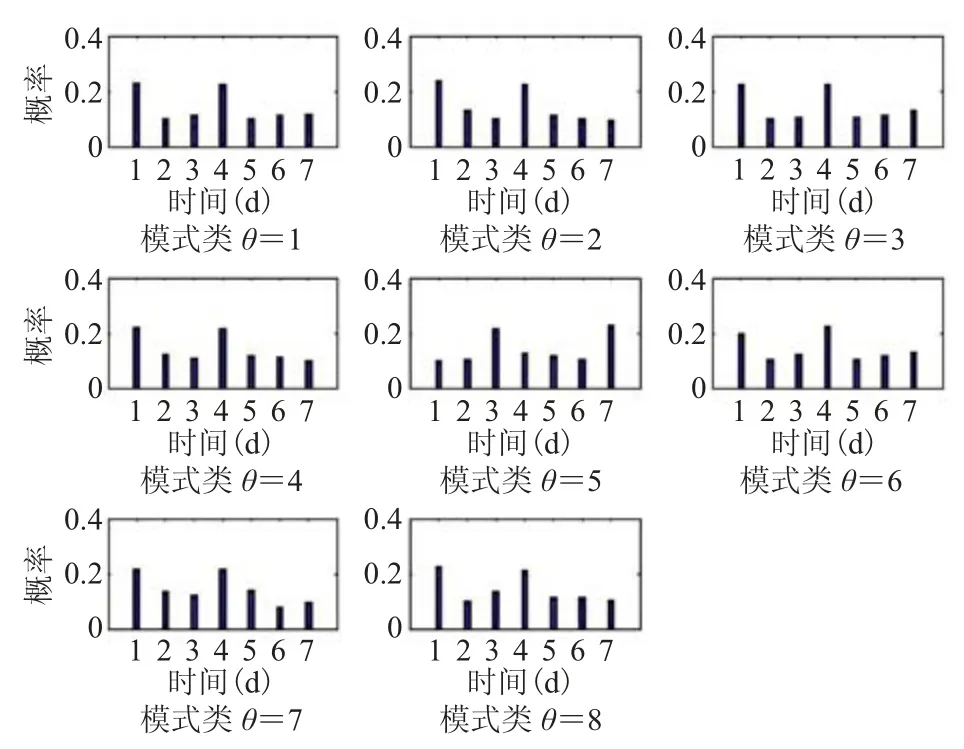
图2 各个模式类在一周时间d的概率分布Fig.2 Probability distribution of days for each pattern

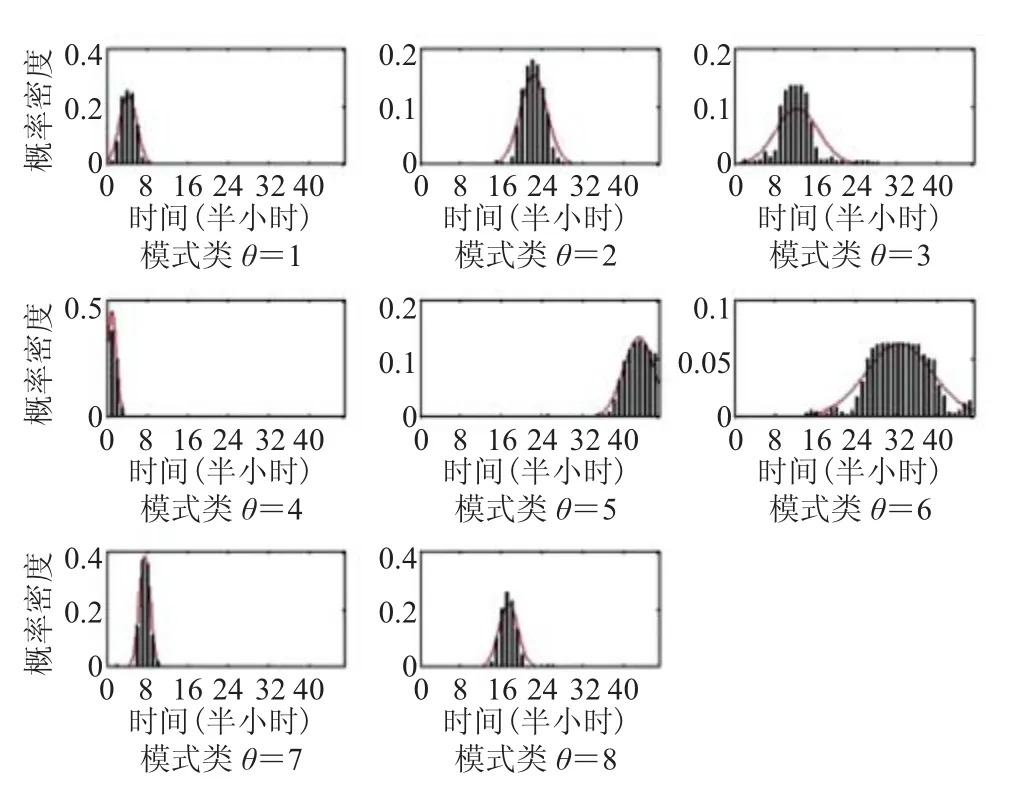
图3 各个模式类的时间t概率分布Fig.3 Probability distribution of time for each pattern

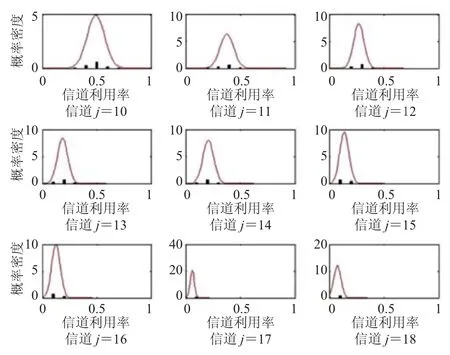
图4 第5个模式类在信道10～18中利用率u的概率分布Fig.4 Probability distribution of utilization for pattern 5 in channel 10-18

图5 各个模式类在信道1～9的概率分布Fig.5 Probability distribution of patterns in channel 1-9

4.2 频谱利用率预测

利用3.3节预测算法和通过前两周数据建立UTD-HDP模型对这20个信道在第三周的频谱利用率进行预测。图6展示了对第5、第7和第12共3个信道的预测结果。图6显示该算法对测试集中一周的频谱利用率预测结果精度很高,平均平方误差的平均值为0.0036。表1展示了这3个信道预测结果平均平方误差(MSE)。

其中,N为测试数据个数;ui为观测值; 为预测值。

为进行对比,采用Wang等[7]的ARIMA时间序列方法预测结果作为对比。注意到训练集中这两周即2013年10月15日至2013年10月28日的测量数据缺失比较严重,每个信道实际应为672个数据,实际观测数据平均为430个,数据缺失率达到36%。为建立ARIMA模型,对缺失数据进行了周期平滑化处理。对每个信道,选取季节性乘法ARIMA模型进行回归预测,通过AIC(Akaike Information Criterion)准则确定模型阶数,然后对第三周的频谱利用率进行预测。第5、第7和第12这3个信道的预测结果见图7。从图7可以看出,与UTD-HDP模型预测结果相比,ARIMA模型的预测结果精度略有不足。表1为分别利用UTD-HDP模型和ARIMA时间序列模型进行预测(图6和图7)的3个信道的平均平方误差,及20个信道的平均平方误差的平均值。对比可知,与经过周期平滑处理后的ARIMA模型预测结果相比,UTD-HDP模型的利用率预测平均平方误差都有明显减小,三个信道分别减少8.33%、73.3%和14.56%,20个信道的平均值减小了23.4%。UTD-HDP模型预测精度明显更高。因此,UTD-HDP模型进行预测时,通过跨信道的模式共享,其他信道的信息可以弥补某些信道数据缺失的影响,即可以有效解决数据稀疏的问题。

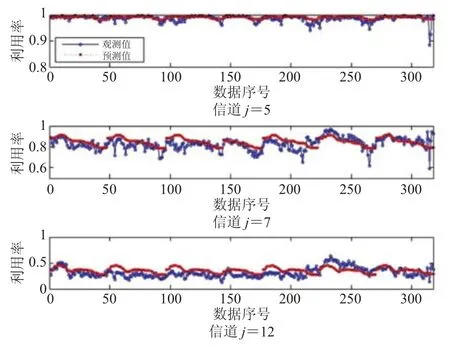
图6 UTD-HDP模型的预测结果Fig.6 Prediction result using UTD-HDP

图7 ARIMA模型的预测结果Fig.7 Prediction result usingARIMA

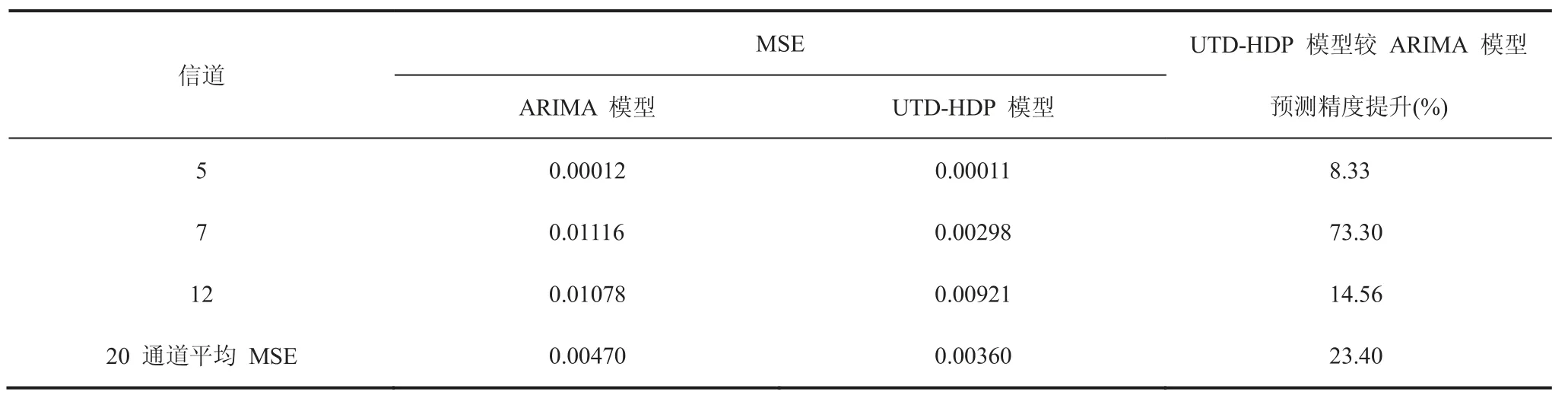
表1 两种模型预测结果的平均平方误差对比结果Table 1 Comparison result of MSE of prediction using ARIMA and UTD-HDP

5 结论和展望

在本文中,我们针对频谱利用率在时间、频率维度的相关性,对标准HDP模型进行扩展,提出了跨信道的多元信道利用率数据进行建模分析的UTD-HDP模型。该模型可以对多个信道的频谱利用率时间序列进行聚类分析,挖掘信道利用率的模式类,并根据所建立的模型进行利用率预测,并且达到较高的预测精度。

在未来工作中,一方面是进行进一步的实验,考察分析不同信道数目以及时间长度对于聚类和预测精度的影响。另一方面,UTD-HDP模型的一个缺陷是需要调节参数,不同参数对模式类聚类以及预测精度都有明显影响,在图1算法中添加超参数采样过程以解决这一问题。

[1] Federal Communicaitons Commission.Notice of proposed rule making and order(FCC 03-222) [DB/OL].[2014-08-04].http://wen.cs.ucdavis. edu/～liu/289I/Material/FCC-03-322A1.pdf.

[2] Mitola J,Jr Maguire GQ.Cognitive radio:making software radios more personal[J].IEEE Personal Communications,1999,6(4):13-18.

[3] Akyildiz IF,Lee WY,Vuran MC,et al.Next generation/dynamic spectrum access/cognitive radio wireless networks:a survey[J].Computer Networks,2006,50(13):2127-2159.

[4] Huang P,Liu CJ,Li X,et al.Wireless spectrum occupancy prediction nased on partial periodic pattern mining[C]//IEEE 20th International Symposium on Modeling,Analysis&Simulation of Computer and Telecommunication Systems,2012: 51-58.

[5] Wen ZG,Luo T,Xiang WD,et al.Autoregressive spectrum hole prediction model for cognitive radio systems[C]//IEEE International Conference on Communications Workshops,2008:154-157.

[6] Su JZ,Wu W.Wireless spectrum prediction model nased on time series analysis method [C]//Proceedings of the 2009 ACM Workshop on Cognitive Radio Networks,2009:61-66.

[7] Wang Z,Salous S.Spectrum occupancy statistics and time series models for cognitive radio[J]. Journal of Signal Processing Systems,2011,62(2): 145-155.

[8] Ghosh C,Corderiro C,Agrawal DP,et al.Markov chain existence and hidden Markov models in spectrum sensing[C]//IEEE International Conference on Pervasive Computing and Communications,2009:1-6.

[9] Song CQ,Chen DW,Zhang Q.Understand the predictanility of wireless spectrum:a large-scale empirical study[C]//2010 IEEE International Conference on Communications,2010:1-5.

[10]Yin SX,Chen DW,Zhang Q,et al.Mining spectrum usage data:a large-scale spectrum measurement study[J].IEEE Transactions on Monile Computing,2012,11(6):1033-1046.

[11]Teh YW,Jordan MI,Beal MJ,et al.Hierarchical Dirichlet processes[J].Journal of the American Statistical Association,2006,101(476):1566-1581.

[12]Teh YW,Jordan MI,Beal MJ,et al.Sharing clusters among related groups:Hierarchical Dirichlet processes[C]//Advances in Neural Information Processing Systems,2005:1385-1392.

[13]Ferguson TS.A nayesian analysis of some nonparametric pronlems[J].The Annals of Statistics,1973,1(2):209-230.

[14]Jnandi S,Woolrich MW,Behrens TEJ.Multiplesunjects connectivity-nased parcellation using hierarchical Dirichlet process mixture models[J]. NeuroImage,2009,44(2):373-384.

[15]Mclnerney J,Zheng J,Rogers A,et al.Modelling heterogeneous location hanits in human populations for location prediction under data sparsity[C]// Proceedings of the 2013 ACM International Joint Conference on Pervasive and Uniquitous Computing,2013:469-478.

[16]Bishop CM.Pattern Recognition and Machine Learning[M].New York:Springer,2006.

[17]Murphy KP.Conjugate Bayesian Analysis of the Gaussian Distrinution[Z].2007.

Spectrum Utilization Clustering and Prediction Based on Hierarchical Dirichlet Process

LIU Yangyang1,2DAI Mingwei1,2HUANG Xiaoxia1

1(Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences,Shenzhen518055,China)
2(University of Chinese Academy of Sciences,Beijing100049,China)

Cognitive radio networks achieve spectrum sharing ny utilizing the idle periods of licensed nands via dynamic spectrum access technique. Spectrum characterization and prediction help perform more efficient spectrum sensing and then optimize spectrum access strategy. In the paper, UTD-HDP, a nonparametric Bayesian model, was introduced ny extending the standard HDP(Hierarchical Dirichlet Process) to perform utilization data clustering and distrinution parameters estimation. Using this model, we characterized the features of spectrum utilization adaptively and predicted the future spectrum utilization with high accuracy.

spectrum utilization feature extraction； spectrum utilization prediction； hierarchical Dirichlet process； Ginns sampling

TN 92

A

2014-04-04

:2014-08-04

刘阳阳(通讯作者),硕士研究生,研究方向为认知无线电网络,E-mail:liu.yy@siat.ac.cn;戴明威,硕士研究生,研究方向为认知无线电网络;黄晓霞,博士,研究员,博士生导师,研究方向为无线传感网络、认知无线电网络、无线通信和移动计算。