基于空间几何结构的特征跟踪算法
2015-01-07樊春玲赵永刚冯良炳
樊春玲 赵永刚 邓 亮 冯良炳
(中国科学院深圳先进技术研究院 深圳 518055)
基于空间几何结构的特征跟踪算法
樊春玲 赵永刚 邓 亮 冯良炳
(中国科学院深圳先进技术研究院 深圳 518055)
针对传统的基于标记的增强现实系统场景受限等缺点,提出一种基于特征空间几何结构的无标记跟踪算法。在传统的金字塔Kanade-Lucas-Tomasi(KLT)跟踪算法基础上,通过建立图像的多尺度空间模型并在多尺度空间模型中对图像进行实时跟踪,同时根据图像特征间特有的空间几何结构信息优选跟踪特征点,解决了在多尺度变化情况下视频图像特征跟踪稳定性问题。实验结果表明,提出的跟踪算法在给定的数据库上性能高效稳定,与同类跟踪算法相比跟踪精度大幅提高,每帧重投影错误率均小于1像素,保持在亚像素级别。
空间几何;自然特征;增强现实;跟踪
1 引 言
增强现实技术(Augmented Reality)是在虚拟现实技术的基础上发展起来的新技术,通过计算机系统将虚拟模型叠加到真实场景中,增强用户感官体验,从而实现对现实的增强。该技术已逐渐被应用到军事、辅助医疗诊断与培训、教育与娱乐等众多领域。
目前很多增强现实系统是基于事先准备好的标记来获取相机与物体的位置关系。基于标记的增强现实系统中一个典型的代表就是华盛顿大学发布的软件开发包ARToolKit[1],它使用事先准备好的矩形标记并将其特征存储在数据库中,当摄像机捕捉到包含标记的场景时检测并识别标记,再根据已知的世界坐标和摄像机内参标定出得到摄像机的姿态。在这之后,各种不同类型的标记如Artag等[2,3]也被广泛研究。然而这种基于标记的增强现实系统在实际应用中必须事先准备标记,并将标记存储于数据库中,因此其应用场景存在较大局限性。
近年来,随着计算机视觉技术和计算机图形学技术的迅速发展,无标记的自然物体跟踪增强现实系统已成为发展趋势。无标记增强现实系统可以通过对图像进行自然特征提取并通过对运动过程中自然特征的跟踪来掌握相机的姿态,因此可以在任何场所和时间即时使用增强现实技术。要掌握好相机和物体位置关系,首要条件就是对图像的自然特征进行检测并在运动过程中准确地跟踪特征。
学者们在自然特征检测和跟踪方面做了大量的研究也取得了一定的成效[4,5]。Lowe[6]提出的缩放不变特征转换算子(Scale-Invariant Feature Transform,SIFT)是一种对图像旋转、缩放等保持不变性的图像局部特征,但其计算太复杂,不能满足增强现实系统的实时要求。Hernert等[7,8]在SIFT思想的基础上提出了一种快速鲁棒的角点特征,该特征基于积分图像和盒子滤波的简化实现,其运算速度比SIFT快得多。Rostenw等[9]提出了加速分割检测特征角点,对于灰度图像,检测候选特征点周围一圈的像素值,如果该点周围邻域内有足够多的像素点与该点的灰度值差别足够大,则认为该候选点为一个特征点。该方法简单快速,能够达到实时检测要求,如并行跟踪和定位[10,11],但是对旋转和亮度变化敏感。基于特征的跟踪方法中,主要有光流跟踪Kanade-Lucas-Tomas(KLT)算法以及后来在其基础上扩展的金字塔KLT[12]算法。传统金字塔KLT方法中采用金字塔图像利用较小的窗口跟踪较大运动变化的特征,首先在金字塔最顶层(最模糊层)搜索特征点得到本层的光流,然后将其作为下一层(较清晰层)光流的初始估计值,再计算下一层的光流,直到最底层(最清晰层)。该方法对平移变化的图像有良好的跟踪效果,但在具有尺度变化的特征跟踪效果需进一步改进。
本文在传统金字塔KLT跟踪算法基础上,提出一种基于图像自然特征空间几何结构的多尺度跟踪方法,对金字塔KLT方法的改进体现在:(1)在图像的多尺度空间模型上同时进行特征点跟踪和融合;(2)利用特征点的空间几何结构信息进行优化。基于这两点改进,解决多尺度变化对象的跟踪稳定性问题。
2 算法描述
本文提出的基于图像自然特征空间几何结构的无标记跟踪方法,算法流程如图1所示。

图1 算法流程图Fig.1 Algorithm flow chart
首先对视频第一帧图像角点特征进行检测;接着分别为后续每帧图像建立一个多尺度空间模型,并在图像多尺度空间模型中的每一层图像上跟踪第一帧检测到的特征点,然后将每层跟踪到的特征点融合并剔除异常点,即可得到每帧图像的跟踪点;再通过随机抽样一致性算法(Random Sample Consensus,RANSAC)对每帧跟踪特征点所在平面与第一帧图像所在平面求取单应性矩阵,根据单应性矩阵将第一帧检测到的特征点映射到每帧图像上得到映射点;最后根据每帧图像上的映射点和跟踪点的空间几何特征筛选特征点。
2.1 特征提取
与金字塔KLT算法相同,本文也采用Shi-Tomasi[14]角点进行特征检测和跟踪。Shi-Tomasi角点在传统Harris角点的基础上进行改进,其定义的基础为图像灰度强度的二阶导数矩阵——二维的Hessian矩阵:

根据Shi-Tomasi定义,若矩阵H的两个特征值中较小的一个大于设定的阈值,则认为该点是较强的特征点。
2.2 特征跟踪
(1)建立多尺度空间模型
由于传统的金字塔KLT算法对多尺度变化的视频跟踪效果不稳定,因此本文算法首先为需跟踪的每帧图像建立多尺度空间模型,然后在每层图像上对特征进行跟踪,能够实现对多尺度变化的视频稳定跟踪。采用带有低通滤波的下采样方法对每帧图像建立具备不同分辨率的图像多尺度空间模型。自上向下,将原图像按照不同的尺度系数缩放为不同大小的图像,多尺度空间模型的层数可根据视频内容目标变化程度设定。
(2)多尺度空间搜索
对首帧图像中检测到的特征点,在图像的每层空间图像上采用金字塔KLT跟踪方法进行特征点跟踪。使用金字塔KLT方法时,假设有一个包含特征信息的窗口w,所有像素点(x,y)都向一个方向移动了(vx,vy),从而得到( ),即t时刻的(x,y)点在t+τ时刻为(x+vx,y+vy),所以寻求匹配的问题可化为最小化式(2),式中,wx和wy分别为窗口在x和y方向上的半径。对于灰度图,A(x,y)为t时刻的图像中点(x,y)处的亮度值,B(x+vx,y+vy)为t+τ时刻的图像中点(x+vx,y+vy)的亮度值。
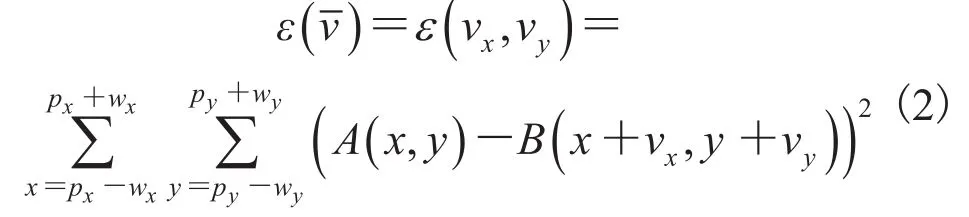
对首帧图像的特征点序列在后续帧的每个尺度空间图像进行搜索。本文采用5层的尺度模型空间,最后得到5组新的特征点序列,称为不同尺度空间的特征点序列。
在图像多尺度空间模型中每层图像上跟踪特征点的结果不尽相同。在一些层上部分特征点会丢失,并且每帧的丢失情况各异,因此在多尺度空间模型中对每层图像搜索可以弥补由于尺度变化等造成的特征点丢失。
(3)多尺度特征点融合
每层上的特征点序列仅代表该层尺度空间的跟踪效果,要得到每帧的特征点序列,需要将不同尺度的特征点序列根据其空间几何结构一一对应来进行融合。本文逐点对比每层空间特征点跟踪结果,对比其在每层的跟踪误差值,选取三层空间中跟踪误差最小的点作为该帧最终的跟踪点,其坐标根据式(3)计算得出:

其中,vi为i点的最终跟踪坐标;分别表示在第vi第l层上跟踪到的点的x和y方向坐标;scalel是第l层的尺度系数。图2给出了三层空间模型的示意图。第一层中跟踪到的特征点为(1,3,4,6,8),第二层中跟踪到的特征点为(1, 2,3,4,6,7,8),第三层中跟踪到的特征点为(1,2, 3,5,7,8)。融合过程具体为对比跟踪到的特征点的误差值,将误差较小的作为最终跟踪到的点,最终得到本帧的跟踪点为(1,2,3,4,5,6,7,8)。对于三层中均未跟踪到的少数点认为其丢失。

图2 多尺度空间特征点融合Fig.2 Feature points blending in multi-scale model
(4)剔除异常点
同所有测量数据一样,跟踪也会因计算及其他原因造成误差。本文对每帧跟踪特征点序列中误差较大的点进行剔除操作,通过设置合适的“置信域”,位于“置信域”范围外的点认为是异常点,如图3中(a)为前一帧跟踪到的特征点,(n)为后一帧跟踪到的特征点。其中,虚线圈代表按照其他跟踪点变化规律在本帧应该出现的位置,红色点为与其他点变化相比变化异常的特征点。异常值判断的准则中最常用的误差处理方法是准则,表达式见式(4):

其中,xd为映射点和对应跟踪点的欧氏距离;为所有点对应距离的平均值;为标准方差。
先计算首帧跟踪特征点序列和每帧跟踪点序列的变化情况,即距离,其中m为跟踪到的点个数,再根据 准则结合测量数据点较少的实际情况,将“置信域”设置为,位于“置信域”之外点将被剔除。
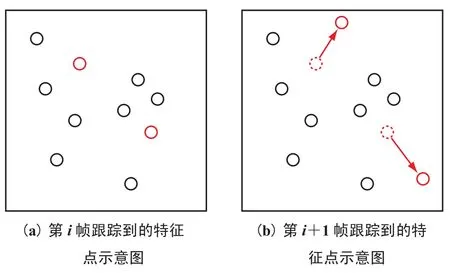
图3 相邻帧跟踪示意图Fig.3 Tracking results in sequence
2.3 优化特征点
(1)求取单应性矩阵
在计算机视觉中,平面的单应性是从一个平面到另一个平面的投影映射。本文利用RANSAC方法从第一帧检测的特征点和后续每帧跟踪到的特征点中分别选择四对以上特征点,求取第一帧图像所在平面和后续每一帧图像所在平面的单应性矩阵H,见式(5):

其中,u为首帧检测到的特征点;v为后续某一帧跟踪到的特征点。特征点坐标均采用齐次坐标形式。
(2)映射特征点
通过单应变换将首帧特征点序列映射到当前帧图像中得到映射点序列,这些映射点序列将作为候选特征点。
(3)优化特征点
在跟踪过程中,由于目标位置变化剧烈等原因导致跟踪失败的情况有两种:一种是跟踪点丢失,另一种是跟踪点位置错误。针对这两种情况,本文算法提出了相应的处理措施:①对于跟踪中丢失的特征点,根据当前帧上其余跟踪良好的点得到该帧所在平面与首帧所在平面的单应变换关系,再由此单应变换关系将第一帧中与此点对应的特征点映射到当前帧上,得到一个新的特征点。对这个新的特征点根据式(1)求取H矩阵,判断其较小的特征向量是否大于设定阈值,如果大于阈值则将该点加入特征点序列。②根据与映射点之间的欧式距离剔除跟踪错误的特征点。跟踪点如果与其相应映射点的距离较大(大于设置的阈值),则认为该点是异常点,应在每帧特征点序列中剔除掉该点。最终,通过上述步骤得到每帧图像中跟踪到的首帧特征点序列的跟踪点序列。
3 实验及结果分析
本方案已在处理器为AMD AthlonTMII X2 B24 2.99 GHz,操作系统为Microsoft Windows XP的计算机上实现,为检测算法的跟踪效果,采用Metaio标准库[15]测试本文提出的算法在不同尺度变化情况下跟踪的准确度,结果见图4。其中,图4(a)为对“CAR”图像缩放至0.25倍跟踪效果对比,图4(n)为缩放至0.4倍跟踪效果对比,且在图4(a)和(n)中,左图均为采用金字塔KLT方法跟踪效果,右图均为采用本文算法跟踪效果。从图4可看出,在不同的尺度上跟踪中,本文算法跟踪到的特征点数目以及准确性明显优于传统金字塔KLT算法。

图4 本文方法和金字塔KLT方法跟踪不同尺度变化的图像对比图Fig.4 Tracking result for using proposed method and KLT
图5 显示Metaio标准库中“STOP”组图的跟踪效果,图中绿色线条表示跟踪成功的特征。图5(a)为对原始图像缩小至0.25倍跟踪效果,图 5(n)为将原始图像顺时针旋转 30°跟踪效果,图5(c)为将原始图像顺时针旋转60°跟踪效果。从图5中可看出,本文算法不但对多尺度变换跟踪稳定,并且对旋转保持稳定性。
图6与图7分别显示采用金字塔KLT、带方向性的加速分割检测特征和旋转不变的二进制鲁棒独立基本特征(Oriented FAST and Rotated BRIEF,ORB)[16]以及本文算法对两段视频(分别为300帧和600帧,分辨率均为1280×720像素)做跟踪的每帧重投影错误率。结合图6和图7可看出,本文算法每帧重投影错误率均小于1像素,而金字塔KLT算法和ORB算法重投影错误率相对较大而且在对部分帧的跟踪中出现较大波动,并且由于本文算法中对跟踪的特征点进行了基于空间几何特征信息的优化,包括跟踪错误点的剔除和跟踪丢失点的找回,重投影错误率没有出现较大波动的情况,因此跟踪性能稳定。实验表明,本文算法与金字塔KLT、ORB算法相比,对于多尺度变化的对象跟踪准确性和稳定性均有大幅提高。

图5 本文方法对Metaio数据库“STOP”图跟踪效果Fig.5 Feature points tracked results from Metaio“STOP”

图6 金字塔KLT、ORB与本文算法跟踪结果(视频1)Fig.6 Results of tracking via Pyramidal KLT,ORB and our method(video 1)

图7 传统金字塔KLT、ORB与本文算法跟踪结果(视频2)Fig.7 Results of tracking via Pyramidal KLT,ORB and our method(video 2)
4 结束语
本文提出一种可用于无标记增强现实系统的跟踪算法。通过对真实场景中目标图像的自然特征进行检测,建立图像的多尺度模型并在模型中的每层图像上跟踪特征点;同时,根据特征点的空间几何结构对多尺度特征点进行融合;最后通过RANSAC方法求取单应性矩阵并映射特征点,对比映射点和跟踪点之间的空间几何关系优化跟踪点。实验结果表明,本文算法应用于无标记增强现实系统中时,在图像的多尺度空间模型中进行特征点搜索方法更适用于具有多尺度变化的视频跟踪,并能得到实时准确的跟踪效果。
[1] Kato H,Billinghurst M.Marker tracking and HMD calinration for a video-nased augmented reality conferencing system[C]//Proceedings of the 2nd IEEE and ACM International Workshop on Augmented Reality,1999:85-94.
[2] Bergamasco F,Alnarelli A,Rodola E,et al.RUNETag:a high accuracy fiducial marker with strong occlusion resilience[C]//IEEE Conference on Computer Vision and Pattern Recognition,2011: 113-120.
[3] Uchiyama H,Saito H.Random dot markers[C]// IEEE Virtual Reality Conference,2011:35-38.
[4] Uchiyama H,Marchand E.Onject detection and pose tracking for augmented reality:Recent approaches[C]//The 18th Korea-Japan Joint Workshop on Frontiers of Computer Vision,2012.
[5] Van Krevelen DWF,Poelman R.A survey of augmented reality technologies,applications and limitations[J].International Journal of Virtual Reality,2010,9(2):1-20.
[6] Lowe DG.Distinctive image features from scaleinvariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[7] Bay H,Tuytelaars T,Gool LV.SURF:speeded up ronust features[C]//Proceedings of the 9th European Conference on Computer Vision,Lecture Notes in Computer Science,2006,3951:404-417.
[8] 张志禹,刘耀阳.基于SURF与光流法的增强现实跟踪注册[J].计算机工程与应用,2013,doi: 10.3778/j.issn.1002-8331.1303-0339.
[9] Rosten E,Drummond T.Machine learning for highspeed corner detection[C]//Proceedings of the 9th European Conference on Computer Vision,Lecture Notes in Computer Science,2006,3951:430-443.
[10]Klein G,Murray D.Parallel tracking and mapping for small AR workspaces[C]//The 6th IEEE and ACM International Symposium on Mixed and Augmented Reality,2007:225-234.
[11]Klein G,Murray D.Parallel tracking and mapping on a camera phone[C]//The 8th IEEE International Symposium on Mixed and Augmented Reality,2009:83-86.
[12]Bouguet JY.Pyramidal implementation of the affine lucas kanade feature tracker description of the algorithm[OL].[2014-07-03].http://ronots. stanford.edu/cs223n04/algo_affine_tracking.pdf.
[13]Fischler MA,Bolles RC.Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J].Communications of the ACM, 1981,24(6):381-395.
[14]Shi J,Tomasi C.Good features to track[C]// Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition,1994: 593-600.
[15]Runlee E,Ranaud V,Konolige K,et al.ORB:an efficient alternative to SIFT or SURF[C]//IEEE International Conference on Computer Vision, 2011:2564-2571.
[16]Academic Research and Punlications[OL].[2014-07-03].http://www.metaio.com/research/.
Feature Tracking Based on Space Geometry Structure
FAN Chunling ZHAO Yonggang DENG Liang FENG Liangning
(Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences,Shenzhen518055,China)
In this paper, a novel method for tracking without a marker was proposed. This method alleviated many constraints in augmented reality systems nased on fiducial markers. To improve the tracking stanility in multi-scale, the effective features and space geometry structure were detected, and the effective features were searched in a multi-scale model. Based on space geometry structure of features, the effective feature points were selected and fictitious features points were wiped off. Experiments show that the proposed algorithm works ronustly in the video with scaling onjects. The feature points reprojection error of every frame is smaller than one pixel, and the average of feature points reprojection error is kept in sun-pixel.
space geometry; natural feature; augmented reality; tracking
TP 391.41
A
2013-12-30
:2014-07-04
国家自然科学基金项目(61070147);深圳市科技研发资金基础研究计划(JC201105190951A,JC201005270331A)
樊春玲,硕士,研究方向为图像处理、增强现实等;赵永刚,硕士,研究方向为增强现实,图像处理等;邓亮,硕士,研究方向为模式识别、视频监控等;冯良炳(通讯作者),博士,研究方向为智能计算与智能控制、多视角三维重建及增强现实等,E-mail:ln.feng@siat.ac.cn。
