一种基于圆的几何特性改进的圆检测随机算法

舒龙庆 曾垂力

(四川大学计算机学院 成都 610065)

一种基于圆的几何特性改进的圆检测随机算法

舒龙庆 曾垂力

(四川大学计算机学院 成都 610065)

在模式识别和计算机视觉领域,圆检测的应用十分重要。目前,大部分圆检测算法都把关注点放在精确度和检测效率上,随机算法具有计算效率高和占用内存少的优点,然而,随机算法通过选取大量的候选圆并统计落在候选圆上的像素总数判断圆的存在,在实时检测中并不适用。文章提出了一种基于圆的对称性的改进算法,加速了判断候选圆是否为真实圆的过程,同时在统计候选圆上的像素时没有采集图像中全部的边缘像素,而是采集候选圆的内接正方形和外切正方形范围内的边缘像素。实验表明,这种方法在保持圆检测准确性的条件下减少了运算时间。

圆检测;随机算法;高效;对称性

1 引 言

快速与准确的检测圆,在计算机视觉和模式识别领域有着非常广泛的应用前景。近年来,提高运算效率和准确性一直是圆检测研究最主要的关注点[1-7]。当前圆检测研究方法主要可以分为两大类:确定性方法和不确定性方法。其中,大部分确定性方法都是基于Hough变换(Hough Transform)[8]来实现,同时很多关于圆检测的研究是基于 Hough变换进行改进[9-11]。Hough变换是通过将图像从坐标空间变换到参数空间,进而实现圆的拟合。在参数空间不超过两维和干扰较少的图像中,Hough变换往往能达到比较理想的效果,但当空间参数超过两维(如圆的参数空间是三维)时,Hough变换就变得非常不实用,具体表现在:(1)计算量大; (2)占用内存大;(3)提取参数受参数空间量化间隔制约。而Yip等[9]的研究显示,基于随机方法(Randomized Circle-Detection,RCD)的圆检测算法能较好地克服Hough变换的这些缺点。RCD方法的基本思想是:从边缘像素中随机选取4个点,其中任意3个点确定一个圆,假如第四个点正好落在该圆边缘上,就可以把该圆选取作为一个候选圆,然后通过统计落在候选圆边界上边缘像素总数,判断此候选圆是否为一个真实圆。RCD方法很好地避免了Hough变换在参数积累过程中占用大量内存的缺点,但在图像边缘像素较多的情况下,大量的随机选取候选圆和计算落在候选圆上的像素使得运算效率比较低,在多圆并且杂乱重叠的情况下,应用RCD方法变得不现实。为此,本文提出一种基于RCD改进算法(Improved Randomized Circle-Detection, IRCD):(1)在计算落在候选圆像素个数之前,通过圆的对称性排除大量的候选圆,从而加快速度;(2)在计算落在候选圆像素的个数时,仅统计候选圆内接正方形和外切正方形区域的边缘像素是否落在圆形边界上。实验证明,在某些较为复杂的图像中,改进的RCD算法提高了20%～60%的运算效率。

2 基于圆的对称性判断候选圆

一个由4点选取的候选圆如图1所示,它由圆心(x,y)和半径R定义,并令圆心(x,y)为坐标系的原点。设定一个左上角和右下角位置分别是(R,θ+π/36)和(R,θ-π/36)正方形。同时A4、A2分别与A1关于x、y轴对称,A3与A1关于原点对称,vi(i=1,2,3,4)代表正方形区域中的边缘像素集,并且规定其中的边缘像素个数必须大于阈值0.6R(2π/36),其中R(2π/36)表示每个正方形区域内圆形的弧长,该阈值表明每个正方形区域的边缘像素数量要达到弧长的60%才是一个合法的边缘像素集,并且必须同时有两个边缘像素集达到这个阈值才进行对称性计算。假如不满足这个条件,通过改变θ的值(θ=π/4,π/4+△, π/4-△,π/4+2△,…,π/4-4△,其中△= π/18)来搜索满足这个条件的正方形区域,直到找到两个以上对称合法的边缘像素集停止。

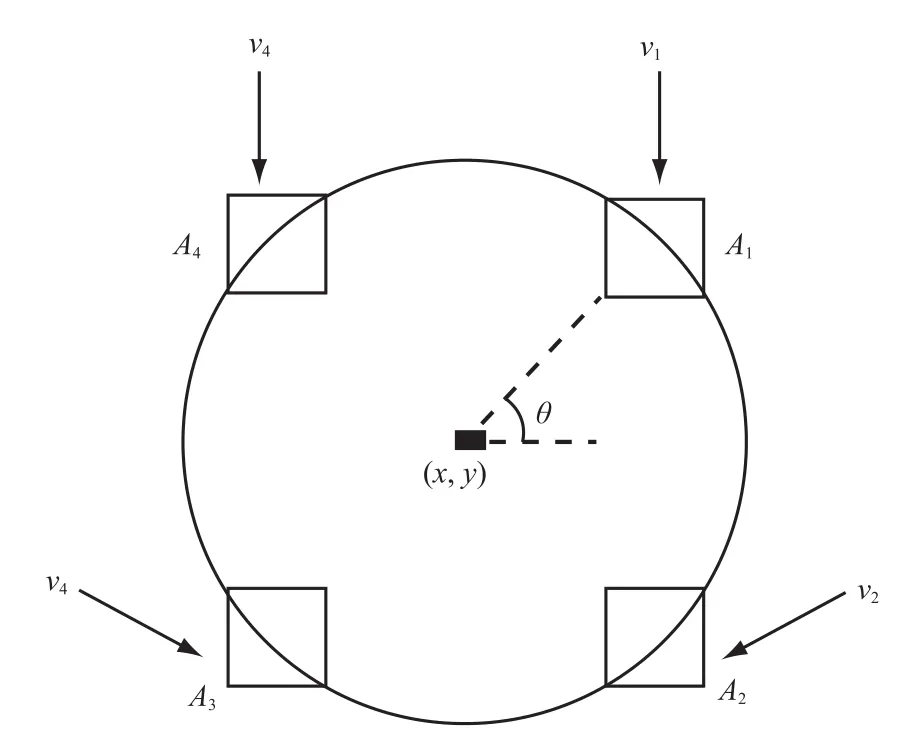
图1 利用边缘像素集测试候选圆的对称性Fig.1 Edge sets used for testing the symmetry feature

假如两个以上的合法边缘像素集已经被找到,基于vk,ve(k,e=1,2,3,4)就可以进行候选圆对称水平的测量。首先,对做映射转换,转换后所得的像素集的意义为:假如vk和ve关于原点对称,那么就是ve围绕圆点(x,y)旋转后的像素集,vk和在坐标系的位置上完全重叠;然后,通过计算vk和ve的Hausdorff距离来测量两者之间的对称水平,由公式(1)表示:

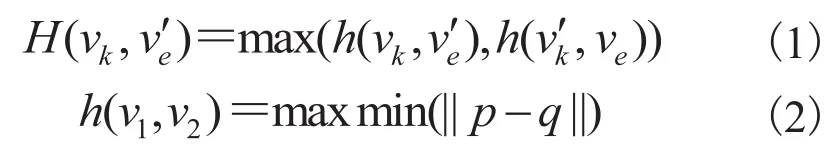
3 统计候选圆上像素的改进方法

在传统的RCD算法中,在通过随机抽取的4点确定一个候选圆以后,需要计算整个图像中的边缘像素与候选圆圆心的距离,以便统计在选取出来的候选圆上边缘像素的数量。当该数量达到预设的某个的阈值后,便可以确定这个候选圆是真实存在的圆形。显然,计算整张图像中的所有边缘像素与候选圆的圆形的过程中会耗费大量的时间,而且很多次的计算是毫无意义的。由于候选圆的边界一定是存在于这个圆的内接正方形和外切正方形之间的区域中,所以在统计落在候选圆边界的像素时只需要考虑这个范围的边缘像素即可,如图2所示。阴影区域为统计落在候选圆上像素总数的采样区域,这个变化对于提高算法效率是显而易见的。

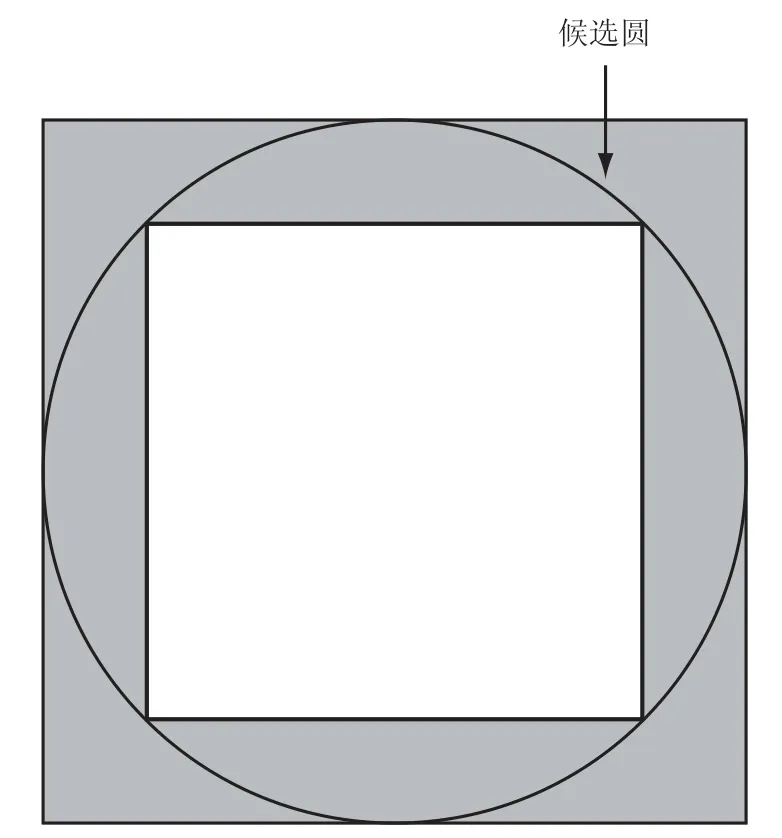
图2 候选圆边界像素统计区域Fig.2 Statistical area of boundary pixels of candidate circle

4 实 验

为了验证本文改进算法的有效性,进行了实验。实验采用Inter Core i5处理器,内存为4G的微机,利用C++编程实现。图3为本文提出的IRCD算法的实验效果图,从实验结果可以看出,无论是干扰较少的简单图像,还是现实生活中较为复杂的原始图像,IRCD算法都可以精确地检测并定位图像中的圆形。表1为本文算法与标准的RCD和随机Hough变换(Randomized Hough Transform,RHT)在不同的噪声条件下执行时间的对比。值得一提的是,由于RHT是目前效果比较好并应用最广泛的Hough变换改进算法,所以实验采用RHT方法而非经典的Hough变换方法进行对比分析。表1显示,在比较简单或噪声较少的图像条件下,RHT方法的效果比RCD和IRCD算法好;当噪声率达到一定的比值时,RCD的效果往往是最好的;但当噪声率的比值非常高或者图像存在较多的干扰时,本文提出的算法在检测效率方面有比较显著的提高。

图3 实验效果Fig.3 Experimental results

表1 三种算法执行时间比较Table 1 Comparison of the execution time of three algorithms

5 结束语

本文提出了一种快速的圆检测随机算法,通过利用圆的对称性,减少了大量候选圆在后期不必要的投票判断是否为真实圆。有效地提高了检测速度,特别是在多圆条件的图像下效果非常明显,并且具有与RCD一样的鲁棒性和占用内存小的优点。下一步的工作,可以利用圆的对称性,并与RHT[12,13]结合,以改进原有的RHT算法。

[1] 蒋联源,苏勤,祝英俊.快速随机 Hough变换多圆检测算法 [J].计算机工程与应用,2009, 45(17):163-166.

[2] 杨四海,陈锻生,谢维波.Hough变换的特性分析:一种全局观点(II)[J].计算机辅助设计与图形学学报,2007,19(1):25-30.

[3] Chung KL,Huang YH.Speed up the computation of randomized algorithms for detecting lines, circles,and ellipses using novel tuning-and LUT-nased voting platform[J].Applied Mathematics and Computation,2007,190(1):132-149.

[4] Lu W,Tan JL.Detection of incomplete ellipse in images with strong noise ny iterative randomized Hough transform(IRHT)[J].Pattern Recognition, 2008,41(4):1268-1279.

[5] Cuevas E,Ortega-Sanchez N,Zaldivar D,et al. Circle detection ny harmony search optimization [J].Journal of Intelligent&Ronotic Systems, 2012,66(3):359-376.

[6] Akinlar C,Topal C.EDCircles:a real-time circle detector with a false detection control[J].Pattern Recognition,2013,46(3):725-740.

[7] Cuevas E,Oliva D,Zaldivar D,et al.Circle detection using electro-magnetism optimization[J]. Information Sciences,2012,182(1):40-55.

[8] Duda RO,Hart PE.Use of the Hough transformation to detect lines and curves in pictures [J].Communications of the ACM,1972,15(1): 11-15.

[9] Yip RKK,Tam PKS,Leung DNK.Modification of Hough transform for circles and ellipses detection using a 2-dimensional array[J].Pattern Recognition,1992,25(9):1007-1022.

[10]Ho CT,Chen LH.Afast ellipse/circle detector using geometric symmetry[J].Pattern Recognition, 1995,28(1):117-124.

[11]Kim HS,Kim JH.A two-step circle detection algorithm from the intersecting chords[J].Pattern Recognition Letters,2001,22(6-7):787-798.

[12]Chen TC,Chung KL.An efficient randomized algorithm for detecting circles[J].Computer Vision and Image Understanding,2001,83(2): 172-191.

[13]Xu L,Oja E,Kultanen P.A new curve detection method:randomized Hough transform(RHT)[J]. Pattern Recognition Letters,1990,11(5):331-338.

An Improved Randomized Algorithm for Circle Detection Based on Geometric Properties of the Circle

SHU Longqing ZENG Chuili
(College of Computer Science,Sichuan University,Chengdu610065,China)

In pattern recognize and computer vision, circle detection is a critical issue. For the moment, the major concern of most circle detection algorithm is ronustness and computational efficiency. Randomzied approaches for circle detection have the advantages of less computational time and less memory requirements. However, randomzied approaches involve in examining a large numner of candidate circles and may not suitanle in real-time applications. In the paper, the symmetry property of the circle was adopted to select the promising candidates for further investigation. At the same time, not all edge pixels in the image, nut the edge pixels netween the inscrined square and exo-square were collected when counting the numner of pixels on the candidate circle. The experimental results show that the proposed algorithm performs fast while maintaining the accuracy.

circle detection； randomzied algorithm； effcient； symmetry

TP 391.4

A

2014-12-18

:2015-01-20

舒龙庆(通讯作者),硕士研究生,研究方向为计算机视觉,模式识别,E-mail:joeyshulongqing@qq.com;曾垂力,硕士研究生,研究方向为图像处理,模式识别。