短期设备状态检修优化决策模型与求解

孙建文，毕四明，陶乾，王晓祥

（国网山东省电力公司泰安供电公司，山东泰安271000）

短期设备状态检修优化决策模型与求解

孙建文，毕四明，陶乾，王晓祥

（国网山东省电力公司泰安供电公司，山东泰安271000）

随着电网规模的不断扩大，输变电设备的检修工作日益得到重视。在电网状态检修背景下，建立了短期设备状态检修优化决策模型。首先，建立了非时齐马尔可夫过程模型用于描述设备的随机停运过程，为便于问题求解，采用阶梯函数逼近设备的时变故障率，而后，依据设备状态转移具有马尔科夫性质，并且结合马尔科夫报酬模型，给出前瞻时间内设备状态概率的求解方法，以及电网检修损失和故障损失的数学表达。最后，以电网检修损失和故障损失二者之和最小为目标，考虑系统状态检修的相关约束条件，构建了短期输变电设备状态检修优化决策模型。通过IEEE-RTS79系统算例验证模型的可行性和有效性。

输变电设备；状态检修；时变故障率；马尔科夫过程；马尔科夫报酬模型

0 引言

合理安排电力设备检修，对保证系统的安全、可靠和经济运行起着重要作用。随着电力系统规模的不断扩大，大容量、高电压设备的投入使用，设备的状态检修工作日益得到重视［1-2］。

一直以来，设备检修策略就是各领域专家和学者研究的热点问题。围绕该问题，传统的设备检修计划是在定期计划检修框架下进行的，设备的故障率通常采用长期历史统计平均值［3-5］。然而，设备在实际运行中，受老化因素影响，故障率具有时变性，对于系统检修决策影响较大，另外，设备状态监测技术的发展，为获取设备的时变故障率提供了现实的基础［6-7］，由此，在设备停运模型中，考虑时变故障率具有重要的理论和现实意义。

现有文献中关于设备停运模型的建立主要有泊松过程和马尔科夫过程两大类。文献［8-12］基于非齐次泊松过程描述设备故障率规律，考虑设备检修前后故障率变化，对系统检修决策建模求解。然而，泊松过程忽略了设备修复率的影响，对于不可忽略设备修复率的情况应该通过马尔可夫过程建模，对此，文献［13］在变电站状态检修决策中，考虑设备的随机停运，建立了多状态停运模型，但由于假设设备任意两状态间的转移率为常数，随着系统中设备数目增加，带来较高的计算复杂度。

在已有研究基础上，计及设备时变故障率和维修时间随机性，基于随机过程理论，建立了短期设备状态检修优化决策模型。首先，通过非齐次马尔科夫过程描述设备的随机停运过程，为便于问题求解，借鉴文献［14］，采用阶梯函数逼近设备时变故障率，然后，依据马尔科夫报酬模型，给出前瞻时间内设备状态概率的求解方法，以及系统检修损失和故障损失的数学表达，最后，以系统检修损失和故障损失二者之和最小为目标，建立了输变电设备状态检修优化决策模型。

1 设备的时变停运模型

电力设备在实际运行过程中，外部随机因素和自身老化均可导致其发生故障。考虑老化因素的影响，建立设备的两状态马尔科夫过程模型。图1给出了设备正常和故障两种状态的转移过程，其中0为工作状态，1为故障状态。前瞻时间内，由于设备老化的影响，故障率为时变量，实际应用中，可通过威布尔分布表示，修复率设为常数，由此可知，其转移规律符合非齐次马尔科夫过程。

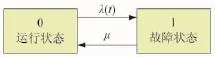
图1 设备的两种状态转移过程

设备时变停运模型中状态转移参数为时变量，直接求解随机过程微分方程会很复杂，为便于问题求解，采用文献［14］的方法，通过阶梯函数对设备故障率进行逼近。前瞻时间内，以时段为单位将设备时变的故障率离散化，使任一时段，设备故障率为常数，由此可知，单个时段设备的状态转移具有齐次马尔科夫性质，可通过齐次马尔科夫方程进行设备的概率特性分析。

2 前瞻时间内设备状态概率表达

前瞻时间内，通过预防性检修，可以延缓甚至消除设备故障隐患，这与设备所采取的检修策略有关。目前，在设备状态检修决策中，现有文献多采用役龄回退因子的概念描述检修对设备性能的改善，以对检修之后设备的故障率进行预测，从而建立设备的不完全检修模型，本文在此依然沿用，关于该模型的相关概念及具体内容可见文献［15］。

前瞻时间内，在设备故障率预测基础上，对于任一时段k，依据设备状态转移过程具有齐次马尔科夫性，可建立其福克—普朗克（Forkker-Planck）方程（又称“状态方程”）［16］，求取设备在该时段的状态转移概率函数，记为Pi，T（k），具体表达如下

式中：πi，jl（k）为设备i在时段k由状态j转移到状态l的概率，j，l∈｛0，1｝。

前瞻时间，时段k内设备i的状态概率为

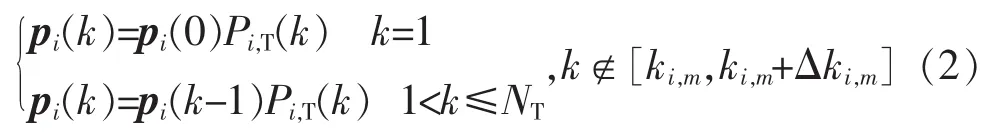
式中：pi（k）＝［pi，0（k）pi，1（k）］为时段k设备i的状态概率向量，其中pi，j（k）表示设备在时刻k处于状态j的概率，j∈｛0，1｝；ki，m为设备i在前瞻时间内的检修开始时段；Δki，m为设备i进行检修所持续的时段数。

3 电网的检修损失和故障损失

3.1 设备个体故障损失

前瞻时间内任一时段k内，求取设备i由正常状态向故障状态转移率，根据马尔科夫报酬模型的原理［17］，其微分方程表达为

式中：λki为待修设备i在时段k故障率；Vi，j（k，t）为初始状态为j时待修设备i在时刻t的累积转移率函数，j∈｛0，1｝。

通过求解上述微分方程，可得时段k待修设备i的累积转移率函数Vi，0（k，t）和Vi，1（k，t）为

前瞻时间内，设备在时段k的转移率还与设备的状态概率有关，设单位时段长度为Δt，则设备i由正常运行状态向故障状态的转移率为

式中：pi，0（k-1）和pi，1（k-1）为设备i时段k-1处于状态正常和故障状态的概率。

前瞻时间内，设备个体故障风险为

式中：NM为前瞻时间内电网待修设备数目；NT为前瞻时间划分的时段数；Ci，F为设备i故障后维修需要的费用。

3.2 设备个体检修损失

前瞻时间内，设备个体检修费用为

式中：Ci，M为设备i进行检修的费用；Xi，t表示设备在时段t是否开始进行检修。

3.3 系统的检修损失和故障损失

前瞻时间内，设备检修引起的损失包括两部分：一是设备检修引起的直接损失，指系统计划切负荷损失；二是在设备检修对应的计划切负荷损失基础上，设备随机故障引起的系统随机切负荷损失，为反映损失发生的概率及严重程度，可通过概率与后果的乘积，求取期望切负荷（EENS）。由于二者的价值不同，分别进行求解。前瞻时间内，系统整体的检修损失和故障损失统一表示为

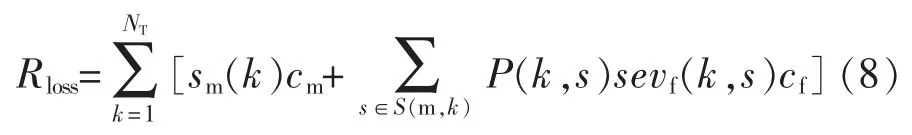
式中：sm（k）为时段k设备检修引起的系统计划切负荷；cm为计划失负荷单位损失；S（m，k）为时段k计及设备检修，系统的事故集合；sevf（k，s）为时段k事故s对应的系统随机失负荷；cf为系统随机失负荷单位损失；P（k，s）为时段k系统状态s出现的概率，数学表达为

式中：ns（k）和ms（k）分别为时段k计及设备检修事故s中工作和故障的设备数目。

4 输变电设备状态检修优化决策模型

4.1 模型建立

以前瞻时间内电网检修损失和故障损失二者之和最小为目标建模，其数学描述

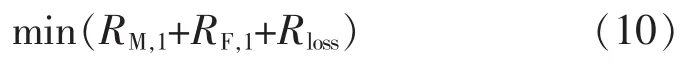
约束条件为：

1）检修资源约束。

式中：Xi，k为时段k设备i是否处于检修停运状态；ri为设备i检修对资源的需求量；r（k）为时段k内系统资源可用量。

2）设备同时检修约束。对于引起系统重复停电的设备，应该将其安排一起进行检修，满足

4.2 模型求解

输变电设备状态检修优化决策是一个复杂的组合优化问题，本文采用遗传算法进行求解，具体求解流程如图2所示。

图2 模型的求解流程

5 算例及分析

为阐述本文研究的有效性，以IEEE-RTS79系统为例进行分析。前瞻时间内，确定系统中5台变压器（设备3-24，9-11，9-12，10-11和10-12）为待修设备，设定变压器平均修复时间为20天，假设其他输变电设备在前瞻时间内均可靠运行，设备状态的相关信息表1，电网详细参数可见文献［18］。前瞻时间为1年，以2周为单位，将全年划分为26个时段，前瞻时间内，每个设备只考虑一种检修方式，系统计划失负荷单位损失和随机失负荷单位损失分别为0.053万元／MWh和1.053万元/MWh。

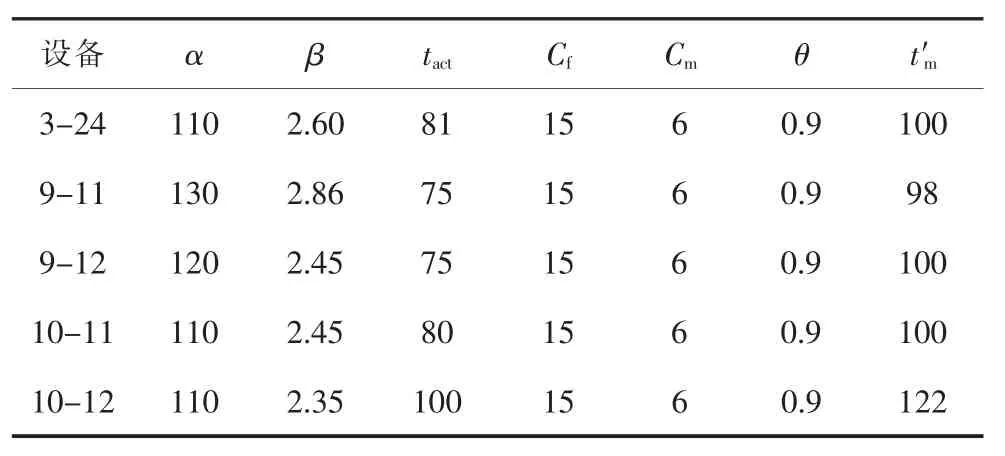
表1 IEEE-RTS79电网设备信息

5.1 系统不同检修策略分析

本算例对应3种方案进行决策。

方案1：按照设备个体性能进行检修决策。

方案2：前瞻时间内待修设备只安排检修一次。

方案3：本文方法。

对应上述3种检修方案一一进行求解，表2和表3为3种方案的决策结果。其中，表2中检修时段是指以2周为单位，将全年划分为26个时段，数据表示的是设备的检修时段。

表2 方案1～3设备检修计划检修时段安排

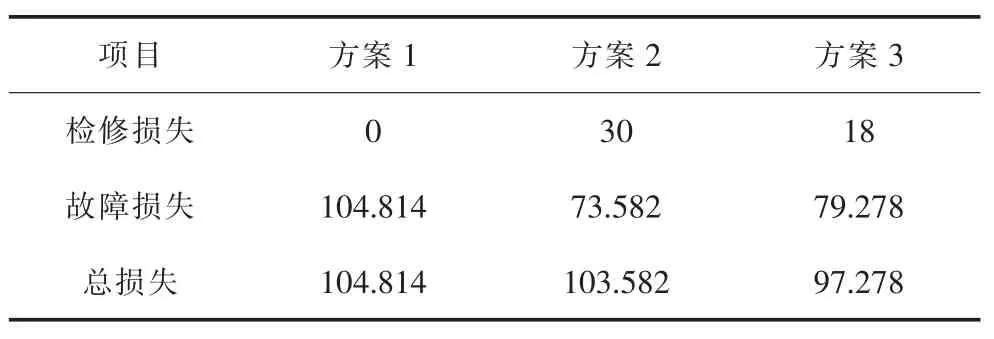
表3 IEEE-RTS79系统损失万元

方案1只考虑设备个体性能，由于前瞻时间内设备个体故障损失较小，因此，决策结果为设备均不需要安排检修，但却造成很大的系统损失，如表3所示。

对比方案2与方案1可知，检修决策中由于考虑了系统损失，使该方案对应的系统总损失有所降低。

对比方案3与方案2可知，前瞻时间内，待修设备中3-24和9-12不需要安排检修，该方案对应的系统总损失进一步降低。

上述算例表明，方案1只考虑设备个体性能，未考虑系统损失，使前瞻时间内系统总损失最大；方案2通过预防性检修，减小了系统故障损失，但对于系统经济性的提高有限，还是难以避免设备过修或欠修的情况；方案3以系统总损失最小为目标进行检修决策，前瞻时间内对应的系统总损失在3种方案中最小，反映了本文方法是有效的，有利于提高系统整体的经济效益。

5.2 维修停运随机性的影响

电网中设备的平均修复时间差别较大，如对于输电线路而言，平均修复时间为1~99 h，而对于一些大型设备，如变压器和机组，平均修复时间可达10~99天，因此，在建模时需要具体情况具体分析。为定量分析设备维修停运随机性对检修决策的影响，该算例对应2种方案进行决策：方案4和方案5分别设定设备的平均修复时间为10天和5天，表4为2种方案的决策结果。

表4 方案4～5设备检修计划检修时段安排

由表4可知，前瞻时间内，方案4只有设备9-12检修1次，方案5中设备均不检修，说明状态检修是与设备个体性能、修复率等因素有关复杂的优化决策问题，研究中应该从系统整体角度进行决策。

6 结语

针对短期输变电设备状态检修决策的特征，考虑设备时变的故障率和维修时间随机性，建立了设备的随机停运模型，并基于通过概率特性分析，从检修损失与故障损失两个角度协调设备检修时机与系统风险水平，以二者之和作为协调程度优劣的标准，并通过算例进行验证。

设备时变的故障率与维修时间随机性影响设备的检修时机，在制定检修策略时需要予以考虑。检修损失和故障损失可以充分量化设备检修时机与系统运行风险之间的关联性，有效协调和处理各方面矛盾，追求二者之和最小可以实现电网最优决策。

［1］巩宪锋，衣红钢，王长松，等.高压开关柜隔离触头温度监测研究［J］.中国电机工程学报，2006，26（1）：155-158.

［2］Ascebrenner D，Kranz H G，Rutger W R，et al.On line PD measurements and diagnosis on power transformers［J］.IEEE Transactions on Dielectrics and Electrical Insulation，2005，12（2）：216-222.

［3］丁明，冯永青.发输电设备联合检修安排模型及算法研究［J］.中国电机工程学报，2004，24（5）：18-23.

［4］Li Wenyuan，Korczynski J.A reliability-based approach to transmission maintenance planning and its application in BC hydro system［J］.IEEE Transactions on Power Delivery，2004，19（1）：303-308.

［5］于大洋，韩学山，赵建国.发输电协调检修计划的主从规划模型与分区搜索算法［J］.电网技术，2010，34（4）：88-93.

［6］潘乐真，张焰，愈国勤，等.状态检修决策中的电气设备故障率推算［J］.电力自动化设备，2010，30（2）：91-94.

［7］Ning Liaoyi，Wu Wenchuan，Zhang Boming，etc.A time-varying transformer outage model for on-line operational risk assessment［J］.International Journal of Electric Power and Energy System，2011，33（3）：600-607.

［8］潘乐真，鲁国起，张焰，等.基于风险综合评判的设备状态检修决策优化［J］.电力系统自动化，2010，34（11）：28-32，66.

［9］高卫恒，王建学，路建明，等.基于等风险度的输电系统检修计划［J］.电力系统自动化，2012，36（7）：6-11.

［10］Abiri-Jahromi A，Fotuhi-Firuzabad M，Parvania M.Optimized midterm preventive maintenance outage scheduling of thermal generating units［J］.IEEE Transactions on Power Systems，vol.27，no.3，pp.1 354-1 365，Aug.2012.

［11］A.Abiri，M.Parvania，F.Bouffard，andM.Fotuhi.A Two-Stage Framework for Power Transformer Asset Main tenance Management-Part I：Models and Formulations［J］.IEEE Transactions on Power Systems，vol.28，no.2，pp.1395-1403，May.2013.

［12］A.Abiri，M.Parvania，F.Bouffard，and M.Fotuhi.A two-stage framework for power transformer asset maintenance management-Part II：Validation results［J］.IEEE Transactions on Power Systems，vol.28，no.2，pp.1 404-1 414，May.2013.

［13］李明，韩学山，王勇，等.变电站状态检修决策模型与求解［J］.中国电机工程学报，2012，32（25）：196-202.

［14］Lisnianski，A.，I.Frenkel and Y.Ding.2010.Multi-state System Reliability Analysis and Optimization for Engineers and Industrial Managers.London：Springer.

［15］Tan C M and Raghavan N.A framework to practical predictive maintenance modeling for multi-state systems［J］.Reliability Engineering and System Safety，2008，93：1 138-1 150.

［16］李文沅.电力系统风险评估模型、方法和应用［M］.北京：科学出版社，2006：10-34.

［17］Lisnianski A and Levitin G.Multi-state system reliability：Assessment，optimization and applications［M］.World-Scientific，Singapore，2003.

［18］Subcommittee P M.IEEE reliability test system［J］.IEEE Transactions on Power Apparatus and Systems，1979，98（6）：2 047-2 054.

Short-term Decision-making Model and Solution of Condition-based Maintenance for Power Equipment

SUN Jianwen，BI Siming，TAO Qian，WANG Xiaoxiang（State Grid Taian Power Supply Company，Taian 271000，China）

With the development of power systems，equipment maintenance receives more and more attention.Based on equipment condition-based maintenance，the short-term maintenance scheduling model of power system is proposed.Firstly non-homogeneous Markov process is used to describe equipment stochastic process.For simplicity，staircase function is used to approximate equipment time-varying failure rate.And then，Markov process and Markov reward model are used to obtain equipment state probability and system maintenance loss as well as system failure loss.Finally，system maintenance scheduling model is given minimizing the sum of system maintenance loss and failure loss while considering system maintenance constraints.Validity and feasibility of the model are illustrated through the IEEE-RTS79 system.

power equipment；condition-based maintenance；time-varying failure rate；Markov process；Markov reward model

TM711

A

1007－9904（2015）05－0028－05

2014-12-30

孙建文（1988），男，主要从事变电站运行维护，状态巡视、检修等工作。