基于电网固有结构特性的配电网最优无功补偿方法
2015-01-07赵岩蒋哲孙东磊韩学山麻常辉李文博武乃虎
赵岩,蒋哲,孙东磊,韩学山,麻常辉,李文博,武乃虎
(1.国网山东省电力公司电力科学研究院,济南250002;2.电网智能化调度与控制教育部重点实验室(山东大学),济南250061)
·试验研究·
基于电网固有结构特性的配电网最优无功补偿方法
赵岩1,蒋哲1,孙东磊2,韩学山2,麻常辉1,李文博1,武乃虎1
(1.国网山东省电力公司电力科学研究院,济南250002;2.电网智能化调度与控制教育部重点实验室(山东大学),济南250061)
提出了一种基于电网固有结构特性的配电网最优无功补偿方法。首先根据无功就地平衡的原则,以无功补偿节点为分解点划分子系统,并在子系统内基于电网固有结构特性确定无功补偿容量,以此确定系统运行的最优补偿,然后在有无功补偿容量受限的情况下,采用启发式的回推算法修正补偿方案,最后基于电网结构调整以顺应系统源流特性的原则,确定最终的无功补偿方案。算例分析验证了所提方法的准确性和计算效率。所提方法不仅可用于配电网电容器快速最优投切决策,还对配电网最优无功补偿配置具有重要作用,具有良好的实际应用前景。
配电网;无功补偿;电网固有结构特性
0 引言
配电网无功补偿是降低系统网损和提高电网电压水平的一种有效而经济的手段,从电气特性角度看,无功补偿的目的就是实现无功功率的就地平衡。
配电网最优无功补偿问题从数学意义上讲属于非线性整数规划范畴,目前主要的研究方法为数学规划法[1-3]和人工智能搜索方法[4-5]。数学规划方法计算速度快,但计算条件较为苛刻,对电网数据的精确性依赖性强,计算效果鲁棒性差,而且对初值很敏感,易陷入局部最优解。人工智能的理论和方法虽然能克服数学规划方法易陷入局部最优解的缺点,但存在计算时间长、易陷入维数灾等缺点。因此,如何实现配电网最优无功补偿问题的高效求解以满足工程应用需求值得深入研究,这也是研究的出发点。
电网的结构特性主导着电力系统的潮流状态[6]。由欧姆定律可知,给定条件下,电力系统潮流一定是自动满足网损最小的路径[7]。在负荷需求确定的情况下,存在一种源的分配使得流顺应电网特性达到网损最小[8];在节点注入(源、荷)确定的情况下,一定存在与源相适应的电网结构使得配网以最小网损运行。基于该辩证关系提出了一种配电网无功补偿方法来决策无功流的分布使得配网网损最小。
提出了一种新的配电网最优无功补偿的启发式算法,该算法基于电网固有结构特性。首先根据无功就地平衡的原则,以电容器补偿节点为分解点划分子系统,并在子系统内基于电网固有特性确定无功补偿容量,然后采用启发式的回推算法修正补偿方案,最后基于电网结构调整以顺应系统源流特性的原则,确定最终的无功补偿方案。美国PG&E 69节点配电系统算例分析验证了所提方法的准确性和计算效率。
1 电网固有结构特性
根据欧姆定律,节点注入电流I和节点电压V的关系满足节点导纳方程:

式中:Y为节点导纳矩阵。若把电源和负荷分开表示,则式(1)可写成分块矩阵的形式:

式中:IG、IL、VG和VL分别为电源和负荷节点注入电流和节点电压向量。YGG、YGL、YLG和YLL为区分电源节点和负荷节点后节点导纳矩阵Y的各子阵。
式(2)可变换为混合参数方程形式:
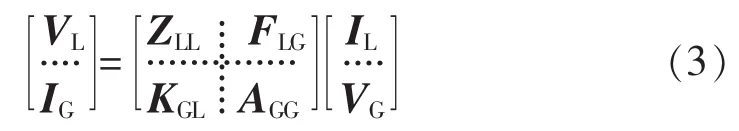
矩阵ZLL为负荷间互联阻抗,其对应着为满足负荷用电需求而必须产生的电网损耗。矩阵FLG为负荷与电源的互联矩阵,该矩阵每行元素的绝对值可视为各电源与该负荷的相对电气距离,蕴含着满足负荷功率需求的最佳电源出力分配方案[6]。此外,矩阵FLG还包含了电网结构特性对网损的贡献[9]。矩阵,其含义同FLG。由分块矩阵理论可知,矩阵AGG为节点导纳矩阵Y中子阵YLL的Schur补,其为消去负荷节点后各电源间的互联导纳矩阵,对应着电源间环流产生的电网损耗。
2 配电网最优无功补偿方法
以图1所示的简单辐射型配电网为例,阐述基于电网固有结构特性的配电网最优无功补偿方法。

图1 简单辐射型配电网示意图
2.1 划分子系统
根据无功就地平衡的原则,以无功电源节点为分解点划分子系统,各子系统如表1所示。划分的子系统分为三类:子系统1、2为第一类,该类的特点为无功电源为辐射状电网的末端电容器节点,该节点及其下游节点的无功负荷均应由其补偿;子系统3为第二类,该类的特点是两端为无功电源节点;子系统4为第三类,该类的特点是含有节点的度大于2的节点,其无功电源节点个数≥3。作为分解点,每个无功补偿节点的最优补偿量对应着其所关联的各子系统对该节点的最优无功补偿需求。

表1 子系统表
2.2 子系统无功补偿算法
第一类子系统对无功电源节点的无功补偿需求是明确的,其大小即为各节点无功负荷之和。
对第二类和第三类子系统来说,存在无功需求在无功电源节点的分配问题。无功流动对网损的贡献体现为I2QR,其中IQ表示无功电流,R为支路阻抗。以网损最小为无功分配原则,子系统3的无功分配问题可表示为以下优化问题:

式中:R5、R6、ID6、IQ5和IQ7分别为支路5-6电阻、支路7-6电阻、节点6无功负荷电流、节点5和节点7为满足节点6无功负荷而注入的无功电流,如图2所示。

图2 子系统3示意图
求解式(4)所述优化问题,得

即无功电流按照电阻值进行经济分配。
若将图2所示子系统3看成直流纯电阻电网,则根据欧姆定律可知有以下关系:

式中:I5、I6、I7、V5、V6和V7分别为节点5、节点6和节点7的注入电流和节点电压。结合式(6)和式(3)可得

对比式(6)和式(3),可以看出矩阵FLG即体现了经济最优无功补偿分配方案。对于子系统4,经验证,其最优分配同其对应的FLG阵一致。
因此,可以推测对第二类和第三类子系统,其最优无功分配同其对应的FLG阵一致。上述推测显然是合理的,其类似于以网损最小为目标的最佳电源出力分配方案[8]。对于第一类子系统,其对应的FLG阵各元素均为1,其最优无功分配同其对应的FLG阵也表现为一致。
综上,在各无功补偿节点补偿容量充足时,忽略节点电压幅值差异,可通过下式确定各子系统无功补偿节点的无功补偿量,即
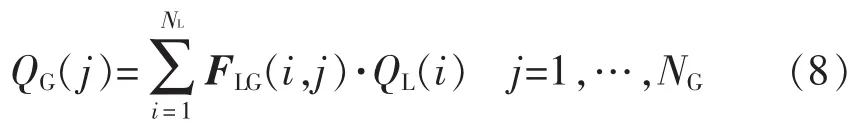
式中:FLG(i,j)表示矩阵FLG中第i行第j列元素,对应第i个负荷节点和第j个无功电源节点;NL和NG分别表示子系统负荷节点数和无功电源节点数;QL(i)表示第i个负荷节点;QG(j)表示第j个无功电源节点。
当无功电源节点补偿容量受限时,采取以下启发式原则进行修正。
1)当系统末端无功电源节点7或11不足以满足其自身以及下游节点负荷无功需求而存在缺额、而其前一个补偿节点无功容量充足时,则由其前一个补偿节点增加补偿量以弥补缺额;
2)当节点5补偿存在缺额时,而节点7无功容量充足时,增加节点7无功补偿量,但其补偿总量不应超过5节点下游负荷无功需求总量;
3)若按原则2仍无法满足无功需求时,则不再把5节点视为无功补偿源,而是看成由其完全补偿以及其下游补偿点确定后的等值无功负荷节点,这样更改后修改矩阵FLG重新确定对应子系统最优无功决策量。
2.3 全网无功补偿优化
电容器可视为并联对地支路,电容器的投切对应着电网结构特性的变化,进而影响网损。网损PLoss可表示为

式中:i∈j表示节点i和节点j直接相连;gij为支路i-j的电导,该支路首末节点分别为节点i、节点j;V为节点电压相量。以网损最小为目标就对应着最小化线路两端电压相量差。
在辐射网中VG对应根节点电压,VL可根据式(3)得到:

由于负荷电流IL基本上不会受无功补偿的影响,电容器的投切对应着电网结构的改变就体现在ZLL上。因此,以网损为目的的电容器的投切决策就对应着改变不同的映射矩阵ZLL将IL-YLGVG映射到对应的n-1维电压复相量空间,使得PLoss减小。具体实现流程如下。
1)离线制定不同无功补偿组合下的ZLL表;
2)潮流计算或广域量测计算各相关相量;
3)查解空间内的ZLL表,由式(6)计算各组合下的网损值,选择最佳组合。
2.4 算法总体流程
提出的基于电网固有结构特性的配电网最优无功补偿方法的具体步骤如下。
1)从根节点开始按照深度优先搜索方法给节点编号;
2)在编号的同时划分子系统,根节点开始标记为第一个子系统,自根节点开始到搜索到下一个电容器节点前的路径上的所有节点都属于当前子系统,每遇到电容器节点,子系统编号加1,在回溯搜索过程中的节点与其相连的已编号节点属于同一子系统;
3)形成各子系统纯电阻网络的节点阻抗矩阵,根据式(5)计算各子系统对应的FLG矩阵;
4)根据当前负荷无功功率计算各子系统最优补偿量;
5)判断各电容器节点能否满足无功补偿需求,若不能,继续至6,否则转至7;
6)按照以上原则1~3回推形式修正补偿方案;
7)根据修正后的补偿方案缩减解空间,具体为电容器节点补偿方案为处于全补偿或完全退出时,固定该节点补偿方案,若存在向上或向下的补偿裕度时,将其相邻的整组作为待确定的补偿解,为弥补未考虑网络无功损耗带来的影响,取相邻的向上两个离散作为待确定的补偿解;
8)根据修正补偿方案计算潮流或根据当前的潮流量测,确定IL,根据式(10)遍历解空间确定最终的补偿方案。
需要说明的是,步骤1~3可离线进行;步骤3、4、7和8可并行计算。此外,为进一步提高计算效率,还可进行配电网图结构简化,即将一些无电容器节点的侧支路用相关主干支路节点上的等效负荷代替。
3 算例分析
算例仿真在主频为3.1 GHz、内存为8 GB的计算机上进行,依托MATLAB平台编写基于电网固有结构特性的配电网最优无功补偿程序。
3.1 算例描述
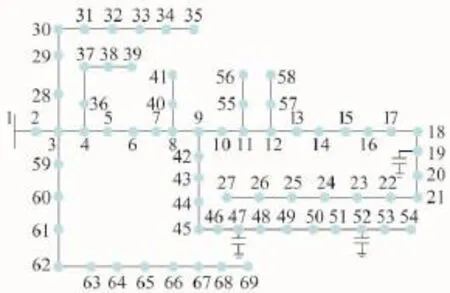
图3 PG&E 69节点配电系统
以图3所示的PG&E 69节点配电系统[10]为例,该系统基准容量为10 MVA,基准电压为12.66 kV,节点19、47和52为电容器节点,电容器参数如表2所示。

表2 电容器参数
3.2 算例计算与分析
基于无功就地平衡的原则划分子系统,子系统划分情况如表3所示,子系统无功补偿方案如表4所示。

表3 子系统

表4 子系统最优无功补偿方案
从表4可以看出系统节点19的无功补偿需求超过了其补偿容量上限,固定其最大补偿容量,将其看成无功负荷节点,修改子系统4,重新决策其无功补偿方案,结果如表5所示。

表5 修正后的子系统4无功补偿方案
修正后的系统无功补偿方案如表6所示。

表6 修正后的无功补偿方案
基于表6给出的无功补偿方案,计算潮流以及确定无功投切解空间,如表7所示。

表7 缩减后的解空间
根据式(6)遍历解空间确定最终的投切方案如表8所示。

表8 电容器投切方案
表8所示投切方案与文献[4]相同,但由于根据电网固有结构特性采用了启发式规则,有效缩减了解空间,计算效率得以提高。以PG&E 69节点系统为例,本文方法与传统方法的计算效率对比如表9所示。

表9 计算效率对比
由表9可知,文献[4]方法即人工智能搜索方法计算时间最长,文献[3]方法即数学规划方法计算时间次之,而本文启发式方法计算时间最短。因此,相对于传统方法,本文方法在计算效率上得到很大提高。
4 结语
基于电网固有结构特性提出了一种新的配电网最优无功补偿的启发式方法。首先根据无功就地平衡的原则,以电容器补偿节点为分解点划分子系统,并在子系统内基于电网固有特性确定无功补偿容量,以此确定系统运行的最优补偿,然后在有无功补偿容量受限的情况下,采用启发式的回推算法修正补偿方案,最后基于电网结构调整以顺应系统源流特性的原则,确定最终的无功补偿方案。算例分析验证了所提方法的准确性和计算效率。所提方法准确性高,不仅适用于电容器快速最优投切决策,还对配电网最优无功补偿配置具有重要作用。所提方法计算效率高,具有良好的实际应用前景。
[1]潘珂,韩学山,孟祥星.无功优化内点法中非线性方程组求解规律研究[J].电网技术,2006,30(19):59-65.
[2]吴文传,张伯明.电容器实时优化投切的最优匹配注入流法[J].中国电机工程学报,2004,24(1):35-39.
[3]王威,韩学山,王勇,等.配电网络电容器优化投切的作用范围法[J].电力系统及其自动化学报,2009,20(6):36-40.
[4]郝文波,于继来.配电网电容器优化投切的制约进化策略[J].电力系统自动化,2006,30(12):47-52.
[5]邓集祥,张弘鹏.用改进的Tableu搜索方法优化补偿电容器分档投切的研究[J].电网技术,2000,24(2):46-49.
[6]S ikiru T H,Jimoh A A,Hamam Y.Inherent structural characteristic indices of power system networks[J].Electrical Power and Energy Systems,2013,47:218-224.
[7]Ahuja R K,Magnanti T L,Orlin J B.网络流理论,算法与应用(英文版)[M].北京:机械工业出版社,2005.
[8]Thukaram D,Vyjayanthi C.Evaluation of Suitable Locations for Generation Expansion in Restructured Power Systems:A Novel Concept of T-index[J].International Journal of Emerging Electric Power Systems,2009,10(1):1-24.
[9]Abdelkader S M.Characterization of transmission losses[J].IEEE Trans.on Power Systems,2011,26(1):392-400.
[10]刘健,毕鹏翔,董海鹏,等.复杂配电网简化分析与优化[M].北京:中国电力出版社,2002.
Optimal Reactive Compensation Method for Distribution System Based on Inherent Structural Characteristics
ZHAO Yan1,JIANG Zhe1,SUN Donglei2,HAN Xueshan2,MA Changhui1,LI Wenbo1,WU Naihu1
(1.Electrical Power Institute of State Grid Shandong Electric Power Company,Jinan 250002,China;2.Key Laboratory of Power System Intelligent Dispatch and Control of Ministry of Education(Shandong University),Jinan 250061,China)
In this paper,we propose a novel method of optimal reactive compensation for distribution system based on inherent structural characteristics.Firstly,following the reactive power local-balance rule,the distribution system is divided into several subsystems with the reactive compensation buses as the cut-off nodes,then the optimal sizing of reactive compensation is determined within the subsystems based on the inherent structural characteristics of networks.Secondly,the revised compensation scheme is determined by heuristic backward sweep method in case the reactive compensation capacity is constrained.Finally,the ultimate scheme for reactive compensation is determined based on the rule that the adjustment of network structure should adapt to the characteristics of source and power flow.Case study shows the effectiveness and efficiency of the proposed method.The proposed method can be not only used for decision making of the optimal sizing of capacitors,but also useful for optimal configuration of reactive compensation,therefore,it has great utility prospects.
distribution system;reactive power compensation;inherent structural characteristics
TM732;TM711
A
1007-9904(2015)05-0001-05
2014-12-30
赵岩(1963),男,高级工程师,主要从事电力系统运行与控制相关研究;
蒋哲(1985),男,工程师,从事电动汽车相关领域研究工作;
孙东磊(1988),男,博士研究生,主要从事电力系统源网协同理论研究工作;
韩学山(1959),男,教授,博士生导师,主要从事电力系统运行分析与控制、优化调度、EMS及电力系统经济方面的研究和教学工作。
国家自然科学基金项目(51177091,51477091)、国家重点基础研究发展计划项目(973计划)(2013CB228205)共同资助。
