基于样本熵的电网电压稳定性能分析

尹茂林，张学清，施东明，林山，张玉亭，邢华，蒋鹏

（国网山东省电力公司济南供电公司，济南250061）

基于样本熵的电网电压稳定性能分析

尹茂林，张学清，施东明，林山，张玉亭，邢华，蒋鹏

（国网山东省电力公司济南供电公司，济南250061）

为了分析电网中电压稳定的薄弱节点，提出一种基于幅值序列波动强度和样本熵的电压稳定性能分析方法。首先通过电力系统仿真软件得到电网电压波动的幅值信息，然后依据各负荷节点电压幅值波动序列的波动强度数值，选取进行电压稳定性能分析的最佳序列长度，在此基础上利用动力学中的平坦因子理论提取了每个时段的电压幅值平坦因子，由此构造了一种利用样本熵理论确定电网中电压薄弱节点的方法。最后以某年山东电网冬季运行方式潮流数据为断面，利用传统电压分析理论（如戴维南等值法、连续潮流法）验证所提方法的有效性，为电网的运行与规划提供有益参考。

电网；波动强度；电压稳定性；样本熵

0 引言

现代工业的高速发展，电网往往接近于满载运行，电网负荷侧的稳定问题日益引起电力工作者的重视，如何快速寻求电网中电压稳定性能的薄弱点，对于电网调度运行管理部门指导实际电网的运行具有重要的作用。传统电压稳定性分析如戴维南等值法［1-2］、连续潮流法［3-4］、灵敏度分析法［5］和模态分析法［6］等，未涉及电网运行中负荷侧动态特性对系统电压稳定性能的影响。本文拟通过引入电网的动态特性特征进行电压稳定性能评估［6-7］。近年来，混沌以及分形理论在电力系统分析和控制中得到了普遍应用，文献［8］提出电力系统存在混沌不变集，且认为Hopf分岔可能导致电压崩溃。文献［9］将混沌理论与传统的神经网络理论相结合用于电力系统短期负荷预测，取得了较好的效果。

信息熵可以表征信息的平均不确定性［10］。在信息熵基础上发展起来的混沌理论的柯尔莫哥洛夫熵以及近似熵理论，近年来已经在许多领域得到了广泛应用。但存在一些缺陷，例如：柯尔莫哥洛夫熵需要用较长数据进行稳健分析；近似熵虽然使用较短数据就可进行稳健分析，但容易在分析时引起较大误差。由Richman提出的与近似熵理论类似的样本熵理论［11］能很好避免近似熵的缺陷，已经在生物医学［12-13］和水文学［14］方面广泛应用，而在电力系统方面应用较少。

建立了一种利用电网负荷变化动态信息评判电网稳定性能的方法。首先负荷扰动量按Weibull分布仿真依次递增区域内各个负荷节点功率，得到电网各个节点的电压幅值信息。在此基础上利用动力学的波动强度理论并结合样本熵理论，完成对电网电压稳定薄弱节点评估的研究。

1 相关理论

1.1 波动强度

波动强度是可以表征数据序列曲线波动程度的一种统计物理概念［15］，可表示为

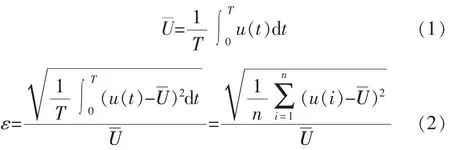
式中：ε为波动强度；n为数据序列的点数；T为采样周期；u（t）为各点幅值大小；U为序列幅值的平均值；u（i）为第个采样点的幅值。

1.2 平坦因子

平坦因子是广泛应用动力学中的一种统计物理概念［16］，其数学表达式为

式中：F为平坦因子；k为序列的点数。

1.3 相空间重构

由混沌理论［17］知，对于一给定的标量时间序列｛xi｝，i＝1，2，…，N（N为数据总数），进行相空间重构，即Xi＝｛xi，xi+τ，…，xi+（m-1）τ｝，i＝1，2，…，M。其中为混沌相空间重构的嵌入维数，M＝N-（m-1）τ为混沌相空间的点数，τ为时间延迟。本文采用自相关系数法和Cao氏法［16］分别计算相空间重构的时间延迟τ和嵌入维数。

2 样本熵

样本熵是由Richman提出的一种新的序列复杂性测度方法［14］。可用SampEn（N，m，r）表示。样本熵相对于近似熵在算法上计算的是和的对数，可更准确估计条件概率。其具体算法如下。

假设时间序列｛xi｝为x（1），x（2），…，x（N），r为预先选定的相似容限。

1）将序列｛xi｝按顺序组成m维矢量，即X（i）＝［x（i），x（i+1），…，x（i+m-1）］，其中i＝1，2，…，N-m+1。

2）定义两者X（i）与X（j）（j=1，2，…，N-m+1，且j≠i）之间的距离dm［X（i），X（j）］为两者对应元素差值最大的一个，即，对于每一个i值计算X（i）与其余矢量X（j）之间的dm［X（i），X（j）］。

3）对于给定的相似容限r（r＞0），对每一个值统计dm［X（i），X（j）］＜r的数目，然后计算其与距离总数N-m的比值，记作Bmi（r），即，（i＝1，2，…，N-m+1且i≠j），num为数目。该过程称为X（i）模板匹配过程，表示任一个X（j）与模板的匹配概率。

5）增加维数为m+1，构造一组m+1维矢量，即［x（i），x（i+1），…，x（i+m）］，其中i＝1，2，…，N-m。

6）定义两者X（i）与X（j）（j＝1，2，…，N-m，且j≠i）之间的距离dm+1［X（i），X（j）］为两者对应元素差值最大的一个，即，对于每一个i值计算X（i）与其余矢量X（i）之间的dm+1［X（i），X（j）］。

7）采用与第3）步类似的形式，计算其与距离总数N-m-1的比值，记作Bm+1i（r），即num｛dm+1［X（i），X（j）］＜r｝，（i＝1，2，…，N-m且i≠j）

样本熵定义为

当N取有限值时，上述得出的是样本熵估计值，为

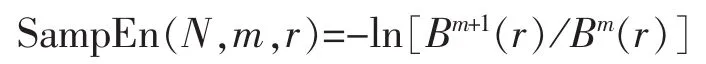
在经典二阶系统稳定性分析中，采用超调量和调节时间等性能指标来反映系统稳定性能的强弱。在一定时间范围内，超调量越小，调节时间越短，即系统各个负荷节点接受相同的扰动后能恢复稳态的时间越小，那么此负荷节点也越容易稳定，属于强节点［18］。同理用样本熵理论可这样描述：在相同时间内如该系统发出的平均信息量越大，即样本熵越大，超调量越大，调节时间越长，那么此负荷节点稳定性能越差，属于弱节点。下面以3个性质相似的波动信息来说明样本熵可以有效度量信号稳定的程度。

3 二阶阶跃响应信号分析

系统特征根的实部离虚轴越远，则其所代表的系统更稳定，稳定性能更强，不容易失稳。

图1 典型阶跃响应曲线

式（6）中s为复数变量。图1中纵坐标为响应的幅值，横坐标为仿真时间［7］。其中X是式（6）系统1的阶跃响应，Y是式（6）系统2的阶跃响应，Z是式（6）系统3的阶跃响应。

对各系统分别进行样本熵分析，由于以上系统响应在2 s时已大致稳定，采样时间为0.01 s，N为200，m取为2，r为0.25倍的标准差。得出各系统的熵值见表1所示。可得系统3比系统1、2更稳定。由经典稳定性理论知，系统3的闭环极点在系统1、2闭环极点的左边，所以系统3比系统1、2更稳定。这也验证了样本熵能很好区分系统稳定性能的强弱。

在电力系统的分析中，大部分实际电网各节点稳定程度即稳定裕度都是很大的，即使受到较大的冲击负荷扰动，系统也基本不会失稳。把样本熵理论引入到电网电压稳定性能评估的分析中，样本熵越小，说明此节点的稳定性能越好，样本熵越大则相反，因此样本熵理论可以用于评估电力系统节点电压稳定性能的强弱。

表1 特征根以及样本熵值

4 算例分析

以2010年冬季山东电网孤网运行方式为例验证了样本熵理论应用于电网稳定性能评估的有效性。联络线功率波动以及AGC的调节具体参见文献［18］。

4.1 算例仿真分析

在2010年冬季山东电网孤网运行方式下，用山东电网整个大区域进行算例仿真分析。以山东淄博受电区域的节点结果展示为例，说明运用波动强度和样本熵理论确定电网薄弱节点的方法。为进行仿真，需要建立等值模型进行简化计算。图2中淄博地区负荷节点都用三绕组变压器与电网主节点关联，橘黄色线路为500 kV主干线路。

图2 淄博受电区域

利用电力系统仿真软件，以原山东电网全网各负荷节点的功率因数增冲击负荷仿真电网各节点的电压波动情况，采用文献［7］和文献［18］的仿真模型进行分析。为了模拟扰动，假定负荷扰动成Weibull分布的形式，Weibull分布具体见文献［17］。仿真时，各负荷节点按正常运行方式运行到1s，突然对全网以Weibull分布的形式增有功和无功冲击负荷，运行到11s结束负荷扰动，运行到41s结束仿真，仿真结果见图3。

图3 淄博受电区域部分节点的电压幅值序列曲线

4.2 确定分析数据序列的长度

若序列长度过短会使数值出现偏差，遗漏有用信息，过长则会增加计算量。利用波动强度可以表征信号序列波动程度的特点，通过对仿真得到的按Weibull分布递增负荷的电压幅值波动曲线分别计算每一时段的波动强度，可得各负荷节点的波动强度曲线，如图4。可知，所有的负荷节点波动曲线在第27个时段基本维持平稳，所以每个负荷节点第27个时段以前的序列即为最佳的分析时间序列。这既保证了信息的有效性，又避免了冗余信息，减少了计算量，节约了计算时间。

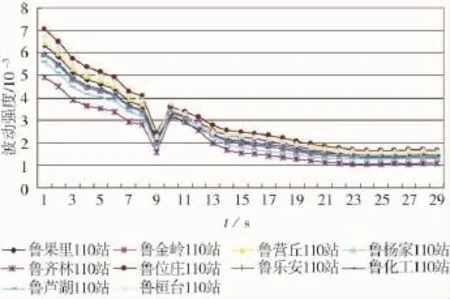
图4 淄博受电区域各节点的波动强度序列曲线

4.3 利用样本熵评估负荷节点的薄弱程度

通过对采样数据进行重构相空间分析，延迟时间取值在2.193~2.443 s之间，并通过Cao氏法计算得出的嵌入维数为5，由于采样时间间隔为0.001 s，直接进行样本熵计算容易陷入维数灾难，因此利用动力学平坦因子理论提取每个时段的平坦因子值，在此基础上运用样本熵理论进行计算，m为2，得出的淄博地区的负荷节点各样本熵值如表2所示。

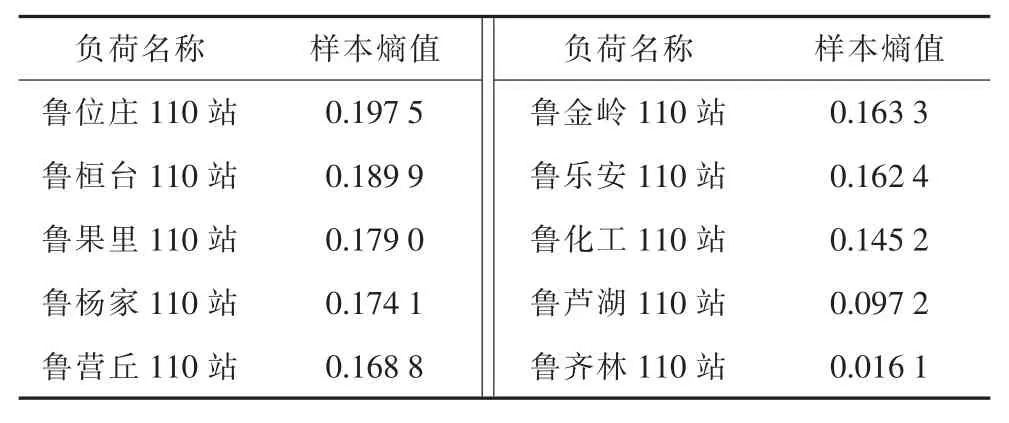
表2 淄博地区各负荷节点样本熵值

由表2可见，淄博地区鲁位庄站样本熵值最大，说明位庄站在淄博地区属于电压稳定性能的薄弱节点；相反淄博地区的鲁齐林站样本熵值最小，说明齐林在淄博地区属于电压稳定性能较好的节点，即强节点。其次鲁化工110站和鲁营丘110站样本熵值较小，为较强节点。由图4和表2可知，鲁齐林110站在开始的时段平坦因子明显比鲁位庄110站和鲁桓台110站小，即在相同的信号时段内鲁齐林110站比鲁位庄110站波动小，反映在经典稳定性分析理论上为超调量小，这验证了样本熵能很好进行节点电压稳定性能评估。

5 连续潮流（P-V曲线）法和戴维南等效法

利用传统静态分析方法中的连续潮流法［3-4］和戴维南等效法［1，4，19］来验证确定薄弱节点方法的有效性。

5.1 戴维南等效法

电网在某一潮流断面下除独立发电节点之外的任意中间联络节点或末端负荷节点，都可等效为如图5所示的简单两节点系统。

图5中Eeq∠δeq为等效电源电势，Zeq∠α=R+jX为等效阻抗，Ui∠δi为节点实际电压，SLi∠Φi=PLi+jQLi为节点等效传输功率（或等效负荷），表示按照有功流向从节点i流入的功率总和［2，19］。不同于节点直接对地意义上的戴维南等值，所以是有区别的。

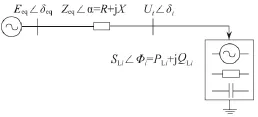
图5 戴维南等效两节点系统

采用戴维南等效法将辛安站和廉州站统一等值为华北平衡机，作为平衡节点处理。银东直流部分等值为一台定出力发电机，作为PQ节点处理。在2010年冬季山东电网孤网运行大方式下，采用文献［18］的处理方法，得到2个潮流数据断面的解去求4个未知数的方程组，得各节点戴维南等效参数，具体见文献［21］。采用的4个具体指标见文献［1，2，20，22］，得到的分析结果如表3所示。

表3 淄博地区负荷节点的各裕度指标

5.2 连续潮流（P-V曲线）法

式中：x为系统的状态变量向量，即所有母线的电压幅值和相角；λ为负荷参数。

对整个山东电网受电地区负荷保持功率因数同比增长的同时，采用文献［18］的处理方式，采用3种方式考察淄博受电区域的极限输送能力，并对3种临界电压跌落均值的计算结果取平均值，结果如表4所示。

对比表2~4可知，传统静态分析结果表明位庄站和桓台站都是弱节点，与样本熵结果基本一致。薄弱节点在样本熵计算方式下与戴维南等效方式结算结果有些不同，但是与P-V曲线法相比结果基本一致。这是由于样本熵考虑了发电机、励磁、调速系统和各种负荷模型，而传统静态电压分析没有考虑各种元件的详细模型，特别是负荷模型的影响，所以两种计算有所偏差，但是大体趋势基本一致。齐林站为淄博受电区域的强节点，由图2的受电区域图可知，这是由于齐林站紧邻500 kV输电线路主网架，离电源的电气距离较近。用传统静态分析方法（戴维南等效法和连续潮流法）也验证了本文方法的有效性。

6 结语

根据经典控制理论，借鉴系统的超调量和调节时间等性能指标，在波动强度和平坦因子理论的基础上提取分时段的平坦因子信息并结合样本熵理论，提出确定电网中电压稳定薄弱节点的方法。在山东电网2010年冬季典型运行方式下利用电力系统仿真软件得到负荷扰动按Weibull分布时淄博受电区域各负荷节点的电压幅值变化情况，利用波动强度理论和样本熵理论确定了电网薄弱节点。

本方法是离线电压稳定性能评估，分析在当前潮流断面下电网各节点电压稳定性能的强弱，与故障方式下进行电网电压稳定分析是有区别的。该方法可为电网的运行与规划提供参考。

［1］柳焯．基于节点阻抗解析的电压稳定性预估［J］．中国电机工程学报，1999，19（11）：64-68．

［2］刘道伟，韩学山，王勇，等．在线电力系统静态稳定域的研究及其应用［J］．中国电机工程学报，2009，29（34）：42-49．

［3］赵晋泉，黄文英，方朝雄，等．福建电网在线电压稳定监视与控制系统（VSMC）［J］．电力系统自动化，2007，31（14）：102-106．

［4］赵晋泉，王毅，李可文，等．一种基于连续潮流的在线静态稳定综合评估方法［J］．电力系统自动化，2010，34（4）：18-22．

［5］段献忠，何仰赞，陈德树.论电力系统电压稳定几种实用判据和安全指标［J］．电力系统自动化，1994，18（9）：36-41.

［6］王锡凡，方万良，杜正春．现代电力系统［M］．北京：科学出版社，2003．

［7］张学清，梁军，刘道伟，等.基于信号能量综合指数的电网电压稳定性能研究［J］.电力系统保护与控制，2012，40（12）：88-94.

［8］LEE B，AJJARAPU V.Period-doubling route to chaos in an electrical power systems［J］.IEE Proceedings-Generation，Transmission and Distribution，1993，140（6）：490-496.

［9］尤勇，盛万兴，王孙安.一种新型短期负荷预测模型的研究及应用［J］.中国电机工程学报，2002，22（9）：15-18.

［10］何正友，蔡玉梅，钱清泉.小波熵理论及其在电力系统故障检测中的应用研究［J］.中国电机工程学报，2005，25（5）：38-43.

［11］Lerro D，Bar Shalom Y.Tracking with debiased consistent con verted measurement versus EKF［J］.IEEE Transactions on Aerospace and Electronic Systems，1993，9（3）：1 015-1 022.

［12］段献忠，何仰赞，陈德树.论电力系统电压稳定几种实用判据和安全指标［J］.电力系统自动化，1994，18（9）：36-41.

［13］葛家怡，周鹏，赵欣，等.睡眠脑电时间序列的非线性样本熵研究［J］.电子器件，2008，31（3）：972-974.

［14］彭涛，陈晓宏，庄承彬.基于样本熵的东江月径流序列复杂性分析［J］.生态环境学报，2009，18（4）：1 379-1 382.

［15］王燕萍，顾卫国，张红霞，等.CTAC减阻流体湍流高阶矩的研究［J］.节能技术，2007，25（141）：10-13.

［16］李红智，罗毓珊，王海军，等.圆弧型与X型开缝翅片空气侧流动与传热特可视化试验［J］.化工学报，2008，59（8）：1936-1941.

［17］Takens F.Detecting strange attractors in turbulence［J］.Lecture Notes in Math，1981，898（8）：366-381.

［18］张学清，梁军，董晓明.基于累积指数的电网电压稳定性能的评估［J］.电工技术学报，2012，27（7）：235-241.

［19］Cao H J，Jing Z J.Chaotic dynamics of Josephson equation driven by constant DC and AC forcings［J］.Chaos，Solitons&Fractals，2001（12）：1 887-1 895.

［20］John Hetzer，David C.Yu，Kalu Bhattarai.An Economic Dispatch Model Incorporating Wind Power［J］.IEEE Transactions on Energy Conversion.2008，23（2）：603-611.

［21］汪洋，卢继平，李文沅，等.基于局部网络电压相量的等效模型及其电压稳定性指标［J］.中国电机工程学报，2008，28（34）：52-59.

［22］汤涌，孙华东，易俊，等.基于全微分的戴维南等效参数跟踪算法［J］.中国电机工程学报，2009，29（13）：48-53.

［23］Corsi S，Taranto G N.A Real-time Voltage Instability Identification Algorithm Based on Local Phasor Measurements［J］.IEEE Transactions on Power Systems，2008，23（3）：1 271-1 279.

Research on Voltage Stability Performance of Power Grid Based on Sample Entropy

YIN Maolin，ZHANG Xueqing，SHI Dongming，LIN Shan，ZHANG Yuting，XING Hua，JIANG Peng
（State Grid Jinan Power Supply Company，Jinan 250061，China）

In order to assess the voltage stability weak node of power grid，a method of voltage stability analysis based on sample entropy was proposed.Firstly，the voltage amplitude information of power grid was obtained using the PSSE dynamic simulation software.Secondly，the optimal length of the sequence required was determined for stability analysis by the fluctuation intensity theory of kinetics.Thirdly，the voltage amplitude information was extracted by applying the theory about flatness factor on power engineering when the voltage amplitude signal had been received，thus，the weak node of voltage stability in power system was conformed on the basis of sample entropy theory.Finally，the proposed method was effectively validated by the static voltage analysis of the Thevenin equivalent theory，continuation power flow and operation mode data for the winter of 2010 in Shandong power grid，and it could provide a useful reference on operation and planning for power grid.

power grid；fluctuation intensity；voltage stability；sample entropy

TM712

A

1007－9904（2015）05－0023－05

2015-02-09

尹茂林（1964），男，工程师，主要研究方向为电力系统运行与控制；张学清（1982），男，工程师，主要研究方向为电力系统运行与控制。