高精度多频脉冲超声测距法研究

吴 军,沈梦婷

(天津大学精密测试技术及仪器国家重点实验室,天津300072)

高精度多频脉冲超声测距法研究

吴 军,沈梦婷

(天津大学精密测试技术及仪器国家重点实验室,天津300072)

传统的超声测距方法基于单频脉冲飞行时间,原理简单、应用灵活,但由于声波易受空气衰减以及电路噪声影响,其测量精度较低,多频连续波相位检测法可以达到较高的精度,但其受限于连续声波发射,应用范围较小。为兼顾测量精度与应用范围,提出一种采用多频超声脉冲发射的方法,利用各频段声波之间的固有时间差值,结合飞行时间法精确估计超声脉冲的到达时间,再通过温度补偿测量现场的声速,即可得到精确的被测距离。该方法能够拓展超声测距的应用范围,简化硬件设计,经实验验证,在3 m范围内,测量精度可以达到0.3 mm左右。

超声测距;多频脉冲;飞行时间;时差估计;温度补偿;最小二乘拟合

1 概述

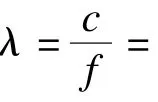
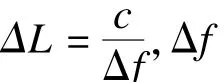
本文提出一种多频脉冲超声波测量飞行时间的算法。发射2组频率相近的超声波,对于同一距离,不同频率的接收/发射的相位偏移之差恒定,根据此原理,判断出接收波起振时间,实现大测量范围的高精度测量。

2 飞行时间精测法

本文选择了震荡特性较好的静电式超声探头,中心频率为50 kHz。发射端与接收端分离的对射式结构,发射8个频率为f1(f1=50 kHz)的脉冲,间隔1ms发射8个频率为f2(f2=51.56 kHz)的脉冲。将接收波通过正弦检波转变为方波。f1(f2)发射波发射时刻开始计时,检测到接收波第n个上升沿的时间t1n(t2n)。

在理想情况下,接收波通过比较电路没有漏检的周期,发射/接收波模型如图1所示,则不同频率接收波之间存在的对应关系如图2所示,满足:

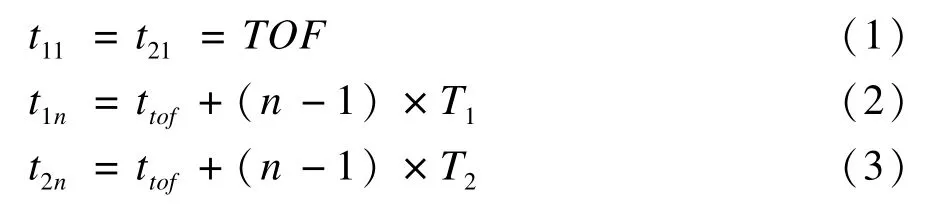
其中,ttof为超声波从发射端传播到接收端的飞行时间。

图1 2组频率相近的超声波发射/接收理想模型

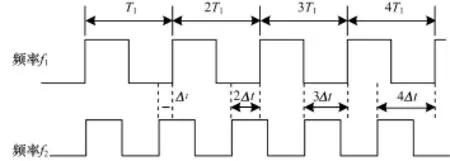
图2 不同频率接收波之间的关系

根据式(2)、式(3),得:

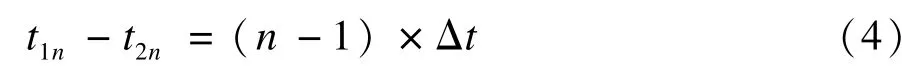
其中,Δt=T1-T2,有:

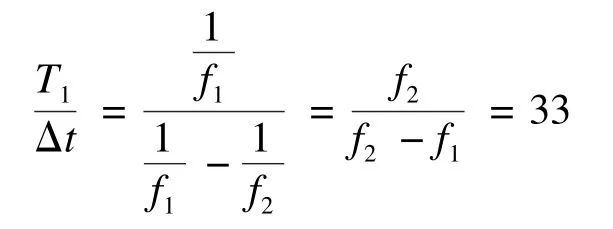
故t1n-t2n＜＜T1(发射波是8个周期的脉冲,可知n≤8)。

式(4)表明了不同频率接收波对应的上升沿之间时间的关系。

但在实际情况中,无论是阈值可变法、可控增益法,都无法保证接收波没有漏检的周期,且漏检的周期数会随着传播距离的增加而增加,因为声波在空气中传播呈指数衰减。要想提高测距精度,必须准确判断接收波漏检的周期数。

f1接收波、f2接收波均有检漏的周期,且周期数不定。假设f1漏检m1个周期,f2漏检m2个周期,将式(2)、式(3)转换为实际模型,得到:

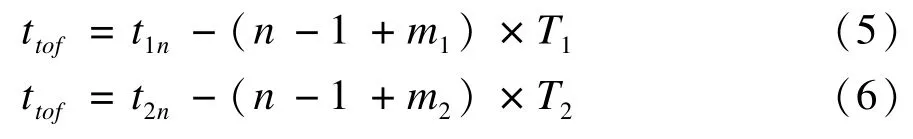
令Δm=m1-m2,则2组接收波之间存在下列关系:

(1)Δm≥0,有:

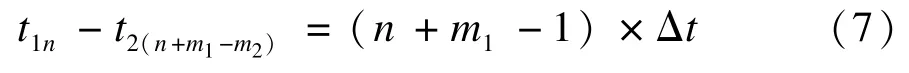
其中,t1n,t2(n+m1-m2)对应实际波形中到第n+m1个上升沿的时间。

(2)Δm＜0,有:

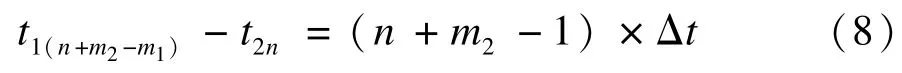
其中,t1(n+m2+m1),t2n对应实际波形中到第n+m2个上升沿的时间。

通过判断出Δm的值,将t1n,t2(n+m1-m2)或t1(n+m2+m1),t2n对应上,即可求出对应的m1,m2的值。

以n=2,m1=4,m2=2为例,如图3所示。Δm=2＞0,根据式(5),t12-t24=5×Δt。

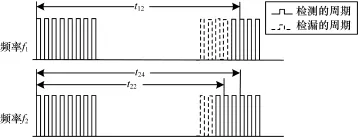
图3 2组不同频率超声波发射/接收实际模型

Δm的判断方法如图4所示。检测t1i,t2j(初始时i=j=1)并比较大小,当t1i＜t1j时,m1＜m2,f1漏检的周期数小于f2漏检的周期数,则增加i直到t1i≥t1j;

当t1i≥t1j时,m1≥m2,此时判断t1i-t2j与T1的大小。

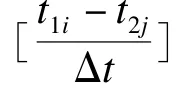
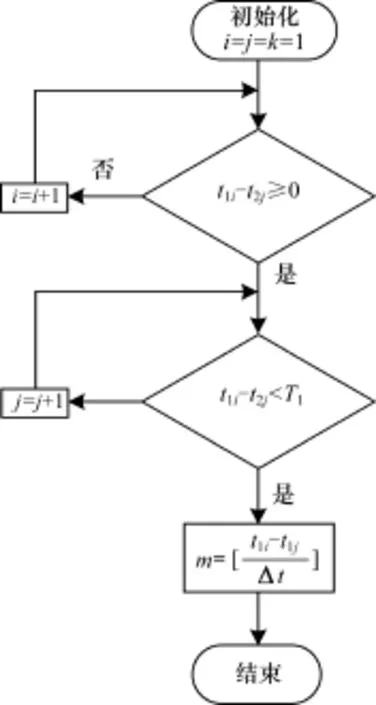
图4 漏检周期差Δm判断流程

3 温度补偿

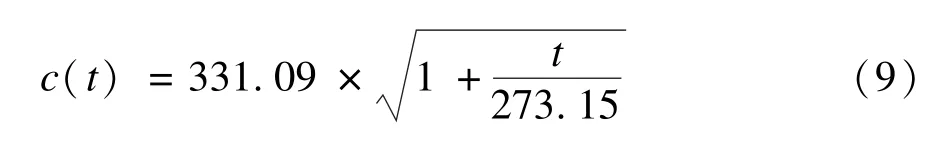
4 软件实现

系统的软件模块流程如图5所示。系统初始化后,清空计数器,然后初始化数字频率合成器DDS生成频率为f1,f2的超声波。依次发射8个周期的f1,f2脉冲,发射的同时开始计时。记录到接收波f1,f2每个上升沿的时间t1n,t2n(n=1,2,…,8)。根据图4的流程图判断Δm,从温度模块实时测量温度T,将m1,m2,T传输给上位机,根据式(5)、式(6)、式(9)得到距离L。

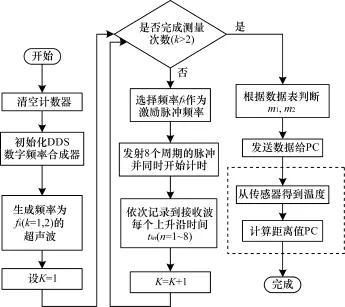
图5 系统的软件模块流程

5 实验与分析

多频时间法有2个关键:(1)对2个频率的接收波漏检周期数m1,m2的判断;(2)接收波频率的精度,根据式(5)、式(6),漏检部分实际的周期与驱动信号的周期T1或T2的偏差,将直接影响起振时间的判断。实验1是对m1,m2的判断,实验2是对测量距离的误差分析。实验状态如表1所示。其中,测量距离真值、m1真值、m2真值是用示波器测量起振时间标定的,温度使用精密温度计测量。实验装置示意图如图6所示。

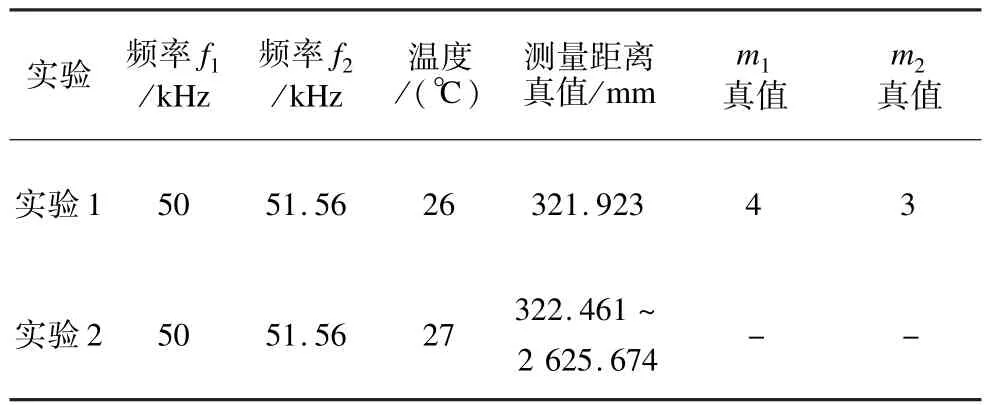
表1 实验状态

图6 实验装置示意图

5.1 m1,m2的判断

在实验1的状态下,得到数据表2。根据图4的流程,判断出Δm=j-i=1,可计算出m的值。为了保证m值的准确性,使i=i+1,j=j+1,多次计算得到序列Mk。t1i,t2j实际对应情况及Mk值如表3所示。

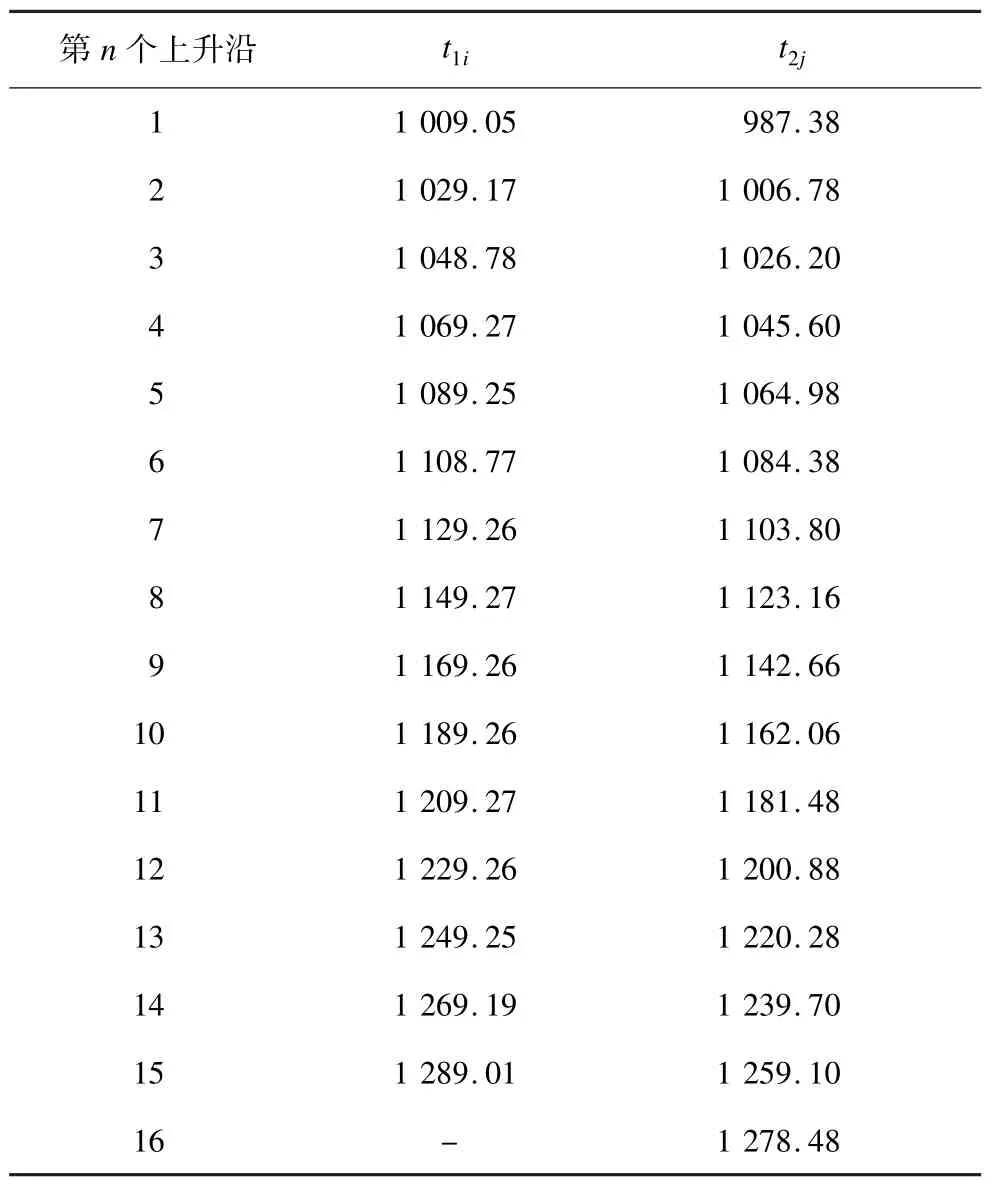
表2 判断m值的实验数据

表3 判断m值的实验调整数据

将Mk序列线性拟合,得到拟合曲线方程y=p1×x+p2,p1=1.033 5,p2=2.760 5。其中,截距p2取整[p2]=3=m1-1,得到m1=4。Mk拟合曲线如图7所示。

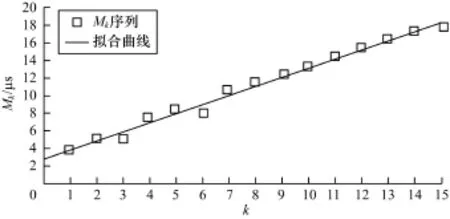
图7 Mk序列拟合曲线

5.2 测量距离误差分析

在实验2的实验状态下,在322.461mm～2 625.674 mm范围内,每隔120 mm测量一次,得到相应的m1,m2。根据式(5)、式(6)得到飞行时间继而得到距离值,如图8所示。其中,d1表示代入式(5)即根据频率f1得到飞行时间,d2表示代入式(6)即根据频率f2得到飞行时间。图9为对应2种方式得到的测量结果与真值的误差。由图可知,根据频率f1(f1=50 kHz即中心频率)得到的测量结果误差明显较小。

图8 2种方式测量结果比较

图9 2种方式测量误差比较

6 结束语

本文在飞行时间测距法的原理基础上提出了一种新的高精度超声测距法。针对飞行时间法存在的声衰减导致起振时间测量不准确的问题,根据不同频率的接收/发射的相位偏移之差恒定的原理判断起振时间。本文通过发送2种不同频率的驱动信号,分析接收波之间存在的相对关系,建立发射波/接收波实际模型,判断2组接收波漏检周期数,进而得到准确的飞行时间。

[1] 叶宝玉,王钦若,熊建斌,等.基于超声波的模型船舶室内定位系统研究[J].计算机工程,2012,38(19): 258-260,265.

[2] Medina C,Segura J C,de la Torre A.Ultrasound Indoor Positioning System Based on a Low-power Wireless Sensor Network Providing Sub-centimeter Accuracy[J]. Sensors,2013,13(3):3501-3526.

[3] 任晓奎,郭海雯.基于超声波和GPS技术的车辆防碰预警系统[J].计算机测量与控制,2013,21(3): 694-696.

[4] 安葳鹏,李长青.超声波汽车追尾仪的研究[J].计算机工程,2001,27(1):189-190.

[5] 王荣扬,钱振华,殷勇辉.基于FPGA的互相关无串扰超声测距系统[J].计算机工程,2013,39(8):307-313.

[6] 戴华平,胡红亮.基于耦合同步混沌系统的超声波测距方法[J].计算机工程,2013,39(5):23-27.

[7] 陈 建,孙晓颖.一种高精度超声波到达时刻的检测方法[J].仪器仪表学报,2013,33(11):2422-2428.

[8] 张攀峰,王玉萍.带有温度补偿的超声波测距仪的设计[J].计算机测量与控制,2012,20(6):1717-1719.

[9] 曾祥进,王 敏,黄心汉.自动增益电路在超声波测距系统中的应用研究[J].测控技术,2005,24(7):69-71.

[10] Kimura T.AHighResolutionUltrasonicRange Measurement Method Using Double Frequencies and PhaseDetection[C]//ProceedingsoftheIEEE Ultrasonics Symposium.Settle,USA:IEEE Press,1995: 737-741.

[11] Huang K N,Huang Yupei.Multiple-frequency UltrasonicDistanceMeasurementUsingDirectDigital Frequency Synthesizers[J].Sensors and Actuators A: Physical,2009,149(1):42-50.

[12] Huang C,Young M,Li Y.Multiple-frequency Continuous Wave Ultrasonic System for Accurate Distance Measurement[J].Review of Scientific Instruments, 1999,70(2):1452-1458.

[13] Huang Y,Young M S.An Accurate Ultrasonic Distance Measurement System with Self Temperature Compensation[J].Instrumentation Science and Technology, 2009,37(1):124-133.

编辑 顾逸斐

Study on High Accurate Ultrasonic Ranging Method Using Multi-frequency Pulse

WU Jun,SHEN Mengting
(State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China)

The traditional ultrasonic ranging method is based on time of flight using single frequency pulse.It is flexible in application but has low accuracy.Another high accurate method is based on multi-frequency continuous wave;however its application is limited by the continuous sound wave.In order to consider both measurement accuracy and application, this paper presents a novel method by using multi-frequency ultrasonic pulse.This method obtains accurate distance based on the sound velocity which is compensated by temperature and accurate time of flight estimated through the inherence time difference of different frequency pluses.Experimental results prove the measurement accuracy can achieve about 0.3 mm for the distance up to 3 m.

ultrasonic ranging;multi-frequency pulse;time of flight;time difference estimation;temperature compensation;least-squares fitting

吴 军,沈梦婷.高精度多频脉冲超声测距法研究[J].计算机工程,2015,41(2):278-281,286.

英文引用格式:Wu Jun,Shen Mengting.Study on High Accurate Ultrasonic Ranging Method Using Multi-frequency Pulse[J].Computer Engineering,2015,41(2):278-281,286.

1000-3428(2015)02-0278-04

:A

:TP39

10.3969/j.issn.1000-3428.2015.02.053

国家“863”计划基金资助项目(2012AA041205);国家自然科学基金资助项目(51305297)。

吴 军(1986-),男,博士研究生,主研方向:超声定位系统;沈梦婷,硕士研究生。

2014-02-24

:2014-03-20E-mail:wujun8686@tju.edu.cn