半监督空间化竞争聚集算法及其在图像分割中的应用

于 平,王士同

(江南大学数字媒体学院,江苏无锡214122)

半监督空间化竞争聚集算法及其在图像分割中的应用

于 平,王士同

(江南大学数字媒体学院,江苏无锡214122)

经典竞争聚集(CA)算法在聚类时对于样本中的少量已知信息没有加以利用,但这些信息往往需要应用到整个聚类过程中。此外,在相似度度量函数的选择上CA算法使用常见的欧氏距离,然而欧氏距离仅适用于团状数据,制约了算法的应用范围。针对上述问题,通过引入具备半监督学习能力的半监督项对隶属度矩阵进行增强,利用聚类中心和中心邻近的点组成空间,把样本点与该空间的距离替代欧氏距离作为新的相似度度量标准,并给出判断聚类中心能否合并的阈值参数,最终得到半监督空间化CA算法。通过在人造图像和真实图像上的分割结果表明,该算法能够更准确地获取聚类类别数以及更好的聚类效果。

竞争聚集算法;相似度度量函数;欧氏距离;半监督;空间距离;阈值参数

1 概述

聚类是模式分类和系统建模的基本方法[1]。它根据样本个体之间的相似性把样本空间划分为不同的子集。聚类后的样本,同一个子集空间中的个体具有尽可能大的相似度,而不同子集空间中的个体差别较大。

本文针对当前竞争聚集(Competitive Agglomeration,CA)算法存在的问题,提出一种新的CA聚类算法,称为半监督空间化CA算法。该算法通过构造半监督学习项有效地对待聚类的样本数据通常存在的少量有益信息加以利用,从而增强聚类效果。此外,为解决欧氏距离所造成的缺陷,提出利用聚类中心和中心邻近的点组成空间,把样本点与该空间的距离替代欧氏距离作为新的相似度度量标准,增强算法的适用性。所采用的空间距离由于考虑了数据的结构和方向信息,其抗噪音性能更佳,提高了算法的抗噪能力。给出一种合适的判断聚类中心合并的阈值参数,对最终聚类个数进行有效调控,为算法获取更为精准的类别数提供保障。

2 背景介绍

目前常用的聚类方法主要分为2大类[2]:层次聚类算法和目标函数聚类算法。经分析这2类算法各有优缺点,可总结如下:(1)层次聚类算法是产生一个聚类层级即聚类树的非单一聚类,主要通过合并和分裂2种方式来实现。该类算法不受初始化和局部极小值对于聚类结果的影响,不用提前设置聚类得到的类别总数,且算法结构较为明朗。但该类算法不适用大的数据集,初始化阶段某层出现的错误将在合并和分裂过程中向下一层延续,并最终影响全局的聚类。(2)基于目标函数的聚类算法,这类算法可以把握数据整体的结构和形状,它由具备类别特征的原型来代表一个类别,由特征矢量到类别原型的距离和作为目标函数,通过迭代不断减小目标函数,当目标函数取得极值时结束算法。该类算法可以分为硬聚类和软聚类2种[3]。2种算法的不同主要表现在对于隶属度的取值方面。硬聚类的隶属度值为0或者1,软聚类的隶属度值为一个模糊的区间[0,1]。软聚类由于其模糊性成为聚类分析的主流,以文献[4]提出、文献[5]推广的模糊C-均值聚类(Fuzzy C Means clustering,FCM)最为经典。该算法的动态迭代使算法可以不断更新数据对于类别的隶属关系,使算法的错误不会固定延续,但这同样带来了需要更大内存存储空间和更大计算量的问题。且FCM算法执行前需要预判和设定聚类对象的类别总数、初始化,这2项参数决定了最终的聚类效果,即决定了算法能否得到最佳的聚类类别数目和目标函数能否取得全局极值。这也是FCM算法及其他相似的迭代聚类算法所面临的共同问题。

为解决上述问题,文献[3]提出了一种新颖的聚类算法,即竞争聚集(CA)算法。该算法采用层次聚类的初始化方式,使算法不受初始化和局部极小值的影响,用目标函数聚类的特点来避免层次聚类中的缺陷。此外,其更可以通过迭代的方式自动寻找到待聚类样本数据集最佳的聚类类别数目,是一种无监督的聚类方法。尽管CA算法表现出了一些独特的聚类性能,并且在数据处理[3]、遥感卫星图像处理[6]和图像分割[7]等领域得到了广泛的应用。但是,经研究发现,当前的CA算法在聚类时忽略了待聚类样本数据所包含的一些有益的已知信息,而这些有益信息往往能够对最终的聚类结果起到正面作用。此外,经典的CA算法在相似度度量函数的选择上使用了最常见的欧氏距离,然而欧氏距离仅适用于团状数据,制约了算法的应用范围。

3 CA算法

CA算法是在层次聚类和目标函数聚类的基础上提出的方法。它通常以远大于样本类别总数的小簇来初始化,然后在迭代过程中通过偏移项的作用,不断增加真实聚类中心的竞争力,削弱虚假中心的影响,直至满足算法的终止条件,从而得到合适的聚类效果。

3.1 CA算法基本原理

设X={x1,x2,…,xN}是数据样本空间,B=(v1,v2,…,vC)是数据集的聚类中心集合,则CA算法的目标函数可以表示为:

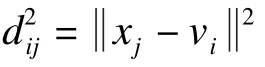
式(1)可以看作2个部分,第1部分与模糊指数m=2时的FCM目标函数功能相似,用来确定聚类簇的大小和形状。第2部分是一个偏移项,用来寻找最佳的聚类类别总数。

偏移项中参数:

其中,k表示算法迭代的次数;η0和τ是固定的取值。

文献[3]中根据拉格朗日条件极值的求解方式给出了式(1)取得极值时参数矩阵U和B的值。

在式(2)的约束下,隶属度的值为:

式(5)是式(1)中FCM部分的隶属度更新,式(6)是偏移项部分的隶属度更新。

式(6)中Ni表示第i类的基数;表示类别基数的加权平均,更新公式如下:

同理得到的聚类中心为:

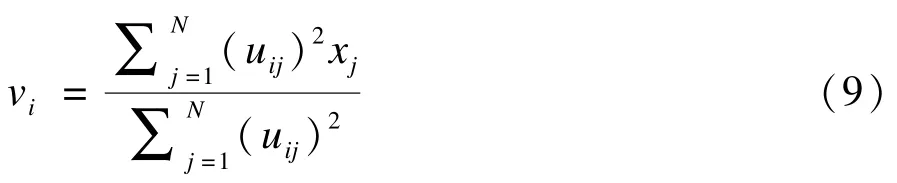
根据求解得到的参数公式,只要给CA算法聚类样本,算法就可以通过迭代,得到最佳的划分结果。

3.2 CA算法存在的问题

CA算法通过迭代过程中不断丢弃虚假中心的方式可以自动得到最终的聚类数目,在处理某些数据时存在其可取性,但从现实生活中的数据特点来考虑,CA算法在某些方面尚存在某些问题。这可以分为2个方面:

(1)样本信息利用率不高。实际生产和生活中的数据,一般情况是建立在少数已知信息的基础上的。无监督的CA算法,极大地浪费了这些稀少却对数据聚类十分有用的信息,这必将影响最终聚类结果的恰当程度。

(2)相似度度量标准并不可靠,CA算法的目标函数使用欧氏距离作为相似度度量函数。欧氏距离虽然在计算上简单方便,但仅适用于团状的数据聚类,在处理其他结构的聚类时存在偏差,而且,将目标函数最小化来得到最佳聚类结果的方法存在对数据集进行均等划分的可能[8-9],此外,欧氏距离本身的抗噪能力也不令人满意[10]。

以上问题,制约了CA算法的适用性范围。本文将提出一种新的改进CA算法来解决上述问题,增强算法的性能及适用性。

4 半监督空间化CA算法

针对前一节CA算法所存在的问题,本节提出一种新的改进CA算法。该算法通过引入半监督学习方法改进了目标函数,此外为了增强适用性进一步采用了空间化距离度量标准改进原本的欧氏距离,最终得到了半监督空间化CA算法。

4.1 半监督方法

针对样本信息利用率不高的问题,本文通过对隶属度引入已知信息的方式,使其充分利用少量但重要的信息,提高聚类结果的正确率。解决方法如下[11]:

待聚类的数据集可以写为已知和未知数据组成的形式:

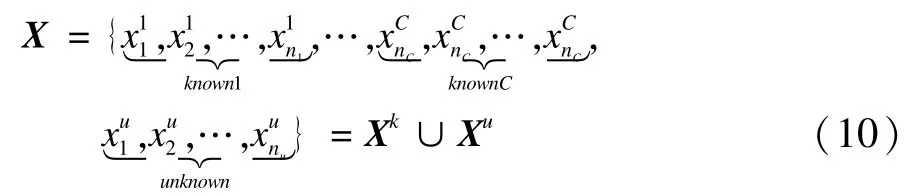
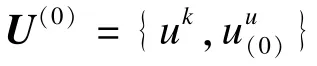
4.2 空间距离的原理

针对3.2节中提到的欧氏距离仅适用于球状聚类且存在等划分趋势的缺陷,本文使用了将欧氏距离空间化[12]的方法进行修正和改进。

图1中Mi代表样本的所有可能聚类中心所组成的平滑流形,Ni是距离待测样本sq最近的聚类中心i和中心i邻近点的集合,xi1和xi2代表Ni中第i类聚类中心和第i类中心邻近的2个点,Si是Ni限定的子空间平面,那么通过其他可能的聚类中心和它们邻近点的平滑流形也必然与Si相交[12]。当Ni基数为2时,xi1和xi2是距离sq最近的点。

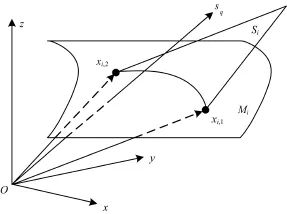
图1 空间距离原理推导

那么sq是距离子空间Si最近的点,则距离为:

式(12)的距离在图1中是一个通过原点的平面,考虑到逐个计算式(12)中欧氏距离的复杂性,可以直接把子空间Si看作一个整体来计算。

设Ni是xi的点组成的矩阵且满足列满秩条件,该平行体的体积[13]:

与式(13)类似,若sq和Ni线性无关,那么它们共同组成的超平形体的体积为:

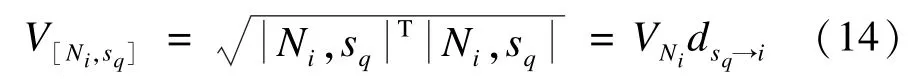
根据上式,则式(12)的距离可以改写为:

图2中“oabcdefg”表示xj和矩阵Vi所组成的平行六面体[12],体积是“og”与平行四边形“oabc”的距离和该“oabc”面积的乘积,将“og”和“oabc”表示的量和空间分别用xj和Vi表示,那么根据式(15)“og”到“oabc”所组成的空间距离的平方可以表示为:

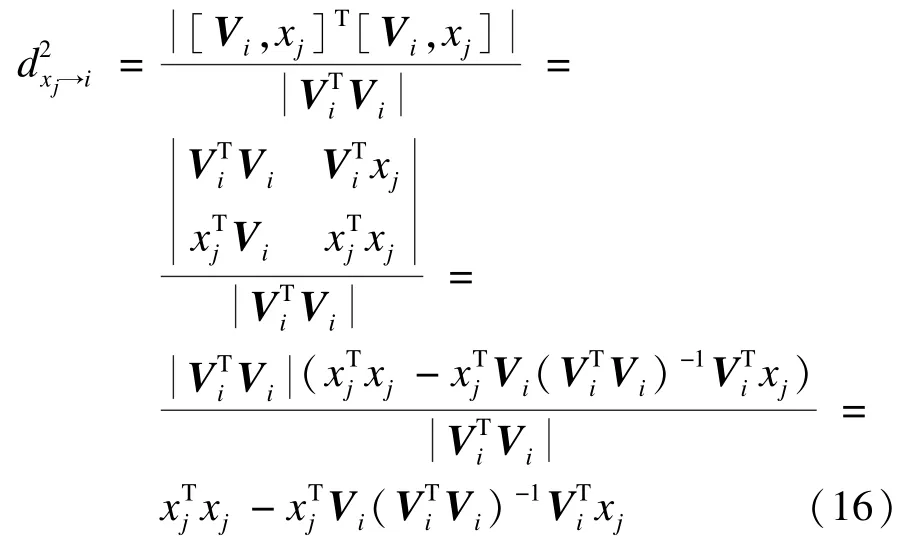
将式(16)应用到聚类算法中,其中,xj表示样本中第j个点;Vi是第i个中心点和中心邻近点所组成的矩阵,那么dxj→i就可以表示xj到Vi组成的超平行体的距离。存在的条件是保证矩阵Vi的列向量线性无关,为了满足这个条件,将式(16)正则化[14]得:

图2 空间距离推导

由于在式(16)中

观察式(17),可以发现该式类似于大量的核学习方式,同样可以进行核化得到核化后的距离标准。为了简洁,在本文中对于该部分将不再探讨,主要采用式(17)作为距离函数。

4.3 邻近中心点的判断与合并部分

上一节介绍了CA算法空间化距离的原理及计算方式,由这些介绍可以看出在一定范围的聚类中心对于改进后的CA算法距离差异并不大,但这些聚类中心时常却因为不满足传统CA的舍弃条件而被错误地保存下来。针对这样的状况,根据参考文献[15]的思想,加入新的判别方式来合并更新这些聚类中心,以使算法达到迭代出合理聚类总数的目的。

判断合并原理如下:

式(18)是聚类中心相似性的距离衡量方式;θ是合并聚类中心的阈值,根据实验经验在本文中取0.001;式(20)和式(21)分别为新聚类中心和它对应的隶属度的计算方法。

考虑到聚类中心集合内有3个或多个元素同时满足合并条件时,同一类的隶属度将分别被合并多次的情况,本文对更新后的隶属度重新按约束条件进行修正。

该段程序执行过程如下:

步骤1计算聚类中心集合内任意2个元素的距离。

步骤2将满足dv≤θ的聚类中心按照式(20)的方式合并为新的聚类中心,按照式(21)计算对应的新隶属度。

步骤3按照约束条件修正更新后的隶属度矩阵,更新聚类数目。

4.4 半监督空间化CA算法

根据前3节的介绍,下面给出本文所提半监督空间化CA算法的具体目标函数如下:

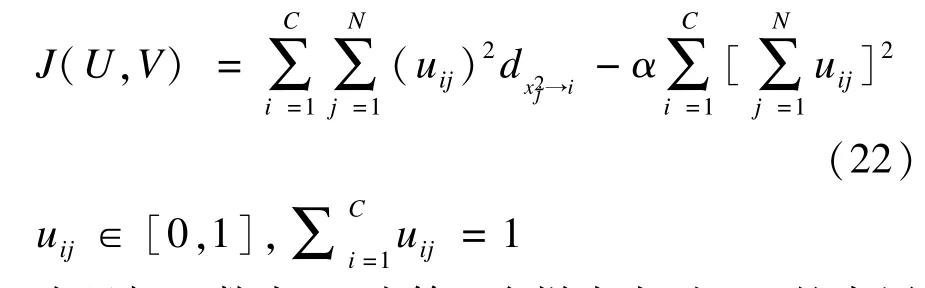
4.4.1 目标函数迭代参数的推导

为了得到最优的聚类结果,下面介绍所需迭代参数的相关推导。

(1)求解隶属度的更新公式:

根据拉格朗日极值求解方式,可将式(22)写作如下的优化函数形式:

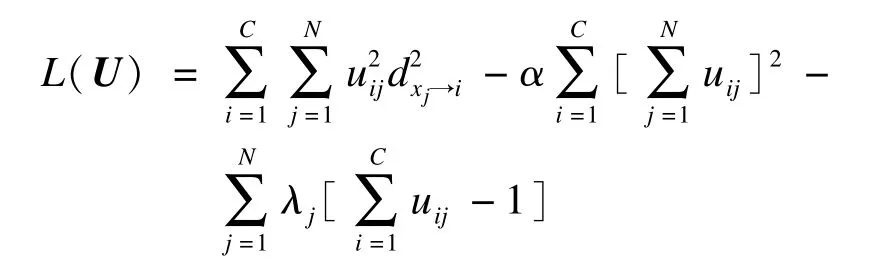
1)对uij求偏导和定义Ni:

则式(23)可化为如下形式:

将式(25)代入式(24)得到:

2)求参数λ:

把式(22)的约束条件代入式(26)两边可得:

由式(27)可以解出:

3)求解隶属度更新矩阵:

把式(28)代入式(26)可以解出:

式(29)可以写为:

在式(30)中,有:

在式(32)中,有:

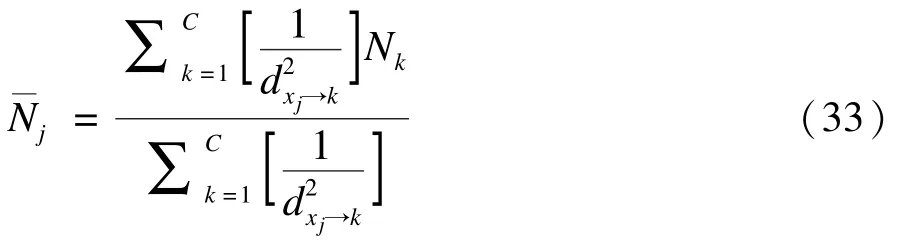
算法的参数:

其中,t为迭代的次数;τ和η0为定值。

(2)聚类中心的更新公式求解:

由于本文中所使用空间距离的原理本质仍然是欧氏距离,因此用欧氏距离近似代替该距离进行中心参数的迭代推导。

即:

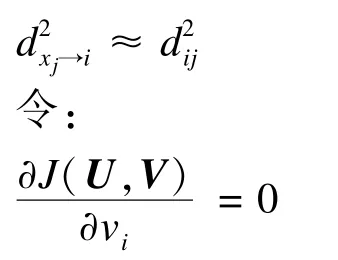
则求导后的目标函数可近似为:

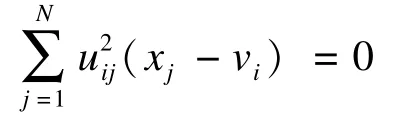
求解得到:

4.4.2 算法具体执行过程描述

根据上节推导的参数,改进后算法的具体执行过程如下:

输入待聚类的样本数据X={x1,x2,…,xN},该样本数据可以写成式(10)的形式,N表示样本空间的大小

输出样本的类别划分

初始化:设定聚类中心个数的最大数值C=Cmax,2≤Cmax≤N;初始化迭代计数t=0,给出丢弃竞争簇的判别条件ε,定值η0,τ,如式(11)利用部分已知信息,初始化隶属度矩阵U。

优化迭代:

步骤2更新计算基数矩阵Ni,判断类别基数是否满足丢弃竞争簇的条件,如果Ni＜ε,则丢弃类别i对应的元素。

步骤3利用矩阵U(t)中不满足丢弃条件的元素,根据式(35)计算更新聚类中心vi。

步骤4对更新的聚类中心进行判断合并,更新聚类中心C。

步骤5判断聚类中心的个数是否发生改变,若发生改变,则令迭代计数t=t+1,跳回步骤1依次计算;否则算法结束,跳出循环。

5 实验结果与分析

随着信息化和数字化成为时代的特征,数字图像在人类生活中扮演的角色越来越重要,对于这些图像信息处理的需要也越来越迫切。图像分割是数字图像处理的主要技术之一,图像分割的好坏将直接影响到图像的后续处理。基于图像分割重要意义,本文的实验主要将应用于图像分割领域。为验证算法的有效性,在实验部分将分别用人造图像和真实图像对所提算法进行评估。

本文设计了与相关算法进行性能的比对,其中有常用的FCM算法[4,5]、基于已知信息的可能性模糊C-均值聚类(Possibility Fuzzy C Means clustering, PFCM)算法[11]及经典CA算法[3],通过与以上3种算法的比较对本文算法的性能做出综合评价。

在人造图像的实验中,与相关算法进行性能对比时,采用归一化互信息(Normalized Mutual Information,NMI)[16-17]作为评价指标进行讨论,评价指标的定义如下rNMI:

其中,Ni,k表示第i个聚类与参考类k的契合程度;Ni表示第i个聚类所包含的数据样本量;Nk表示类k所包含的数据样本量;N表示整个数据样本的总量。

该评价指标的取值为[0,1]区间,数值越高表示聚类的性能越好。需要说明的是,对于图像分割,该评价指标只能应用于有标准图的实验,即人造图像实验,而真实图像由于缺乏标准图,并不能进行评价。对于不能评价的真实图像可以通过观察分割结果来进行评判。

实验的运行环境和相关算法的参数设定如表1和表2所示。

表1 实验环境

表2 各算法的相关参数设定

表2说明了在实验中各个算法的参数设定。一般隶属度指数定义在[1.5,2.5]之间[18],在绝大多数情况下可以直接设定为2[19]。在表2中,FCM和PFCM的模糊度指数采用经典的设定,即m=2;C是聚类中心数目,根据对人造图像和其他2幅真实图像的设定与预判,聚类总数分别设置为3类、2类和3类;M指算法迭代的最大循环次数,Q是算法迭代终止的阈值,该两项根据实验经验取值。根据文献[3]CA算法和本文算法中最初的聚类总数Cmax为15;η0和τ是算法中偏移项的参数,根据实验调试的结果3幅图像η0分别设定为1,3和2;ε是Ni的判断阈值参考文献[3]设定。

5.1 人造图像实验

为了检验本文算法的图像分割效果,选取了有明确聚类中心的人造图像。考虑到聚类结果的直观性,模拟图像的类别不宜过多,过多一则不便于观察图像效果,二来不容易体现本文算法的自动寻找类别总数的性能;模拟图像的类别太少,不能体现算法性能比对的价值;因而本文图像构建了3个类别。3类的聚类中心按顺时针方向依次为(0.117 2, 0.312 5,0.968 8),出于全面考虑,设定了2个接近的中心和一个差别较大的中心。另外,在图像中随机选取了15个点作为已知信息使用。图3为各算法对加入噪声后的图像进行聚类后生成的分割结果对比。

由图3的人造模拟图像的聚类结果可以看到, CA算法由于噪声的影响,最终所得类别总数超过了3类,与真实类别数不符,可以判定为失去自动寻找聚类总数的性能。而本文算法并未受到噪声的影响,成功获取了正确的聚类总数。另外,从图像上可以看出FCM算法与PFCM算法的聚类效果没有明显差别,而本文算法对于左侧2类的聚类效果要明显优于这2种算法。

图3 人造模拟图像的聚类结果

下面对图像聚类后得到的数据进行分析。表3为图像设定的数据和各算法处理加噪后图像得到的数据。

表3 人造图像的数据及各算法的聚类结果数据

分析表3数据可以得到,聚类中心方面,FCM算法和PFCM算法得到的聚类中心与图像的真实中心较为接近;本文算法除第2个中心较接近真实中心外,其他值存在的偏差要大于另2类算法。出现这种状况的原因可以分为2个方面:(1)本文算法采取近似的方式,用传统欧氏距离得到的中心更新公式来替代本文算法实际并不存在的中心点迭代公式; (2)本文算法采用空间化距离,把聚类中心和与它邻近的点作为一个整体来考虑,这无疑扩大了聚类中心取值的范围,算法得到的中心数值并不能完全等效传统算法意义上的聚类中心。表3中作为评价指标的归一化互信息的值是算法多次执行后取得的平均值。分析该指标可以得到,本文算法的聚类性能要稍好于其他2类算法;PFCM算法的性能对比FCM算法要差一些,根据文献[11],PFCM算法将已知信息的隶属度值取为1的做法破坏了样本原有的模糊属性,在一定程度上会对整个样本集的模糊划分造成影响。

FCM算法和PFCM算法是经过预判后设定的聚类类别数目,但是现实生活中某些图像预判类别总数并不那么容易。对于这种状况,显然本文算法更具优势。

5.2 真实图像实验

为了进一步验证本文算法处理真实图像的分割效果,选取了2组真实图像进行实验。这2组真实图像分别是自然界的常见图像和医学上的常见图像。真实图像中已知样本点总数如表4所示。

表4 真实图像的已知样本数据点数

表5是各个算法对2组图像的聚类总数,图4和图5分别是2组真实的图像和算法对它们的聚类结果。

表5 真实图像聚类后的类别总数

图4 图像1的聚类结果

图5 图像2的聚类结果

根据表5,可以看出CA算法依旧无法获取较为准确的聚类类别数,而本文算法依旧保持了较好的聚类性能,得到了正确的聚类类别数。进一步地观察图4的聚类结果,其中,PFCM算法对于目标和背景的聚类效果要优于FCM算法,而本文算法的聚类结果更优于PFCM算法,不仅聚类得到的树叶区域范围较广,而且噪点较少。这有效地验证了本文算法的聚类优势,更说明了使用半监督学习方式和空间化距离度量标准可以增强CA算法的聚类效果,使之得到更佳的聚类性能。此外,由于本文算法保有了原CA算法的竞争学习机制,同样具备自动聚类的能力,这是如FCM和PFCM等需预先设定聚类类别数的算法所不具备的。根据人造和真实图像的实验结果,说明了本文算法确为一种有效的具备自动聚类能力且性能更佳的聚类方法,为今后在图像分割领域的应用,如医学图像分割等专业领域的分割任务提供一种新的技术手段,有着较好的应用前景。

6 结束语

针对传统CA算法存在的信息利用率低和相似度度量标准不可靠的问题,本文通过引入半监督项和样本到中心的空间距离进行改进,并加入聚类中心相似性合并的判断阈值,提出了半监督空间化CA算法。半监督项利用已知信息对隶属度矩阵进行了强化,空间化距离避免了传统欧氏距离的缺陷,加入的判断阈值进一步保证了算法整个过程中对于虚假中心的舍弃趋势。通过人造图像和真实图像2组实验,对比分析本文算法与FCM算法、PFCM算法、CA算法的性能,结果表明,本文算法能够更准确地获得聚类类别数,聚类结果更好,表现出了一定的抗噪性能。

[1] 修 宇,王士同.方向相似性聚类方法DSCM[J].计算机研究与发展,2006,43(8):1425-1431.

[2] Jain A K.Algorithms for Clustering Data[M].[S.l.]: Prentice-Hall,Inc.,1988.

[3] Frigui H.Clustering by Competitive Agglomeration[J]. Pattern Recognition,1997,30(7):1109-1119.

[4] Dunn J C.Well-separated Clusters and Optimal Fuzzy Partitions[J].Journal of Cybernetics,1974,4(1):95-104.

[5] Bezdek J C.Pattern Recognition with fuzzy Objective Function Algorithms[M].[S.l.]:Kluwer Academic Publishers,1981.

[6] Sjahputera O.Clustering of Detected Changes in Highresolution Satellite Imagery Using a Stabilized Competitive AgglomerationAlgo-rithm[J].IEEETransactions on Geoscience and Remote Sensing,2011, 49(12):4687-4703.

[7] Boujemaa N.Generalized Competitive Clustering for Image Segmentation[C]//Proceedings of the19th International Conference of the North American Fuzzy Information Processing Society.[S.l.]:IEEE Press, 2000:133-137.

[8] 刘小芳.点密度函数加权模糊C-均值算法的聚类分析[J].计算机工程与应用,2004,40(24):64-65.

[9] Tang Chenglong.New Fuzzy C-means Clustering Model Based on the Data Weighted Approach[J].Data& Knowledge Engineering,2010,69(9):881-900.

[10] Mao Qirong,Hu Suli.A Semi-supervised Recognition MethodBasedonProbabilityDistanceManifold Learning and Graph-model[J].Journal of Computer and Theoretical Nanoscience,2014,11(2):303-309.

[11] Bensaid A M,Hall L O,Bezdek J C,et al.Partially Supervised Clustering for Image Segmentation[J]. Pattern Recognition,1996,29(5):859-871.

[12] Liu Yiguang,Li Chunguang.k-NS:A Classifier by the Distance to the Nearest Sub-space[J].IEEE Transactions on Neural Networks,2011,22(8):1256-1268.

[13] Barth N.The Gramian and k-Volume in n-Space:Some Classical Results in Linear Algebra[J].Journal of Young Investigators,1999,2(1):1-4.

[14] Aster R,Borchers B,Thurber C.Tikhonov Regularization[EB/OL].(2013-01-22).http://en.wikipedia.org/ wiki/Tikhonov_regularization.

[15] Treerattanapitak K,Jaruskulchai C.Generalized Agglomerative Fuzzy Clustering[C]//Proceedings of the19th International Conference on Neural Information Processing.Berlin,Germany:Springer,2012:34-41.

[16] Deng Zhaohong.EnhancedsoftSubspaceClustering Integrating Within Cluster and between Cluster Information[J].Pattern Recognition,2010,43(3):767-781.

[17] Jing Liping,Ng M K.An Entropy Weighting k-means Algorithm for Subspace Clustering of High-dimensional Sparse Data[J].IEEE Transactions on Knowledge and Data Engineering,2007,19(8):1026-1041.

[18] Wu Kuo-Lung.Analysis of Parameter Selections for Fuzzy C-means[J].Pattern Recognition,2012,45(1): 407-415.

[19] Zhang Yunjie,Wang Weina,Zhang Xiaona,et al.A Cluster ValidityIndexforFuzzyClustering[J]. Information Sciences,2008,178(4):1205-1218.

编辑 顾逸斐

Semi-supervised Spatial Competitive Agglomeration Algorithm and Its Application in Image Segmentation

YU Ping,WANG Shitong
(School of Digital Media,Jiangnan University,Wuxi 214122,China)

Classic Competitive Agglomeration(CA)algorithm fails to take into account of the information about a few samples which are known and important during the process of cluster.Moreover,competitive agglomeration chooses Euclidean distance as a similarity metric function.But,the distance is more applicable when the distribution of the data points is spherical.This restricts the scope of its application.In order to solve these problems,the semi-supervised entry with the ability to learn is introduced to enhance membership matrix.And a distance from a sample to the spaces is used to instead of Euclidean distance,that each of them is composed of one cluster center and its nearest points.A threshold parameter about similarity of cluster centers is introduced to algorithm as the judgment for merging.The semi-supervised spatial distance competitive agglomeration is proposed.Two sets of experiments using artificial image and real images are operated,and the results show that the proposed algorithm has greater ability to get right cluster number,and gets better clustering results.

Competitive Agglomeration(CA)algorithm;similarity metric function;Euclidean distance;semisupervised;spatial distance;threshold parameter

于 平,王士同.半监督空间化竞争聚集算法及其在图像分割中的应用[J].计算机工程,2015, 41(2):234-241.

英文引用格式:Yu Ping,Wang Shitong.Semi-supervised Spatial Competitive Agglomeration Algorithm and Its Application in Image Segmentation[J].Computer Engineering,2015,41(2):234-241.

1000-3428(2015)02-0234-08

:A

:TP391.41

10.3969/j.issn.1000-3428.2015.02.045

国家自然科学基金资助项目(61170122);江苏省自然科学基金资助项目(BK2012552)。

于 平(1988-),女,硕士研究生,主研方向:多媒体技术与应用;王士同,教授。

2014-03-24

:2014-04-21E-mail:wxjn00@163.com