基于金字塔分解的自动色彩均衡算法

张 明,白松浩,邢姗姗

(中国人民解放军95899部队,北京100085)

基于金字塔分解的自动色彩均衡算法

张 明,白松浩,邢姗姗

(中国人民解放军95899部队,北京100085)

针对传统自动色彩均衡算法运算速度慢、暗区细节不明显的缺点,提出一种基于金字塔分解的自动色彩均衡算法。使用对数运算将暗区图像映射到更适合人眼观察的颜色空间,利用高斯卷积核构造图像金字塔图像序列,从金字塔最顶层图像开始进行自动色彩均衡,并对增强结果逐层进行细化,直至金字塔最底层得到最终的增强图像,细化时只需要少量像素间的比较操作,因而大幅降低了运算复杂度。实验结果表明,该算法能有效改善图像质量,保持图像细节信息,并且计算复杂度较低,便于实际应用。

图像增强;自动色彩均衡;金字塔分解;retinex理论;色彩恒常性;对数运算

1 概述

色彩恒常性是指在不同光照条件下,人眼对物体颜色有着恒定感知的能力。在图像处理领域,人们提出了一些颜色不变性模型来模拟人眼视觉特性以进行图像增强,其中以retinex和自动色彩均衡(Automatic Color Equalization,ACE)算法为主要代表。

retinex理论认为,人眼感知的颜色由物体表面的反射性质决定,而与光照信息无关。其代表算法有迭代算法[1]、中心/环绕算法[2-3]、随机路径算法[4]等。其中迭代算法计算量较大,难以自适应地确定适当的迭代次数,而迭代次数对增强结果有很大影响;中心/环绕算法运算使用高斯尺度算子估计光照图像,计算速度较快,但在图像边缘附近容易产生光晕现象;随机路径算法难以正确估计路径的起始点,容易导致图像失真。

ACE算法[5-6]也充分利用了retinex思想,强调图像的感知色彩源于与周围色彩强度的对比,并在此基础上融合了“灰界”和“白带”2个色彩均衡的模型,有很好的增强效果。但ACE算法对于图像中的所有像素都要进行两两差分运算,计算复杂度极高。本文引入多尺度分层的金字塔结构,逐层进行ACE增强计算,利用上层的增强结果对下一层进行有效预测,以提高算法的计算效率。

2 ACE算法

为叙述方便,本文所述的图像均是归一化到[0,1]的浮点数图像。

ACE算法包括2个部分:强度空间调整和动态映射。强度调整的公式如下:

式中,I(·)代表输入图像;d(x,y)表示点x,y之间的距离;sα(.)是对比度调节函数,用来增强小的图像细节,并抑制过强的边缘信息,可以采用如下公式:

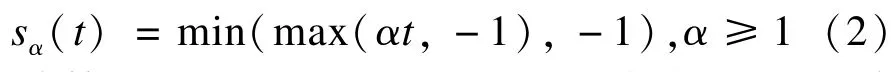
计算得到的Rc(x)已经获得了较好的增强效果,但其数据大多超出了显示范围,有必要对其进行线性映射:

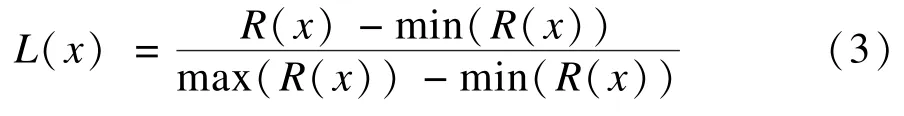
当d(x,y)≡1,α→∞时,ACE算法就相当于全局直方图均衡算法。

在现有研究文献中,ACE的改进算法主要集中对调节函数sα(.)、距离函数d(x,y)和映射方式进行调整[5-6],也有将ACE应用到HSV、对数域[7]等方面的研究,使得图像在增强细节的同时保持颜色不失真。在提高算法效率方面,可以通过选取部分像素进行差分运算[8]、变分方程[9]、模板卷积[10]、多项式逼近[11]等方式,都在一定程度上提高了算法效率。

3 改进的ACE算法

3.1 图像预处理

在对ACE算法实验中发现,如果输入图像的光照变化较大,原始ACE算法对暗区细节信息不能很好的增强显示,因此,有必要对输入图像进行非线性映射增强处理。在retinex算法中,一般都要对图像进行对数运行,从图1可以看出,log算子本质上就是对暗区像素进行了光照增强。

图1 图像对数运算

本文采取了如下的自动公式:

其中,log算子以自然数e为底,α是权重因子,α∈[0,1],取值如下:

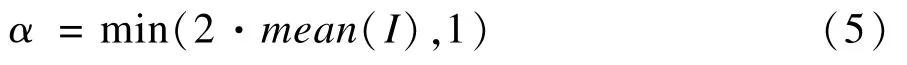
其中,mean(I)表示图像的均值,得到的I′(x)用于后续的图像增强。

3.2 金字塔运算

由于每一级金字塔图像Gk均是输入图像的不同级别的近似,那么,对每一级{Gk}进行ACE增强得到{Lk},也必然是原始图像ACE增强结果的近似。换言之,可以从金字塔的最高层开始,逐层计算ACE增强算法,在计算Lk时,可以利用Gk+1的增强结果Lk+1,即:

其中,pk为{Lk}中上下图层的细节差异,可以通过Gk和来估计。在最顶层LN,只有一个像素点,其值为0.5。在ACE算法中,每个点都与其他所有点进行比较,与距离近处点的对比关系构成细节信息,与远处点的对比关系构成背景信息,因此,只需要计算Gk和中邻域像素对pk的影响:

其中,Ω是以x为中心的邻域,M是Ω内除中心点外所有像素的个数,对比式(1)可发现,pk即是对Gk,进行邻域ACE增强的差异,除以αM是为了保证通过式(7)、式(8)得到的Lk满足0≤Lk≤1。本文算法sα(.)采用式(2),d(x,y)使用常规的欧式距离。

对L0进行线性拉伸,得到最终的增强图像。

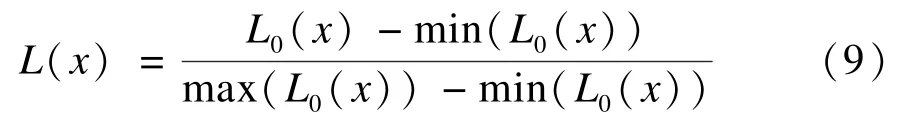
4 参数分析

在计算流程方面,本文算法和迭代retinex算法[1]有一定的共同点,都采用了图像金字塔结构,逐层进行图像预测、细化操作,直到最底层得到最终的增强图像。两者的差别主要在于,迭代retinex算法在每一层计算时都要反复与周围像素进行比较、更新操作,而本文算法采用式(8)只需要计算一次即可,计算复杂度更低。

算法中有2个主要参数:α和Ω。图2显示了不同α值对增强图像的影响,Ω取边长为7的方形区域,可以看出,随着α值的增加,图像的增强强度越大,当α过大时(见图2(f)),图像就会出现较明显的噪声,反之,当α过小时(见图2(b)),图像的部分细节信息又不够凸显,本文对多幅图像进行主观评价测试,发现取得最佳增强效果时的α大多处于区间[3,5]内,因此本文取其中间值α=4。

图3显示了Ω取不同范围时对增强图像的影响(α=4),显然,Ω值越大,算法的计算复杂度越高。Ω与图像对比度有着密切的关系。随着Ω区域的增大,输出图像的对比度逐渐增强(更有利于实验图中标牌文字的识别),当边长大于等于7时,输出图像已基本保持不变。因此,本文取边长为7,以便在不牺牲图像质量的前提下尽可能降低计算复杂度。

图2 α对算法的影响

图3 Ω对算法的影响

5 实验结果

将本文算法与传统ACE算法、文献[8]快速ACE算法和retinex增强算法进行了比较。其中retinex选择的是MSRCR算法[2],最大尺度为240,尺度数量为3,对比度增强因子1.2。

传统ACE算法和文献[8]算法采用α=4,比较结果如图4和图5所示,可以看出,4种算法都很好地增强了图像细节,但MSRCR算法的图像对比度明显偏高,图4(b)和图5(b)中都出现了较明显的噪声;文献[8]算法由于只选取部分像素进行比较运算,导致色彩保持能力偏弱,例如图4(c)和图5(c)中背景色彩偏灰;传统ACE算法的暗区部分仍然较为昏暗,例如图4(d)中左下角区域;而本文算法在细节增强和颜色保持方面都有着优异的表现。

图4 4种算法的均衡效果比较1

图5 4种算法的均衡效果比较2

在计算复杂度方面,本文算法有着更明显的优势,传统ACE算法的时间复杂度是O(N4),文献[9]将计算复杂度降低到O(N3log(N)),文献[10-11]降低到O(N2log(N)),而本文和文献[8]都将复杂度降低到了O(N2)的水平。以大小600× 400的灰度图像为例,传统ACE算法中每个像素点需要进行600×400次差分和距离运算。文献[8]每个点减少到3 200次运算(以其实验参数计算得到),而本文算法只需要(4/3)×7×7×2次运算和金字塔图像的构建操作。在统一的实验平台下(XP系统,i3 2.3 GHz处理器,2 GB内存,Matlab和c++混合编程),2张测试图像的运行时间统计如表1所示,可看出本算法在计算效率方面的提升性能。

表1 算法处理时间对比s

6 结束语

本文提出了一种基于金字塔分解的自动色彩均衡算法,该算法采用加权对数算子,能够有效增强图像细节、改善暗区图像质量,且计算复杂度较低。实验结果表明,本文算法能有效改善图像质量,色彩恢复自然,具有广阔的应用场景。但该算法离实时处理要求还有较大的差距,因此,继续降低计算复杂度和实现算法并行化是进一步研究的内容。此外,针对高动态范围图像、遥感图像、SAR图像等不同类型图像,算法的适应性研究也将是下一步的研究方向。

[1] Funt B,Ciurea F,McCann J.Retinex in Matlab[J]. Journal of Electronic Imaging,2004,13(1):48-57.

[2] Jobson D J,Rahman Z U,Woodell G A.A Multiscale Retinex for Bridging the Gap Between Color Images and theHumanObservationofScenes[J].IEEE Transactions on Image Processing,1997,6(7):965-976.

[3] Meylan L,Sosstrunk S.High Dynamic Range Image Rendering with a Retinex-based Adaptive Filter[J]. IEEE Transactions on Image Processing,2006,15(9): 2820-2830.

[4] Banic N,Loncaric S.Light Random Sprays Retinex: Exploiting the Noisy Illumination Estimation[J].IEEE Signal Processing Letters,2013,20(12):1240-1243.

[5] Rizzi A,Gatta C,Marini D.A New Algorithm for Unsupervised Global and Local Color Correction[J]. Pattern Recognition Letters,2003,24(11):1663-1677.

[6] Rizzi A,Gatta C,Marini D.From Retinex to Automatic ColorEqualization:IssuesinDevelopingaNew Algorithm for Unsupervised Color Equalization[J]. Journal of Electronic Imaging,2004,13(1):75-84.

[7] 肖志云,李新科,轩 波,等.对数域中自动色彩均衡化快速算法[J].计算机辅助设计与图形学学报, 2013,25(3):390-396.

[8] 查 炜,汪荣贵,傅剑蜂,等.基于人眼侧抑制机制的自动色彩均衡化算法[J].计算机工程,2013,39(1):7-10.

[9] Bertalm M,Caselles V,Provenzi E,et al.Perceptual Color Correction Through Variational Techniques[J]. IEEE Transactions in Image Processing,2007,16(4): 1058-1072.

[10] 袁雪庚,顾耀林.自动色彩均衡快速算法[J].计算机辅助设计与图形学学报,2005,17(10):2269-2274.

[11] Pascal G.Automatic Color Enhancement(ACE)and Its Fast Implementation[EB/OL].(2012-11-06).http:// dx.doi.org/10.5201/ipol.2012.g-ace.

编辑 金胡考

Automatic Color Equalization Algorithm Based on Pyramid Decomposition

ZHANG Ming,BAI Songhao,XING Shanshan
(95899 Unit of PLA,Beijing100085,China)

An Automatic Color Equalization(ACE)algorithm based on pyramid decomposition is proposed to solve the problems emerge after using traditional ACE,such as low speed,obscure details in dark region.The algorithm utilizes the logarithmic calculation to adjust the image obscure region and employs Gaussian kernel to build image pyramid.Color equalization algorithm is applied at the top level of the image pyramid and the result is iteratively refined layer by layer with comparison between few pixels.The simulation results show that the proposed algorithm can efficiently improve visual quality of the image,preserve the details,reduce the computational complexity and make it more suitable for practical applications.

image enhancement;Automatic Color Equalization(ACE);pyramid decomposition;retinex theory;color constancy;logarithmic operation

张 明,白松浩,邢姗姗.基于金字塔分解的自动色彩均衡算法[J].计算机工程,2015,41(2):215-218,223.

英文引用格式:Zhang Ming,Bai Songhao,Xing Shanshan.Automatic Color Equalization Algorithm Based on Pyramid Decomposition[J].Computer Engineering,2015,41(2):215-218,223.

1000-3428(2015)02-0215-04

:A

:TN919.81

10.3969/j.issn.1000-3428.2015.02.041

张 明(1981-),男,博士后,主研方向:图像处理,视频压缩;白松浩,教授、博士;邢珊珊,工程师、硕士。

2013-11-29

:2014-04-17E-mail:zmshy2128@163.com