基于1～2阶分数阶微分的图像增强算法

李军成

(湖南人文科技学院数学系,湖南娄底417000)

基于1～2阶分数阶微分的图像增强算法

李军成

(湖南人文科技学院数学系,湖南娄底417000)

在利用分数阶微分进行图像增强时,现有方法大多是基于0～1阶分数阶微分,而基于1～2阶分数阶微分的方法较少。为此,分析1～2阶分数阶微分对图像增强的作用,基于1～2阶分数阶微分构造一种用于图像增强的掩模算子。实验结果表明,该算子优于常用的频域法和空域法,比现有的一些0～1阶分数阶微分算子具有更好的图像增强效果。

图像处理;图像增强;分数阶微分;掩模算子;1～2阶微分;0～1阶微分

1 概述

图像增强是图像处理中的一个重要研究问题,也是改善图像视觉效果的一个基本手段。由于图像的边缘和纹理细节是图像信息的重要组成部分,而图像的锐化可增强图像的边缘信息和纹理细节获得更佳的视觉效果,因此图像的锐化成为目前应用最为广泛的一种图像增强方法[1]。常用的图像锐化方法按作用域可分为频域法和空域法2类,频域法是在图像的变换域中对图像的变换值进行操作后经逆变换获得增强结果,常用频域法的有理想高通滤波器、Butteworth高通滤波器等;空域法则是直接在图像平面中对图像的像素灰度值进行操作,常用的空域法有Laplacian算子等[2]。

近年来,随着分数阶微积分理论在图像处理领域中的成功应用[3-6],利用分数阶微分进行图像增强也成为一个研究热点。文献[7]构建了一种基于0～1阶分数阶微分的近似Tiansi微分算子,并将其应用于图像的增强;文献[8]提出了一种基于0～1阶分数阶微分的图像纹理增强多尺度方法;文献[9]根据近似分数阶Tiansi微分算子的作用特点,提出了3种能较大程度增强图像边缘信息的改进Tiansi微分算子;文献[10]将四元素理论与分数阶微分进行有机结合,提出了一种四元素分数阶方向微分的图像增强方法;文献[11]针对分数阶微分掩模的最佳分数阶阶数需要人为指定这一缺陷,提出了一种自适应的分数阶微分图像增强方法;文献[12]针对分数阶Tiansi微分算子的不足,提出了一种用于图像增强的改进分数阶掩模算子。由于分数阶微分不但可以较大程度地提升甚高频信号,而且还能增强中频信号,非线性保留甚低频信号,因此利用分数阶微分进行图像增强时不但能明显突出图像的边缘信息,而且还能使图像的纹理细节表现得更加清晰;文献[13-14]针对整数阶微分对图像纹理增强效果不明显的问题,分别研究了可变阶次的分数阶微分图像增强算法。

然而,现有的分数阶微分图像增强算法大多是基于0～1阶分数阶微分而建立,利用1～2阶分数阶微分进行图像增强的研究并不多见。为此,本文分析1～2阶分数阶微分对图像的增强作用,提出一种基于1～2阶分数阶微分的图像增强算法。

2 1～2阶分数阶微分

分数阶微分也称为非整数阶微分,是整数阶微分运算的一种推广。从不同的应用角度分析问题可得到不同的分数阶微分定义。经典的分数阶微分定义主要有Grümwald-Letnikov,Riemann-Liouville和Capotu定义[15]。由于Grümwald-Letniko定义是通过将经典微分定义中的阶数由整数扩展到分数推衍而来,在信号的数值实现中表现得更为精确,因此成为图像处理中较为常用的一种分数阶定义。

不失一般性,将函数s(x)的持续期[0,x]进行N等分,共得N+1个节点,这N+1个因果像素点的值分别记为:

将图像的边界作周期扩展,对图像中的非因果像素点进行处理,即:

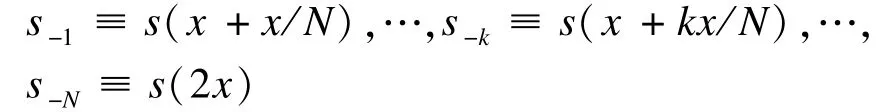
于是,基于Grümwald-Letniko定义可推导出函数s(x)的v阶微分的差分近似公式为[16]:

若补充定义Γ(1)=01=1,则式(1)中的分数阶阶次v的定义域可扩充至1≤v≤2,此时将式(1)定义的分数阶微分称为1～2阶分数阶微分。

当k=n≤N-1时,由式(1)可推导出二元函数f(x,y)在x方向和y方向上1～2阶分数阶微分的前3项近似差分表达式可表示为:

不难验证,当v=1时,式(2)与式(3)变为一阶微分的差分近似表达式,即:

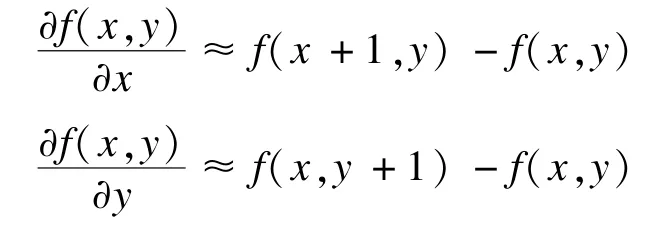
当v=2时,式(2)与式(3)变为二阶微分的差分近似表达式,即:

由此可见,1～2阶分数阶微分是一阶微分与二阶微分的一种推广。

3 微分算子对图像增强的作用分析

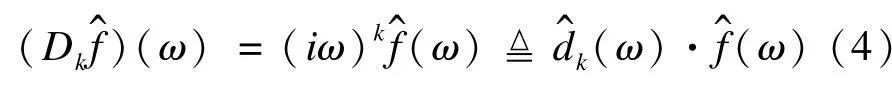
将式(4)中的整数阶微分算子Dk推广为任意阶微分算子Dv(v∈R+),则分数阶微分fv(t)在频域的形式可表示为[7]:

由式(5)与式(6)可得一阶、二阶和1～2阶分数阶微分对信号的幅频特征曲线如图1所示。

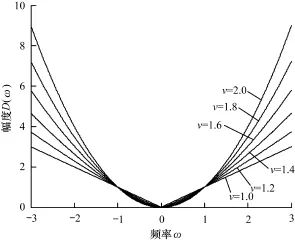
图1 微分对信号的幅频特征曲线

由图1可知,随着微分阶数的增加,微分运算对高频信号的提升作用呈非线性的增长,同时,不同阶数的微分运算对低频信号都有一定的削弱作用。一阶微分运算对甚高频信号的提升作用明显小于二阶微分运算,且对甚低频信号的削弱作用也明显大于二阶微分。虽然1～2阶分数阶微分对甚高频信号的提升作用小于二阶微分,但要大于一阶微分,高频信号得到了足够程度的提升;同时,1～2阶分数阶微分对中低频信号有一定的增强,且对甚低频信号也进行了较大程度的非线性保留。

图像的锐化是目前应用最为广泛的一种图像增强手段,它通过增强图像的边缘和纹理信息获取更佳的视觉效果。由于整数阶微分是图像锐化中最为简单通用的一种方法,而1～2阶分数阶微分作为整数阶微分的一种推广,与整数阶微分具有相似性,因此可用于图像的锐化。另外,由微分对信号的作用分析可知,利用1～2阶分数阶微分进行图像增强时,不仅可以较好地保留图像平滑区域中的低频轮廓信息,还可以非线性地增强图像中的高频边缘信息及纹理细节,其效果总体上要好于一阶微分与二阶微分。但也注意到,由于边缘和噪声都属于高频信号,当图像存在噪声时,1～2阶分数阶微分在增强边缘信息的同时对噪声也会有所增强,因此,在实际应用中,可先对图像进行去噪处理后再利用1～2阶分数阶微分进行图像增强,以获得满意的结果。

4 基于1～2阶分数阶微分模板的图像增强

4.1 模板的近似构造

由式(2)与式(3)可知,1～2阶分数阶微分前3项近似差分表达式的系数可记为:

其中,1＜v＜2。

对于二维的数字图像信号,从如图2所示的8个方向近似构造大小为3×3的1～2阶分数阶微分锐化模板。

图2 模板的8个方向

以式(7)中的ai(i=0,1,2)为元素构造近似的锐化模板。首先,由于a1为f(x,y)的系数,为了保证a1所在的坐标与模板的中心坐标(x,y)重合,以a1为中心分别将ai(i=0,1,2)按8个方向依次填充至大小为3×3的模板中,则模板的中心点系数为8a1,各领域点系数均为a0+a2;然后,将各系数除以8(a0+a1+a2)进行归一化处理,可得大小为3×3且各向同性的1～2阶分数阶微分锐化模板W,如图3所示。

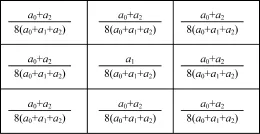
图3 1～2阶分数阶微分锐化模板

4.2 模板的特性

将模板的中心点系数与领域点系数分别记为:

其图形如图4所示。由图4可知,当1＜v＜2时,f1(v)＞0,f2(v)＜0,且f1(v)+8f2(v)≡1,这表明1～2阶分数阶微分锐化模板W与传统整数阶微分锐化模板具有类似的特点,即:(1)模板具有旋转同向性。(2)模板内系数有正数亦有负数,表示差分运算。(3)模板内所有系数之和等于1,表示对常数图像进行锐化处理时,其结果将保持不变;而对一般图像进行锐化处理时,其平均亮度将基本保持不变。

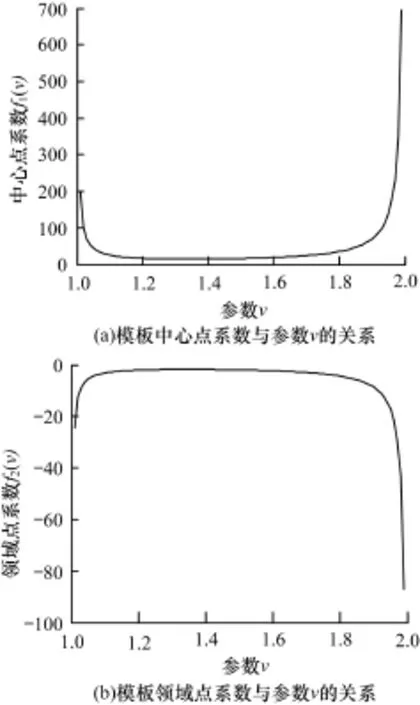
图4 模板内系数与参数v的关系

但与传统整数阶微分锐化模板不同的是,1～2阶分数阶微分锐化模板W含有1个分数阶参数v,这个参数的取值对图像边缘信息和纹理细节的增强具有重要作用。由图4可看出,当1＜v＜2时,随着v的增大,模板的中心点系数先减小后增大,而模板的领域点系数则相反,这表明随着v的增大,开始越突出领域点的重要程度,而后则越突出中心点的重要程度。因此,当分数阶参数v取不同值时,模板中心点与领域点的重要程度也不相同,于是,对于不同的图像,用户可通过调整分数阶参数v的取值获得不同的增强效果。

4.3 增强算法

设大小为M×N的自然灰度图像I(x,y),由于自然图像不可避免地会含有噪声,而1～2阶分数阶微分模板在增强边缘纹理信息的同时也会增强噪声,因此在对自然图像进行增强处理之前,可先进行去噪处理。于是,利用1～2阶分数阶微分模板进行图像增强的步骤为:

Step 1对图像I(x,y)进行去噪处理,得图像f(x,y)。

Step 2适当选取分数阶参数v(1＜v＜2),确定1～2阶分数阶微分模板W。

Step 3利用模板W对图像f(x,y)进行卷积运算,得增强后的图像g(x,y)=f(x,y)∗W。

Step 4若增强图像g(x,y)满足要求,则输出;否则,转Step2。

在利用1～2阶分数阶锐化模板对大小为M×N的灰度图像进行锐化处理时,为了保证3×3的模板能套住原图像的像素点,图像的四周不做处理,即一般是从原图像的第2行第2列的像素点开始逐点移动模板进行计算,直至第M-1行第N-1列的像素点。

显然,在利用本文算法进行图像增强时,分数阶参数v的取值决定了图像的增强效果。在实际应用中,可先对分数阶参数v赋予一个适当的数值,若所获得的增强图像不满意,则将v的取值作适当修改,直到满意为止。

所谓获得满意的增强图像,可从主观和客观2个角度进行评价,而分数阶参数v的取值应尽可能同时使主观和客观评价都满意为好。在进行主观评价时,一方面可凭人眼观察是否获得了较好的视觉效果,另一方面可利用边缘检测算子对增强图像进行边缘检测,观察图像的边缘信息和局部细节都是否有所加强;在进行客观评价时,可引入平均梯度[17]对增强图像进行定量分析。平均梯度越大,则表明图像的层次越多,也就越清晰。灰度数字图像I的平均梯度G(I)的计算公式分别为:

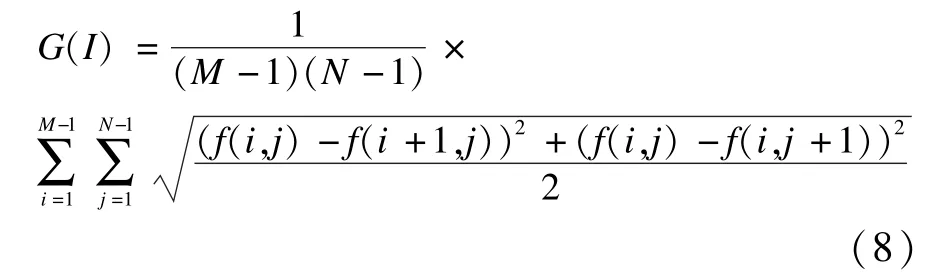
其中,f(i,j)为图像第i行第j列的灰度值;M与N分别为图像的总行数和总列数。

因此,在实际应用中,可首先依据式(8)计算出当v在区间(1,2)内取不同值(步长一般可取为0.1)时增强图像的平均梯度,找出2～3个相对较大平均梯度所对应的分数阶参数v,然后输出这些分数阶参数所对应的增强图像及其边缘检测结果,最终判断出视觉效果最佳的增强图像。

5 实验结果与分析

在PC机上(CPU:Pentium T4400,RAM:2 GB, OS:WIN7 Basic)利用Matlab7.0软件进行图像增强实验。

5.1 分数阶参数对图像增强效果的影响实验

以circuit图为例,对比观察当分数阶参数v取不同值时本文算法的图像增强效果,其中对图像所采用的去噪算法是Matlab7.0自带的3×3自适应Wiener滤波函数(下同)。依据式(8)分别计算得circuit原图的平均梯度为5.998 7,当分数阶参数v在区间(1,2)内取不同值(步长取0.1)时增强circuit图的平均梯度,如表1所示。

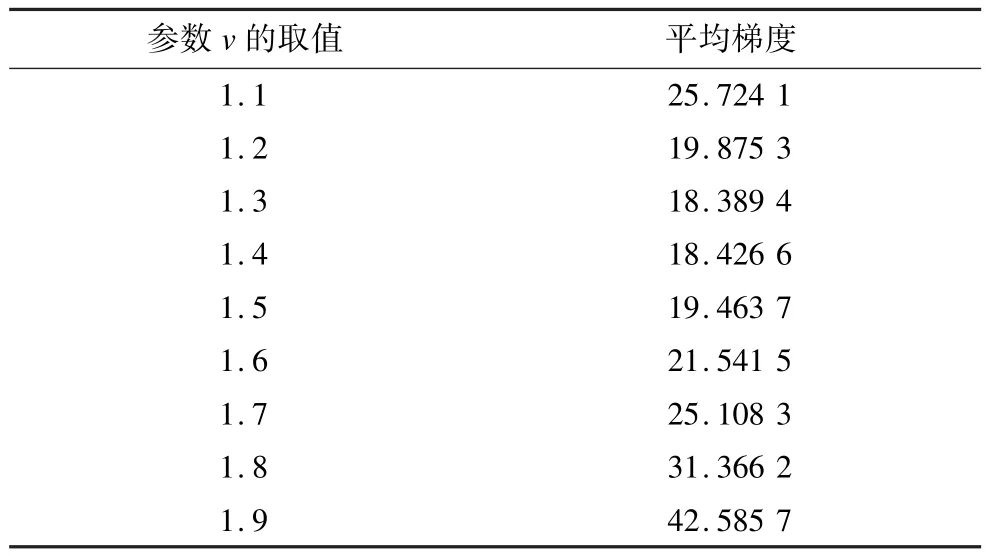
表1 参数v取不同值时增强pout图的平均梯度

由表1可知,当分数阶参数v取不同值时,增强circuit图的平均梯度都得到了较大程度的提高,且当v=1.1,1.8,1.9时增强circuit图的平均梯度相对较大,其对应的增强图像如图5所示,利用Sobel算子对图5中各图进行边缘检测的结果如图6所示。

图5 参数v取不同值时的增强circuit图

图6 增强circuit图的边缘检测结果

由图5与图6可看出,当v=1.9时所获得的增强图像出现了过亮的现象,且边缘信息和纹理细节的退化程度较为严重;当v=1.1与v=1.8时,本文算法获得的增强效果基本相当,增强图像都比原图具有更佳的视觉效果,且都能较好地增强图像的边缘信息和纹理细节,但由表1可知v=1.8时增强图像的平均梯度要大于v=1.1时的情况。综上分析,利用本文算法对circuit图进行图像增强时,最佳分数阶参数应取为v=1.8。

由于不同图像的边缘信息和纹理细节不同,最佳分数阶参数的取值也不同,因此在实际应用中,要根据不同的图像综合利用客观与主观评价方法选取最佳分数阶参数,以获得最佳的图像增强效果。

5.2 不同算法的图像增强效果对比实验

为了对比不同算法的图像增强效果,分别利用频域法中的Butteworth高通滤波器、空域法中的二阶Laplacian算子、0～1阶分数阶微分算子中的Tiansi算子[7]和改进Tiansi算子[12]以及本文算法对pout图(如图6(a)所示)进行图像增强实验。其中, Tiansi算子的最佳分数阶参数取v=0.7,改进Tiansi算子的最佳分数阶参数取v=0.5,本文算法的最佳分数阶参数取v=1.8。这里,所谓最佳分数阶参数指的是客观与主观两方面同时获得最佳增强效果是的参数。5种不同算法获得的增强pout图如图7所示,利用Sobel算子对增强pout图进行边缘检测的结果如图8所示。由图7与图8可看出,相对于其他4种算法,本文算法所获得的增强图像具有更佳的视觉效果,且能更好地增强图像的边缘信息和纹理细节。

图7 不同算法对pout图的增强效果

图8 不同算法所得增强pout图的边缘检测结果

为定量比较5种算法对pout图的增强效果,依据式(8)计算得pout原图的平均梯度为2.4821,不同算法所得增强pout图的平均梯度如表2所示。

表2 不同算法对pout图进行增强处理的平均梯度

由表2可知,本文算法所得增强图像的平均梯度明显要高于其他4种算法,这也表明本文算法可将图像的边缘信息和纹理细节表现得更加清晰。

综上所述,本文算法的图像增强效果不仅优于频域法中常用的Butteworth高通滤波器和空域法中常用的二阶Laplacian算子,而且也比现有的一些0～1阶分数阶微分算子更具优势。

在时间复杂度方面,由于本文算法先对图像进行去噪处理,然后利用3×3的掩模算子进行图像增强,其复杂度要略高于Laplacian算子、Tiansi算子[7]及改进的Tiansi算子[12],但要低于Butteworth高通滤波器,因此本文算法的时间复杂度是符合实际需要的。

6 结束语

本文主要论述了一种基于1～2阶分数阶微分的图像增强算法。当分数阶参数取定适当时,该算法获得的图像增强效果不仅优于常用的频域法和空域法,而且比现有的一些0～1阶分数阶微分算子更具优势,为图像的增强提供了一种有效的方法。由于1～2阶分数阶微分模板的分数阶参数需要人为设定,对于实时性要求较高的场合不太适用,因此如何根据图像的特点自适应选取分数阶参数值将是进一步的研究方向。

[1] Majumder A,IraniS.Perception-basedContrast Enhancement of Images[J].ACM Transactions on Applied Perception,2007,4(3):1-22.

[2] 许录平.数字图像处理[M].北京:科学出版社,2007.

[3] Liu Jun,Chen Songcan.Fractional Order Singular Value Decomposition Representation for Face Recognition[J]. Pattern Recognition,2007,41(1):168-182.

[4] Pu Yifei,Zhou Jiliu.A Novel Approach for Multi-scale TextureSegmentationBasedonFractionalDifferential[J].International Journal of Computer Mathematics,2011,88(1):58-78.

[5] Gao Chaobang,Zhou Jiliu.Edge Detection of Color Image Based on Quaternion Fractional Differential[J]. IET Image Processing,2011,5(3):261-272.

[6] Zhang Jun,Wei Zhihui.A Class of Fractional-order Multi-scaleVariationalModelsandAlternating Projection Algorithm for Image Denoising[J].Applied Mathematical Modeling,2011,35(5):2516-2528.

[7] 杨柱中,周激流.基于分数阶微分的图像增强[J].计算机辅助设计与图形学学报,2008,20(3):343-348.

[8] Pu Yifei,Zhou Jiliu,Yuan Xiao.Fractional Differential Mask:A Fractional Differential-based Approachfor Mutiscale Texture Enhancement[J].IEEE Transactions on Image Processing,2010,19(2):491-511.

[9] 王卫星,于 鑫,赖 均.一种改进的分数阶微分掩模算子[J].模式识别与人工智能,2010,23(2):171-177.

[10] 高朝邦,周激流.基于四元素分数阶方向微分的图像增强[J].自动化学报,2011,37(2):150-159.

[11] 汪成亮,兰利彬.自适应分数阶微分在图像纹理增强中的应用[J].重庆大学学报,2011,34(2):32-37.

[12] 赵 健.分数阶微分在图像纹理增强中的应用[J].液晶与显示,2012,27(1):121-124.

[13] 黄 果.可变阶次分数阶微分实现图像自适应增强[J].沈阳工业大学学报,2012,34(4):446-454.

[14] 陈庆利,黄 果,蒲亦非,等.Riemann-Liouville分数阶图像增强算法及其电路实现[J].沈阳工业大学学报, 2012,34(5):449-555.

[15] Podlubny I.Fractional Differential Equations[EB/OL]. (2010-04-13).http://dx.doi.org/10.1155/2010/215856.

[16] 张 意.分数阶微分掩模及其滤波器的构造[J].华南理工大学学报:自然科学版,2011,39(7):95-101.

[17] Groenewald A M,ArbardE,OthaEC.Related Approaches to Gradient-based Thresholding[J].Pattern Recognition Letter,1993,14(7):567-572.

编辑 顾逸斐

Image Enhancement Algorithm Based on 1～2 order Fractional Differential

LI Juncheng
(Department of Mathematics,Hunan University of Humanities,Science and Technology,Loudi 417000,China)

The present fractional differential methods for image enhancement are mostly constructed based on 0～1 order fractional differential.There are rare papers discussing the image enhancement based on1～2 order fractional differential.This paper analyses the effect of1～2 order fractional differential to image enhancement,and constructs a mask operator for image enhancement based on1～2 order fractional differential.Experimental results demonstrate that the presented operator not only has better image enhancement results than the commonly used frequency domain methods and spatial domain methods,but also has better image enhancement results than some present 0～1order fractional differential operators.

image processing;image enhancement;fractional differentiation;mask operator;1～2 order differential;0～1order differential

李军成.基于1～2阶分数阶微分的图像增强算法[J].计算机工程,2015,41(2):209-214.

英文引用格式:Li Juncheng.Image Enhancement Algorithm Based on1～2 order Fractional Differential[J].Computer Engineering,2015,41(2):209-214.

1000-3428(2015)02-0209-06

:A

:TP391

10.3969/j.issn.1000-3428.2015.02.040

湖南省自然科学基金资助项目(13JJ6081);湖南人文科技学院省级重点建设学科基金资助项目。

李军成(1982-),男,讲师、博士研究生、CCF会员,主研方向:数字图像处理,计算机辅助几何设计。

2014-03-14

:2014-05-01E-mail:lijuncheng82@126.com