改进多种群差分进化算法的混沌系统参数估计

何廷年,李晓红,蒋 芸

(1.西北师范大学计算机科学与工程学院,兰州730070;2.北京师范大学信息科学与技术学院,北京100875)

改进多种群差分进化算法的混沌系统参数估计

何廷年1,2,李晓红1,蒋 芸1

(1.西北师范大学计算机科学与工程学院,兰州730070;2.北京师范大学信息科学与技术学院,北京100875)

针对混沌系统参数估计的多峰寻优问题,提出一种改进的多种群差分进化算法。改进差分进化算法的变异操作,使其前期更适合全局性搜索,利用α核心集对当前种群进行聚类,分别对聚类后的子群选用贪婪的差分变异算子完成深度搜索,比较所选取各子群的最优值,得到全局最优值作为是否结束搜索的判断依据,并将其应用到混沌系统参数估计中。实验结果表明,该算法对于多峰值、大空间的全局性参数估计在收敛速度、精度上优于混合量子进化算法、改进粒子群优化算法以及DE/best/2算法。

α核心集;差分进化;混沌系统;参数估计;多种群

1 概述

20世纪90年代提出了混沌系统控制的概念,经过20多年的发展,混沌系统控制和同步的理论方法得到了广泛研究[1-3]。在传统混沌系统控制和同步方法中,由于混沌系统的多峰值性,在对混沌系统参数进行识别时,需要事先给定混沌系统的参数取值范围,这种对寻优参数进行限制的方法人为地降低了参数估计的难度,对于参数已知混沌系统的实验室研究是可行的,但是在实际应用中,由于混沌系统非常复杂,参数的取值范围根本无法确定,传统的参数辨识方法无法解决。针对该问题,相关学者通过构造合适的目标函数,将混沌系统参数估计问题转化为多维的系统参数优化问题,然后利用量子进化算法[4]、演化建模算法[5]、粒子群[6]、地理优化算法[7]等智能优化算法对参数进行寻优。为防止智能算法早熟收敛陷入局部极值,上述文献各自提出了改进的算法。

群智能优化算法是一种全新的演化计算方法,与人工生命特别是进化策略有着密切关系。差分进化(Differential Evolution,DE)算法作为群智能优化算法的一种,其本质是一种具有保优思想的贪婪的实数编码遗传算法。同遗传算法一样其包含交叉和变异操作,但不同于遗传算法的选择操作,差分进化算法采用一对一的优胜劣汰机制来更新种群。目前,国内学者在差分进化算法应用方面做了诸多研究。例如文献[8]应用到轧制负荷分配;文献[9]应用到机床的多道车削操作中等。

DE算法贪婪的保优特点使其具有较好的优化性能,但是种群抵抗局部极值吸引的能力大为降低,可以说基本差分进化算法更加适合于在算法后期加速收敛。对于混沌系统参数估计这种本质是多峰参数寻优的问题,当寻优空间范围过大时,差分进化算法的优化性能受其特点制约更易早熟收敛。

文献[4]引入量子算法对差分进化算法进行改进,平衡了算法全局探索与局部开发的能力,取得了很好的参数估计效果,并从量子操作的角度对差分进化算法贪婪的变异选择算子进行平衡。本文从解空间的区域划分着手,利用α核心集对种群个体进行区域划分,通过子类群体在子空间的深度搜索,避免全体种群粒子的相互干扰,使其更利于全局最优估计。

2 混沌系统参数估计

2.1 问题描述

对于如下n维混沌系统:

其中,向量θ0=(θ10,θ20,…,θd0)T为混沌系统参数的真实值;d为混沌系统参数个数;向量x0是混沌系统的初始值;向量x=(x1,x2,…,xn)T∈Rn是n维混沌系统的状态。

在对混沌系统进行参数估计时,事先假定混沌系统的结构是已知的,针对这样的系统的参数估计完全可以转化为参数寻优问题,数学描述如下:

其中,向量θ=(θ1,θ2,…,θd)T为混沌系统的参数估计值;向量y=(y1,y2,…,yn)T∈Rn为混沌待估计系统的状态。

混沌系统的参数估计问题可描述为,寻找最优的待估计参数,使得待估计系统的状态变量值与原混沌系统的状态变量值的误差最小。其中,误差目标函数可构造如下:

目标函数值越小说明待估计混沌系统与原混沌系统越接近,参数估计值越精确。

2.2 问题分析

Lorenz函数是典型的混沌系统,相关文献多以该函数进行仿真实验[4-7],为便于与相关学者研究成果进行对比,本文采用该混沌系统进行阐述。Lorenz数学描述如下:

图1 目标误差函数值随θ1,θ2的变化

文献[10]于1997年提出差分进化算法后,由于其在连续域优化问题上的性能优势,随后便引发了国内外相关学者的研究热潮。对于差分进化算法应用于混沌系统参数估计的做法是可行的,但是因为差分进化算法可以看作是贪婪的实数编码的遗传算法,所以其在保持种群多样性方面不占优势,容易陷于局部峰值。特别是在混沌系统参数估计时,相关文献一般的处理方式是对参数取值范围进行合理限制,在保证真实参数在该区域的同时,尽量回避干扰性强的峰值,在一定程度上简化了参数估计难度,对于参数范围已知的混沌系统参数估计是可行的,但是当参数的取值范围未知或者取值范围较大时,简单的差分进化算法或者通用的改进方式便不再适合。

通过分析图1可知,在不同的解空间区域内都会分布很多的局部峰值,这些局部峰值又有局部最优峰值,这些局部最优峰值便是对全局最优峰值的最大干扰,特别是当局部极值和全局极值的数量级相差不大,但是在解空间的距离较大时,该局部最优峰值对于全局最优峰值的影响是相当大的。传统的对于差分进化算法的改进方式多是平衡种群多样性和加速收敛,也就是平衡算法的勘探和开发的角度对差分进化算法进行改进,这种方式是从尽量避免陷入局部极值的角度出发来进行算法改进。但是当种群个体一旦陷于距离较远的局部最优峰值区域,传统的改进方法很难跳出。因此,本文主要是借助混沌系统参数估计来讨论针对此类多峰值问题的差分进化算法的改进方案。

3 基于α核心集的多种群差分进化算法

3.1 α核心集的有关定义

文献[11]提出一种新颖的凝聚算法,该算法设计了多层次的α核心集提取过程,随着细化过程的推进,算法的聚类中心不断增加,有利于提高算法的聚类效果,并且无需事先指定聚类中心,对非凸数据具有很好的分类效果,可以简化算法识别的难度,通过大量的仿真证明,该算法的聚类精度要好于传统的一些单层聚类算法。基于以上优点本文采用该聚类算法进行子群的识别。算法相关定义如下:

定义1高斯相似性(表示数据xi与xj的相似性):

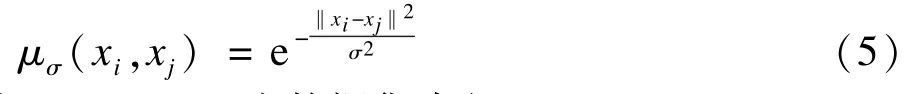
其中,σ=σ0d,d为数据集直径。

定义2首要核心集:

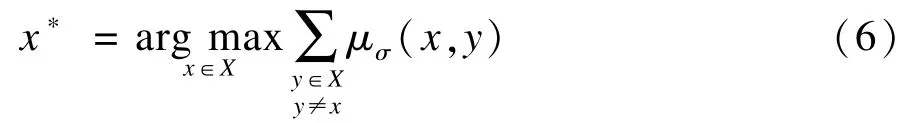
其中,x∗为任意数据集X的首要核心点。

定义3α核心集:

定义4凝聚矩阵pX～Xα:

其中,PX～Xα体现的是数据集合X与其核心集Xα的相关程度。

定义5核心集Xα数据间的相似性:

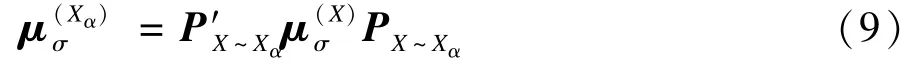
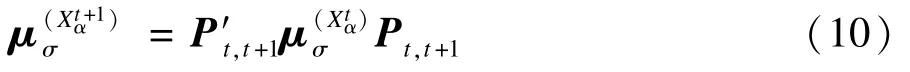
3.2 差分变异方式的改进

差分进化算法同遗传算法类似,算法的主体结构主要包括变异操作、交叉操作和选择操作。变异操作是产生新的基因的有效方式,好的变异方式可以防止进化陷于局部极值,有利于保持种群的多样性和兼顾收敛速度。因此,众多学者对差分进化算法的变异方式进行了研究,提出了多种变异方式,例如DE/rand/1式(11)和DE/best/2式(12):

不同于遗传算法及粒子群算法等生物智能优化算法,上述算法在提出变异方式时基于的理论是生物群体模拟,这里差分进化算法可以应用向量的分析方法来解释变异方式。例如式(11)变异方式中是作为向量运算的基向量,而则可以看作是扰动,这种方式变异后可以解释为在基向量附近进行扰动变异寻找比更优的个体。这种方式对于每个种群个体都是在其周围进行扰动变异,有利于保持种群多样性,但是相应的问题是如果当前种群个体没有极点附近的个体则该变异方式收敛速度将过于缓慢,对种群初始值的要求比较高。式(12)变异方式是将当前种群中适应度最好的个体作为基向量进行向量运算,这种变异方式有利于加速收敛,但是如果不是全局最优峰值而是局部最优峰值,那么这种变异方式将会加速种群个体向该局部最优进化,而无法跳出。通过分析上述2种变异方式并结合向量分析的思想,对变异方式改进如下:

全局搜索变异方式:

局部深度开发变异方式:

2种变异方式形式比较类似,主要思想是以当前种群个体i作为自身变异的基向量,这样就保证了个体i变异后的新个体位于自身附近区域,相对于式(11)、式(12)的变异方式,这种变异方式能够相对的保证新个体进化的独立性,有利于保持种群的多样性,对于防止算法早熟非常有必要。2种变异方式的不同之处是在变异扰动项中,全局搜索变异方式采用的是2个随机粒子个体,而局部深度开发变异方式采用的是当前个体i所在子群的历史最优位置和一个随机个体,这样的变化使得深度开发变异方式能够引导当前种群的个体向子群的最优个体附近进化,有助于加速收敛。

3.3 多种群差分进化算法

针对这种多峰值取值范围不确定的参数寻优问题,首先应该明确的是对于大空间进行细分采用多群体进化的方式在理论上是可行的。以前有关文献在对差分进化算法进行性能改进是多是从优化算法关键参数选取[12]、与其他优化算法混合互补[13]、优化变异方式[14]、搜索空间自适应[8]等角度进行改进,这些改进方式能够提高算法的性能,但是都不是专门针对大空间搜索的。本文在讨论混沌参数寻优时主要考虑要解决的问题有2个: (1)解决多峰值搜索问题;(2)解决参数不确定的大空间问题。文献[15]采用网格化方法是对搜索空间进行划分用来解决公交运行计划编制问题,虽然这种改进方式主要不是针对大空间搜索问题,仅仅是为了提高算法躲避不良峰值的性能,但是实际上这种改进方式对于大空间搜索问题有一定的启示作用。因此,提出一种大空间多种群智能搜索(LargeSpaceMulti-swarmIntelligenceSearch, LSMS)架构,如图2所示。图2中直观地反映出该搜索框架的关键步骤,即种群的初始化阶段、随机全局勘探阶段、子群识别阶段、多种群的深度开发阶段。这些关键步骤需要注意:(1)需要种群尽量遍布搜索空间,目前方法比较多,比如随机初始化、基于混沌映射的随机遍历等;(2)需要算法的变异方式具有足够的保持种群多样性的能力,这里需要对传统的变异方式进行改进,使其更加适合随机搜索;(3)子群识别阶段需要识别算法具有足够的精确性,并且计算复杂性越低越好;(4)深度开发阶段,这个阶段需要算法变异方式具备较强的保持种群多样性和收敛速度。

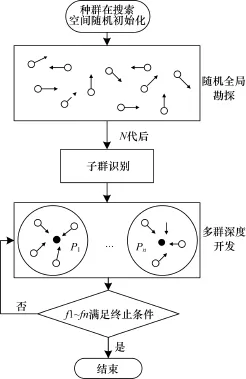
图2 大空间多种群智能搜索架构

本文对上述4个关键步骤的改进策略是:步骤(1)采用最简单的随机初始化;步骤(2)、步骤(4)根据算法需要对原有差分进化算法的变异方式进行改进(参照3.2节内容);步骤(3)采用文献[11]提出的基于α核心集的凝聚算法进行聚类识别(相关定义参照3.1节),这种聚类识别算法识别精度高,无需指定聚类中心,可以简化聚类识别难度。子群识别算法步骤为:

Step 1输入待分类的种群数据集X及所需要的子群识别个数K。

Step 3利用式(5)来计算最底层核心集的相似性矩阵,并利用式(11)计算最底层核心集的下一层核心集。

Step 4利用式(7)～式(9)计算可得:

Step 5输出各层核心集及相似性矩阵:

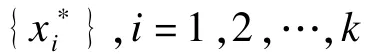
Step 7对于t=1:n依次计算:

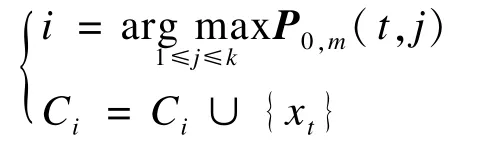
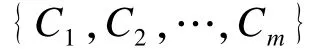
4 仿真实验与分析

4.1 Lorenz函数参数估计

本文以Lorenz函数为例对混沌参数估计问题进行阐述,首先选用Lorenz函数进行仿真,具体形式如式(4)所示。混沌参数的真实值为:θ1=10,θ2=28,。为显示大空间多种群智能搜索算法在大空间上寻优性能的优势,这里分别选取参数θ1、θ2和θ3的搜索空间{[9,11],[20,30],[2,3]},[-2 000, 2 000]以及[-2 000,2 000],对比算法采用文献[4]的混合量子进化算法(Hybrid Quantum Evolutionary Algorithm,HQEA),文献[6]的改进粒子群优化(Improved Particle Swarm Optimization,IPSO)算法以及未改进的DE/best/2算法。

算法参数设置:混沌系统采用四阶Runge-Kutta法进行常微分迭代,迭代步长设为h=0.01,种群大小n=60,维数D=3,缩放因子F=0.75,交叉概率因子CR=0.9,设置LSMS算法子群识别代数N= 45,进化代数T=500,α核心集规模控制参数m= 0.5,子群数量分别设置为:

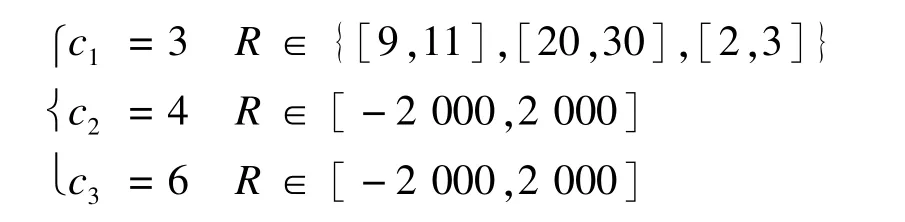
4种算法的收敛曲线如图3所示。由图3可以看出,随着搜索空间的不断增大,寻优难度逐渐增加。IPSO算法、DE/best/2算法在3种搜索空间上参数估计效果相对较差,都有早熟收敛的倾向,无法搜索到全局最优值,特别是随着搜索空间的增大,早熟现象越发明显。而HQEA算法在搜索空间{[9, 11],[20,30],[2,3]}及[-2 000,2 000]上的搜索结果尚可,但是当搜索空间扩大到[-2 000,2 000]时,HQEA算法也出现早熟收敛现象。LSMS算法在4种算法中的性能最好。

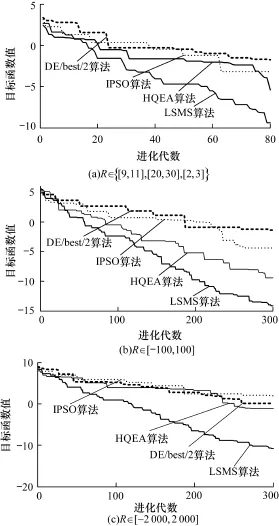
图3 目标函数收敛曲线

图4为LSMS算法参数的估计曲线(c3=6,R∈[-2 000,2 000]),可以看出,在子群识别代数t=45之后,算法能够及时跳出局部干扰峰值,快速收敛到全局最优峰值,搜索空间的扩展对于该算法的全局参数估计效果影响不大。

图4 LSMS算法的参数估计曲线

从前述分析可知,聚类识别中心数量的设置对于算法搜索性能的影响很大,子群过少影响算法的分类识别精度过低,相当于子群搜索的空间过大,对于提高全局算法收敛精度不利,子群数量过多则导致子群内的个体数量过少,影响子群内部的收敛效果,导致算法收敛速度过慢。这里以搜索空间R∈[-2 000,2 000],种群规模n=60为例进行仿真,由于子群搜索变异方式至少需要2个随机个体,因此子群的个体数量至少为3个。对c=3～10进行仿真,各运行20次求取成功率和迭代次数的平均值,为防止算法早熟无法寻找到全局最优值影响实验结果,设置最大迭代次数tmax=1000,目标函数值vtr= lg(f)=1×e-10,子群识别代数N=45。

表1数据显示出子群数量与算法性能的提高之间存在一个抛物线的关系,并非子群数量越多越好,要根据实际情况和寻优过程遇到的问题进行调整。

表1 子群数量不同时本文算法各运行20次的平均结果

4.2 Rossler函数拓展实验

前文以Lorenz函数为例阐述,4.1节以该混沌系统为例进行仿真验证,实验结果对算法的通用性说服力不强,对此,本节以Rossler函数为例进行仿真实验验证算法在混沌系统参数估计上的普适性。Rossler函数方程为:

该系统的混沌参数实际值为δ=0.2,γ=0.2,b=5.7。由4.1节仿真结果可知HQEA算法[4]的性能要优于IPSO算法以及未改进的DE/best/2算法。为了简化仿真步骤,本节对比算法只采用HQEA算法。相关算法参数设置同4.1节。各算法独立运行20次,以算法寻找到的最优、最差和平均参数估计值为评价指标。由于在搜索空间过大时HQEA算法也出现早熟收敛,为对比2种算法在合适区间的算法性能,使两者具有可比性,选取参数δ,γ和b的初始搜索空间为[-20,20],参数估计结果如表2所示。

表2 Rossler系统参数估计结果对比

表2给出的是LSMS算法和HQEA算法在Rossler系统参数估计结果,20次独立运算中,LSMS算法的最好寻优结果是找到混沌系统的参数真实值,而HQEA算法则只是找到混沌参数真实值附近的一组参数值便早熟收敛。LSMS算法最差寻优结果是找到参数真实值附近的一组参数值,而HQEA算法则完全偏离真实值,寻优效果很差,目标收敛值更为直接的说明了算法寻优效果。仿真结果显示LSMS算法同样适用于Rossler系统的参数估计,具有一定的普适性。

5 结束语

本文对混沌系统参数估计进行研究,针对参数初始搜索空间存在耦合的大空间参数估计问题,依托差分进化算法,设计一种适用于大空间多峰函数优化的LSMS算法。通过前期的随机搜索,种群个体逐步聚集到局部最优峰值附近,通过子群识别算法,将差分进化算法种群分为多个子群,子群独立进化,避免了局部最优峰值对算法收敛的干扰,从而在一定程度上起到防止早熟收敛的效果,适合对混沌系统参数的大空间全局搜索。对子群数量影响算法性能进行了实验分析,结果验证了其有效性。今后将进一步研究如何降低该算法的计算复杂度。

[1] Edward O,Grebogi C,James A Y.Controlling Chaos[J]. Physical Review Letters,1990,64(11):1196-1199.

[2] Zhao Lu,Shieh L S,Chen Guanrong.On Robust Control of Uncertain Chaotic Systems:A Sliding-mode Synthesis via ChaoticOptimization[J].Chaos,Solitons& Fractals,2003,18(4):819-827.

[3] Elabbasy E M,Agiza H N,El-dessoky M M.Global Syn-chronization Criterion and Adaptive Synchronization for New Chaotic System[J].Chaos,Solitons&Fractals, 2005,23(4):1299-1309.

[4] 张大斌,杨添柔,温 梅.基于差分进化的鱼群算法及其函数优化应用[J].计算机工程,2013,39(5):18-22.

[5] 王 柳,何文平,万仕全,等.混沌系统中参数估计的演化建模方法[J].物理学报,2014,63(1).

[6] 高 飞,童恒庆.基于改进粒子群优化算法的混沌系统参数估计方法[J].物理学报,2006,55(2):577-582.

[7] 林 剑,许 力.基于混合生物地理优化的混沌系统参数估计[J].物理学报,2013,62(3).

[8] 姚 峰,杨卫东,张 明,等.改进自适应变空间差分进化算法[J].控制理论与应用,2010,27(1):32-35.

[9] Ali R.Hybrid Taguchi-differential Evolution Algorithm for Optimization of Multi-pass Turning Operations[J]. Applied Soft Computing,2013,13(3):1433-1439.

[10] Rainer S,KennethP.DifferentialEvolution——A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J].Journal of Global Optimization,1997,11(4):341-359.

[11] 马儒宁,王秀丽,丁军娣.多层核心集凝聚算法[J].软件学报,2013,24(3):490-505.

[12] Elsayed S M,Sarke R A,Essam D L.An Improved SelfadaptiveDifferentialEvolutionAlgorithmfor Optimization Problems[J].IEEETransactionson Industrial Informatics,2013,9(1):89-99.

[13] Brest J.Differential Evolution and Differential Antstigmergy on Dynamic Optimization Problems[J]. International Journal of Systems Science,2013,44(4): 663-679.

[14] Gong Wenyin,Cai Zhihua.Differential Evolution With Ranking-based Mutation Operators[J].IEEE Transactions on Cybernetics,2013,43(6):2066-2081.

[15] 聂宗瑶,李 穗,陈吕强.基于协同差分进化的多出救点应急物资调度[J].计算机工程与应用,2013, 49(3):247-250.

编辑 刘 冰

Chaotic System Parameter Estimation of Improved Multi-swarm Differential Evolution Algorithm

HE Tingnian1,2,LI Xiaohong1,JIANG Yun1
(1.College of Computer Science and Engineering,Northwest Normal University,Lanzhou 730070,China;
2.School of Information Science and Technology,Beijing Normal University,Beijing100875,China)

In order to solve the multimodal optimization problem in chaotic systems parameter estimation,an improved multi-swarm Differential Evolution(DE)algorithm is proposed.The mutation operator of DE algorithm is improved, which is more suitable for the global search.By usingαcore set clustering the current swarm,the depth search with greed DE operator is completed on clustered swarms respectively.By comparing the optimal values of selected swarms,the global optimal value is obtained as the judgment of whether to end the search,and is applied to the parameter estimation of chaotic systems.Experimental results show that the proposed algorithm is better than the Hybrid Quantum Evolutionary Algorithm(HQEA),Improved Particle Swarm Optimization(IPSO)and original DE/best/2 algorithm in convergence rate and accuracy for multi peak,large space of global parameter estimation.

αcore set;Differential Evolution(DE);chaotic system;parameter estimation;multi-swarm

何廷年,李晓红,蒋 芸.改进多种群差分进化算法的混沌系统参数估计[J].计算机工程,2015, 41(2):178-183,188.

英文引用格式:He Tingnian,Li Xiaohong,Jiang Yun.Chaotic System Parameter Estimation of Improved Multi-swarm Differential Evolution Algorithm[J].Computer Engineering,2015,41(2):178-183,188.

1000-3428(2015)02-0178-06

:A

:TP18

10.3969/j.issn.1000-3428.2015.02.034

国家自然科学基金资助项目(61163036)。

何廷年(1979-),男,讲师、博士研究生,主研方向:人工智能,计算机视觉;李晓红,讲师、硕士;蒋 芸,教授、博士。

2014-06-20

:2014-07-28E-mail:hetingnian1979@163.com