图数据隐私保护可达性查询算法研究
2015-01-06尹树祥
尹树祥,靳 婷
(复旦大学计算机科学技术学院智能信息处理重点实验室,上海200433)
图数据隐私保护可达性查询算法研究
尹树祥,靳 婷
(复旦大学计算机科学技术学院智能信息处理重点实验室,上海200433)
数据库领域越来越多的数据通过图的结构进行存储,随着图数据规模的快速增长和云计算的兴起,数据拥有者希望将数据外包给具有强大计算能力的服务商为其客户提供查询服务。为解决数据库中的可达性查询问题,提出一种隐私保护的可达性索引和查询方法。对原始的2-hop索引构建方法进行优化,设计maxISCover启发式方法,给出根据人工节点添加算法建立pp-2-hop索引的unifyIS和unifyLS算法,并在此基础上,给出基于密文域的优化可达性查询方法。实验结果表明,基于maxISCover优化方法和unifyIS算法建立的索引大小相比于基于原始2-hop索引的方法减小1个~2个数量级。
图数据;可达性查询;2-hop索引;隐私保护;人工节点;查询服务
1 概述
随着大数据的发展,越来越多的应用通过图结构的方式存储数据,如生物信息学、社交网络以及半结构化数据XML等。尽管图数据的检索和挖掘已经有了很多经典算法,然而,随着图数据量呈现爆炸式增长,使得一个快速有效的图查询服务成为一项具有挑战性的任务。很多时候这些图数据的拥有者并没有维护这些查询服务的专业知识,因此,希望有维护查询服务专业知识和高性能集群或云计算平台的查询服务提供商(Service Provider,SP)能够为其维护这样的查询服务。但是,SP并不是一直可以值得信赖的,同时,数据拥有者不希望有未授权的用户知道他们的图数据,所以,安全和隐私保护成为服务质量[1]的一个重要衡量指标。
图数据上的可达性查询[2]是数据库领域中最为基础的查询之一。图上的可达性查询可以描述为:给定图G和2个顶点u和v,可达性查询是指通过特定的算法检验顶点u是否可以经过一定的路径到达顶点v。目前,建立高效的可达性查询索引是图数据上可达性查询的研究重点。可达性查询索引可以分为3类[3]:(1)基于传递闭包的压缩算法[4],此类算法查询效率最高效,但是其索引开销通常是最大的,有时候是不可接受的;(2)利用深度优先搜索算法或者广度优先搜索算法实现的优化在线搜索算法[5],其索引空间最小,但是通常查询时间最长;(3)基于hop的索引方法,比如2-hop[6]、TF-Label[7]、X-hop[8],和支持索引更新的hop索引方法[9]。该类算法在索引空间和查询时间方面做了一个平衡,通常具有较小的索引和较快的查询效率。
如今人们越来越重视隐私保护,然而目前没有工作能够较好地解决隐私保护的可达性查询问题。由于2-hop索引结构和查询的简单性,方便实现隐私保护,因此本文提出一种隐私保护的可达性索引和查询方法。
2 2-hop索引方法
图数据可达性查询算法通常是基于有向无环图,对于具有强连通分量的图数据,可以通过将其强连通分量转化为一个顶点,该顶点与其他顶点的可达性等同于强连通分量里所有顶点和强连通分量以外顶点之间的可达性信息。为了便于描述,在本文中,假设所有的图为有向无环图(Directed Acyclic Graph,DAG)。
对于一个图G=(V,E),图上每一个顶点u∈V都具有2个集合Lin(u)和Lout(u),这2个集合称之为顶点u的2-hop索引[6]。对于集合Lin(u)中的点,表示这些点可以到达顶点u。集合Lout(u)中的点,表示从顶点u出发可以到达的点。集合Lin(u)和Lout(u)中的点,称之为中心点。对于给定的2个查询顶点u和v,当且仅当Lout(u)∩Lin(v)≠Ø时,表示顶点u可以到达顶点v,记作u→v。
一个图G的传递闭包T是关于顶点集合V上的一个二元关系。其中,(a,b)∈T当且仅当(a,b)∈E或者有一个点v∈V,同时,(a,v),(v,b)∈T。
首先,使用一个变量T′保存T中没有被覆盖的所有元素。初始化T′=T,使用启发式算法进行迭代,使得T中的元素被覆盖并从T′中移除,当T′中的元素为空时,算法结束。
然而文献[10]发现MmaxDensCover中的分母对最后的索引大小作用很小,因此,本文提出了一个更加简单的启发式方法,称为maxSetCover,其条件如下:
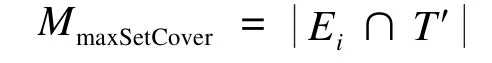
可以更加高效地建立2-hop索引。
3 隐私保护可达性查询问题定义
本节从系统模型、隐私保护目标以及攻击模型等3个方面来对本文研究问题进行定义。本文遵循数据外包领域中最常见的系统模型作为系统模型的基础,数据外包服务系统模型如图1所示。

图1 数据外包服务系统模型
该系统由3个重要组成部分:
(1)数据拥有者:数据拥有者是拥有图数据并且需要离线计算一次隐私保护的2-hop索引的一方,建立好索引后将索引数据外包给第三方服务提供商,并对授权用户进行授权。
(2)服务提供商(SP):SP通常具有强大的计算能力(例如云计算平台)和专业的服务维护知识。SP可以代替数据拥有者在密文基础上处理高并发查询请求,并将运算结果返回给用户。
(3)客户端:客户端向SP提交可达性查询请求,并从SP获得查询结果,并对结果进行解密。
在本文中,主要保护以下两方面的隐私,使得攻击者无法获取信息:
(1)查询点之间的可达性信息,这主要是希望对于一个查询,希望攻击者不能够猜测出2个顶点之间是否可达。
(2)图数据结构,使得攻击者无法从索引,以及每次的查询结果获得图数据的结构信息。
和其他所有数据外包研究中的假设一样,本文认为SP是具有好奇心的,即希望获取到包到它上面的数据信息来获得商业利益。本文假设SP可以采取以下2种攻击方式:
(1)基于密文的攻击,由于上传到SP上的所有数据都是经过加密处理的数据,因此SP只能对密文数据进行攻击。
(2)基于集合大小的攻击,假设SP尝试根据索引文件大小和查询结果集合大小来进行信息的推测。
4 图数据隐私保护的可达性查询
本节将重点介绍隐私保护的2-hop索引算法以及基于该索引的可达性查询方法。
4.1 具有Imax感知的2-hop索引算法

实验发现通过maxDensCover和maxSetCover启发式方法构建的2-hop索引Imax通常较大。较大的Imax通常会导致需要加入更多的人工节点来达到隐私保护的目的。
在本节中,提出了一种新的启发式条件使得建立2-hop索引的过程中能够使得Imax尽可能最小。其主要思想是在建立2-hop索引的过程中将交集的信息考虑进去。该启发式条件的任务主要是最小化以下的2个指标:
(1)2-hop索引的大小;

为了达到以上的2个目标,本文提出了一种新的启发式方法,称之为maxISCover:

其中,u∈Lw,v∈Rw。该方法包括以下2个部分信息:
(1)|Ew∩T′|表示如果在该次迭代中选择w为中心点的话,那么通过选择该中心点能够覆盖T(G)中未覆盖的元素的数目。
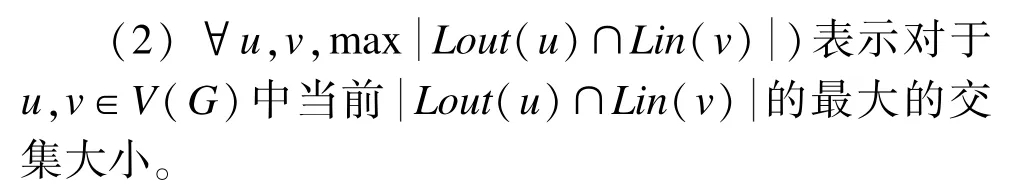
通过将以上2个部分信息结合起来,表示在每一次选择中心点时,希望该中心点既可以尽可能多的覆盖未被覆盖的传递闭包元素,同时使得所有的Louts和Lins之间的交集尽可能小。
4.2 人工节点添加算法
在本节中,通过使用2个人工节点添加算法来对4.1节中建立的2-hop索引进行处理,使得其可以满足第3节中定义的隐私保护目标。同时,为了满足隐私保护的目的,期望向原始的2-hop索引中引入一些人工节点使得所有的Louts和Lins之间的交集大小一致。最后,通过再引入一些人工结点使得所有的Lout(Lin)集合里面的元素数目都能在一个用户指定差值阈值之内,以防止SP可以通过基于集合大小的攻击方法来对索引信息进行推测。
4.2.1 交集大小的归一化
交集大小归一化主要处理的问题是如何通过向2-hop索引(Lins和Louts)中引入一些人工节点来实现对于所有的u,v∈V,Lout(u)和Lin(v)的交集大小为一个定值Imax。本文将这个问题称之为最少人工节点添加问题。下面给出最少人工节点添加问题的定义。
定义2最少人工节点添加问题是对于给定一个图G的2-hop索引,通过向Lins和Louts中添加一些人工节点得到使得:

很容易证明最少人工节点添加问题是一个NP-hard问题。具体的证明见文献[11]。针对该问题,本文中提出了一种贪心算法,称之为unifyIS算法,具体的算法见算法1。
算法1交集大小归一化算法(unifyIS)
输入2-hop索引(Lins和Louts)
输出添加了人工节点后的2-hop索引

算法1中F(i,k)表示如果将节点k添加到当前的Lin(i)中,可以使得当前的Lin(i)和多少的Lout(v),v∈V的交集大小增加1。如果是重复利用一个已有的节点,则可以通过向Lin(i)中添加一个节点带来F(i,k)对的交集大小增加1,此时F(i,k)≥1。如果所有的已有的节点都不能重复利用,则同时向当前的Lin(i)和m个对应的Lout(v),v∈V中添加一个新元素,使得添加m+1个节点,带来m对交集大小的增加,此时F(i,k)<1。算法1总是先寻找F(i,k)≥1的元素进行添加,在没有这样的元素之后,通过引入一个新的元素,并更新大顶堆H中所有的元素。进行下一步的迭代。当所有的交集大小都为Imax时,算法终止。
4.2.2 索引大小的归一化
在4.2.1节中,最少人工节点添加问题已经是NP-hard问题了,所以,在算法1中只考虑了如何使得任意2个集合之间的交集大小一致,但是通常由unifyIS算法建立出的2-hop索引中的Lins和Louts集合元素个数差距较大。为了防止攻击者利用索引集合大小的信息对图中一些具有较高或者较低的出度或入度的顶点信息进行推测。在本节中提出一种后处理的Lins和Louts集合大小归一化处理算法unifyLS。由于对Louts的归一化和Lins是完全一样的过程,因此为了描述的简洁性,这里只讨论如何归一化Lins的大小,对于Louts可以使用和Lins完全一样的算法进行处理。
本文使用Linmax和Loutmax分别表示Lins和Louts中最大的集合大小。算法主要思想基于以下想法:
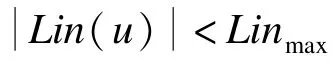
(2)算法保证在对任何中心点进行分裂的过程中,不增加Imax大小。
下面给出索引大小归一化问题的严格定义。
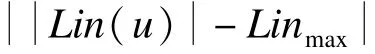
本文在算法2中介绍了ULS算法来解决索引归一化问题。
算法2索引大小归一化算法(unifyLS)
输入交集大小归一化后的2-hop索引
输出索引大小归一化后的2-hop索引

在算法2中,第1行对于每一个顶点u的Lin(u),如果发现它的集合大小小于Linmax。在算法第2行和第3行,从当前的Lin(u)中选择一个人工节点,并将其分裂为n+1个新的人工节点。在第4行中,使用分裂后的节点集合代替原来的节点w。在算法第5行~第10行,针对其他顶点的Lin(v)和Lout(v),v∈V的不同的大小和是否包含节点w的情况,分别根绝算法进行相应的处理,以使得在替换节点的同时保证所有集合之间的交集大小保持Imax不改变。
通过以上的索引大小归一化算法处理后的2-hop索引的任意集合之间的交集大小并未改变,与此同时,算法总是使得距离目标远的集合的增长速度大于距离目标近的集合,最后可以交替在Lins和Louts上使用索引大小归一化算法直到每一类集合之间的大小满足定义的阈值δ。
4.3 索引加密处理算法
在4.2节中,通过引入unifyIS和unifyLS算法使得任何2个Lins和Louts集合之间的交集大小都等于Imax同时使得所有的Lins和Louts的集合大小都在一个规定的阈值范围内。在本节中,介绍如何对索引进行加密以满足安全性要求。
为了区分在索引中,哪些是原始2-hop索引中真实的中心点,哪些是通过算法引入的人工中心点,本文对2-hop索引中的中心点使用一个标志位来表示它的真实与否,具体见定义4。
定义42-hop索引中的每一个中心点都是一个二元组(w,f),当该w中心点是一个真实的中心点时f=0,否则f=1。
基于定义4,文中对所有的中心点进行加密使得既可以保护查询点之间的可达性信息也可以保护图的结构信息。为了隐藏图中顶点和索引中中心点的联系,对(w,f)中的w和Lin(u),Lout(u)中的u使用带有不同参数的单向哈希函数来对这2类点进行映射,把这2个带有不同参数的哈希函数分别标记为hs1(w)和hs2(u)。使用不同的参数使得对于w=u,hs1(w)≠hs2(u)。关于二元组中标志位的加密,文中使用乘法同态加密算法Elgamal算法(E(f))对其进行加密。采用Elgamal加密算法主要有以下好处:(1)由于标志位只有2种不同的值0或1, Elgamal算法在加密时引入随机数使得相同的值可以被加密成不同的密文,因此使用Elgamal算法可以使得加密后的密文域变大,进而SP无法通过对相同的标志位进行统计以获得标志位信息。(2)由于Elgamal算法是乘法同态加密算法,可以减少客户端的解密计算量。
至此已经完成了隐私保护的2-hop索引的创建,下面给出隐私保护的2-hop(pp-2-hop)索引的精确定义。
定义5对于一个图G=(V,E),它的pp-2-hop索引就是对于图中每个加密的顶点ue(ue=hs2(u))都带有2个加密的集合Lout(ue)和Lin(ue)表示顶点u的可达性信息。其中,对于集合Lout(ue)和集合Lin(ue)中的每一个元素都是一个二元组(we,fe),we=hs1(w),fe=E(f)。
4.4 隐私保护的可达性查询处理
基于4.3节中建立的pp-2-hop索引,本节介绍如何在SP不需要对索引进行解密的情况下进行可达性查询。查询处理主要有以下3个步骤:(1)客户端对查询内容(u,v)进行加密,使用hs2(·)哈希方法进行映射处理,将查询内容映射成(ue,ve),并将其提交到服务商SP进行查询;(2)在服务端SP对集合Lout(ue)和Lin(ve)进行集合交集操作,将交集后的结果Re返回给客户端;(3)客户端使用从数据拥有者处通过授权获得的密钥K通过Elgamal解密程序对Re进行解密并得到结果。
在朴素的查询算法中,在上述的查询步骤的步骤(3)中,服务商将所有的交集结果中的标志位返回给客户端。由于在索引算法中,保证了所有的查询结果的大小都为Imax,因此客户端需要对所有的Imax个加密后的标志位信息进行解密,直到找到一个解密后为0的结果,说明查询点u可以到达顶点v。很明显,在这种算法中,客户端解密次数最多要解密Imax次,由于解密是一件很耗时的事情,因此本文提出一种基于乘法同态加密算法的查询处理方法。
在基于乘法同态加密算法的查询算法中,客户端只需要进行一次解密操作就可以得到最终的查询结果。将2个查询点(ue,ve)的Lout(ue)和Lin(ve)的交集结果记为:
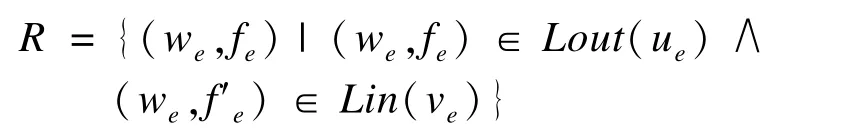
由于标志位是使用的乘法同态加密算法Elgamal进行实现,所谓乘法同态是指密文下的乘法运算结果等于明文下的乘法再进行加密,因此密文下的乘法运算结果进行解密就等于明文下的乘法结果。所以,最终的查询结果可以定义为:
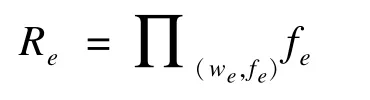
最终将Re返回给客户端,客户端私用私有密钥进行一次解密,如果得到结果为0,表面顶点u可以到达顶点v,否则不可达。
5 隐私分析
本节针对之前定义的攻击模型和保护目标,对本文提出的可达性索引和查询方法安全性进行分析。
首先,分析攻击者在查询算法进行的每一步攻击者SP可以获取到的信息。对于一个给定的查询(ue,ve),SP首先会在pp-2-hop索引中检索到Lout(ue)和Lin(ve),然后SP求得这2个集合的交集,并在基于Elgamal加密后的标志位上进行乘法运算进而得到最终的返回结果Re。
由于SHA-1哈希算法和Elgamal算法在安全领域都被证明是没法攻破的,因此SP无法破解哈希算法,它就无法破解出查询点ue,ve的真实信息,同时,它也无法破解出索引中的中心点信息,那么它就无法在这2类点之间找到映射关系,进而无法猜测出哪些中心点是人工节点。同时,由于SP无法破解Elgamal算法,因此它不能破解索引中的标志位信息,进而同样无法判定一个点是否为真实中心点或者人工节点。基于以上2点,由于SP无法辨别中心点的真实性,它无法获知一个查询的结果信息,因此它无法破解查询点之间的可达性信息。由于所有的查询都无法获取可达性信息,因此它无法破解图的结构信息,它始终不知道图中任意2个点之间的可达性。
其次,由于通过算法使得所有的交集集合大小均为Imax,因此对于任何的查询,从SP使得角度,它获得的信息是一致的。所以,它无法从查询结果的大小来推断查询点之间的信息。由于所有的索引集合大小都完全相同,因此SP也无法从索引集合的大小推测出图中某些点的度的信息。
综上,证明隐私保护的2-hop索引和查询算法可有效保护查询点之间的可达性信息和图结构信息。
6 实验结果与分析
本节通过实验验证本文算法的效率以及对原始2-hop算法的优化效果。实验环境为Intel i3-2310 2.10 GHz CPU,4 GB内存,Windows7操作系统,文中的算法用C++实现。实验中的哈希函数采用160 bit SHA-1算法,加密算法是1024 bit Elgamal算法。
实验使用4个真实数据集[12]来进行实验效果的验证,关于这些数据集信息见表1,其中,G表示数据集名称;|V|表示图的顶点个数;|E|表示图的边数;|E|/|V|表示图的稀疏性。对于每个数据集生成1000个随机的查询,50%为可达的查询;另外50%为不可达的查询。
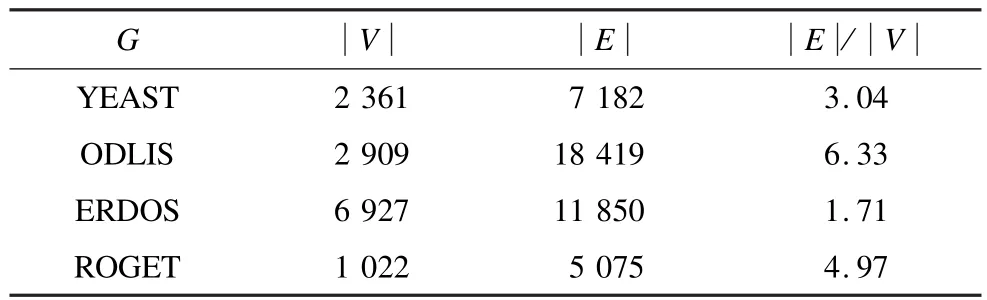
表1 数据集信息
在表2中,比较了3种不同的启发式方法条件下,建立出的2-hop索引中的最大的交集集合大小Imax的比较。从表中很明显看出通过maxISCover启发式方法条件创建出的索引的最大交集集合大小Imax要比其他2种启发式条件要小很多。其主要原因在于利用maxISCover启发式方法条件建立2-hop索引时,在每一次迭代中,总是将当前的Imax考虑到索引的建立过程中,所以每次总是选择能够覆盖尽可能多的传递闭包集合元素同时使得Imax尽可能小的中心点。从具体数据来看,maxIScover方法比maxDens-Cover方法和maxSetCover方法的实验结果要好108倍和1.43倍。
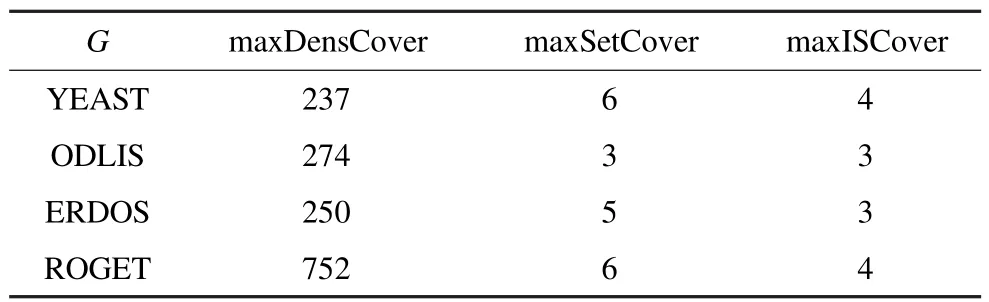
表2 不同启发式条件下最大交集大小Imax比较
观察交集大小归一化算法在不同的Imax条件下的效果。在表3比较了交集大小归一化后的索引大小。

表3 不同启发式条件下unifyIS算法效果比较
从表中可以看出,在基于maxISCover启发式方法条件下,由于Imax是最小的,然后对比表中不同的启发式条件下添加人工节点后的索引大小,可以看出unifyIS算法可以保证在添加人工节点后的索引大小要比最坏的|V2|级别要小1个~2个数量级。本文中的算法在所有的数据集上都具有较好的结果。
在表4中,列出了对于一个可达性查询在SP端和客户端所需要的时间,表中的时间是1000个查询平均后每个查询的时间。
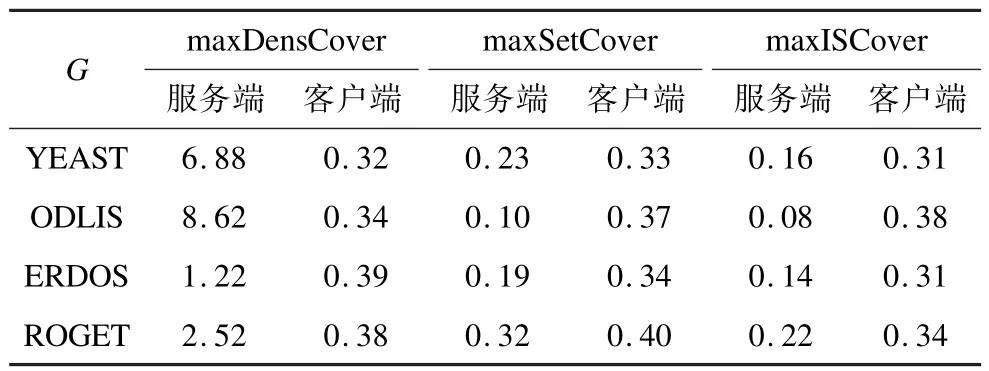
表4 服务端和客户端的查询时间ms
从表4可以看出,几乎所有的服务端的查询时间与Imax成正相关,其主要原因在于服务端SP的查询时间在于集合求交集和对Imax个标志位进行密文域上的乘法操作这两部分构成,集合的交集可以在几乎可以忽略不计的时间内完成,SP端的时间差距在Imax个密文域的标志位乘法运算。本文提出的maxISCover方法具有较小的Imax,因此,SP端本文的算法查询效率较高。所有的算法客户端都只需要进行一次解密操作,所以,所有的客户端的查询时间都几乎一致,并且客户端查询时间较快,用户可以接受。
7 结束语
本文对图数据隐私保护可达性查询问题进行研究。首先对原始2-hop索引建立算法的启发式方法进行优化,并针对优化后的2-hop索引引入了unifyIS算法和unifyLS算法,以构建隐私保护的2-hop索引(pp-2-hop)。基于pp-2-hop索引,提出隐私保护的查询方法及其优化方法。同时,对提出的pp-2-hop索引和查询方法的安全性进行分析和证明,结果表明了该算法的有效性。今后将考虑如何基于pp-2-hop索引结构实现隐私保护的最短路径查询。
[1] Menezes D A.QoS Issues in Web Services[J].Internet Computing,2002,6(6):72-75.
[2] 李先通.图数据查询技术的研究[D].哈尔滨:哈尔滨工业大学,2009.
[3] Jin Ruoming.Scarab:Scaling Reachability Computation on Large Graphs[C]//Proceedings of SIGMOD’12. Scottsdale,USA:ACM Press,2012:169-180.
[4] Schaik S J,Moor O.A Memory Efficient Reachability Data Structure Through Bit Vector Compression[C]// Proceedings of SIGMOD’11.Athens,Greece:ACM Press,2011:913-924.
[5] Seufert S.Ferrari:Flexible and Efficient Reachability Range Assignment for Graph Indexing[C]//Proceedings of ICDE’13.Brisbane,Australia:IEEE Press, 2013:1009-1020.
[6] Cohen E.Reachability and Distance Queries via 2-hop Labels[J].SIAM Journal on Computing,2003,32(5): 1338-1355.
[7] James C,Huang Silu.Tf-label:A Topological-folding Labeling Scheme for Reachability Querying in a Large Graph[C]//Proceedings of SIGMOD’13.New York, USA:ACM Press,2013:193-204.
[8] 舒 虎,崇志宏,倪巍伟,等.X-Hop:传递闭包的多跳数压缩存储和快速可达性查询[J].计算机科学, 2012,39(3):144-148.
[9] 刘旭辉,冯建华,洪 亲.一种支持更新的图可达性查询算法[J].计算机科学,2007,34(10):49-52.
[10] Cheng Jiefeng,Jeffrey X Y.Fast Computation of Reachability Labeling for Large Graphs[C]//Proceedings of EDBT’06.Munich,Germany:ACMPress,2006: 961-979.
[11] Yin Shuxiang,Jin Ting.Privacy Preserving Reachability Query Algorithm[EB/OL].(2012-10-21).http:// admis.fudan.edu.cn/member/sxyin/proof.pdf.
[12] Vladimir B.Pajek Datasets[EB/OL].(2013-01-21). http://vlado.fmf.uni-lj.si/pub/networks/data/.
编辑 刘 冰
Research on Privacy Protection Reachability Query Algorithm of Graph Data
YIN Shuxiang,JIN Ting
(Key Lab of Intelligent Information Processing,School of Computer Science,Fudan University,Shanghai 200433,China)
Due to the massive volume of graph data from a wide range of recent applications and unprecedented graph data growth,it is becoming economically appealing for data owners to outsource their data to a powerful Service Provider (SP),such as a cloud computing platform,which provides high computational query services.This paper studies a novel privacy preserving 2-hop index and query algorithm for a fundamental query for graphs namely the reachability query.It optimizes the existing method for building 2-hop index,proposes one optimizing method(maxISCover),and two algorithms(unifyIS and unifyLS)to build privacy preserving 2-hop(pp-2-hop)index by adding some surrogate nodes, and raises up an optimized query processing algorithm based on pp-2-hop index.Experimental results show that the index size of this algorithm based on maxISCover optimization method and the unifyIS is reduced by1~2 orders of magnitude, compared with the method based on the original 2-hop.
graph data;reachability query;2-hop index;privacy protection;artificial node;query service
尹树祥,靳 婷.图数据隐私保护可达性查询算法研究[J].计算机工程,2015,41(2):167-172.
英文引用格式:Yin Shuxiang,Jin Ting.Research on Privacy Protection Reachability Query Algorithm of Graph Data[J].Computer Engineering,41(2):167-172.
1000-3428(2015)02-0167-06
:A
:TP391
10.3969/j.issn.1000-3428.2015.02.032
尹树祥(1989-),男,硕士研究生,主研方向:机器学习,模式识别;靳 婷,博士研究生。
2014-04-08
:2014-04-29E-mail:sxyin@fudan.edu.cn
