基于二次剩余的匿名代理者签密方案
2015-01-06杨启良
刘 祯,杨启良,杨 波
(1.陕西师范大学计算机科学学院,西安710062;2.树德科技大学信息学院,中国台湾高雄82445)
基于二次剩余的匿名代理者签密方案
刘 祯1,杨启良2,杨 波1
(1.陕西师范大学计算机科学学院,西安710062;2.树德科技大学信息学院,中国台湾高雄82445)
由于现有签密方案大多基于双线性对,配对运算计算量较大,且实现效率不高,不能满足对代理签密者的匿名要求,因此无需配对的签密方案是密码学的研究方向。而基于二次剩余的签名方案不仅具有描述简单,能够抵抗选择密文攻击的优点,且相较于基于配对的签名方案具有更高的实现效率。为此,将二次剩余的方法应用到签密方案中,并结合匿名性,提出一种基于二次剩余的匿名代理者签密方案。分析结果表明,该方案具有匿名性与公开验证性。
代理者签密;匿名性;二次剩余;随机预言机模型;公开验证;可追踪性;不可否认性
1 概述
1997年,文献[1]提出了签密体制,即在一个合理的逻辑步骤内同时完成数字签名和公钥加密2项功能,而计算量和通信成本都低于传统的“先签名后加密”。在文献[1]提出签密体制后,签密就得到了广泛的应用,如电子支付、移动代理安全等。随着签密体制的广泛应用以及应用场合的不同,又有许多新的有效的签密体制被相继提出[2-4]。1999年,文献[5]首先提出了代理签密体制。代理签密体制主要是为了满足原始签密者由于出差等原因无法亲自对消息进行签密,而将签密权利授权给代理签密者。授权信息一般包括原始签密者的身份信息、代理签密者的权利范围和代理签密的时间限制等。随着代理签密体制的广泛应用,又衍生出来新的代理签密体制,如基于身份的代理签密体制[6]、无证书的代理重签密[7]等。
现有的大多数代理签密方案都是基于双线性对的,而配对运算需要很大的计算量,故使用无配对的签密方案是密码学的研究方向。近年来,由于基于二次剩余构造的签名方案几乎对明文空间没有限制,描述简单,并且可抵抗选择密文攻击,因此使用二次剩余构造的签名方案得到了广泛研究。2000年,文献[8]利用二次剩余提出了一个新的Rabin签名方案,又在2005年文献[9]利用二次剩余提出一个基于身份的签名方案。2001年,文献[10]利用二次剩余构造了一个基于身份的签名方案。2009年,文献[11]也提出了一个利用二次剩余构造的基于身份的签名方案。2012年,文献[12]不仅利用二次剩余构造出了一个代理签名方案,同时比较了基于二次剩余困难问题的代理签名方案与基于其他数学难题的代理签名方案,得出基于二次剩余困难问题的方案在抵抗相同敌手的情况下具有更高效率的结论。由此,可以看出基于二次剩余构造方案具有很重要的研究意义。
2005年,文献[13]提出一种新型代理签名方案,该方案指出在很多特殊的场合下,原始签名者并不希望验证者知道代理签名者的身份,从而将代理签名者的身份保护起来,使得验证者从签名结果中无法获取代理签名者的身份信息。本文通过将代理签密与身份隐藏相结合,构造一种基于二次剩余的匿名代理者签密方案,并给出预言机模型下的安全性证明。
2 预备知识
2.1 二次剩余
定义1 设n是正整数,a是整数,(a,n)=1。若同余式x2≡amodn有解,则a为模n的平方剩余(或二次剩余);否则,a为模n的平方非剩余(或二次非剩余)。定义符号Qn为二次剩余,为二次非剩余。
2.2 勒让德符号
定义2 设p是素数,a是整数,定义勒让德符号如下:

2.3 合数的二次剩余
命题1设N=pq,其中,p和q是不同的素数;且满足y=yp·yq。当yp为关于p的二次剩余,yq为关于q的二次剩余,则y是一个关于模N的二次剩余[14]。


2.4 Blum整数
定义3若p,q为不相等的素数,且p,q均为模4与模3同余的素数,则称N=pq为Blum整数。
2.5 Williams整数
定义4设N为一个合数,N=pq,且p,q是不同的素数,其中,p=3mod8,q=7mod8,则称N为Williams整数。

定理2若x∈Jn,N=pq是一个Blum整数,则有:


3 匿名代理者签密方案模型
3.1 匿名代理者签密系统的定义
方案中有3个参与者:原始签密者Alice、代理签密者Bob和验证者Verifier。7个算法,即初始化、公私钥对生成算法、身份存储算法、委托算法、代理签密算法、解签密算法、揭示代理签密者身份算法。具体如下:
(1)初始化:输入参数1n,输出系统所用的参数params。
(2)公私钥对生成算法:输入系统参数params,输出Alice、Bob和Verifier的公私钥对(PKa,SKa), (PKb,SKb)和(PKv,SKv)。
(3)身份存储算法:输入系统参数params、Bob的身份信息ID、Bob生成的随机值R,输出Bob的身份信息的数字签名σ1。Alice存储此签名。
(4)委托算法:输入系统参数params、授权信息mw和Alice的私钥SKa,输出Alice委托Bob的委托签名σ2。
(5)代理签密算法:输入系统参数params、委托信息mw、Alice的公钥PKa、Alice生成的随机值Ra、Bob的私钥SKb,生成代理签密私钥(PK0,SK0)。输入Verifier的公钥PKv和签密的消息m,输出签密消息σ。
(6)解签密算法:输入系统参数params、签密结果σ和Verifier的私钥SKv,验证消息的有效性并恢复消息m。
(7)揭示代理签密者身份算法:输入签密结果σ和Alice的公钥PKa,Alice验证签密消息是否有效。若有效,输出代理签密者的身份信息ID。
3.2 匿名代理者签密系统的安全性
方案的安全性需求包括机密性、强不可伪造性、强不可否认性、匿名性、公开验证性、可追踪性和防止代理权滥用。具体如下:
(1)机密性:从签署的密文中,只有验证者才可以恢复出明文消息,其他任何人通过密文获得消息的任何内容在计算上都是不可行的。
(2)强不可伪造性:任何第三方,包括原始签名者,如果未被指定作为代理签名者,都无法产生有效的代理签名。
(3)强不可否认性:在签密出现争议的时候,原始签密者可以揭示代理签密者的身份,并且对这个身份信息,代理签密者无法否认。
(4)匿名性:验证者无法从签密结果,授权信息等获得代理签密者的身份信息,只有通过原始签密者才可以揭示代理者的身份。
(5)公开验证性:任何人可以验证签密结果的有效性,判断此签密是否为一个原始签密者承认的有效签密。
(6)可追踪性:原始签密者可以追踪代理签密者的身份信息。
(7)防止代理权滥用:代理签密者签署消息不能超出委托信息的范围,如果滥用,则造成的后果将由代理签密者负责,并且代理权是不可转移的。
3.3 不可伪造性的攻击模型
为了定义合理的攻击模型,假设敌手拥有更大的自由度,可以模拟现实生活中的各种行为。攻击模型中除了一个外部攻击者,还有2种类型的内部攻击者。
类型1A1是一个外部敌手,只有Alice和Bob的公钥。
类型2A2是一个恶意签密者,有Bob的私钥。
类型3A3是一个恶意原始签密者,有Alice的私钥。
显然,如果这个签密系统可以抵抗第2类型和第3类型的恶意敌手,那么它一定可以抵抗第1类型的敌手。为此,构造2种类型的攻击模型。
下面证明匿名代理签密方案在第2类型的敌手A2攻击下存在不可伪造性。
代理签密系统在第2类型的敌手A2攻击下存在不可伪造性,即没有给定委托证书mw,或者即使获得符合委托证书mw的消息m,伪造一个有效签密也是困难的。为了描述匿名代理签密方案在第2类敌手攻击下具有不可伪造性,构造一个参与者为挑战者C和第2类型的敌手A2的交互游戏:
(1)初始化:挑战者C运行初始化算法得到系统参数,运行公私钥对生成算法,得到原始签密者Alice和代理签密者Bob的公私钥对(PKa,SKa)和(PKb,SKb),之后挑战者C发送(PKa,PKb,SKb)给敌手A2。
(2)敌手A2进行一系列(多项式有界次)适应性询问。
(3)委托询问:A2询问委托信息mw。挑战者C运行委托算法得到σw,并将σw发送给A2。
(4)代理签密询问:A2询问关于σw的消息m的代理签密。挑战者C运行代理签密算法,得到签密σ,并将σ返回给A2。

定义5如果没有任何多项式有界的第2类敌手A2在多项式时间t内,以qw次委托询问,qps次代理签密询问,以一个比ε更大的优势赢得上面的游戏,则称匿名代理签密方案在适应性选择消息攻击下是(t,qw,qps,ε)存在性不可伪造的。
下面证明匿名代理签密方案在第3类型的敌手A3攻击下存在不可伪造性。
代理签密系统在第3类型的敌手A3攻击下存在不可伪造性,也就是说原始签密者很难对消息m∗生成一个指定为代理签密者的有效签密。为了描述匿名代理签密方案在第3类型的敌手攻击下存在不可伪造性,构造一个参与者为挑战者C和第3类型的敌手A3的交互游戏:
(1)初始化:挑战者C运行初始化算法得到系统参数,运行公私钥对生成算法,得到原始签密者Alice和代理签密者Bob的公私钥对(PKa,SKa)和(PKb,SKb)。之后,运行代理签密算法,得到代理签密公私钥对(PK0,SK0)。挑战者C发送(PK0,PKa,SKa)给敌手A3。
(2)代理签密询问:敌手A3运行关于σw的消息m的代理签密询问。挑战者C运行代理签密算法,得到签密σ,并将σ返回给A3。

定义6如果没有任何多项式有界的第3类敌手A3在多项式时间t内,以qps次代理签密询问,以一个比ε更大的优势赢得上面的游戏,则称匿名代理签密方案在适应性选择消息攻击下是(t,qps,ε)存在性不可伪造的。
4 方案实现
本文方案利用二次剩余进行设计。可以用签密者的门牌号或者电子邮箱等作为代理签密者的身份信息ID。其中,(Na,pa,qa)为原始签密者的公私钥对;(Nb,pb,qb)为代理签密者的公私钥对;(Nv,pv,qv)为验证者的公私钥对;(N0,p0,q0)为代理公私钥对。

4.1 身份储存算法
原始签密者发出需要Bob代理签密的请求,Bob向原始签密者证明自己的身份。

并利用自己的私钥pb,qb计算:

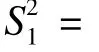
4.2 委托算法
Alice确定Bob的身份后,生成委托信息,发送委托信息给Bob,授予Bob签密权利。

并利用自己的私钥pa,qa计算:

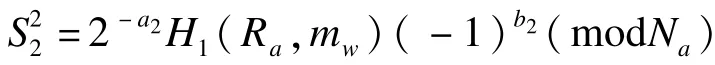
4.3 代理签密算法
如果消息符合委托信息的约定,Bob利用委托信息进行代理签密。
首先,Bob计算x≡S2modpb,并令p0为与x右相邻,且满足p0≡3mod8的大素数,q0=qb≡7mod8,其中,p0,q0为代理私钥,并且令N0=p0q0。则N0作为代理公钥。其次,Bob随机选取,计算T=t2modNv,C=Enct(m),Z=t·S2·C·YpmodNv(Yp从授权信息中获得)。并且分别计算a0,b0的值:
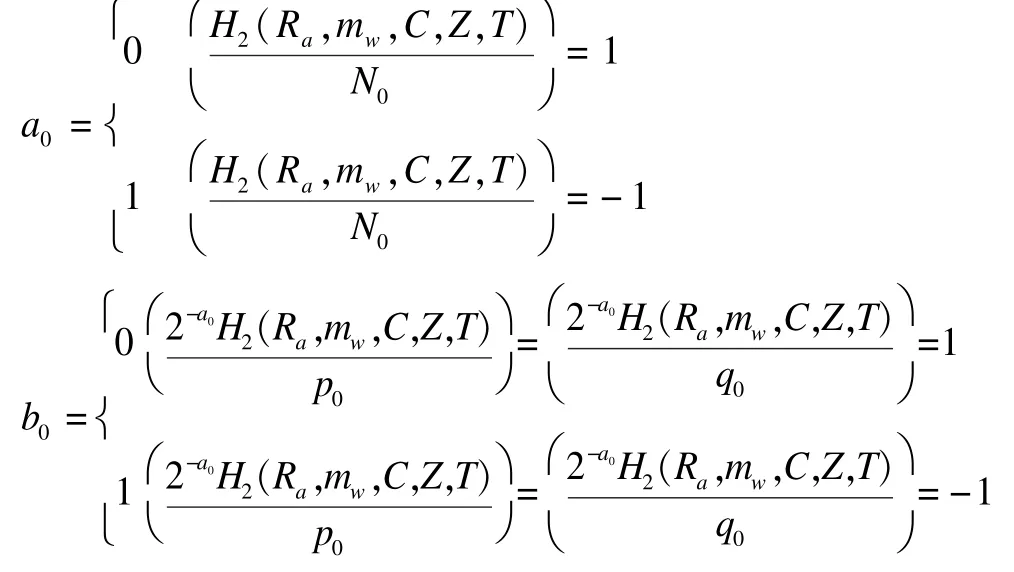
利用代理签密私钥p0,q0计算:
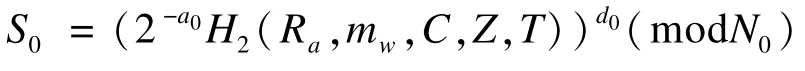
4.4 解签密算法
Verifier对收到的签密消息进行验证。首先, Verifier检查代理签密是否符合代理委托信息mw的约定。如果符合,则进行下一步。若不符合,则拒绝此签密结果。然后,Verifier计算:

Verifier检验h1=H2(Ra,mw,C,Z,T′)是否成立。若成立,则进行下一步。Verifier通过自己的私钥(pv,qv),首先利用中国剩余定理恢复出密钥t,再利用对称加密算法Dect(m)恢复出消息m,如果消息与需要签密的消息一致,那么接受签密结果,否则拒绝。
4.5 揭示代理签密者身份的算法
当验证者对代理签密结果有争议时,可通过原始签密者揭示代理签密者的身份。

5 方案的安全性验证
公开验证性:

由上式可看出,任何人都可以验证该签密结果的有效性。因此,方案具有公开验证性。

在证明过程中,构造一个算法B,B的任务是解决因式分解实例,即给定一个输入N=p×q,以不可忽略的概率输出p,q。证明中,B模拟C与A2进行交互。由于A2这种类型的敌手拥有代理签密者的公私钥对,因此他能给出任意的身份信息,故身份存储算法将不再需要。B运行A2作为子程序,回答A2的询问。


(2)委托询问:A2可以在任何时候进行至多qw次委托询问。当B收到A2关于委托信息mwi发的委托询问时,B首先在H1列表上搜寻(Rai,mwi,S2i,a2i,b2i,h1i),若存在,则返回(Rai,mwi,S2i,a2i,b2i)给A2。否则,B将如同在H1查询中一样,在H1列表中添加包含委托信息mwi的新项,并将(Rai,mwi,S2i,a2i,b2i)发送给A2。

(4)代理签密询问:A2可以在任何时候进行至多qps次代理签密询问。当B收到A2对代理签密的询问时,B首先会从H1列表上查询符合消息mi的委托信息mwi是否存在(Rai,mwi,S2i,a2i,b2i,h1i)上,并且(Rai,mwi,S2i,a2i,b2i,h1i)是否出现在H1列表上。如果没有,B将如同在H1查询中一样在H1列表中添加包含委托信息mwi的新项。B得到与委托信息mwi相对应的值(S2i,a2i,b2i)和随机值Rai。由于A2有代理签密者的私钥(pb,qb),因此A2首先通过代理签密算法生成代理签密公私钥对(N0,p0,q0),然后再生成符合委托信息mwi的消息m的有效签密。
下面考虑解决整数分解问题:在随机预言机模型下,B的输出和协议真实执行的输出是不可区分的。因此,通过一系列的培训,A2将以概率ε输出符合委托信息的消息m∗的有效代理签密。如果敌手没有询问,那么σ∗为有效的概率小于,因为回答H1哈希函数是随机选取的。因此,A2在询问H1预言机后会以概率输出一个有效代理签密。为了分解N,方案利用文献[15-16]的重放攻击技巧,让B重新与A2进行第2次交互。每次交互中,至多进行qw次委托询问。第2次交互与第1次交互的输入完全相同,且对每次的回答也与第1次相同。直到对第i点进行查询,停止输出,重新均匀选择,输出。如果A2在第2次交互后能输出一个有效签密,那么B就可以得到一对签密,和。故可以得到的概率为,所以的概率为。并且可以以的概率使得为N的一个非平凡因子。
对于指定相同输入,2次游戏得到的签密都是基于第i点的,根据文献[17]通用分叉引理的结论,可得基于第i点查询的概率为:而第i点恰好为伪造签密的委托信息的概率为,故可得到分解N的概率为:


定理5 在ROM中,如果存在一个第3类型的敌手A3,在概率多项式时间内以不可忽略的概率ε在定义6中的游戏获胜,那么存在一个算法B利用

定理5的证明方法与定理4类似。由于篇幅有限,这里将不再证明。
6 结束语
本文将代理者签密与身份隐藏进行有效结合,构造一种基于二次剩余的匿名代理者签密方案。分析结果表明,该方案具有不可伪造性。今后将研究方案的保密性,并在抗泄漏的条件下对其进行改进,从而进一步提高其应用性能。
[1] Zheng Yuliang.Digital Signcryption or How to Achieve Cost(Sign-ature&Encryption Cost)<<Cost(Signature)+Cost(Encryption)[C]//Proceedings of the 17th Annual International Cryptology Conference.Santa Barbara,USA:[s.n.],1997:165-179.
[2] Steinfeld R,Zheng Yuliang.A Signcryption Scheme Based on Integer Factorization[C]//Proceedings of the 3rd International Workshop on Information Security. Wollongong,Australia:[s.n.],2000:131-146.
[3] Li Fagen,TsuyoshiT.SecureIdentity-based Signcryption in the Standard Model[J].Mathematical and Computer Modelling,2013,57(11/12):2685-2694.
[4] Pang Liaojun,Li Huixian,Gao Lu,et al.Completely Anonymous Multi-recipient Signcryption Scheme with Public Verification[J].PLOS One,2013,8(5).
[5] Gamage G,LeiwoJ,ZhengYuliang.AnEfficient Scheme for Secure Message Transmission Using Proxy Signcryption[C]//Proceedings of the 22nd Australasian Computer Science.Berlin,Germany:[s.n.],1999: 420-431.
[6] 王 琴.一种基于身份的代理签密体制[J].计算机工程,2011,37(19):120-121,125.
[7] 王会歌,王彩芬,曹 浩,等.无证书代理重签密方案[J].武汉大学学报:理学版,2012,(4):370-376.
[8] 邱卫东,陈克非,白英彩.新型Rabin签名方案[J].软件学报,2000,11(10):1333-1337.
[9] Qiu Weidong,Chen Kefei.Identity Oriented Signature Scheme Based on Quadratic Residues[J].Mathematics and Computation,2005,168(1):235-242.
[10] Clifford C.An Identity Based Encryption Scheme Based on Quadratic Residues[C]//Proceedings of the 8th IMA International Conference on Cryptography and Coding. Cirencester,UK:[s.n.],2001:360-363.
[11] 柴震川,董晓蕾,曹珍富.利用二次剩余构造的基于身份的数字签名方案[J].中国科学,2009,39(2): 199-204.
[12] Yu Yong,Mu Yi,Susilo W.Provably Secure Proxy Signature Scheme from Factorization[J].Mathematics and Computation Modelling,2012,55(3/4):1160-1168.
[13] 谷利泽,张 胜,杨义先.一种新型代理签密方案[J].电子与信息学学报,2005,27(9):1463-1466.
[14] Jonathan K,LindellY.IntroductiontoModern Cryptography[M].New York,USA:Chapman&Hall/ CRC,2008.
[15] Pointcheval D,Stern J.Security Arguments for Digital Signatures andBlindSignatures[J].Journalof Cryptology,2000,13(3):361-396.
[16] Pointcheval D,Stern J.Security Proofs for Signatures Schemes[EB/OL].(2012-12-20).http://www.di.ens.fr/ users/pointche/Documents/Papers/2000_joc.pdf.
[17] Bellare M,NevenG.Multi-signaturesinthePlain Public-key Model and a General Forking Lemma[C]// Proceedings of the13th Association for Computing Machinery Conference on Computer and Communications Security.Alexandria,USA:[s.n.],2006:390-399.
编辑 刘 冰
Anonymous Proxy Signcryption Scheme Based on Quadratic Residue
LIU Zhen1,YANG Qiliang2,YANG Bo1
(1.School of Computer Science,Shaanxi Normal University,Xi’an 710062,China;
2.College of Informatics,Shu-Te University,Kaohsiung 82445,Taiwan,China)
Most of the existing signcryptions are based on bilinear pairing,but the signcryption without bilinear pairing is a research of cryptography,because the pairing operation requires a lot of computations,and it can not anonymous the proxy signcrypter.The signature scheme based on quadratic residue is widely used with its advantages such as simple description,resistance of chosen ciphertext attack and high efficiency.Its efficient is higher compared with signcryption schemes based on bilinear pairing.This paper adds anonymity to the scheme based on quadratic residue to realize anonymous proxy signcryption.Analysis results show that the scheme not only provides anonymity,but also provides public verifiability.
proxy signcryption;anonymity;quadratic residue;random oracle model;public verification;traceability; non-repudiation
刘 祯,杨启良,杨 波.基于二次剩余的匿名代理者签密方案[J].计算机工程,2015,41(2):129-134,140.
英文引用格式:Liu Zhen,Yang Qiliang,Yang Bo.Anonymous Proxy Signcryption Scheme Based on Quadratic Residue[J].Computer Engineering,2015,41(2):129-134,140.
1000-3428(2015)02-0129-06
:A
:TP309.7
10.3969/j.issn.1000-3428.2015.02.025
国家自然科学基金资助项目(61272436,61370224);广东省自然科学基金资助项目(10351806001000000)。
刘 祯(1989-),女,硕士,主研方向:信息安全,密码学;杨启良,学士;杨 波,教授。
2014-02-24
:2014-04-14E-mail:liuzhen0227@126.com
