基于中国剩余定理的无可信中心可验证秘密共享研究
2015-01-06朱晓玲
杨 阳,朱晓玲,丁 凉
(合肥工业大学计算机与信息学院,合肥230009)
基于中国剩余定理的无可信中心可验证秘密共享研究
杨 阳,朱晓玲,丁 凉
(合肥工业大学计算机与信息学院,合肥230009)
基于中国剩余定理提出一种无可信中心可验证门限签名秘密共享方案。该方案无需可信中心的参与,每个成员被视为分发者,通过相互交换秘密份额影子协同产生各自的秘密份额,从而避免可信中心的权威欺骗。成员利用自己的秘密份额产生部分签名,再由部分签名合成组签名,在签名过程中不直接利用或暴露组私钥,从而保证组私钥的可重用性。基于离散对数求解困难性,构造秘密份额影子验证式,从而识别成员之间的欺骗行为,有效防止成员之间的恶意欺诈。实验结果表明,与基于拉格朗日插值的秘密共享方案相比,该方案具有较高的计算效率。
秘密共享;可信中心;可验证;门限签名;中国剩余定理;离散对数问题
1 概述
1979年,Shamir[1]和Blakley[2]分别基于Lagrange Interpolation定理和射影定理,提出2种(t,n)门限秘密共享方案。随后,人们对门限秘密共享进行了广泛研究。文献[3]基于离散对数问题,提出了一种非交互式可验证秘密共享方案,该方案通过验证等式而无需信息交互,能够验证和识别假的秘密份额,但攻击者可能获得秘密构造多项式。文献[4]对文献[3]的方案进行改进,基于同态承诺提出一种非交互可验证秘密共享方案,能够保证秘密构造多项式的安全。为了避免可信中心的“权威欺骗”,1994年,文献[5]基于Lagrange Interpolation提出一种无可信中心门限签名方案,但是该方案经过一次签名后,攻击者容易获得组私钥和成员的私钥,导致私钥不可重用。文献[6]采用联合秘密共享技术解决了成员私钥易被恢复的问题。文献[7]基于Lagrange Interpolation提出一种无可信中心的有向门限签名方案,但不能验证成员提供的秘密份额的真实性。文献[8]基于Lagrange Interpolation提出一种无可信中心动态秘密共享方案,该方案在不暴露共享秘密的情况下,通过成员协同交互,能够动态地更新各自的秘密份额,增加新成员,但其计算量大。
文献[9]提出一种基于中国剩余定理(Chinese Remainder Theorem,CRT)的秘密共享方案,与基于Lagrange Interpolation方案相比,其计算量较小。文献[10-11]基于CRT分别提出2个可验证秘密共享方案(VSS),但上述2种方案均需可信中心产生和分发秘密份额。文献[12]基于CRT提出了一种新的VSS方案并证明了其安全性,该方案中由成员协同产生秘密份额,但其验证过程仍需要一个可信中心参与。文献[13]基于CRT提出一种可验证的秘密共享方案,该方案由可信中心与成员合作产生秘密份额与验证信息,其验证信息较文献[12]更简单。文献[14]提出一种无可信中心门限签名方案,该方案没有对秘密份额进行验证,在交互过程中,成员之间可能存在欺骗行为。目前,基于CRT的可验证无可信中心门限秘密共享方案尚未发现。
本文基于CRT提出一种可验证的无可信中心门限签名方案,该方案无需可信中心,所有成员相互合作,在不泄露秘密的情况下产生秘密份额及组公钥并隐式产生组私钥。此外,本文方案成员相互协作产生验证参数,通过验证等式验证秘密份额的真实性。
2 Asmuth-Bloom方案
2.1 初始化
假设DC是一个分发者,P={P1,P2,…,Pn}是n个成员组成的集合,门限为t,秘密是S。DC选取一个大素数q(q>S),整数A和一个正整数序列d= {d1,d2,…,dn},且满足以下条件:
(1)0≤A≤[N/q]-1;
(2)d1,d2,…,dn严格单调递增;
(3)(di,dj)=1,(i≠j);
(4)(di,q)=1,(i=1,2,…,n);
2.2 秘密分割
DC计算:

并发送(zi,di)给Pi(i=1,2,…,n)作为Pi的秘密份额。
2.3 秘密恢复
任何成员可以通过相互交换各自的秘密份额恢复秘密S。设W={P1,P2,…,Pt}为恢复秘密的一组t个成员。相互交换秘密后,Pi(i=1,2,…,t)可以构建如下同余方程组:

根据CRT,该方程组有唯一解z:

则秘密S为:

Asmuth-Bloom方案基于中国剩余定理,计算量较小,但需一个可信中心的参与,且无法验证成员秘密份额的真实性。
3 本文方案
本文基于CRT,提出一种新的可验证的无可信中心门限签名方案。与基于Lagrange Interpolation的门限签名方案相比,具有较高的计算效率。
本文方案分为3个步骤:(1)秘密份额与组密钥的产生;(2)部分签名的产生;(3)合成和验证签名。
3.1 秘密份额与组密钥的产生
假设P={P1,P2,…,Pn}是一组n个成员的集合,门限值为t。选取公共参数:2个大素数p和q,一组正整数序列d={d1,d2,…,dn}和一个素数域上的生成元g,q和d满足Asumth-Bloom方案。公开n,t,p,q,g和d={d1,d2,…,dn}。
(1)Pi(i=1,2,…,n)随机选择yi和一个整数Ai满足以下条件:

Pi计算:

其中,yi表示成员的子秘密,即成员私钥;aij为秘密份额影子,用于产生秘密份额。
公开aij(i≠j),gAi和gyi,Pi保存aii。
(2)Pi计算组公钥Y:

尽管成员Pi公开gyi,但通过gyimodp求yi属于离散对数问题,因此成员私钥yi不会泄漏。另一方面,通过Y求:

也属于离散对数问题;因此,除非所有成员合作,否则任何人无法获得组私钥X。
(3)Pi计算αi,βij(j=1,2,…,n):

并广播αi,βij。
当收到Pi发送来的aij之后,Pj可以通过下式验证秘密份额影子aij的正确性:
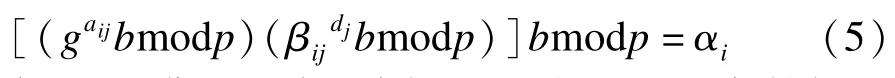
如果aij满足上式,则成员Pi发送的秘密份额影子aij为真。
定理1秘密份额验证式(2)~式(5)正确。
证明:

定理2Pi无法公布假的gAi。
证明:假设Pi公布一个假的gAi设为Fi,即当Pj收到Fi后,式(4)、式(5)仍然成立。设a′ij为Pi提供的假的秘密份额影子,因此:
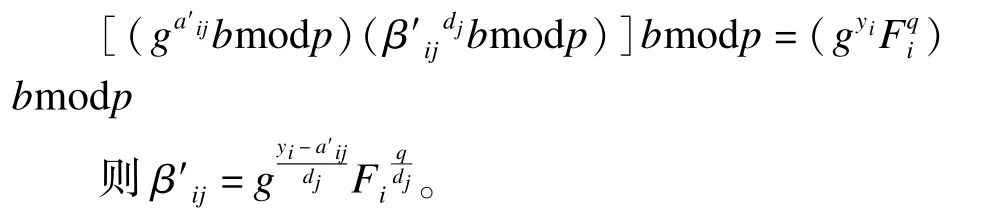
由于g和q是2个素数,如果Fi不是g的幂,βij将不是整数,与方案中条件βij=gkijmodp必为整数相矛盾。因此,Fi必是g的幂。假设:

由于β′ij是一个整数且g是一个素数,因此:

另一方面,秘密份额值小于dj,因此:

完全符合方案初始构造秘密份额影子条件,即a′ij为真,与假设a′ij为假秘密份额相矛盾。
因此,Pi无法公布假的gAi。
定理3Pi无法提供假的αi。
证明:为了计算公钥,Pi必须提供真的gyi。另一方面,Pi无法提供假的gAi。因此,αi可以通过下式验证:

如果αi满足上式,αi为真。否则,αi为假。
因此,Pi无法提供假αi。
定理4Pi无法提供假βij。
证明:假设Pi公开假β′ij≠βij,由于αi为真,即当Pj接受a′ij≠aij时,式(3)~式(5)仍然成立。
因此:


由于秘密份额的值比dj小,因此a′ij>dj恒不成立。
因此,Pi无法提供假βij。
(4)当收到其他成员的aij后,Pj计算他的秘密份额Lj:

成员Pj可利用Lj产生自己的部分签名。
3.2 部分签名的产生
t个成员利用各自的秘密份额,基于CRT产生各自的部分签名,并发送给签名合成者。
(1)Pi选取任意随机数ui∈Zq,计算并广播ri:
(2)Pi计算:

ei可以通过下式计算:

Vi用于计算部分签名。由于成员Pi在计算Vi时需用到自己的秘密份额Li,因此每个成员只能产生自己的部分签名。
(3)Pi为报文M产生各自的部分签名并发送(M,r,si)给签名合成者。

3.3 合成与验证签名
合成者收到t个部分签名(M,r,si)后,计算:

(M,r,s)是报文M的组签名。任何人均可利用组公钥验证签名。验证式如下:

如果上式成立,则组签名(M,r,s)有效。
定理5(正确性分析) 如果gs≡rM·Yrmodp,组签名(M,r,s)有效。
证明:假设:

t个成员P1,P2,…,Pt各自拥有秘密份额L1,L2,…,Lt,满足下面同余式:
Z≡Limoddi,i=1,2,…,t(10)
通过式(1)和式(2):

另一方面,通过式(3)和式(9),可以得到:

因此:




根据式(2)~式(7):

另一方面,由式(4)和式(11),得:



4 安全性分析
本文方案安全性分析如下:
(1)本文方案无需可信中心,秘密份额由全体成员协同产生,任何人均无法知道组私钥,有效地避免了可信中心的权威欺骗。
(2)本文方案能够识别成员之间的欺诈行为,根据定理2~定理5,每个成员必须公开真的αi,βij,如果Pi提供假的秘密份额影子aij,通过αi,βij及验证式(2)~式(5)可以检测出来。
(3)组私钥X是安全的且具有可重用性。在组密钥产生阶段,除非全体成员合作,单个成员无法获得组私钥X(由式(2)~式(4)可知)。在部分签名产生阶段,每个成员计算部分签名si=ui·M+r·Vi时没有直接使用或暴露组私钥X的任何信息,因此,在一次签名后,组私钥仍可以重复使用。
(4)在验证过程中,各成员子秘密yi是安全的。本文方案在验证aij过程中需要每个成员Pi公开验证信息:

根据αi求得Xi属于离散对数问题,因此αi是安全的,另一方面,攻击者想根据βij获得Xi,则必须知道kij,而根据kij获得βij仍然属于离散对数问题。因此,Xi是安全的,进而yi(yi=Xi-Aiq)也是安全的。
5 方案实例
本节通过实例验证本文方案的正确性。
(1)初始化条件:假设n=5,t=3,p=13,q=11,g=3,d={9,11,13,15,17}和M=1。
(2)秘密份额及组公钥的产生:


(3)验证秘密份额影子:
如果P1提供真的秘密份额影子a12=1,则:

因此成员之间的欺骗行为可通过式(2)~式(5)识别。
(4)部分签名产生:

P1的部分签名为(1,1,859),并发送给签名合成者。
P2计算部分签名:

P2的部分签名为(1,1,118),并发送给签名合成者。
P3计算部分签名:

P3部分签名为(1,1,496),并发送给签名合成者。
(5)组签名的合成与验证:

则(1,1,10)为报文M的组签名。
验证组签名:

因此:

即组签名是正确的。
6 实验结果与分析
实验环境:实验平台为Lenovo PC,T420i, Intel(R),Core(TM)i3-2310M,2.1GHz。操作系统为Win7,开发软件为Microsoft Visual C++6.0。
实验目的:测试本文方案和基于Lagrange Interpolation门限签名方案中产生部分签名的时间消耗。
实验方案:Harn无可信中心签名方案[5]是一种经典的基于Lagrange Interpolation无可信中心门限签名方案,故测试该方案部分签名产生的时间消耗,并与本方案对比。文献[5]中部分签名计算如下:

其主要时间消耗为计算拉格朗日插值基函数:

在本文方案中,部分签名计算如下:

其主要时间消耗为计算逆元ei。
(1)测试基于Lagrange Interpolation门限签名方案部分签名时间消耗。基于Lagrange Interpolation门限签名方案中,成员数n为15,秘密份额集合X={10,11,12,13,14,15,16,17,18,19,20, 21,22,23,24}对应成员集合P={P1,P2,…,P15};门限t分别取3,4,5,6,7,8,9,10。当t=3时,选取成员P1,P2,P3;当t=4时,选取P1,P2,P3,P4;依此类推。测试P1产生部分签名时间消耗。实验结果如表1所示。

表1 基于Lagrange Interpolation方案的部分签名时间消耗
(2)测试本文方案部分签名时间消耗。本方案中,取成员数n为15,成员集合为P={P1,P2,…,P15},门限t分别取3、4、5、6、7、8、9、10。选取序列d={3,7,11,17,19,23,29,31,37,41}为对应{P1,P2,…,P10}的模;当t=3时,选取成员P1,P2,P8;当t=4时,选取P1,P2,P3,P8;依此类推。测试P8产生部分签名时间消耗。实验结果如表2所示。

表2 本文方案部分签名时间消耗
如图1所示,本文方案计算部分签名时间远少于基于Lagrange Interpolation门限签名方案,故本方案的时间效率优于基于Lagrange Interpolation门限签名方案。

图1 部分签名时间的消耗对比
7 结束语
本文基于CRT提出一种可验证的无可信中心门限签名方案。本文方案无需可信中心,成员通过交换秘密份额影子协同产生各自的秘密份额,从而避免了可信中心的“权威欺骗”,并能够识别成员之间的欺骗行为。成员利用各自的秘密份额产生部分签名,再由部分签名合成组签名;在签名过程中没有直接利用或暴露组私钥,从而保证了组私钥的可重用性。本文对方案的正确性和安全性进行了理论分析,并通过实例验证方案的正确性。
[1] Shamir A.How to Share a Secret[J].Communications of ACM,1979,22(11):612-613.
[2] Blakley G R.Safeguarding Cryptographic Keys[C]// ProceedingsofNationalComputerConference. Arlington,USA:[s.n.],1979:313-317.
[3] Feldman P.APracticalSchemeforNon-interactive Verifiable Secret Sharing[C]//Proceedings of the 28th IEEE Symposium on Foundations of Computer Science. [S.1.]:IEEE Computer Society,1987:427-437.
[4] Pedersen T P.Non-interactiveandInformation-theoretic Secure Verifiable Secret Sharing[C]//Proceedings of the 11thAnnualInternationalCryptologyConferenceon Advances in Cryptology.[S.1.]:IEEE Press,1991: 129-140.
[5] Harn L.Group-oriented(t,n)ThresholdDigital Signature Scheme and Digital Multisignature[J].IEEE Proceedings of Computers and Digital and Techniques, 1994,141(5):307-313.
[6] 王 斌,李建华.无可信中心的(t,n)门限签名方案[J].计算机学报,2003,26(11):1581-1584.
[7] 沈忠华,于秀源.一个无可信中心的有向门限签名方案[J].杭州师范学报:自然科学版,2006,5(2): 95-98.
[8] 何二庆,侯整风,朱晓玲.一种无可信中心动态秘密共享方案[J].计算机应用研究,2013,30(2):177-179.
[9] Asmuth C A,Bloom J.A Modular Approach to Key Safeguarding[J].IEEE Transactions on Information Theory,1983,29(2):208-210.
[10] Li Qiong,Wang Zhifang,Niu Xiamu,et,al.A Aoninteractive Modular Verifiable Secret Sharing Scheme[C]// Proceedings of International Conference on Communications,Circuits and Systems.Los Alamitos,USA:[s.n.], 2005:84-87.
[11] Iftene S.Secret Sharing Schemes with Applications in Security Protocols[D].[S.1.]:UniversityAlexandru,2007.
[12] Kaya K,Selcuk A A.A Verifiable Secret Sharing Scheme BasedontheChineseRemainderTheorem[C]// Proceedings of the 9th Annual International Conference on Cryptology.Kharagpur,India:[s.n.],2008:414-425.
[13] 于 洋,刘焕平.可验证的Asmuth-Bloom秘密共享方案[J].哈尔滨师范大学学报:自然科学版,2012, 28(3):20-23.
[14] 侯整风,李汉清,胡东辉,等.基于中国剩余定理的无可信中心门限签名方案[C]//2011中国仪器仪表与测控技术大会论文集.北京:中国仪器仪表学会,2011.
编辑 索书志
Research on Verifiable Secret Sharing Without Trusted Center Based on Chinese Remainder Theorem
YANG Yang,ZHU Xiaoling,DING Liang
(School of Computer and Information,Hefei University of Technology,Hefei 230009,China)
A new verifiable threshold signature scheme without a trusted center is proposed based on Chinese Remainder Theorem(CRT).The scheme do not needed the trusted center.Each participant is regarded as a distributor,and generates his own secret share by exchanging secret share shadows with the others,which can avoid the trusted center’s authority deception.Participants use their own secret shares to generate the partial signatures,and the group signature is composed of the partial signatures,which means the group private key is not used or exposed directly,so that the group private key’s reusability can be ensured.Based on the discrete logarithm problem,the scheme constructs the secret shadow verification formula,so that it can identify the participants’mutual cheating to prevent the malicious fraud of the participants effectively.Experimental results show that compared with the secret sharing schemes based on Lagrange interpolation,this scheme is more efficient.
secret sharing;trusted center;verifiable;threshold signature;Chinese Remainder Theorem(CRT);discrete logarithm problem
杨 阳,朱晓玲,丁 凉.基于中国剩余定理的无可信中心可验证秘密共享研究[J].计算机工程, 2015,41(2):122-128.
英文引用格式:Yang Yang,Zhu Xiaoling,Ding Liang.Research on Verifiable Secret Sharing Without Trusted Center Based on Chinese Remainder Theorem[J].Computer Engineering,2015,41(2):122-128.
1000-3428(2015)02-0122-07
:A
:TP309
10.3969/j.issn.1000-3428.2015.02.024
广东省教育部产学研结合基金资助项目(2008090200049)。
杨 阳(1991-),男,硕士研究生,主研方向:信息安全;朱晓玲,博士研究生;丁 凉,讲师。
2014-03-19
:2014-04-14E-mail:yangyang9074@163.com
