用于保护位置隐私的邻近检测算法

张一帆,尹树祥

(复旦大学计算机科学技术学院,上海200433)

用于保护位置隐私的邻近检测算法

张一帆,尹树祥

(复旦大学计算机科学技术学院,上海200433)

现有保护位置隐私的邻近检测算法通常根据网格大小对用户位置进行量化计算,会降低算法结果的准确性。针对该问题,提出2种准确安全的邻近检测算法。用户将自己的位置分成网格内坐标以及网格编号两部分,并将其分别加密后发送给服务器,服务器利用加密后的网格内坐标在整个地图中筛选出所有满足查询的网格,用户根据服务器的返回结果判断用户之间是否邻近。实验结果表明,算法1速度快,传输信息少,算法2更加安全,但计算和通信开销较大,并且需查询与被查询用户同时在线。用户可根据对服务器的信任程度、查询性能和应用场景需求进行算法选择。

基于位置的服务;隐私保护;安全;加密;邻近检测;位置隐私

1 概述

随着拥有定位功能的移动设备(主要是智能手机)的普及,基于位置的服务已经广泛应用于交通、物流、医疗、生活等领域中[1]。用户可以通过共享当前的位置信息来享用各种服务。邻近检测是一种典型的服务:当2个朋友间的距离在某个范围内时,应用会发出通知提醒用户。

现有基于位置的服务要求用户共享他们的确切位置,这使得用户隐私保护问题成为阻碍市场发展的一个重要因素。如果这些服务不能提供一定程度的隐私保护,用户可能不共享他们的位置,这样用户也无法从这些基于位置的服务中获得便利。然而,保护位置隐私与享受服务之间存在矛盾:位置信息越精确,服务质量越高,隐私度越低[2]。

针对邻近检测问题,国内外学者提出了一些方法[3-4],使得朋友之间可以无需将确切位置暴露给服务提供商以及对方的条件下,即可判断对方是否在自己附近。文献[5]先运用保持距离不变的映射函数对用户位置加密,再计算加密后位置间的距离。然而,文献[6]指出这种保持距离不变的映射函数不安全,攻击者可以轻易破解映射函数。更多的学者倾向于采用基于网格的方法。基于网格的方法通常将整个地图划分为许多网格,用户将自己所处的网格编号进行加密,服务器通过比较用户所在的网格是否相同来判断他们是否邻近。文献[7]将整个地图划分成互相重叠的六边形网格,然后通过比较用户所处的3个网格中是否有相同的网格来判断用户是否邻近。但是此类方法不够灵活,用户只能采用预先设定的距离进行查询。文献[8]采用多层次的网格,并提出邻近区域的概念,使得用户可以任意指定查找范围而不仅局限于他们之间的空间距离。但是该方法同样存在以下问题:多层次的网格使得用户需要经过多次通信协议才能得到检测结果,增加算法的整体运行时间。另外,文献[9]采用剪枝和精炼的方法,但难以保证计算结果的准确性。

为解决上述问题,本文提出2种保护用户隐私同时能够得到准确检测结果的邻近检测算法。先将地图划分成网格,再将用户的位置分成网格内的坐标以及网格编号两部分,这样使得服务器在不知道用户确切位置的情况下也能够准确判断用户间是否邻近。

2 问题描述

2.1 系统模型

本文考虑针对2个不同实体的邻近检测服务:拥有可定位和网络通信的移动设备的用户可以确定自己的位置并连接到服务器;服务提供商接收用户发来的请求与位置信息,判断用户之间是否邻近,并进行相应的通知。

问题定义:用户A与用户B是朋友;用户B周期性地将自己的位置加密后发送给服务器;用户A将查询请求以及自己的位置信息发送给服务器;服务器根据用户A与用户B的位置信息进行计算。当用户A与用户B之间的距离小于用户A设定的阈值R时,用户A将收到通知。

2.2 设计目标

在理想模型下,算法应该满足以下条件:

(1)不对称性:用户A了解用户B是否在附近,而用户B不知道任何信息;

(2)距离阈值:阈值R由每个用户设定且不统一;

(3)安全性:用户A只知道用户B是否在其附近,而用户B和服务器不知道任何信息;

(4)准确性:判断结果尽量准确,如果存在误差,则控制在一定范围内,并且用户可以决定该范围的大小;

(5)性能:由于应用运行在资源有限的移动设备上,需要考虑到算法在计算和通信上的开销。

3 邻近检测算法

在现有基于网格的算法中通常存在一些区域,系统不能准确判断用户的邻近关系,造成这个不确定区域的原因在于,用户通过网格将自己的位置信息隐藏起来,但与此同时也模糊了自己的位置,使得系统不能准确进行判断。为此,本文提出2种能够得到准确检测结果的异步邻近检测算法(算法1)和同步邻近检测算法(算法2)。

3.1 异步邻近检测算法

3.1.1 异步邻近检测算法描述

将地图划分成边长为a的网格,将用户U在网格内的坐标记为Lx(U),Ly(U),网格在水平方向和垂直方向的坐标记为Gx(U),Gy(U)。

假设用户A与用户B是好友,并且共享一个密钥k。同时,他们各自维护一个初始值为零的计数器ctr。

用户B增加计数器ctr,并且通过密钥k和计数器ctr生成随机数(r1,r2,r3,k1,k2,k3,k4)←F(k,ctr),然后计算:

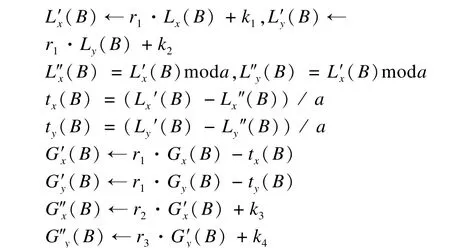
用户A向服务器询问用户B的计数器数值。如果服务器返回值是用户A曾经使用的,那么查询中止。用户A用密钥k和计数器ctr生成随机数,然后用相同方法加密自己的位置信息,并将加密后的信息与距离阈值R′←r1·R一起发送给服务器。

服务器收到用户A的请求后,找到与用户A具有相同计数器值ctr的用户B的位置信息,然后计算所有满足(L″x(A)-L″x(B)+na)2+(L″y(A)-L″y(B)+ma)2≤R′2的(n,m)值,其中,n,m是整数,服务器得到一系列(n,m)值。这里需要注意的是只有那些在边界处的(n,m)值才需被记录。服务器通过用户的网格坐标信息判断他们的相对位置,并为每一对(n,m)值计算:

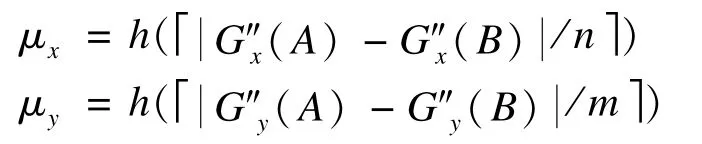
其中,x表示不小于x的最小整数;h(·)是一个保持顺序的哈希函数。最后,服务器将{(μx,μy)}列表作为结果发送给用户A。

用户A收到服务器的结果后,判断是否有(μx,μy)满足。如果有这样的(μx,μy)存在,那么用户A认为用户B与自己邻近。

3.1.2 异步邻近检测算法分析

算法分析具体如下:

(1)性能

在算法1中采用异步的方法,因此在查询过程中,无需向用户B询问其位置信息。同时,通过(n,m)列表对所有满足条件的网格进行压缩,减少了算法通信开销。在整个算法运行过程中,只需要进行简单的加法、乘法运算以及哈希函数的映射,使得算法能够快速运行。

(2)安全性

在整个算法运行过程中,用户B不知道任何信息;服务器知道用户A与用户B加密后的位置信息。虽然服务器能够通过比较的值,并进一步知道用户A与用户B的相对位置(比如用户A在用户B的西南方)。但是服务器并不能通过这些信息进一步了解用户所在的区域以及他们的确切位置,因此,算法仍然是安全的。

由于用户A可能通过移动并利用三角法则来确定用户B的位置,因此允许用户B用一个参数来保护确切位置。当用户B在发送位置信息时,在一个预先设定的范围内生成一个随机数d,并发送d′=r1d作为距离参数。当服务器收到用户A加密了的位置信息和距离阈值后,计算R″=R′+d′,并作为查询范围。由于用户A不知道随机数d的值,因此不能确定用户B的确切位置。需要注意的是增加这样该参数可能会导致检测结果不准确,但是这个不确定的区域大小仅随着该参数改变,与网格大小无关。

3.2 同步邻近检测算法

在算法1中,用户将他们的相对位置暴露给服务器。如果假定服务器在得知用户A的加密网格坐标后,可以计算与A相邻的网格坐标的加密信息,那么可以使服务器计算所有满足查询的网格坐标的密文,然后运用安全相等测试[10-13],让用户A来判断用户B是否落在这些网格内。这样服务器就不能知道任何信息(包括用户的相对位置),但计算开销会有所增加。

3.2.1 同步邻近检测算法描述

假设G是一个p阶的循环群,其中,p是质数;g是G的一个生成元。

用户A在Zp中选择一个随机数x,并计算h←gx,这样可以生成私钥{x},公钥{g,h}。

与算法1一样,用户B增加计数器ctr,生成随机数,计算并发送自己加密后网格内的坐标信息。

用户A查询计数器ctr,同样加密自己网格内的坐标,并计算作为自己加密后的网格信息:

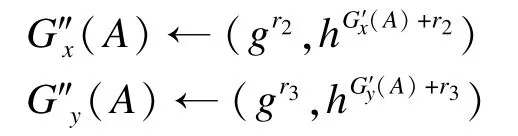
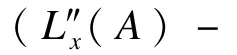
3.2.2 同步邻近检测算法分析

算法分析具体如下:

(1)邻居数量

在该算法中,服务器不再知道用户A与用户B的相对位置。但是,由于服务器和客户端都需要计算和传输所有满足查询的网格加密后的信息,计算开销与通信开销都有所增加。这些额外开销取决于邻居数量,因此,一个合适的网格大小非常重要。

(2)安全性

尽管在该算法中,服务器不知道任何信息,但是客户端知道邻居数量。为防止这个可能的安全隐患,服务器可以在计算用户A的邻居加密信息时增加一些虚假信息。如果给定一个距离阈值,那么邻居的最大数量N可以确定。因此,如果服务器每次都传输N个网格信息给用户B,其中包括一些虚假的信息,那么用户B就不知道邻居的真正数量。

本文提出2种新的邻近检测算法,将用户的位置分为网格内坐标以及网格编号两部分,通过让服务器根据用户的网格内坐标,在地图上筛选出所有满足查询的网格,再进一步对这些网格进行比较,得到准确的检测结果。

本文提出的2种算法:算法1运行速度快,传输信息少,但是会将用户的相对位置暴露给服务器;算法2更加安全,但是计算和通信开销有所增加,并且要求用户同时在线才能进行查询。对于用户如何选择使用哪种算法,取决于用户对于服务器的信赖程度,以及对算法性能与功能上的需求。

4 实验结果与分析

由于该算法部分运行在移动终端上,计算开销与网络通信开销显得异常重要。为测试算法性能,对于不同的参数设置,分别对计算开销和网络通信开销进行实验。实验中地图大小是50 000×50 000, 1个单位代表1m。用户位置由算法随机生成。实验运行在四核1.70 GHz处理器、4 GB内存,运行64位Windows7操作系统的计算机上。算法2采用PBC(Pairing-Based Cryptography)库来实现加密算法,其中,p是160位的质数;g是512位的整数。实验结果均为100次计算后的平均值。

4.1 通信开销

在算法1中,通信开销主要在于服务器返回的(μx,μy)列表。对于不同的网格大小以及查询半径,服务器返回的列表大小如图1所示。随着查询半径的增加,服务器返回列表的大小也随之增加。原因在于增大查询半径会使得更多的网格处于查询范围内,即满足条件的(n,m)值增加,返回列表也由此更大。同时可以看到,网格大小也对返回列表有影响。这是由于网格越大,在查询范围中的网格数量会相应减小。

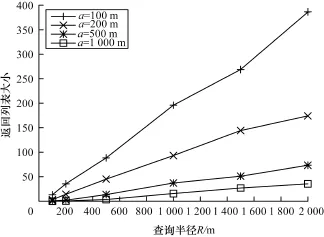
图1 算法1中服务器返回列表大小

网格大小同样会影响安全性。如果网格太大,会使得用户处于少量网格中,那么用户A就有可能通过返回列表的数量来推测用户B的位置。

在算法2中,通信开销取决于满足条件的网格数量,通过在不同参数情况下测试这些网格数量,得到结果如图2所示。可以看出,由于在通信中需要列举出所有满足查询的网格,而不是像算法1中只需要列举出那些处于边界处的网格,因此算法2的通信开销远远大于算法1;同时,网格大小越小、查询半径越大时,网格的数量会有指数级的增长。

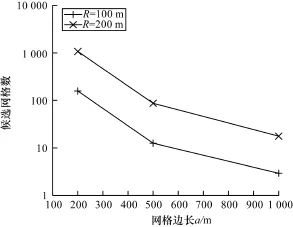
图2 算法2中满足查询的网格数量

4.2 计算开销

由于算法1仅需要一些加法和乘法运算以及哈希函数的映射,运行时间较少,因此在此只讨论算法2。在实验中,通过改变各查询半径以及网格大小,对算法2的计算开销进行评估。

图3和图4分别是查询半径R=100 m与R= 200 m时,在不同网格大小下服务器、用户A以及用户B各自的计算开销。

图3 查询半径R=100 m时算法2的计算开销

图4 查询半径R=200 m时算法2的计算开销

可以看出,网格越小,查询半径越大,那么满足条件的网格就越多,计算开销也越大。另外,用户A的计算开销大于服务器和用户B,这是因为用户A需要对每个服务器返回的候选网格进行运算并判断用户B是否与自己邻近。

5 结束语

本文提出2种准确安全的邻近检测算法。将地图事先划分成网格后,通过将用户的位置分成网格内的坐标以及网格编号两部分,分别对两部分信息进行加密,使得用户在不将自己位置暴露给其他用户和服务器的情况下,准确判断其他用户是否在自己附近。通过实验比较2种算法在不同网格大小以及查询半径下的通信以及计算开销,结果表明,2种算法均能保护用户隐私,同时得到准确的检测结果。今后将从邻近区域的角度出发,进一步研究在非欧式距离以及指定查询区域情况下的邻近检测问题。

[1] 唐科萍,许方恒,沈才棵.基于位置服务的研究综述[J].计算机应用研究,2012,29(12):4432-4436.

[2] 潘 晓,肖 珍,孟小峰.位置隐私研究综述[J].计算机科学与探索,2007,1(3):268-281.

[3] Nielsen J D,Pagter J I,StausholmM B.Location PrivacyViaActivelySecurePrivateProximity Testing[C]//Proceedings of 2012 IEEE International ConferenceonPervasiveComputingandCommunications Workshops.Lugano,Italy:IEEE Press, 2012:19-23.

[4] Narayanan A,Thiagarajan N,Lakhani M,et al.Location Privacy via Private Proximity Testing[C]//Proceedings of NDSS’11.[S.l.]:IEEE Press,2011.

[5] Ruppel P,Treu G,Küpper A,et al.Anonymous User Tracking for Location-based Community Services[C]// Proceedings of the 2nd International Conference on LocationandContext-awareness.Berlin,Germany: Springer-Verlag,2006:116-133.

[6] Liu K,Giannella C,Kargupta H.An Attacker’s View of Distance Preserving Maps for Privacy Preserving Data Mining[C]//Proceedingsofthe10thEuropean Conference on Principle and Practice of Knowledge Discovery inDatabases.Berlin,Germany:Springer-Verlag,2006:297-308.

[7] Siksnys L,Thomsen J R,Saltenis S,et al.Private and Flexible Proximity Detection in Mobile Social Networks[C]//Proceedings of the11th International Conference on Mobile Data Management.Washington D.C., USA:IEEE Computer Society,2010:23-26.

[8] Mascetti S,Bettini C,Freni D,et al.Privacy-aware Proximity Based Services[C]//Proceedings of the10th International Conference on Mobile Data Management: Systems,Services and Middleware.Washington D.C., USA:IEEE Computer Society,2009:31-40.

[9] Saldamli G,Chow R,Jin H,et al.Private Proximity Testing With an Untrusted Server[C]//Proceedings of the 6th ACM Conference on Security and Privacy in Wireless and Mobile Networks.New York,USA:ACM Press,2013:113-118.

[10] Montreuil A,PatarinJ.TheMarriageProposals Problem:Fair and Efficient Solution for Two-party Computations[C]//Proceedings of the 5th International Conference on Cryptology in India.Berlin,Germany: Springer-Verlag,2004:33-47.

[11] Fagin R,Naor M,Winkler P.Comparing Information Without Leaking It[J].Communications of the ACM, 1996,39(5):77-85.

[12] Lipmaa H.Verifiable Homomorphic Oblivious Transfer andPrivateEqualityTest[C]//Proceedingsof ASIACRYPT’03.Berlin,Germany:Springer-Verlag, 2003:416-433.

[13] Naor M,Pinkas B.Oblivious Transfer and Polynomial Evaluation[C]//Proceedings of the 31st Annual ACM Symposium on Theory of Computing.New York,USA: ACM Press,1999:245-254.

编辑 陆燕菲

Proximity Testing Algorithms for Preserving Location Privacy

ZHANG Yifan,YIN Shuxiang
(School of Computer Science,Fudan University,Shanghai 200433,China)

Existing privacy preserving proximity testing algorithms usually quantize user’s location according to grid size,which makes these algorithms have low accuracy.Aiming at this problem,this paper proposes two accurate and secure proximity testing algorithms.A user transforms location to two parts,the coordinates inside the grid and the grid index,and sends them both after encryption.Then the server computes all possible grids which satisfy the query according to the encrypted coordinates.The user judges whether the two users are in proximity according to the response from the server.Experimental result shows algorithm1runs fast and sends fewer messages,algorithm 2 is more secure,but it needs more computation and communication cost,and both users are required to be online.User can choose the more proper algorithm based on his trust in the server,the query performance,and the scenario.

location-based service;privacy preserving;security;encryption;proximity testing;location privacy

张一帆,尹树祥.用于保护位置隐私的邻近检测算法[J].计算机工程,2015,41(2):52-56.

英文引用格式:Zhang Yifan,Yin Shuxiang.Proximity Testing Algorithms for Preserving Location Privacy[J].Computer Engineering,2015,41(2):52-56.

1000-3428(2015)02-0052-05

:A

:TP311

10.3969/j.issn.1000-3428.2015.02.011

张一帆(1989-),男,硕士研究生,主研方向:云数据管理,隐私保护;尹树祥,硕士研究生。

2014-03-06

:2014-04-08E-mail:zhangyifan31@hotmail.com