基于概率推理的不确定性任务分配评价方法
2015-01-06贺毅辉潘明聪
贺毅辉,潘明聪,2,徐 伟,彭 辉
(1.解放军理工大学指挥信息系统学院,南京210007;2.南京陆军指挥学院作战实验中心,南京210045)
基于概率推理的不确定性任务分配评价方法
贺毅辉1,潘明聪1,2,徐 伟1,彭 辉1
(1.解放军理工大学指挥信息系统学院,南京210007;2.南京陆军指挥学院作战实验中心,南京210045)
作战任务的分解与分配是指挥决策中的重要过程,随着战场环境复杂度的增加,确定环境下的任务分配方法已不能适应作战需求。针对不确定性任务分配问题,分析作战任务分解、分配和执行过程中的多种不确定性因素,给出相应的形式化描述。在此基础上,提出一种基于概率推理的适应度计算方法,具体分析各种不确定性任务成功执行概率的计算过程,并给出算例进行验证。仿真结果表明,该方法能有效解决任务分配问题,并对任务分配方案进行定量评价。
不确定性;形式化描述;任务分配;概率推理;适应度
1 概述
作战任务的分解、分配与执行是作战指挥的重要过程,尤其是在战场信息化提高、环境复杂度增加以及参与作战的人员与设备多样化的现代战场情况下。这样的现状就要求指挥员能够对作战任务进行合理的分解、重组、排序和分配,以此确定何种执行体或人员在何时与何地开始何种任务,从而达到顺利完成作战任务的目的。目前,国内外针对任务分配问题提出了许多方法,文献[1]提出了一种分布式的任务分配方法,用于解决任务和成员动态变化时的任务分配问题,但没有考虑任务和智能体Agent发生变化时带来的不确定性问题;文献[2]用决策论方法来解决特殊环境中的任务分配问题,文中作者假定所有Agent具有相同的能力,且任务分配和执行过程中Agent能力不会发生变换;文献[3-4]提出了在动态环境下基于智能体能力的任务分配方法,虽然方法能够适应动态环境下的任务分配,但没有充分考虑任务分配过程中其他的不确定性。国内学者研究的任务分配方法,主要有如匈牙利算法[5]、层次分析法[6]、多属性决策方法[7]等,但这些方法均是在作战任务信息和执行人员信息充分的条件下进行的研究[8]。
在实际指挥决策中,任务分配过程往往存在多种不确定因素,传统的分配方法已经不能适应战场需求。鉴于此,本文利用与或树描述任务分解结构以及任务间的关系,分析任务分解、分配和执行过程中不确定性因素,并给出相应的形式化描述。在此基础上,提出一种基于概率推理的适应度(fitness)计算方法,具体分析各种不确定性任务成功执行概率的计算过程,并给出一个算例验证该方法的正确性。
2 问题分析与符号定义
在实际作战背景下,作战任务分配是一个动态变化前反馈的过程。图1表示作战任务分解、分配和执行的流程,从图中可以看出每个部分相互联系,而且战场态势的变化将导致作战任务的变更。因此,如何正确描述任务分解以及合理表示各种不确定性将影响作战指挥决策的效率。

图1 作战任务分解、分配与执行流程
2.1 基于与或树的任务分解描述
作战任务分解是任务组织形成的重要步骤之一,它通过将复杂任务转化为较简单的任务,一方面可以缓解单个执行体Agent完成任务的压力,便于任务的分配和执行;另一方面,当战场态势发生变化时,便于整个任务组织的调整。作战任务分解的实质是将任务变成一系列的可由Agent单独或协同完成的任务,并且包含了任务间的各种逻辑依赖关系。为体现作战任务分解的实质,本文采用“与或分解树”的表示方法。图2是任务的与或分解树表示。

图2 任务的与或分解树表示
在任务分解树中任务用节点表示,节点内为任务名称。任务间如果是顺序关系,则用虚线箭头连接节点,如图3(a)中,任务T4完成后才能执行任务T2。文中讨论的顺序关系仅限在同层次任务间;任务间如果是与关系,则在箭头线之间用圆弧连接,如图3(b)中,任务Ta与任务Tb的完成标志着任务T的完成;任务间如果是或关系,如图3(c)中,子任务T4或子任务T5的完成均标志着任务T的完成[9]。

图3 与或分解树中的任务关系
2.2 不确定因素分析与形式化描述
在实际的作战背景下,很多因素都将影响任务分配方案的形成,当作战任务和执行人员发生变化时,不确定性因素也将有所不同[10]。全面合理地分析任务分配过程中存在的不确定性因素,能够为任务分配方案的选取奠定基础。
(1)作战任务存在的不确定性
由于战场态势的千变万化将导致侦察到的情报信息可能存在误差,因此根据情报信息制定的作战任务同样存在不确定性,从而使得由作战任务分解得到的子任务具有不确定性。
定义1元任务指不可再分解、可由单个智能体Agent执行的任务,即任务分解树中叶子节点代表的任务,如图2中元任务T1,T2,…,T5。
元任务集合为:TM={T1,T2,…,Tm},其中,m为元任务的个数;智能体集合为:A={A1,A2,…,An},其中,n为智能体的个数。
定义2任务的存在概率,表示由总任务分解得到的子任务Ti是否存在的概率。本文用来处理任务存在的不确定性。
(2)作战任务执行的不确定性
由于在任务执行过程中存在许多未知与不可控的因素,例如,任务执行体Agent的执行能力影响任务能否成功被执行,而执行能力又受到战场环境等不确定因素的影响,因此任务的执行具有不确定性。
定义3任务成功被执行概率γTiAj,表示元任务Ti由智能体Aj执行成功的概率。考虑到不同任务分配给不同执行体时,任务成功被执行的概率有所不同。为方便讨论假设当任务分配方案确定后,该概率值即被确定。在本文中,γ′Ti和γTi分别表示元任务Ti初始成功被执行的概率和在考虑顺序关系对元任务Ti的影响后成功被执行的概率。
(3)子任务对父任务影响的不确定性
由任务分解树可以看出,任务的执行情况由其子任务决定。子任务成功被执行往往意味着父任务的完成。但是相反地,如果子任务未成功被执行却不意味着父任务一定不能完成,从而决定了子任务对父任务的影响具有不确定性。
定义4 与关系下子任务执行成功影响因子ωTi,表示若子任务间存在与关系,子任务Ti执行成功对父任务执行的影响,主要用来处理子任务的执行对父任务影响的不确定性。
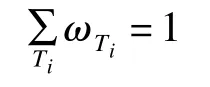
其中,Ti为具有同一父任务且相互之间为与关系的所有子任务。
(4)作战任务之间关系的不确定性
图2中显示任务之间存在多种关系,如顺序关系、与关系以及或关系等。其中,与、或关系的作用体现在子任务对父任务的影响,而顺序关系则使同一层次上不同任务之间存在作用与影响。本文主要讨论任务之间的影响,因此,与、或关系是确定的,也即顺序关系是不确定的。
定义5元任务顺序二元组<Ti,Tj>,表示在任务分解树中存在一条由叶节点Ti指向叶节点Tj的有向虚线边,即任务Tj须在任务Ti完成之后执行,如图2中存在顺序二元组<T4,T2>。所有的顺序二元组构成集合SEQ,其数学表达式如下:SEQ= {<Ti,Tj>|存在节点Ti指向Tj的虚线边}
定义6后序节点集合(Set of Later-Sequence, SLS),表示所有顺序二元组<Ti,Tj>中节点Tj的集合。

定义7 顺序关系存在的概率β<Ti,Tj>,本文考虑的顺序仅存于元任务之间,因此,β<Ti,Tj>表示元任务Ti与元任务Tj之间存在顺序关系的概率,本文主要用来处理任务间关系的不确定性。
(5)作战任务执行时间的不确定性
在作战任务分解、分配与执行过程中,通常会考虑关于任务执行时间的开始、结束和持续长短等因素。而不同任务对于执行时间有不同的约束,受到如执行体作战能力、任务规模以及作战环境等多种因素的影响,因此作战任务执行时间具有不确定性。本文将此类不确定性与任务执行的不确定性联合考虑,体现在任务被成功执行的概率上。
3 基于概率推理的适应度计算
在确定了任务分解树的结构、元任务序列以及不确定性概率值后,接下来需要根据智能体(Agent)执行能力表进行任务分配。已知元任务个数为m,智能体个数为n,假设智能体Agentj可以执行不同元任务,而元任务Ti能够同时分配给不同智能体,因此可能存在的分配方案数为nm。显然,随着n与m的增加,可选择的任务分配方案数指数级增加,因此任务分配问题为NP问题。而人工智能领域内智能搜索方法是解决NP问题的有效手段,而智能搜索算法中关键步骤是适应度的计算[11]。
3.1 不同关系下的概率推理
与或树中任务之间包含与、或以及顺序等关系,而任务之间的影响与作用也是通过这些关系进行传递的。如图3(a)中,任务T2和T3之间具有顺序关系,则可以认为任务T2是否被成功执行将影响任务T3的执行。因此在任务与或分解树中,同层次的任务之间存在相互作用。另外,子任务对父任务同样存在影响。由于相互作用与影响的任务可能存在多个,为不失一般性,本文将图3扩展成图4所示的情况,并给出不同关系下概率推理的过程。

图4 扩展后的与或分解树中任务关系
(1)顺序关系
如图4(a)所示,元任务Ti需在元任务Tj之后执行,因此元任务Tj的执行结果将影响元任务Ti的执行,则元任务Ti的成功被执行的概率γTi可以用式(1)表示。

对于元任务Tj而言,由于不存在指向节点Tj的虚线,则:
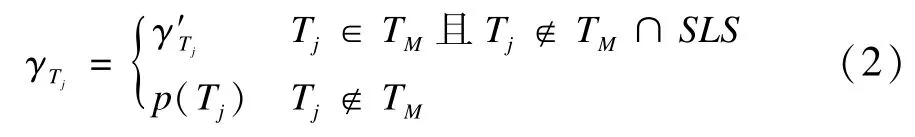
可以看出,式(2)是式(1)中β<Ti,Tj>=0的情况。
(2)与关系
如图4(b)所示,元任务Ti,Tl与Tj等之间两两存在与关系,即任务T完成的前提是元任务Ti,Tl与Tj等同时完成。以元任务Ti为例,考虑任务存在的不确定性、成功被执行的不确定性以及对父任务影响的不确定性,用p(T)Ti表示子任务Ti对父任务T的影响,见式(3)。由于子任务之间存在与关系,则任务T成功被执行的概率p(T)可用式(4)表示。

(3)或关系
如图4(c)所示,元任务Ti,Tl与Tj等之间两两存在或关系,即任务T完成的前提为元任务Ti,Tl与Tj中任意一个完成。以元任务Ti为例,用p(T)Ti表示子任务Ti的执行对父任务T的影响,具体见式(5)。由于子任务之间存在或关系,因此任务T成功被执行的概率p(T)可用式(6)表示。
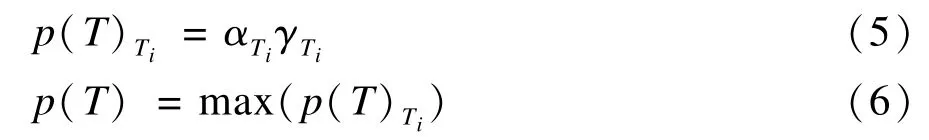
(4)与或关系
如图4(d)所示,元任务之间同时存在与关系以及或关系,本文首先将元任务之间为与关系的节点看作一个节点T′,利用式(3)和式(4)计算节点T′成功被执行概p(T′),然后再利用式(5)和式(6)计算节点T成功被执行概率p(T)。
3.2 适应度的计算步骤
根据之前的论述可知任务分配是一个NP问题,而解决NP问题的有效手段是采用智能搜索算法。在一般的智能搜索算法中都会涉及到适应度的计算,本文讨论的适应度也即总任务成功被执行的概率p(T)。具体的计算过程是在上节介绍概率推理的基础上,结合与或分解树结构进行概率传递。

步骤1初始化
确定与或分解树中叶子节点也即元任务集合TM,并为元任务存在概率αTi、初始成功执行概率γ′Ti、顺序二元组<Ti,Tj>存在的概率β<Ti,Tj>以及子任务Ti对父任务Ta的影响概率p(Ta|Ti)赋值。
步骤2更新概率值
由于元任务之间可能存在顺序关系,而顺序关系又能够影响元任务的成功被执行概率,因此需要对元任务的成功执行概率进行更新。如果元任务Ti∈TM∩SLS,则利用式(1)进行初始成功被执行概率的更新;如果元任务Ti∈TM且Ti∉TM∩SLS,则利用式(2)进行初始成功被执行概率的更新。
步骤3概率推理与传递
根据式(7)可知,本文中的适应度即根节点代表的总任务成功被执行的概率。因此,由叶节点出发,利用式(4)和式(6)进行概率推理得到根节点成功被执行的概率。具体推理与传递规则如下:如果节点之间仅存在与关系,利用式(4)向上进行推理;如果节点之间仅存在或关系,利用式(6)向上进行推理;如果节点之间既存在与关系又存在或关系,则根据3.1节的(4)中提出的规则向上进行推理。
经过以上3个步骤即可计算出总任务成功被执行的概率p(T),即适应度fitness。
4 仿真实验及结果分析
为验证本文提出方法的有效性,本文假设已经得到如图2所示的总任务T的分解树,则元任务集合TM={T1,T2,…,T5},SEQ={<T4,T2>},SLS= {T2}v。各概率初始值见表1。
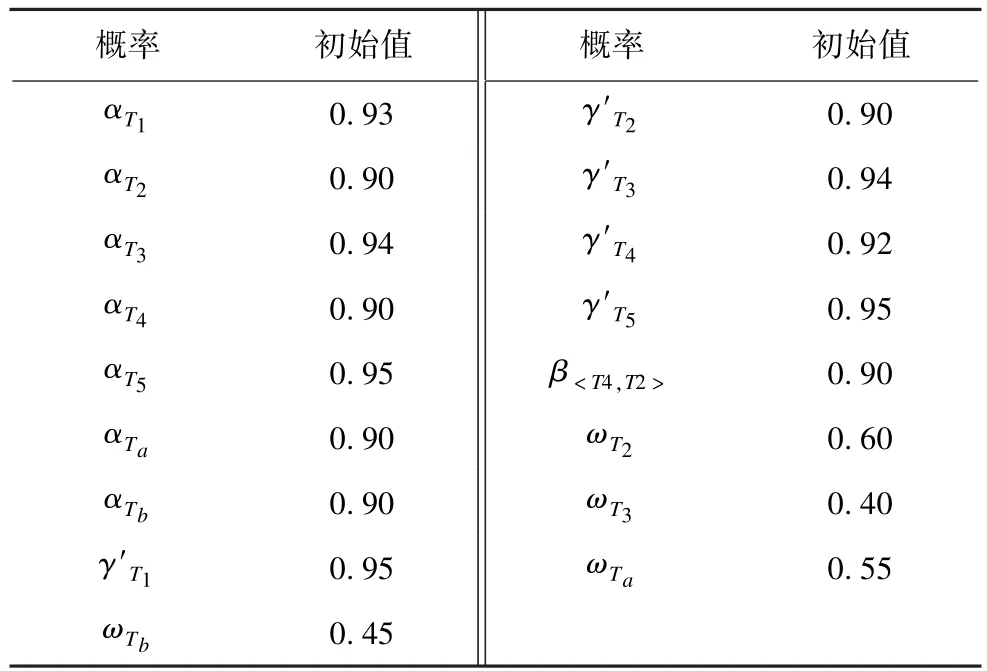
表1 概率初始值
通过3.2节步骤2可以计算出γT1=0.95,γT2= 0.83,γT3=0.94,γT4=0.92,γT5=0.95,从而根据步骤3可以计算出根节点成功被执行的概率p(T),即fitness=0.904。
由以上的计算过程可知,本文提出的适应度计算方法能够计算总任务的成功执行概率。为更好地体现本文提出的适应度计算方法能够有效地利用到遗传算法中,现将采用本文适应度计算过程的遗传算法与文献[12]中提出的基于能力的任务分配方法进行比较。文献[12]采用基于Agent能力的任务分配方法,主要目的是使Agent能力效能最大化,从而在最大程度上满足任务需求。
本文进行5组仿真对比实验,每组实验数据中Agent的能力值与各不确定性概率值不变,不同组实验数据间,需要改变不确定性概率值。每组均模拟计算100次,记录每次总任务的成功执行概率值,进行统计并计算总任务成功执行概率的平均值,统计结果如图5所示。

图5 仿真实验结果对比
从图5可以看出,5次实验中基于遗传算法计算的总任务成功执行概率的平均值比基于文献[12]提出的基于能力的方法计算值高,说明本文基于概率推理的适应度计算方法能够应用到遗传算法中,并能够有效解决作战任务分配问题。
5 结束语
为更好地实现作战任务的合理分配,本文从描述作战任务分解的方法出发,分析了在作战任务分解、分配和执行过程中存在的多种不确定性因素,并给出了各类不确定性因素的数学表达形式。作战任务分配问题是一个典型的NP问题,而智能搜索算法是解决NP问题的有效手段。因此,提出了一种基于概率推理的适应度计算方法,并给出了一个算例验证提出的方法。在算例的基础上,与其他任务分配方法进行仿真实验对比,结果表明,本文提出的方法能够有效地应对任务分解、分配和执行过程中的各类不确定性问题。下一步将重点研究如何处理任务分配过程中更多的不确定性因素。
[1] Macarthur K S,Stranders R,Ramchurn S D,et al.A DistributedAnytimeAlgorithmforDynamicTask Allocation in Multi-agent Systems[C]//Proceedings of the 25th AAAI Conference on Artificail Intelligence. San Francisco,USA:[s.n.],2011:85-90.
[2] Chapman A C,Micillo R A,Kota R,et al.Decentralized Dynamic Task Allocation:A Practical Game-theoretic Approach[C]//Proceedings of AAMAS’09.Budapest, Hungary:[s.n.],2009:16-20.
[3] Oliverra D,Ferreir A P R,Bazzaz A L C.A Swarm Based Approach for Task Allocation in Dynamic Agents Organizations[C]//ProceedingsofAAMAS’04. New York,USA:[s.n.],2004:1252-1253.
[4] Zhang Dandan,XieGuangming,YuJunzhi,etal. Adaptive Task Assignment for Multiple Mobile Robots via Swarm Intelligence Approach[J].Robotics and Autonomous Systems,2007,55(7):572-588.
[5] 朱德通.最优化模型与实验[M].上海:同济大学出版社,2003.
[6] 边馥萍,侯文华,梁冯珍.数学模型方法与算法[M].北京:高等教育出版社,2005.
[7] 徐泽水.不确定多属性决策方法及应用[M].北京:清华大学出版社,2004.
[8] 张 利,陈士明,张建军.不确定多因素下的多属性决策在任务分配中的应用[J].合肥工业大学学报:自然科学版,2008,31(6):851-853.
[9] 冯 磊.CGF协同行为建模关键技术研究[D].长沙:国防科学技术大学,2011.
[10] 张大川,张荣国,黄付亮,等.PSO算法在子任务分配中的应用[J].计算机工程,2011,37(24):183-186.
[11] 蔡益朝,张维明,刘 忠,等.基于遗传算法的实体分群问题的求解方法[J].计算机工程,2007,33(5): 4-6.
[12] 陶雪丽,郑延斌.基于能力及任务需求的多Agent任务分配方法[J].计算机应用与软件,2012,29(11): 181-184.
编辑 金胡考
Assessment Method of Uncertain Task Allocation Based on Probabilistic Reasoning
HE Yihui1,PAN Mingcong1,2,XU Wei1,PENG Hui1
(1.Command Information System College,PLA University of Science and Technology,Nanjing 210007,China; 2.Operations Research Center,Nanjing Army Command College,Nanjing 210045,China)
Decomposition and allocation of combat tasks play important roles in process of command and decision.With the increasing complexity of the battlefield environment,methods of task allocation under certain environment are no longer able to meet the needs of the commander.In order to solve this problem,this paper analyzes the uncertainty existing in the process of decomposition,allocation and execution of tasks,and gives the formal description of each uncertainty with mathematical method.On this basis,it proposes a method of calculating the fitness based on probabilistic reasoning.This method can be used in intelligent algorithm to assess the scheme of task allocation in quantity.Finally,the example verifies the reasonability and effectiveness of the proposed method.
uncertainty;formal description;task allocation;probabilistic reasoning;fitness
贺毅辉,潘明聪,徐 伟,等.基于概率推理的不确定性任务分配评价方法[J].计算机工程, 2015,41(2):31-35.
英文引用格式:He Yihui,Pan Mingcong,Xu Wei,et al.Assessment Method of Uncertain Task Allocation Based on Probabilistic Reasoning[J].Computer Engineering,2015,41(2):31-35.
1000-3428(2015)02-0031-05
:A
:TP391
10.3969/j.issn.1000-3428.2015.02.007
江苏省自然科学基金资助项目(BK2011120)。
贺毅辉(1973-),男,教授,主研方向:指挥信息系统,作战仿真;潘明聪、徐 伟,硕士;彭 辉,讲师、博士。
2014-01-21
:2014-04-25E-mail:xuwei_9002@163.com
