航空瞬变电磁正演中频时转换方法分析及系数的选取

杜兴忠，朱海东

（中国电建集团贵阳勘测设计研究院有限公司，贵阳 550081）

航空瞬变电磁正演中频时转换方法分析及系数的选取

杜兴忠，朱海东

（中国电建集团贵阳勘测设计研究院有限公司，贵阳 550081）

在瞬变电磁法正演计算中，常常需要频时转换来获得垂直磁场随时间的变化率。目前已经提出了多种频时转换方法，其中G－S变换法只涉及实数计算，具有较快的速度，因此已经成为航空瞬变电磁正演模拟的候选方法。由于航空瞬变电磁数据巨大，时间数较多，因此在保证精度的条件下怎样提高计算速度成为当前亟待解决的问题。鉴于大量频点的正弦变换和余弦变换具有较高的精度，这里使用三层和四层典型地电模型，通过比较余弦变换、正弦变换和不同点数G－S变换的正演计算结果来确定最佳的G－S变换系数。实验结果比较和分析认为，采用8个系数的G－S变换法不仅有较快的计算速度，而且也有较高的计算精度。

航空瞬变电磁法；G－S变换；正弦变换；余弦变换

0 引言

在瞬变电磁法中，常常需要通过频时转换来实现时间域的电磁响应计算。通常的频时转换法有G －S变换法［1－2］、余弦变换多项式近似法［3］、余弦变换法［4］、正弦变换法［4－5］、数值线性滤波法［6］、滞后褶积法［7］、延迟谱法［8］、混合算法［9－10］等。尽管在上述方法的基础上，许多研究者也提出了相应的改进方法，罗延钟［11］基于拉氏变换的延迟定理，建立了一种新的快速Gaver－Stehfest拉氏逆变换；阮百尧［12］提出了改进的Guptasarma算法并用于瞬变电磁的正演计算中；为了提高计算效率，蒋淑芬［13］等提出了一种基于复积分的正余弦变换算法；徐振平等［14］给出了改进的余弦变换方法，但是都未能在计算效率上有显著改善。昌彦君［15］等通过比较余弦变换多项式近似法、G－S变换法和Guptasarma滤波算法，认为Guptasarma滤波算法计算速度快，但是晚期误差范围大，适用的时间范围最小；余弦变换法精度高，适用的时间范围最宽，但是耗时最多；G －S变换法的计算精度和耗时介于两者之间［15］。此外，孙业发［5］等通过比较正弦变换、余弦变换和余弦变换的折线逼近法，最后认为正弦变换在瞬变电磁响应晚期的转换精度明显高于其他两种方法。

由于航空瞬变电磁法数据庞大，涉及该方法的正演计算耗时较大，为此作者以大量频点（300个）的正弦变换法和余弦变换法为基准，通过与不同系数的G－S变换法的正演计算结果进行比较，确定出G－S变换法的最佳系数，以保证航空瞬变电磁正演计算在拥有较高计算精度的条件下，具有较高的计算速度。

1 航空瞬变电磁法正演计算

航空瞬变电磁法是以飞机为运载工具，发射脉冲电流，在发射机关断电流时，观测二次磁场随时间的衰减特性，进而推断地下不同介质的分布，从而解决各类地质问题的方法［16］。

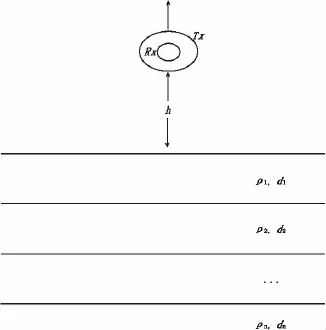
图1 航空瞬变电磁正演模型Fig.1 The forward model of airborne transient electromagnetic

对于图1所示的航空瞬变电磁正演模型，中心回线装置的航空瞬变电磁响应计算公式表示为［17］式（1）：

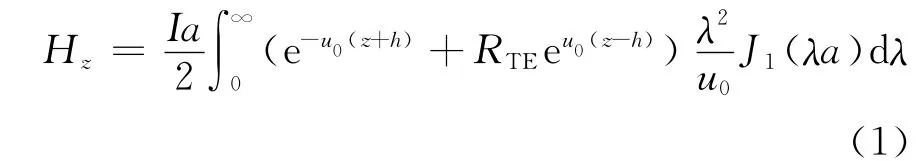
其中：J1表示一阶第一类贝塞尔函数；a表示发射线圈半径；λ是积分变量；RTE表示反射系数，具体为：

并且

式中：ω是角频率；kn是第n层的波数；σn是第n层的电导率；通常取大地的导磁率μn和自由空间的导磁率μ0相等，在准静态情况下，通常取u0＝λ。

根据上述公式可以实现航空瞬变电磁法一维正演模拟，其计算步骤如下：

1）设置系统参数和地电模型参数。

2）计算反射系数。

3）汉克尔变换计算。

4）频时转换计算。

5）计算电磁响应。

在上述计算步骤，影响电磁响应精度和计算效率的关键是汉克尔变换和频时转换。

汉克尔变换数值滤波计算方法有很多，这里采用Guptasarma和Singh［18］所提出的数字滤波方法。

汉克尔积分变换的一般形式可以表示为式（6）：

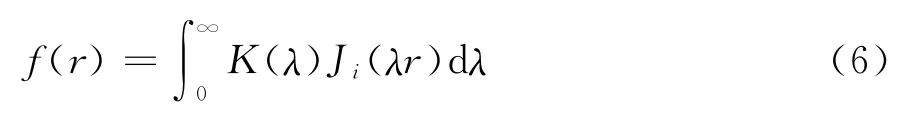
其中：K（λ）表示待变换的函数；Ji表示i阶第一类贝塞尔函数；r是一个已给出的定值；λ表示被积函数。数字滤波器有一组滤波系数Wi和两个常数（位移a和采样间隔s）。位移a决定了输入函数采样的起始点，间隔s决定抽样时的时间间隔。文献［18］给出了汉克尔变换的计算公式：

一般常用的汉克尔变换滤波系数有安德森［19］引入的283个系数和801个系数，尽管其精度较高，但是计算速度较慢，所以这里主要采用文献［18］中给出的滤波系数，即零阶有61或120个系数，一阶有47或120个系数。

2 频时转换

2.1 正弦、余弦变换

根据航空瞬变电磁响应计算公式（1）可以求得Hz。令激发波为阶跃波：

对式（8）进行傅氏变换，可得式（9）。

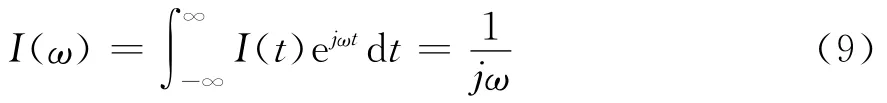
将式（8）代入式（9）再经过傅氏反变换，得到式（10）与式（11）。

根据正余弦变换数值滤波算法［4］，式（10）和式（11）可以分别化为：

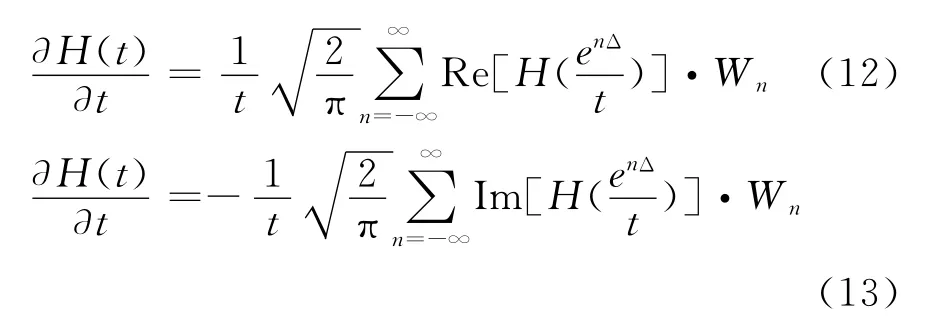
2.2 G－S变换

Gaver－Stehfest逆拉氏变换（简称G－S变换）是纯实数运算，只需对较少的拉氏变换量s值做计算，因而计算速度较快。根据文献［1］，可以获得用G－S变换作逆拉氏变换的算法为：对给定的时间t，时间域的响应值f（t），由拉氏变换域中的变量（其中m＝1，2，…，n）的拉氏域响应值F（sm）算出：

表1 G－S变换系数Tab.1 G－S transformation coefficients

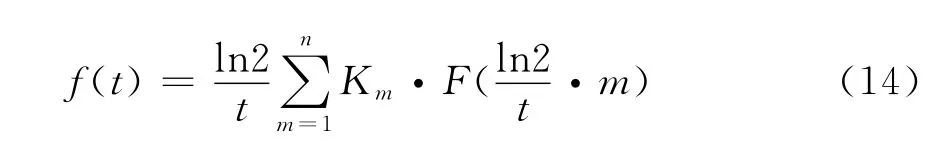
式中：n是决定于计算机位数的正偶整数；Km是G －S变换系数，且可由公式（15）计算得出。

式中：m＝1，2，…，n；求和下限i1是的整数部分。

在航空瞬变电磁响应计算中，为了在保证计算精度的条件下获得较高的计算效率，作者考查滤波系数个数分别取n＝6、8、10、12、14、16时所对应的响应值。根据式（15）求得不同滤波系数个数所对应的G－S变换系数（表1）。

对于G－S变换系数个数n的取值问题，目前存在多种不同的观点，Wooden［20］等认为n取8或者10比较合适，当n取得更大时，会使得变换变得不稳定，数据结果会发生振荡；罗延钟［21］等认为n取16合适；昌彦君和张桂青等［15］则认为n取12合适。作者结合航空瞬变电磁数据特性，通过正演模拟计算确定G－S变换系数个数n的取值，同时和使用正、余弦变换的响应计算结果进行对比分析，验证n的取值的正确性。

3 电磁响应计算结果及分析

3.1 G－S变换系数对应的电磁响应对比实验

为了比较不同数量的G－S变换系数对应的电磁响应，设置系统参数如下：发射电流为阶跃电流，其归一化值为1A，发射线圈半径为1m；接收线圈有效面积归一化为1m2；飞行高度为30m。设置三层K型地电模型的参数为：第一层电阻率为10Ω· m，层厚为50m，第二层电阻率为100Ω·m，层厚为50m，第三层的电阻率为50Ω·m。在上述系统参数和地电模型的参数设置下，使用表1中不同的G－S变换系数，通过正演计算，获得的电磁响应如图2所示。

从图2中可以看出，不同系数的G－S变换所对应的电磁响应差异主要在晚期，说明G－S变换系数对航空瞬变电磁阶跃响应的晚期影响较大，而早期响应几乎不受影响。此外，6点G－S变换和16点G－S变换的电磁响应在晚期发生振荡，可以认为6点G－S变换和16点G－S变换不适用于航空瞬变电磁响应计算，实际上，我们在实验中也发现，小于6点或大于16点的G－S变换系数在电磁响应晚期都发生振荡，因此对于航空瞬变电磁正演模拟，只余8点、10点、12点和14点G－S变换可以考虑作为候选频时转换方法。同时从图2中也发现，10点、12点、14点G－S变换的阶跃响应值几乎一致，而8点G－S变换的阶跃响应值和这3种G －S变换在晚期存在一定差异。

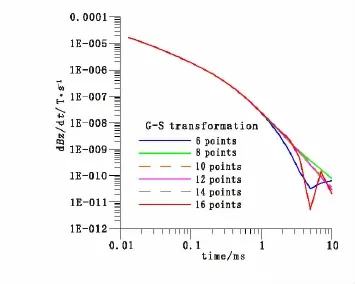
图2 不同系数个数的G－S变换所对应的阶跃响应Fig.2 The step response values corresponding to the G－S transform of different coefficients

对于航空瞬变电磁响应计算，我们在8点、10点、12点和14点G－S变换进行选择，分别将8点、10点、12点、14点G－S变换和余弦变换的K型地电模型阶跃响应值进行对比（图3）。从图3中可以看出，在早期，8～14点G－S变换和余弦变换所分别对应的航空瞬变电磁响应的形态和趋势基本一致，只是幅值上稍有差异；但是在晚期，10～14点G －S变换和余弦变换所对应的电磁响应则有很大差异，而8点G－S变换和余弦变换的电磁响应比较接近，而当频点足够多时，余弦变换的晚期响应值更准确和稳定并且具有更宽的时间范围［15］，这里假设8点G－S变换更能适用于航空瞬变电磁法。

3.2 G－S变换和余弦变换实验对比

为了验证8点G－S变换选取的正确性和适用性，这里考虑三层地电模型A型、H型、Q型和四层地电模型AA型、AK型、KH型、KQ型、QQ型、QH型、HA型和HK型，并对比8点G－S变换、10点G－S变换和余弦变换得到的阶跃响应值。系统参数的设置同上，地电模型的设置为：A型地电模型的电阻率从上到下依次为1 0Ω·m、5 0Ω·m、1 0 0 Ω·m；H型地电模型的电阻率从上到下依次为50 Ω·m、10Ω·m、100Ω·m；K型地电模型的电阻率从上到下依次为10Ω·m、100Ω·m、50Ω·m；Q型地电模型的电阻率从上到下依次为100 Ω·m、50Ω·m、10Ω·m；AA型地电模型的电阻率从上到下依次为10Ω·m、50Ω·m、100Ω·m、200Ω·m；AK型地电模型的电阻率从上到下依次为10Ω·m、50Ω·m、100Ω·m、50Ω·m；KH型地电模型的电阻率从上到下依次为10Ω·m、50 Ω·m、10Ω·m、50Ω·m；KQ型地电模型的电阻率从上到下依次为10Ω·m、100Ω·m、50Ω·m、10Ω·m；QQ型地电模型的电阻率从上到下依次为200Ω·m、100Ω·m、50Ω·m、10Ω·m；QH型地电模型的电阻率从上到下依次为100Ω·m、50Ω·m、10Ω·m、50Ω·m；HA型地电模型的电阻率从上到下依次为50Ω·m、10Ω·m、50 Ω·m、100Ω·m；HK型地电模型的电阻率从上到下依次为50Ω·m、10Ω·m、50Ω·m、10Ω·m。每种地电模型各层之间的层厚都为50m。在典型的三层地电模型和四层地电模型中所获得的电磁响应值分别如图4和图5所示。

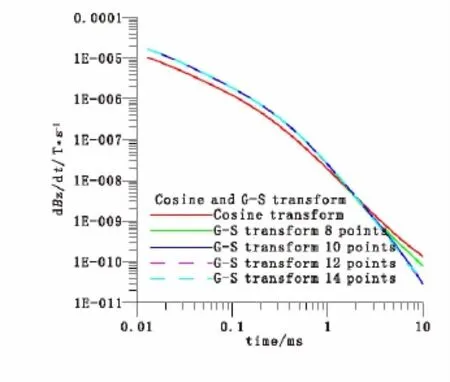
图3 K型地电模型中G－S变换和余弦变换的阶跃响应值Fig.3 The step response values of G－S transform and cosine transform in K Geoelectric model

图4 8、10点G－S变换和余弦变换在三层地电模型中的阶跃响应值Fig.4 The step response values of 8，10points G－S transform and cosine transform in three－layer model

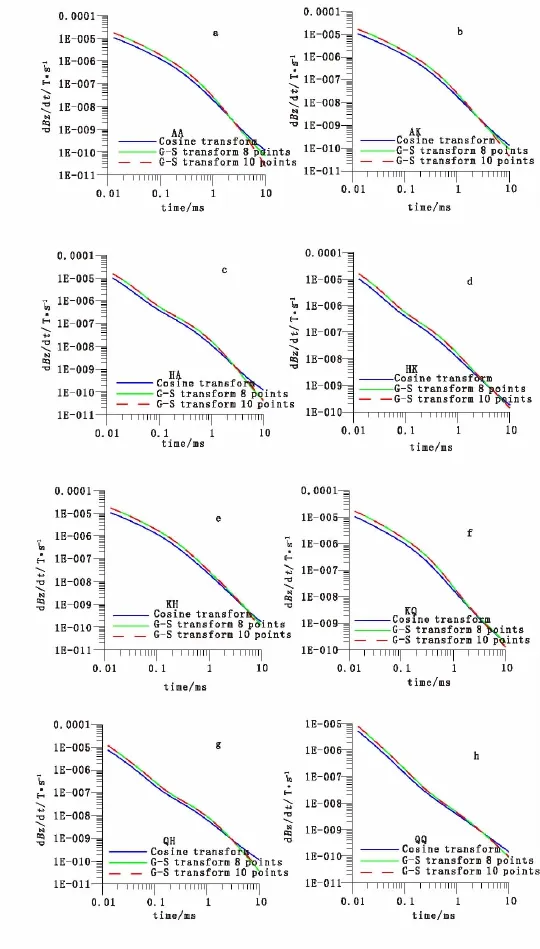
图5 8、10点G－S变换和余弦变换在四层地电模型中的阶跃响应值Fig.5 The step response values of 8，10points G－S transform and cosine transform in four－layer model

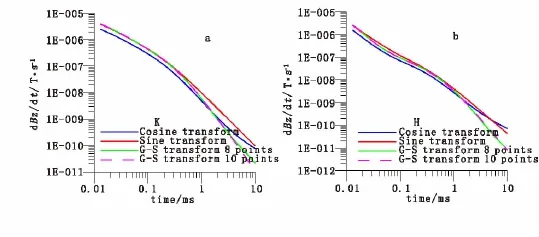
图6 8、10点G－S变换与余弦变换和正弦变换在K型和H型上的阶跃响应Fig.6 The step response values of 8，10points G－S transform，cosine transform and sine transform in K－type and H－type geoelectric model respectively （a）K型；（b）H型

在图4和图5中，蓝色实线为余弦变换得到的阶跃响应曲线，绿色实线为8点G－S变换得到的阶跃响应曲线，红色虚线为10点G－S变换得到的阶跃响应曲线。从A型、K型、AA型、AK型地电模型图中可以看出，在晚期的时候绿色实线较红色虚线明显更靠近蓝色实线，而在其他几种地电模型图中绿色实线和红色虚线几乎重合，这说明8点和10点G－S变换在一些模型中，其阶跃响应基本一致；而在另一些模型中，8点G－S变换所得到的阶跃响应在晚期更接近于余弦变换所得到的阶跃响应，这就证明了8点G－S变换适用于航空瞬变电磁法，因为其不仅拥有较高的计算精度，同时能获得更快的计算速度。

3.3 G－S变换、余弦和正弦变换实验对比

孙业发［5］等认为正弦变换在瞬变电磁响应晚期的转换精度明显高于余弦变换和余弦变换的折线逼近法。为了考查8点G－S变换的转换精度，这里以三层K型和H型地电模型为例，对8点G－S变换、10点G－S变换、余弦变换和正弦变换的电磁响应进行比较。在地电模型的参数设置中，K型模型的电阻率由上至下分别为：10Ω·m、100Ω·m、50 Ω·m，H型模型的电阻率由上至下分别为：100 Ω·m、10Ω·m、100Ω·m，两种地点模型各层之间的层厚均为50m。在K型和H型地电模型上，8 点G－S变换、10点G－S变换、余弦变换和正弦变换的电磁响应如图6所示。

从图6中可以看出，正弦变换得到的响应结果和余弦变换、G－S变换得到的响应结果在早期走势基本一致，而在晚期它们之间存在一定差异。可以看到在晚期的时候8点G－S变换（绿色实线）比10点G－S变换（粉红色虚线）更靠近正弦变换（红色实线）或者余弦变换（蓝色实线），验证了8点GS变换具有较高的计算精度。

从运算时间上来说，在同等计算机平台上（CPU：i3，内存：3G；操作系统：Windows 7；语言：Matlab 2010b），G－S变换耗时为0.063s，而正弦变换和余弦变换耗时分别为4.768s和4.766s。这说明正、余弦变换尽管有较宽的时间范围，但是其计算量太大，而G－S变换具有较高的计算效率，这是由于G－S变换系数较少，且不涉及复数运算，而正、余弦变换需要进行复数计算。

综合上述的计算精度和计算时间分析，可以看到，在计算量较大的航空瞬变电磁法中，8点G－S变换比较适用，因为其不仅具有较高的计算精度，而且还有很高的计算效率。

4 结论

在典型的三层和四层地电模型中，对8点、10点、12点、14点、16点G－S变换以及正弦变换和余弦变换的阶跃响应进行对比分析，获得了如下结论：

1）当需求较高的转换精度时，正弦变换和余弦变换所需的频点数较多，因此导致计算量增大，是G －S变换耗时的几十倍。

2）在不同点数的G－S变换中，8点G－S变换具有较高的转换精度，仅次于高频点的正弦变换和余弦变换。

3）在计算效率上，和其他的G－S变换以及正、余弦变换相比，8点G－S变换具有最高的计算效率。

4）由于8点G－S变换在正演计算中不仅具有较快的计算速度，而且也具有较高的计算精度，所以在数据量巨大的航空瞬变电磁正演计算中，应该选择其作为频时转换方案。

［1］ KNIGHT J H，RAICHE A P.Transient electromagnetic calculations using the Gaver－Stehfest inverse Laplace transform method［J］.GEOPHYSICS，1982，47（1）：47－50.

［2］ 朴华荣.电磁测深法原理［M］.北京：地质出版社，1990.

PIAO H R.Principle of electromagnetic sounding method［M］.Beijing：Geological Publishing，1990.（In Chinese）

［3］ 考夫曼A A，凯勒G V.频率域和时间域电磁测深［M］.地质出版社，1987.

KAUFMAN A A，KELLER G V.Frequency and transient soundings［M］.Geology Press，1987.（In Chinese）

［4］ 王华军.正余弦变换的数值滤波算法［J］.工程地球物理学报，2004，1（4）：329－335.

WANG HJ.Digital filter algorithm of the sine and cosine transform［J］.Chinese Journal of Engineering Geophysics，2004，1（4）：329－335.（In Chinese）

［5］ 孙业发，李桐林，范翠松，等.中心回线瞬变电磁响应计算的频－时域转换方法研究［J］.地球物理学进展，2014，29（3）：1243－1247.

SUN Y F，LI T L，FAN C S，et，al.Research on frequency－time domain transform method in centralloop transient electromagnetic field response computation［J］.Progress in Geophysics，2014，29（3）：1243 －1247.（In Chinese）

［6］ GUPTASARMA D.Computation of the time－domain response of a polarizable ground［J］.GEOPHYSICS，1982，47（11）：1574－1576.

［7］ ANDERSON W L.Fast Hankel transforms using related and lagged convolutions［J］.ACM TRANS.ON MATH.SOFTWARE，1982（8）：344－368.

［8］ NEWMAN G A，HOHMANN G W，ADNERSON W L.Transient electromagnetic response of a three－dimensional body in a layered earth［J］.GEOPHYSICS，1986，51（8）：1608－1626.

［9］ GOLDMAN M M.The integral－finite－difference method for calculating transient electromagnetic fields in a horizontally stratified medium［J］.GEOPHYSICAL PROSPECTING，1983，31：664－686.

［10］李汝传，王书民，孙鸿雁.用混合算法计算电偶源瞬变电磁响应［J］.物探与化探，2002，26（3）：215－217.

LI R CH，WANG SH M，SUN H Y.The application of mixed algorithm to the Calculation of transient electromagnetic response of couple source.Geophysical ＆Geochemical Exploration，2002，26（3）：215－217.（In Chinese）

［11］罗延钟，昌彦君.G－S变换的快速算法［J］.地球物理学报，2000，43（5）：684－690.

LUO Y ZH，CHANG Y J.A rapid algorithm for GS transform.Ch inese Journal of Geophysics，2000，43 （5）：684－690.（In Chinese）

［12］阮百尧.Guptasarma算法在瞬变电磁正演计算中的应用［J］.桂林工学院学报，1996，16（2）：167－170.RUAN BY.Applied of Guptasarma algorithm in TEM ＇s forward［J］.Journal of Guilin Institute of Technology，1996，16（2）：167－170.（In Chinese）

［13］蒋淑芬，向淑晃.一种正余弦变换的高效算法［J］.工程地球物理学报，2007，4（5）：512－515.

JIANG SH F，XIANG SH H.An Eifficient Method of Calculating the Sine and Cosine Transform.Chinese Journal of Engineering Geophysics，2007，4（5）：512 －515.（In Chinese）

［14］徐振平，胡文宝.基于快速余弦变换的低频电磁场数值滤波法正演［J］.石油天然气学报（江汉石油学院学报），2011，33（1）：63－67.

XU ZH P，HU W B.Low frequency electromagnetic field numerical filtering method based on fast cosine transform［J］.Journal of Oil and Gas Technology，2011，33（1）：63－67.（In Chinese）

［15］昌彦君，张桂青.电磁场从频率域转换到时间域的几种算法比较［J］.物探化探计算技术，1995，17（3）：25 －29.

CHANG Y J，ZHANG G Q.Comparison among three transformation algorithms of electromagnetic field from frequency domain to time domain.Computing Techniques for Geophysical and Geochemical Exploration，1995，17（3）：25－29.（In Chinese）

［16］NABIGHIAN M N.Electromagnetic Methods in Applied Geophysics：Volume 2，Application，Parts A and B［M］.Tulsa：Society of Exploration Geophysics，1991.

［17］NABIGHIAN M N.Electromagnetic Methods in Applied Geophysics：Volume 1，Theory［M］.Tulsa：Society of Exploration Geophysics.1988.

［18］GUPTASARMA D，SINGH B.New digital linear filter for Hankel J0and J1transforms［J］.GEOPHYSICAL PROSPECTING，1997，45（5）：745－762.

［19］ANDERSON W L.Improved digital filters for evaluating Fourier and Hankel transform integrals［R］.U.S.G.S.REPORT，GD－75－012，PAGES，223，1975.

［20］WOODEN B，AZARI M，SOLIMAN M.Well test analysis benefits from new method of Laplace space inversion［J］.OIL ＆GAS JOURNAL，1992，90（29）：108－110.

［21］罗延钟，张胜业，王卫平.时间域航空电磁一维正演研究［J］.地球物理学报，2003，46（5）：719－724.

LUO Y ZH，ZHANG SH Y，WANG W P.A research on one－dimension forward for aerial electromagnetic method in time domain［J］.Chinese Journal of Geophysics，2003，46（5）：719－724.（In Chinese）

Analysis and coefficients selection of frequency－time conversion methods for airborne transient electromagnetic forward modeling

DU Xing－zhong，ZHU Hai－dong
（Guiyang Hydropower investigation design and Research Institute，CHECC，Guiyang 550081，China）

The change rates of vertical magnetic field with time are usually obtained by the frequency－time conversion method in transient electromagnetic modeling.At present，despite many kinds of frequency－time conversion methods have been proposed，the G－S transform with faster computation speed has become an important candidate for airborne transient electromagnetic method.Due to the huge data and the long time of airborne electromagnetic method，how to improve the computation speed of modeling under the certain accuracy becomes a key problem to be solved.Due to the higher frequency－time conversion precision of sine and cosine transform with the larger number of frequency coefficients，this paper may determine the best coefficients of G－S transform by the comparison of the forward modeling results of sine transform，cosine transform and G－S transform with different frequency based on the three－layer and four－layer model.By comparison and analysis of the experimental results，this paper shows that the G－S transform with 8coefficients not only has faster speed，but also a high degree of accuracy.

airborne transient electromagnetic；G－S transform；sine transform；cosine transform

P 631.3

A

10.3969／j.issn.1001－1749.2015.06.01

1001－1749（2015）06－0671－09

2015－08－30改回日期：2015－09－25

贵州省科学技术基金（［2013］2297）

杜兴忠（1973－），男，博士，高级工程师，主要从事工程物探技术研究和应用，E－mail：xingzhongdu＠163.com。