利用阻尼型高斯牛顿法的激发极化数据聚焦反演

叶益信，李泽林，付 宸，丁尚见

（1.东华理工大学 放射性地质与勘探技术国防重点学科实验室，南昌 330013；2.中国地质大学 地球内部多尺度成像湖北省重点实验室，武汉 430074）

利用阻尼型高斯牛顿法的激发极化数据聚焦反演

叶益信1，2，李泽林1，付 宸1，丁尚见1

（1.东华理工大学 放射性地质与勘探技术国防重点学科实验室，南昌 330013；2.中国地质大学 地球内部多尺度成像湖北省重点实验室，武汉 430074）

利用阻尼型高斯牛顿法求解反演目标函数，并将粗糙度矩阵约束和最小支撑泛函约束以及参考模型和模型参数界限约束引入到目标函数中，同时结合预条件共轭梯度法进行反演迭代，实现了激发极化数据三维聚焦反演快速计算。通过对几个典型模型的试算，并与传统光滑模型约束的反演结果进行比较，表明该反演算法的可靠性和稳定性较好，并且算法速度快，占用内存低且易于并行化。

激发极化；高斯牛顿法；聚焦反演；最小支撑泛函

0 引言

激发极化（IP）法的应用范围非常广泛，无论是在金属矿和非金属矿产勘查［1－2］，还是在寻找地下水资源和地热田方面［3－4］，都获得了成功地应用，近年来又拓展到环境监测领域［5－6］。国内、外有关学者对激发极化法正反演也有较多的研究，Pelton等［7］利用参考数据库中数据插值计算偏导数，实现了激发极化二维最小二乘反演方法；日本的Sasaki博士［8］在前人的基础上发展了有限元电阻率／极化率数据的二维最小二乘反演方法；Ellis等［9］也将解的先验信息加入目标函数中，使反演结果更符合实际；Oldenburg等［10］在电阻率反演的基础上，讨论了几种激发极化反演方法；Li等［11］研究了激发极化数据的三维反演；阮百尧等［12］在前人研究的基础上，实现了电阻率和极化率分块连续变化的激发极化数据二维最小二乘反演算法，并编制了相应的程序，在各种金属矿和非金属矿勘探的数据处理中起了非常大的作用；吴小平［13］利用共轭梯度法实现了激发极化数据的三维快速反演，大大提高了反演速度；黄俊革［14］利用异常电位法实现了电阻率和激发极化法三维有限元正反演，提高了正演和反演精度；陈进超等［15］应用非结构化三角网格剖分实现了激发极化法2.5维有限元正演，模拟具有较高的计算精度和较快的计算速度；蒋首进［16］研究了激发极化法二维最小二乘反演方法并将其应用到矿产勘查中，取得了较好的应用效果。

尽管对激发极化数据的正反演研究较多，但还需从不同侧面进行研究，以期提高激发极化法的应用效果。这里对如何提高激发极化数据反演分辨率问题，给出了具体解决方案。粗糙度约束有效排除了不真实的多余结构，引入最小支撑泛函约束［17］即聚焦突出异常体边界，异常体范围小，反演结果更趋于真值。同时利用阻尼型高斯牛顿法求解反演目标函数，并且采用共轭梯度法进行反演迭代，实现了激发极化数据三维快速反演计算，解决了内存占用量巨大的问题，且易于并行化。通过对典型模型的反演试算，表明了该反演算法的可靠性和稳定性较好。

1 反演理论

首先给出一个基本的正则化反演目标函数：

其中：Wd、Wm分别表示数据和模型的权系数矩阵；dobs为观测数据；d（m）为正演理论值；m为模型参数；mref为参考模型；α是正则化因子。

在本算法中，Wd采用式（2）的对角矩阵：

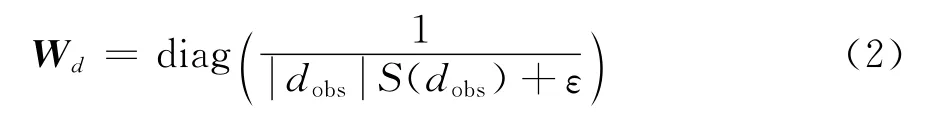
式中：S（dobs）为观测数据的标准偏差；ε为权重项，避免在很小的数据上权重过大。

为了减小多解性，使反演结果更加真实，光滑反演通常采用一阶正则化或二阶正则化粗糙度矩阵作为模型的权系数矩阵，一阶正则化粗糙度矩阵为式（3）：

式中：Rx、Ry和Rz分别为x、y和z方向的梯度。

虽然采用一阶正则化粗糙度约束能使反演结果呈现良好的平缓结构，有效排除不真实的多余突变结构，但地质体之间通常存在明显的分界面，不是平缓过渡的。因此光滑反演结果通常过于平缓，故不利于地质解释。根据聚焦反演原理［17］，引入最小支撑泛函作为模型约束条件（式（4））。

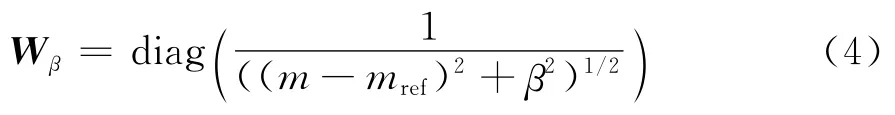
其中β为不等于“0”的小数，根据最小支撑泛函的性质，在反演过程中，模型参数中异常体剖面的面积会尽可能聚焦到最小，从而可以提高模型结构的分辨率。然后将模型参数转化为加权模型空间形式，令，由此新的反演目标函数可改写为式（5）：

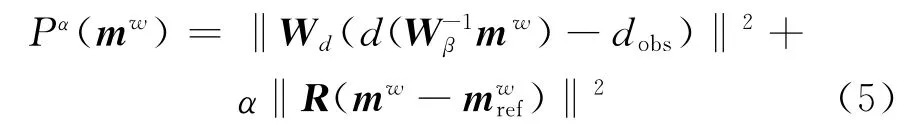
有了目标函数（式（5））后，用高斯牛顿法选择合适的正则化参数来反演出符合观测数据的模型，首先定义一个初始模型mwi，通常采用最接近真实模型的均匀半空间，然后对式（5）线性化后得到式（6）。

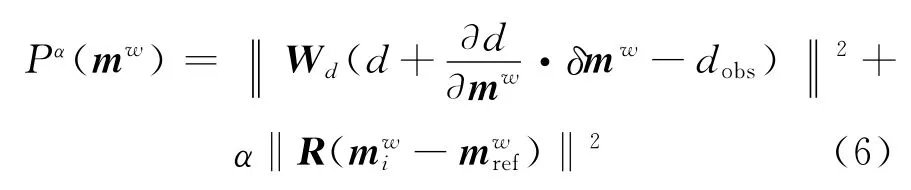
为了得到式（6）的最小值，将式（6）对mw求导，并使其等于零，得到高斯牛顿更新公式为式（7）。

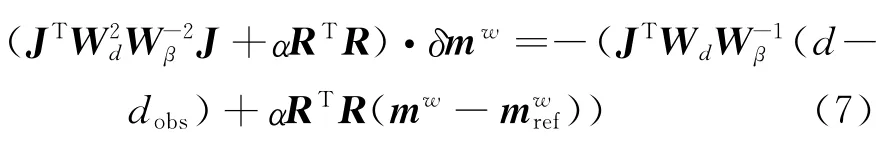
求解式（7）可得到模型的修正量δmw，由此可得到一个新的模型（式（8））。

式中：α是线性搜索参数，这里采用Armijo步长准则对α线性搜索，确保目标函数能够充分减小。

迭代后，未加权的模型参数可由式（9）求得。

重复上述步骤，直到目标函数减小到一定值或模型修正量小于一定值。

同时为了缩小解的范围，减少解的非唯一性，提高反演分辨率，对模型参数施加界限约束，假设在反演中地形介质电性变化的上边界η＋（r）和下边界η－（r），这样，在每次迭代过程中可将参数的变化量控制在界限范围内，而且也不会出现负的极化率值，算法可写为式（10）。

这样参数范围被限定在：［η－（r），η＋（r）］，背景均匀参数和最大异常参数可由先验信息获得。

2 模型反演试验

反演中的观测数据为E－SCAN方式测量的双极－双极电位值φobs。由于它们的变化范围很大，一般用对数来标定观测数据及模型参数，即dobs＝lnφobs及m＝lnσ。视极化率数据可依据Seigel［18］理论得到，可表示为式（11）。

写成矩阵形式为式（12）。

其中J为电阻率反演中的偏导数矩阵的负矩阵。由于J已在电阻率反演中得到，因此在电阻率三维反演基础上，只需少量计算即可获得激发极化数据的反演结果。电极系布置如图1所示，共4 332个数据。

图1 地表电极排列布置示意图Fig.1 The configuration of the electrodes array on the earth surface

2.1 单个异常体模型

模型一为一个大小为20m×20m×17m、电阻率为200Ω·m、极化率为1%的均匀半空间含有一个大小为2.5m×2.5m×4m、电阻率为10Ω·m、极化率为10%的异常体，其顶部埋深为2m，其z＝4m处的水平切片（XOY平面）如图2（a）所示，y＝0 m处的垂直切片（XOZ平面）如图2（b）所示。模型网格剖分成40×40×20共32 000个单元。

反演初始模型为电阻率200Ω·m、极化率1%的均匀半空间，所有计算均在双核2.9GHz CPU 和8GRAM个人计算机上完成。共迭代10次，共耗时13.5min。电阻率和极化率反演结果分别如图3和图4所示，并与光滑模型约束的反演结果进行了比较，黑线框表示模型的边界位置。对比两种模式的反演结果可看出，光滑模型约束的反演结果在异常体位置出现了低阻高极化异常值，但低阻异常值约80Ω·m左右，极化率异常值为7%左右，基本能够表征异常体的存在，但是异常范围偏大，尤其是电阻率的反演结果，与异常体真实电阻率值相差较大，而聚焦反演结果电阻率极化率异常更明显，电阻率异常最小值接近10Ω·m，极化率异常最大幅值接近10%，与真实异常体特征更接近，改善了异常体的聚焦效果，对异常体的定位更准确。

图5为两种反演方法的归一化迭代拟合差随迭代次数的变化情况，从图5中可看出，两种反演算法都能稳定收敛，但是聚焦反演的拟合差更小，收敛速度较快。

2.2 两个异常体模型

模型二为一个大小为20m×20m×17m、电阻率为200Ω·m、极化率为1%的均匀半空间含有两个大小为2.5m×2.5m×4m、电阻率为10 Ω·m、极化率为10%的异常体，其顶部埋深为2m，其z＝4m处的水平切片（XOY平面）如图6（a）所示，y＝0m处的垂直切片（XOZ平面）如图6（b）所示。网格剖分与模型一相同。

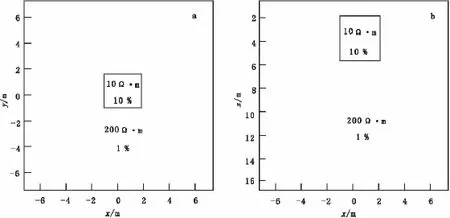
图2 模型一切片图Fig.2 A depth slice of the model 1

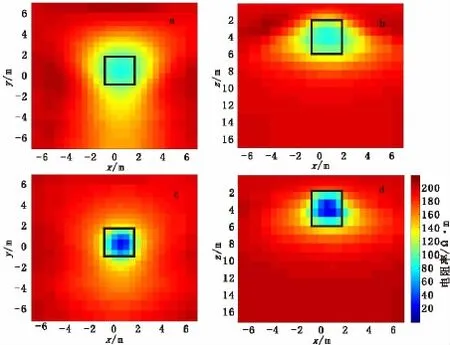
图3 模型一电阻率光滑反演与聚焦反演结果比较Fig.3 Comparisons of focusing inversion with smoothing inversion for model 1

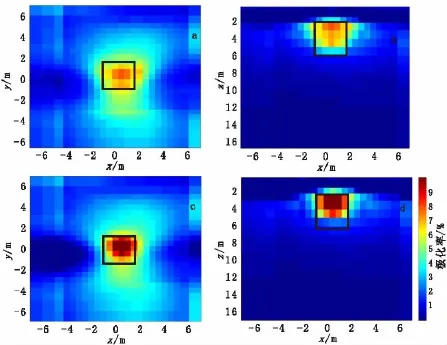
图4 模型一极化率光滑反演与聚焦反演结果比较Fig.4 Comparisons of focusing inversion with smoothing inversion for model 1

反演初始模型为电阻率200Ω·m、极化率1%的均匀半空间，反演共迭代10次，共耗时13.6 min。图7和图8分别为电阻率和极化率的反演结果，并与光滑模型约束的反演结果进行了比较，黑线框表示模型的边界位置。对比两种模式的反演结果可看出，光滑模型约束的反演结果在异常体位置出现了低阻高极化异常，低阻异常值约90Ω·m左右，极化率异常值为6%左右，基本能够表征异常体的存在，但是整体聚焦效果较差，图像较模糊，尤其是电阻率反演结果，两个异常体的电阻率值与真实值相差较大，而聚焦反演结果低阻高极化异常更明显，电阻率异常最小值接近20Ω·m，极化率异常最大值接近10%，与真实异常体特征更接近，异常体的聚焦效果明显提高。

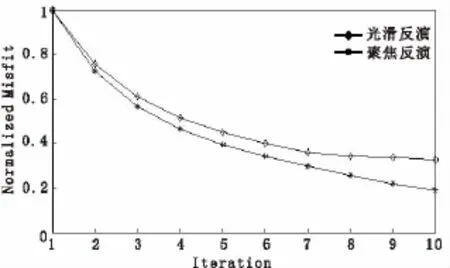
图5 模型一反演归一化拟合差曲线Fig.5 The normalized misfit curves with iteration inversions for model 1

3 结论

作者将最小支撑泛函引入到激发极化数据三维反演的目标函数中，然后采用阻尼型高斯牛顿法求解反演目标函数最优化问题，同时结合预条件共轭梯度法得到激发极化数据三维聚焦反演结果。通过两个模型的试算，算法反演结果增强了异常体成像的聚焦效果，也更好地框定了异常体的范围，反演结果更接近于真实模型。相比较而言，电阻率的反演聚焦效果更明显，极化率的反演无论是光滑反演还是聚焦反演，对异常体的分辨均较好，但对模型的边界位置，尤其是下底边界拟合较差。同时该算法具有计算速度快，占用内存低且易于并行化等优点。

图6 模型二切片图Fig.6 A depth slice of the model 2

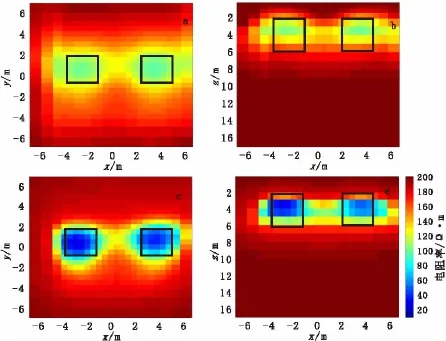
图7 模型二电阻率光滑反演与聚焦反演结果比较Fig.7 Comparisons of focusing inversion with smoothing inversion for model 2

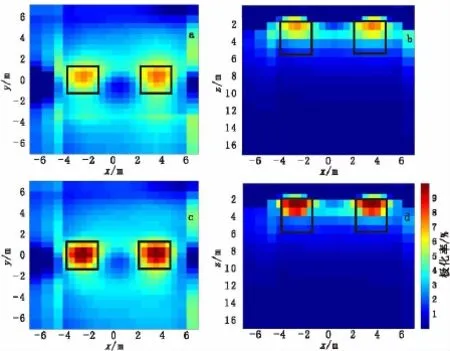
图8 模型二极化率光滑反演与聚焦反演结果比较Fig.8 Comparisons of focusing inversion with smoothing inversion for model 2

［1］ 魏玉山，朱春生，李凯春.激发极化法在金星金矿勘查的应用效果［J］.吉林地质，2010，29（2）：89－93.WEI Y S，ZHU CH S，LIU K CH.The application of induce polarization method in Jinxing gold deposit［J］.Jilin Geology，2010，29（2）：89－93.（In Chinese）

［2］ 王平康，冉波，龙锋，等.激发极化法在内蒙某铅锌矿点成矿预测中的应用［J］.中国矿业，2010，19（7）：108－110.WANG P K，LAN B，LONG F，et al.Application of induce polarization in a lead－zinc deposit metallogenetic prognostication，Inner Mongolia［J］.China Mining Magazine，2010，19（7）：108－110.（In Chinese）

［3］ 陈青松，孙启斌，郭成有.激发极化法在新疆地区找水的应用［J］.西部探矿工程，2002，79（6）：55－57.CHEN Q S，SUN Q B，GUO CH Y.The application of induce polarization in finding water in XinJiang province［J］.West－China Exploration Engineering，2002，79（6）：55－57.（In Chinese）

［4］ 杜炳锐，傅顺，杨威.激发极化法在磨盘山地热勘查中的应用［J］.物探化探计算技术，2010，32（5）：514 －517.DU B R，FU S，YANG W.Application of induce polarization in Mopanshan geothermal resources exploration［J］.Computing Techniques of Geophysical and Geochemical Exploration，2010，32（5）：514－517.（In Chinese）

［5］ BARKER R D.Investigation of groundwater salinity by geophysical methods，in Ward，S.H.，Ed.，Geotechnical and environmental geophysics［J］.Investigations in Geophysics，1990，2（5）：201－211.

［6］ SLATER L D，LESMES D.IP interpretation in environmental investigations［J］.Geophysics，2002，67 （1）：77－88.

［7］ PELTON W H，RIJO L，SWIFT C M.Inversion of two－dimensional resistivity and induced polarization data［J］.Geophysics，1978，43（4）：788－803.

［8］ SASAKI Y.Automatic interpretation of induced polarization data over two－dimensional structures［J］.Memoirs of the Faculty of Engineering，Kyushu University，1982，42（1）：59－74.

［9］ ELLIS R G，OLDENBURG D W.Applied geophysical inversion［J］.Geophysical Journal International，1994，116：5－10.

［10］OLDENBURG D W，LI Y.Inversion of induced po－larization data［J］.Geophysics，1994，59（9）：1327－1341.

［11］LI Y，OLDENBURG D W.3－D Inversion of induced polarization data［J］.Geophysics，2000，65（6）：1931 －1945.

［12］阮百尧，村上裕，徐世浙.电阻率／激发极化率数据的二维反演程序［J］.物探化探计算技术，1999，21（2）：116－125.RUAN B Y，YUTAKA M，XU SH ZH.2Dinversion programs of induced polarization data［J］.Computing Techniques of Geophysical and Geochemical Exploration，1999，21（2）：116－125.（In Chinese）

［13］吴小平.利用共轭梯度方法的激发极化三维快速反演［J］.煤田地质与勘探，2004，32（5）：62－64.WU X P.Rapid 3Dinversion of induced polarization data using conjugate gradient method［J］.Coal Geology ＆Exploration，2004，32（5）：62－64.（In Chinese）

［14］黄俊革.三维电阻率／极化率有限元正演模拟与反演成像［D］.长沙：中南大学，2003.HUANG J G.3Dresistivity／IP modeling and inversion based on FEM［D］.Changsha：Central South University，2003.（In Chinese）

［15］陈进超，王绪本，王丽坤.时间域激发极化法非结构化三角网格有限元正演模拟［J］.物探化探计算技术，2011，33（4）：411－417.CHEN J C，WANG X B，WANG L K.Unstructured triangular grid finite element method for time domain induce polarization forward modeling［J］.Computing Techniques of Geophysical and Geochemical Exploration，2011，33（4）：411－417.（In Chinese）

［16］蒋首进.激发极化二维正反演研究及其在矿产中的应用［D］.成都：成都理工大学，2013.JIANG SH J.To excitation polarization numerical simulation and its application in mineral［D］.Chengdu：Chengdu University of Technology，2013.（In Chinese）

［17］ZHDANOV M S，ELLIS R，MUKHERJEE S.Three －D regularized focusing inversion of gravity gradient tensor data［J］.Geophysics，2004，69：925－937.

［18］SEIGEL H O.Mathematical formulation and type curves for induced polarization［J］.Geophysics，1959，24：547－565.

Regularized focusing inversion of induced polarization data using damped Gauss－Newton method

YE Yi－xin1，2，LI Ze－lin1，FU Chen1，DING Shang－jian1

（1.Fundamental Science on Radioactive Geology and Exploration Technology Laboratory，East China Institute of Technology，Nanchang 330013，China；2.Hubei Subsurface Multi－scale Imaging Lab（SMIL），China University of Geosciences（Wuhan），Wuhan 430074，China）

In this paper，roughness，minimum support functional constraints and reference model，model parameter range constraints are incorporated into the objective function of induced polarization（IP）data inversion.Then we use the damped Gauss－Newton method to find the optimization of the objective function，with the model update being calculated using apreconditioned conjugate gradient algorithm.The method is demonstrated on two synthetic models by comparisons with the results obtained by the traditional inversion method based on smoothness stabilizing functional constraint.The model tests show that the proposed inversion algorithm has good reliability，stability，and high speed.The comparisons show that the program is more convergent and this approach helps to generate more focused and resolved images of blocky geoelectrical structures than traditional inversion approach.

induce polarization（IP）；Gauss－Newton method；focusing inversion；minimum support functional

P 631.3

：A

10.3969／j.issn.1001－1749.2015.06.02

1001－1749（2015）06－0680－07

2014－11－13改回日期：2015－01－07

国家自然科学基金（41204055）；中国地质大学（武汉）地球内部多尺度成像湖北省重点实验室开放基金项目（SMIL－2014－06）

叶益信（1983－），男，博士，主要从事电法、电磁法正反演研究和应用研究工作，E－mail：yixinye321＠126.com。