自抗扰控制技术的原理剖析

代志纲，岳巍澎，隋晓雨，程东霞，张改利

(1. 国网冀北电力有限公司物资分公司，北京 100053；2. 国网新源张家口风光储示范电站有限公司，张家口075000)

自抗扰控制技术的原理剖析

代志纲1，岳巍澎2，隋晓雨2，程东霞2，张改利2

(1. 国网冀北电力有限公司物资分公司，北京 100053；2. 国网新源张家口风光储示范电站有限公司，张家口075000)

本文针对自抗扰控制技术的发展过程及技术核心进行归纳剖析，以单输入单输出系统的自抗扰控制器为基础，对其内部跟踪微分器、扩张状态观测器、非线性误差反馈控制律的结构、功能、特点以及参数整定做了详尽的介绍。同时对单输入双输出系统、双输入单输出系统、双输入双输出系统及多输入多输出系统的自抗扰控制器特点进行剖析，并探讨了未来自抗扰控制研究的方向。

自抗扰控制器；跟踪微分器；扩张状态观测器；参数整定

0 引言

自抗扰控制技术是中科院系统所韩京清研究员于上个世纪九十年代首次提出的一种非线性鲁棒控制技术，是非线性PID控制技术的新发展，它把系统的模型摄动作用当作内扰，将其和系统的外扰一起作为系统总的扰动加以补偿。其思想出发点是PID控制在现有工业控制中占有主导地位，其简单易用并可显示出强大的生命力。但是，针对复杂工业对象，PID控制器不易满足高性能的要求。为了改善PID控制器在强干扰及非线性系统中的控制效果，韩京清在改进非线性PID控制器的基础上提出了自抗扰控制(ADRC)的理念[1，2]。由于自抗扰控制不依赖于被控对象精确的数学模型，算法简单，在未知强非线性和不确定强扰动作用下仍能保证控制精度，使其具有良好的工程应用前景。经过许多不同领域学者进一步的理论分析、数字仿真和部分实验，验证了自抗扰控制对非线性大时滞，环境变化恶劣，强不确定性控制对象的鲁棒性和适应性。如中科院数学与系统所程代展、韩京清、洪奕光、黄一等人先后对机械手、电炉、液压机、空调器、噪音控制、磁悬浮等不同对象模型进行了数值仿真实验，取得了令人满意的效果[3]。北京控制工程研究所的雷仲谋、吕振铎将自抗扰控制应用于航天器姿态控制[4]，清华大学热能工程系孙立明、李东海、姜学智等人将自抗扰控制应用于火电站球磨机制粉系统中，仿真结果也都显示所设计自抗扰控制器在未知强非线性和不确定强扰动作用下能保证良好的控制精度[5]。在电力系统控制中，自抗扰控制理论更是取得较快的发展，中国电力科学院的张采、郭强、周孝信用自抗扰控制理论在电力系统分析综合程序/用户程序接口(PSASP/UPI)平台上为可控串补装置设计了一种新型控制器，仿真结果表明:所设计的控制器不但能快速调节容抗、增加系统阻尼、改善系统稳定性，而且有较强的适应性、鲁棒性，不依赖被控系统的数学模型。经进一步研究得到了可控串补非线性自抗扰控制器的实用方法，并已设计出多机系统的可控串补自抗扰控制器[6,7]。中科院电工所的付旺保,赵栋利将自抗扰控制器用于双馈发电机空载并网控制上，得到一种不需要精确电机参数就可实现并网的控制策略[8]。焦连伟，陈寿孙，王晓丰针对自抗扰控制对于如何具体构造扩张状态观测器尚无明确结论以及还缺乏有实际应用背景的现状，对构造低阶扩张状态观测器给出了一个充分条件，并以直流输电附加控制为背景设计了自抗扰控制器，仿真结果表明所设计的控制器具有良好的控制效果和很强的鲁棒性，可以更好地改善系统的动态特性，显示出这种控制方法在电力系统有着良好的应用前景[9]。清华大学自动化系的高龙等人成功地设计了基于二阶扩张状态观测器(ESO)的ADRC励磁控制方案，并通过短路故障的Matlab仿真验证了自抗扰励磁控制器的有效性，为自抗扰控制理论在发电机励磁控制系统中的应用开了先河[10]。文[11]将微分几何理论和自抗扰控制技术相结合提出了单机无穷大系统的非线性励磁控制规律。清华大学电机系的余涛、沈善德、朱守真，热能系的李东海合作先后将自抗扰控制应用于高压直流输电系统以及汽轮发电机组汽门开度和励磁系统的综合控制[12,13]，仿真证明所提出的基于非线性自抗扰控制的整流侧定电流和逆变侧定熄弧角控制方法具有很强的鲁棒性，适用于较大的模型不确定性和内外扰动；所提出的汽轮发电机汽门和励磁综合控制策略除了具有很好的适应性和鲁棒性外，还能较好地处理汽门和励磁控制的协调性。由以上多个领域的介绍可以看出自抗扰控制理论的应用已取得了一些有益的成果。本文根据被控对象输入输出量的不同，对其进行了分类，并进行了较为详尽的阐述。

1 单输入单输出系统

1.1 组成

自抗扰控制器由非线性跟踪微分器(TD)、扩张状态观测器(ESO)和非线性误差反馈控制律(NLSEF)三部分组成，其结构图如图1所示。

图1 自抗扰控制器结构图Fig. 1 Structure diagram of ADRC

1.1.1 TD

所谓的跟踪微分器是这样的一个机构：对它输入信号ν(t)，它将输出二个信号z1和z2,其中z1跟踪ν(t)，而z2= z1，从而把z2作为ν(t)的“近似微分”。其作用是根据参考输入ν(t)和受控对象的限制来安排过渡过程，得到光滑的输入信号，并提出此过渡过程的各阶导数的动态环节。跟踪微分器的形式有以下几种：

(1)对非线性系统[1]

式中ν为输入信号，0 ＜ α ＜ 1, δ ＞ 0。而函数则为

式中，r表示跟踪微分器的快慢因子。r越大，跟踪效果越好，即z1(t)越接近ν(t), z2(t)越接近ν(t)的导数或广义导数。反之则差。β是表示跟踪快慢的微调因子，同时也控制跟踪信号z1和z2有无超调和超调大小。

式中r是跟踪微分器的快慢因子，而δ ＞ 0表示线性区间的大小[1]。函数为

(3) TD的离散形式[14]

z11跟踪ν(t)，z12收敛于ν(t)的导数。r和h为可调参数，r越大跟踪速度越快，h越大，滤波效果越好，但r和h又是一对矛盾，两者需协调配合[14]。

对于某一频率或频率变化较小的情况下，非线性跟踪微分器对输入信号及其一阶微分具有较好的跟踪效果，但当频率范围变化较大时，其跟踪性能相对于线性跟踪微分器来说没有大的改善。

完整的二阶ADRC中有跟踪微分器TD这一环节，其作用是安排理想的过渡过程并给出过渡过程的微分信号。但考虑到时滞对象本身就反应迟缓，故考虑去掉TD,希望能借助一开始的大误差控制信号把对象“激励”起来，让输出尽快冲出去。此外,对于恒值控制系统,也可省去TD[ 15]。

1.1.2 ESO

扩张状态观测器是自抗扰控制器的核心环节。控制器仅需要系统的输入量和输出量作为信息来源，通过扩张状态观测器不仅可以得到各个状态变量的估计，而且能够估计出不确定模型和外扰的实时作用量，以使对象的不确定性在反馈中加以补偿，从而达到重新构造对象的目的。

设有未知外扰作用的不确定对象

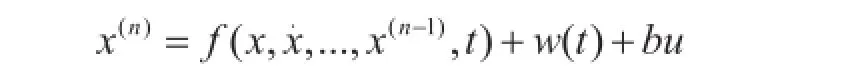
则z2n+1是对总扰动的实时估计，b0为b的估计值，非线性函数一般选择为式(2)的形式。

扩张状态观测器对被观测系统的输出状态有较好的跟踪能力，其动态品质主要取决于增益b，且响应越快，估计的精度越高，但对总扰动的实时估计受到某些条件的限制。例如，当外扰频率较高时，扩展状态观测器对总扰动跟踪能力较差。

1.1.3 NLSEF

非线性状态误差反馈控制律是跟踪微分器和扩展状态观测器产生的状态变量估计之间的误差的非线性组合，它与扩张状态观测器对总扰动的补偿量一起组成控制量。

根据fal函数的特点和现场运行经验，适当地选择非线性因子α，将极大地改变控制效果，使比例、微分各自发挥出各自的功效。对于比例作用，在小误差时应采用大增益,大误差时应采用小增益，故取fal()中的α为-1＜α＜0。对于微分作用，在微分误差小时应采用小增益，微分误差大时应采用大增益，故取fal()中的α为α＞1。

综上所述，自抗扰控制器是对“反馈系统中的线性与非线性”，“模型论与控制论”等一系列根本问题进行不懈探索的结果。利用自抗扰控制器进行系统设计时，可以把系统中的许多不同因素归类为对系统的扰动，然后用扩张状态观测器进行估计补偿，使其变为线性系统标准型——积分串联型，从而实现动态反馈线性化。

1.2 参数整定

ADRC的三个主要部分TD、ESO、NLSEF是相互独立设计的，或者说是用“分离性原理”设计的。因此，在进行参数整定时，也可相互独立地进行。

ADRC的参数比较多，但一般而言，非线性参数(以二阶ADRC为例)如ESO的及NLSEF的都可根据实际运行经验取为固定值[16]。如 α01=1, α02=0.5, α03=0.25, α1=1/0.75, α2=1/1.5。取上述值时，都不会用到幂函数，只需用到平方根函数，实现起来非常方便。δ0，δ的选取对ADRC的性能也有较大的影响，如果δ0，δ选的较大，ADRC可能只工作在线性区，如果δ，δ0选的太小，ADRC又可能出现振颤现象，故它们的选择应根据现场的实际情况决定。

1.2.1 TD和NLSEF参数整定

为了保证TD有足够快的跟踪速度，频带设置较宽。TD 的传递函数为

1.2.2 ESO参数整定

ESO采用三阶线性结构,其状态方程为

受控对象改造为

式(9)和(10)相减得

1.2.3 遗传算法参数寻优

自抗扰控制器需调整的参数众多，由于目前还缺乏相关的成熟理论，使得整定过程和效果在很大程度上依赖于人的经验。文献[17]提出了基于遗传算法的ADRC参数自整定及优化的方法，遗传算法的基本思想是把待优化问题的参数进行编码，然后由若干个编码后的个体形成一个初始群体作为待求问题的候选解，使用选择、交叉和变异三种算子进行操作，不断迭代优化，直到满足终止条件。由于采用了参数的大范围搜索策略，势必会产生大量的不可行染色体，必须引入适当的策略，使算法能迅速自动识别并跨越不可行染色体。为此，系统的输出y在ν1附近设定一个可行区间，使系统输出落在该可行区间的染色体为可行解，算法进行适应度的评估并进行遗传算子的操作；反之，算子拒绝染色体的适应度评估，直接给出一个较大的惩罚值P。仿真表明加入惩罚策略的浮点遗传优化算法能高效地完成控制器众多参数的大范围寻优，摆脱了ADRC控制器参数整定和优化对经验的依赖，具有广泛的应用价值。

1.2.4 参数整定的单纯形法

长期以来，自抗扰控制器参数的整定一直采用试凑的方法，文献[18]提出应用单纯形法进行自抗扰控制器参数的整定。用积分来表达闭环系统的性能指标，问题就变成选择ADRC的参数使指标J达到极小。这里采用单纯形法对其进行优化，使它们满足:，首先由人工整定出一组ADRC参数，用它作为单纯形法优化的初始点。然后再选择一个初始步长就可以用单纯形法进行优化。采用这种方法对常见被控对象的ADRC参数组进行优化，可以得到比较满意的结果。特别在整定ADRC中的扩张状态观测器时，在人工整定很难改进的情况下，用它可以得到较好的结果。

一般情况下，对由ADRC组成的闭环系统其位置误差比速度误差小一个数量级，而速度误差又比加速度误差小一个数量级。为进一步改进优化结果和提高优化效率，可对优化目标引入恰当的非线性函数。仅对标称被控对象优化的控制器，往往没有对对象参数变化的适应性以及控制器对自身参数变化的鲁棒性。通过将优化目标由单个标称对象变为对象参数变化的两极，使整定出来的控制器不再是针对一个对象的，而是一个对象类的控制器，这样的控制器自然就具备了对对象参数变化的适应性和控制器自身参数变化的鲁棒性。事实上，只要对象结构和参数变化使得闭环系统时间尺度没有明显的变小，该控制器都将能适应对象的这种变化。这种控制器参数整定方法为设计对一个对象类进行控制时，具有上述性质的控制器设计提供了一种途径。

1.3 时间尺度

在自抗扰控制器中使用时间尺度作为衡量系统反应快慢的一个标准。它类似于线性控制系统的时间常数。它的作用在于：对于时间尺度为T的对象调整好的具有一定鲁棒性的ADRC,只需通过时间变换，就可直接用于时间尺度为的对象，且ADRC仍具有同样的鲁棒性。

从另一角度而言，时间尺度提供了一种控制器“快速学习、快速适应”对象性能变化的有效方法。实际上，每个对象都有一个时间尺度(时间常数)，将该尺度相对于标准对象的标准控制器参数做时间尺度变换后，即可直接用于该对象的控制。当然有时需要在此基础上微调控制器参数，以获得良好的控制效果，但即便如此，也比在完全未知的情况下去调整控制器参数要快速有效的多。

对时间尺度为p1的闭环系统整定好了ADRC参数。只要b01和b相差不大且关系式成立，那么控制时间尺度为p的闭环系统达到闭环性能要求的ADRC参数将由(13)式确定[18]。

可以看出，从控制的角度看，控制器设计所需对象信息，不再是对象模型中的f (x1,x2)是什么函数，而是其在实现控制过程中的变化快慢，也就是闭环系统时间尺度的大小而不是对象线性或非线性的特性。因为不管线性还是非线性对象，它们的时间尺度在实现某一控制过程中很可能是相同的。从控制器时间尺度变换公式(13)可以看出，控制器参数整定所需要的闭环时间尺度不仅依赖于对象的快慢特性，也依赖于控制器对闭环系统所要求的性能指标。它将控制器参数的调整与对象快慢特性和闭环性能指标联系了起来。

1.4 跨阶控制

自抗扰控制器(ADRC)是有阶数的，即如果对象为N阶，就要用N阶ADRC来控制。二阶ADRC因其结构简单，参数易整定等优点而应用最为广泛。用二阶ADRC控制二阶对象时，有一套标准参数。即在整定任何二阶控制对象时，均可由该套参数出发。文献[19]提出了用二阶ADRC控制一阶和三阶对象的理念，并阐述了调参依据和两套标准参数。仿真表明，两种情况下该套参数的控制效果都很理想，表现出很强的鲁棒性和适应性。文献[20]对ADRC在高阶系统中的应用进行了探讨，以理论分析为基础，将其基础部件――跟踪微分器TD和扩张状态观测器ESO的设计予以简化和改进。TD除了跟踪参考输入信号r(t)，安排预期动力学特性外，其主要作用还在于柔化r(t)的变化，以减少控制过程输出的超调量。而在实际工程应用中，往往只需要构造满意的预期动力学特性，勿需最优，因此TD可用某些结构简单的柔化环节来实现。例如，当被控对象的惯性或延迟较大时，可将TD设计为线性惯性环节。而高阶ESO可用几个参数完全相同的低阶状态观测器串联来实现，可大大减少需整定的参数个数，降低整定难度[21]。

2 单输入双输出系统

通常的自抗扰控制技术处理的对象是单输入单输出系统，而倒立摆系统由摆的偏角和小台车位移两个二阶系统构成，它们受同一个电机的输出电压的控制，两个系统相互耦合。倒立摆系统控制的关键是对摆的偏角的控制，因此控制律设计必须以摆的偏角的控制为主，同时兼顾对小台车的位移控制。倒立摆系统的数学模型为

如果把x4当作外扰，对摆的偏角的控制完全可以按典型的自抗扰控制技术来设计控制律，但一般不能保证小台车的位移能够满足控制目标。对于这样的单输入双输出、强非线性、强耦合的不稳定系统，在原自抗扰控制算法的基础上，增加一个跟踪微分器，将控制律写成两个输入量与设定值的误差和其微分的组合形式，通过调节它们的增益系数来达到控制的目的[22]，突破了原有的自抗扰控制算法只适应于单输入单输出系统的限制，实现了摆的偏角和小台车位移的良好控制效果，仿真证实了该方法的有效性。

3 双输入单输出系统

文献[23]以电压型PWM逆变器为例介绍了一个双输入单输出系统的自抗扰控制策略。单相全桥正弦波逆变电源系统的状态方程如下：

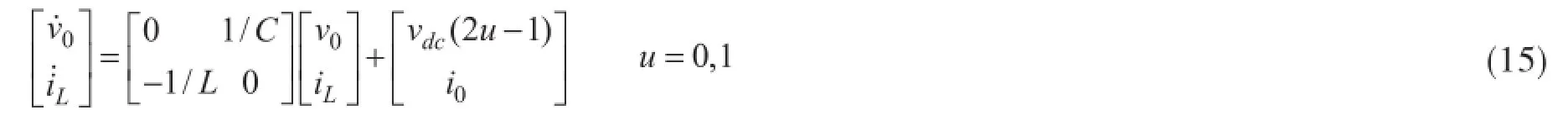
得到的逆变电路模型是一个双输入、单输出二阶系统，两个输入量分别是输入电压Udc和负载电流i0，u体现了控制作用，i0视为扰动。对于任一输入量，输出电压ν0都是可控的。根据逆变器的数学模型可以设计自抗扰控制器，自抗扰控制器只需检测输入和输出电压，以任意给定的ν0*为ADRC的参考输出，u为控制输入量，控制的目的是要达到使系统输出ν0能跟踪给定值ν0*。

4 双输入双输出系统

文献[24]介绍了双输入双输出系统的解耦控制方法。

设有被控对象

式中，f1，f2均为不确定函数，w1(t), w2(t)为未知外扰。令

在此假定矩阵B(t)在某一域中可逆。如果矩阵B(t)已知，那么U1和U2分别把

当作各自的系统“扰动”而实现自抗扰控制，这样就能实现解耦控制。如果矩阵B(t)不确定，在B(t)的变化范围内取一可逆矩阵B0，并把当作系统的新的“外扰”项。若矩阵不甚大，那么就能用U1和U2分别实现各自通道的自抗扰控制，从而最终也实现解耦控制。文献[25]运用该方法实现了发电机组的同期并网控制.

5 多输入多输出系统

随着控制理论的发展，控制对象越来越复杂，多输入多输出系统日益成为研究的热点，通过解耦可将多输入多输出MIMO系统转化为多个单输入单输出系统SISO。文献[26，27]利用多个SISO自抗扰控制器实现了MIMO对象的综合控制，但由于自抗扰控制器参数整定的复杂性，多个SISO自抗扰控制器之间的协调率往往无法确定因而很难对整个MIMO系统的闭环稳定性给出一个满意的数学解释。

文献[28]首次把ADRC方法拓展到多输入多输出非线性对象协调控制的研究中，文献[29]提出了内环用ESO反馈线性化，外环根据线性H原理和协调律进行预期动力学特性选取的设计方法，可实现观测器和线性化的有机结合，并进行了相应的稳定性分析，为ADRC用在多变量协调控制提供了新思路。经过对内环反馈线性化处理后，外环已经被线性化为一个伪线性系统，从而可以直接运用线性控制理论进行协调控制器的设计。

6 总结

综上所述，我们可以得到自抗扰控制技术的重要结论：

(1)自抗扰控制器是对PID的改进，省去了积分环节，增加了扩张状态观测器以实现对系统内部模型摄动和外部扰动的实时估计，并采用非线性误差状态反馈策略，保留了PID控制器的优点，克服了其控制精度低的缺陷。

(2)自抗扰控制器的构成并非一成不变，需根据实际对象的特征灵活设置。

(3)自抗扰控制器的参数整定是当前研究的热点，除了上述的遗传算法参数寻优、参数整定的单纯形法外，神经元自学习方法、基于神经网络的参数整定法也被广泛研究，但尚未有一种被广为接受的系统的方法。

(4)多输入多输出系统的变量通常相互关联，可将多输入多输出系统解耦使其转化为多个单输入单输出系统，然后利用现有的控制理论对各个单输入单输出系统进行控制。但对于跟踪系统而言，可直接设计自抗扰控制器使得系统的一路输出跟踪一路输入，将耦合作用当作一种内部扰动处理，加以补偿，这样各个输出之间不再关联而只与其跟踪的输入有关，复杂的非线性多变量系统解耦完毕。

(5)自抗扰控制器已经在多个领域的应用取得了一些有益的成果，但大多数成果仍处于仿真或简单的实体实验阶段，并且集中于低阶系统模型的应用，对高阶系统自抗扰控制器的阶数确定，扩张状态观测器的稳定性证明，控制参数的整定与优化等方面还缺乏深入的研究，许多工作有待于进一步展开。

[1] 韩京清. 从PID技术到“自抗扰控制”技术[J]. 控制工程, 2002, 9(3): 13-18.

Han J Q. From PID Technique to Active Disturbances Rejection Control Technique[J]. Control Engineering of China, 2002, 9(3): 13-18.

[2] 黄一, 张文革. 自抗扰控制器的发展[J]. 控制理论与应用, 2002, 19(4): 485-491.

Huang Y, Zhang W G. Development of Active Disturbance Rejection Controller [J].Control Theory and Applications, 2002, 1(4): 485-491.

[3] 韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19-23.

Han J Q. Auto-disturbances-rejection Controller and It's Applications[J]. Control and Decision, 1998, 13(1): 19-23

[4] 雷仲谋, 吕振铎. 非线性自抗扰控制器在航天器姿态控制系统中的应用[J]. 航天控制, 2000, 18(4): 34-39.

Lei Z M, Lu Z D. Nonlinear Auto-Disturbance Rejection Controller for Spacecraft Attitude Control System [J]. Aerospace Control, 2000, 18(4): 34-39.

[5] 孙立明, 李东海, 姜学智. 火电站球磨机制粉系统的自抗扰控制[J]. 清华大学学报(自然科学版), 2003, 43(6): 17-18.

Sun L M, Li D H, Jiang X Z. Automatic Disturbance Rejection Control for Power Plant Ball Mill [J]. Journal of Tsinghua University (Science and Technology), 2003,43(6): 17-18.

[6] 张采, 周孝信. 可控串补自抗扰控制器[J]. 电网技术, 1997,21(5): 56-61.

Zhang C, Zhou X X. Auto-Disturbance Rejection Controller for Thyristor Controlled Series Capacitor [J]. Power System Technology, 1997, 21(5): 56-61.

[7] 郭强, 周孝信. 可控串补非线性自抗扰控制的参数优化[J]. 电网技术, 1999, 23(11): 28-30.

Guo Q, Zhou XX. Parameter Optimization of Auto-Disturbance Rejection Controller of Thyristor Controlled Series Capacitor [J]. Power System Technology, 1999, 23(11): 28-30.

[8] 付旺保, 赵栋利, 潘磊等. 基于自抗扰控制器的变速恒频风力发电并网控制[J]. 中国电机工程学报, 2006, 26(3): 13-18.

Fu W B, Zhao DL, Pan L. Cutting-in Control of the VSCF Wind-power Generator Based on Auto-disturbance Rejection Controller [J]. Proceedings of the CSEE, 2006, 26(3): 13-18.

[9] 焦连伟, 陈寿孙, 王晓丰. 电力系统自抗扰控制器[J]. 清华大学学报(自然科学版), 1999, 39(3):8-9,34.

Jiao L W, Chen S S, Wang X F. Power System NLSEF Controller [J]. Journal of Tsinghua University(Science and Technology), 1999, 39(3): 8-9, 34.

[10] 高龙, 韩俊生, 李崇坚等. 非线性鲁棒自抗扰控制器在电力系统中的应用[J]. 清华大学学报(自然科学版), 2000, 40(3): 16-31, 32.

Gao L, Han J S, Li C J. Nonlinear Robust Auto-Disturbance Rejection Controller for Power Systems[J]. Journal of Tsinghua University (Science and Technology), 2000, 40(3):16-31,32.

[11] 马幼捷, 王新志, 周雪松. 基于微分几何理论和自抗扰控制技术的励磁控制器设计[J]. 电工电能新技术, 2007, 26(1): 34-37.

Ma Y J, Wang X Z, Zhou X S. Excitation Control Design Based on Differential Geometry Theory and Active Disturbance Rejection Control[J]. Advanced Technology of Electrical Engineering and Energy , 2007, 26(1): 34-37.

[12] 余涛, 沈善德, 李东海. 高压直流输电系统的自抗扰控制方法[J]. 电力系统自动化, 2002, 26(22): 22-26.

Yu T, Shen S D, Li D H. Study on Auto-Disturbance Rejection Control for HVDC System [J]. Automation of Electric Power Systems, 2002, 26(22): 22-26.

[13] 余涛, 沈善德, 李东海等. 汽轮发电机组汽门开度和励磁系统的自抗扰综合控制[J]. 电力系统自动化, 2003, 27(3):36-41.

Yu T, Shen S D, Li D H. Nonlinear Coordinated Auto-Disturbance Rejection Governor and Excitation Controller for Synchronous Generators[J]. Automation of Electric Power Systems , 2003, 27(3): 36-41.

[14] 陈慧琴. 基于自抗扰控制器的永磁同步电动机交流调速系统的研究[D]. 天津: 天津大学, 2004.

Chen H Q. Research on Permanent Magnet Synchronous Motor AC Drive System Based on ADRC [D]. Tianjin: Tianjin University, 2004.

[15] 刘翔, 姜学智, 李东海. 水轮发电机组调速系统的自抗扰控制[J]. 清华大学学报(自然科学版), 2001, 41(10): 69-73.

Liu X, Jiang X Z ,Li D H. Auto Disturbance Rejection Control for Hydro Turbine Governor [J]. Journal of Tsinghua University (Science and Technology), 2001, 41(10): 69-73.

[16] 要晓梅. 自抗扰控制器的应用扩展研究[D]. 北京: 北京理工大学, 2002.

Yao X M. Research on extended applications of Auto disturbance Rejection Controller [D]. Beijing: Beijing University of Tecnology, 2002.

[17] 李海生, 朱学峰. 自抗扰控制器参数整定与优化方法研究[J]. 控制工程, 2004, 11(5): 419-423.

Li H S, Zhu X F. On Parameters Tuning and Optimization of Active Disturbance Rejection Controller[J]. Control Engineering of China, 2004, 11(5): 419-423.

[18] 张文革. 时间尺度与自抗扰控制器[D]. 北京: 中国科学院系统科学研究所, 1999.

Zhang W G. Time Scale and Active Disturbance Rejection Controller[D]. Beijing: Institute of Systems Science, Chinese Academy of Sciences, 1999.

[19] 要晓梅, 王庆林, 刘文丽等. 一般工业对象的二阶自抗扰控制[J]. 控制工程, 2002, 9(5): 59-62.

Yao X M, Wang Q L, Liu W L. Two-order ADRC Control for General Industrial Plants [J]. Control Engineering of China, 2002, 9(5): 59-62.

[20] 刘翔, 李东海, 姜学智, 等. 自抗扰控制器在高阶系统中应用的仿真[J]. 清华大学学报(自然科学版), 2001, 41(6): 95-99.

Liu X, Li D H, Jiang X Z, etal. Simulation Study of Active Disturbance Rejection Controller for High-order Systems[J]. Journal of Tsinghua University (Science and Technology), 2001, 41(6): 95-99.

[21] 张荣. 提高自抗扰控制器性能的探讨[D]. 北京: 中国科学院系统科学研究所, 1998

Zhang R. Discussion on performance improvement of ADRC[D]. Beijing: Institute of Systems Science, Chinese Academy of Sciences, 1998

[22] 武利强, 韩京清. 直线型倒立摆的自抗扰控制设计方案[J]. 控制理论与应用, 2004, 21(5): 665-669.

Wu L Q, Han J Q. Active Disturbance Rejection Controller Scheme for the Linear Inverted Pendulum [J]. Control Theory and Applications, 2004, 21(5): 665-669.

[23] 邹祖冰,蔡丽娟,甘辉霞. 电压型PWM逆变器的自抗扰控制策略[J]. 电工技术学报, 2004, 19(2): 84-88.

Zou Z B, Cai L J, Gan H X. The Application of Auto-Disturbance Rejection Controller for Voltage Source PWM Inverter [J]. Transactions of China Electrotechnical Society, 2004, 19(2): 84-88.

[24] 韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19-23.

Han J Q. Auto-disturbances-rejection Controller and It's Applications[J]. Control and decision, 1998, 13(1): 19-23.

[25] 王春山, 孙秀霞, 吴剑. 自抗扰控制器及其在发电机组同期并网控制中的应用研究[J]. 现代电子技术, 2003, 27(2): 61-63.

Wang C S, Sun X Q, Wu J. Auto-disturbances-rejection Controller and it's Application in Fast Following Synchronizer of Generators [J]. Modern Electronic Technique, 2003, 27(2): 61-63.

[26] 冯光, 黄立培, 朱东起. 异步电机的新型非线性自抗扰控制器的研究[J]. 清华大学学报(自然科学版), 1999, 39(3): 30-33.

Feng G, Huang L P, Zhu D Q. Nonlinear control algorithm for induction motors[J]. Journal of Tsinghua University (Science and Technology), 1999, 39(3): 30-33.

[27] 冯森林, 李勇朝, 刘淑华, 等. 多用户MIMO 系统中非均匀码本的构建[J]. 新型工业化, 2013, 3(11): 60-69

Feng Senlin, Li Yongzhao, Liu Shuhua, et al. Construction of uneven codebook in multi-user MIMO system[J]. The Journal of New Industrialization, 2013, 3(11): 60-69

[28] 陈夕松, 杨俊, 郭聪, 等. 基于干扰观测器的模型预测控制实验研究[J]. 新型工业化, 2011, 1(6): 15-21.

Chen Xisong, Yang Jun, Guo Cong, et al. Disturbance Observer Enhanced Model Predictive Control With Experimental Studies#[J]. The Journal of New Industrialization, 2011, 1(6): 15-21.

[29] 余涛, 沈善德, 李东海, 等. 静止移相器和发电机励磁系统的自抗扰协调控制[J]. 中国电机工程学报, 2003, 23(9): 1-5.

Yu T, Shen S D, Li D H. Coordinated Auto Disturbance Rejection Control of Static Phase Shifter and Excitation System [J]. Proceedings of the CSEE, 2003, 23(9): 1-5.

Dissection on the Principle of Active Disturbance Rejection Control Technology

DAI Zhigang1, YUE Weipeng2, SUI Xiaoyu2, CHENG Dongxia2, ZHANG Gaili2
(1. State Grid Jibei Electric Power Co. Ltd. Material Branch, BeiJing 100053, China; 2. State Grid Xin Yuan Zhangjiakou Scenery Storage Demonstration Power Plant Co. Ltd., Zhangjiakou 075000, China)

This paper concludes the development process of auto disturbance rejection control technology and core technology. Based on the single input single output system with ADRC, the structure, function, characteristics and parameters tuning of tracking differentiator & expanded state observe will be detailed introduction. At the same time for a single input double input and double output system, single output system, double input and double output system and multi input multi output system with ADRC characteristics are analyzed, and discussed the future direction of auto disturbance rejection control research.

Active Disturbance Rejection Control (ADRC); Tracking Differentiator (TD); Expanded State Observe (ESO); Parameters tuning

10.3969/j.issn.2095-6649.2015.01.08

国网新源张家口风光储示范电站有限公司科技项目(FGC-FW(II))

代志纲(1970-), 男, 硕士, 工程师, 主要研究方向: 新能源并网与控制; 岳巍澎(1986-), 男, 工程师, 主要研究方向:新能源发电与控制; 隋晓雨(1988-), 男, 助理工程师, 主要研究方向: 新能源发电与控制; 程东霞(1985-), 男, 助理工程师, 主要研究方向: 新能源发电与控制; 张改利(1986-), 男, 助理工程师, 主要研究方向: 新能源发电与控制

代志纲，岳巍澎，隋晓雨，等．自抗扰控制技术的原理剖析[J]．新型工业化，2015，5(1)：49-58